MOJ
eISSN: 2572-8520


Review Article Volume 3 Issue 5
Department of Civil Engineering, Aristotle University of Thessaloniki, Greece
Correspondence: Sotiria P Stefanidou, Postdoctoral Researcher, Department of Civil Engineering, Aristotle University of Thessaloniki, Greece
Received: August 24, 2017 | Published: November 20, 2017
Citation: Stefanidou SP. Software for bridge-specific fragility analysis. MOJ Civil Eng. 2017;3(5):351-357. DOI: 10.15406/mojce.2017.03.00081
Bridges within a road network have different geometries, structural systems and member properties, mainly due to differences in the site topography and the construction method selected; therefore, the use of the same seismic fragility functions for all bridges of a certain class, neglecting the specific characteristics of their key components and of the seismic demand (that also varies with the site) is in principle inconsistent, albeit commonly done in loss assessment projects. To gain more insight into this, this paper focuses on the software development for the application of a recently proposed methodology and the derivation of bridge-specific fragility curves. Using the fully parameterized ad-hoc software, component-specific threshold values are calculated, whereas bridge system analysis is performed for the estimation of demand at component control point and the calculation of component and system fragility curves. Uncertainty in seismic capacity and demand are additionally calculated. All input data necessary for bridge-specific fragility analysis are discussed and the application of the software for the assessment of a bridge inventory is presented.
Keywords: bridges, seismic assessment, fragility curves, reinforced concrete
Damage due to earthquake is commonly related to substantial direct and indirect losses, highlighting the need for damage detection and retrofit prioritization based on the results of the seismic risk assessment of the road network. In this context, numerous methodologies have been developed for the seismic vulnerability assessment of bridges for different levels of seismic hazard using fragility curves; analytical.1–3 as well as empirical.4 procedures have been put forward. In most cases, bridges within a road network have different structural and geometric properties depending on the site topography, the selected structural system and construction method, and the foundation soil. In the literature,13,5–7 bridges are classified into different categories, while, under the assumption that the seismic performance of bridges within the same class is similar, fragility curves of the representative -of each category-bridge are typically used for the seismic assessment of the bridge stock. The number of spans, number of columns (single or multicolumn bents), skewness, deck type, pier type and the pier-to-deck connection, are some of the parameters considered in classification schemes available in the literature.1,3,5,6 The effect of geometry (i.e. total deck length and width, pier height) on bridge fragility is fully recognized,1,8 therefore different bridge geometries within the same category were studied in order to highlight the differences compared to the representative bridge. 2,8 The importance of bridge-specific fragility curves in the seismic assessment of road networks is presented in,9 highlighting the differences (lower and upper level) in fragility of bridges within the same category, compared to the representative bridge.
The estimation of bridge-specific fragility curves is a rather demanding procedure since the seismic performance of critical bridge components is related to the individual bridge structural system configuration. Therefore, assessment of the case study bridge is necessary in order to provide bridge-specific fragility curves. In the context of the above, the main objective of this paper is to develop and describe an ad-hoc software for the application of a new, recently proposed,10 methodology for bridge-specific fragility analysis. The software is fully parametrised and requires the completion of several forms in order to calculate component capacity (based on single component analysis), component demand (based on system analysis) and relevant uncertainties. Based on structure-specific properties (namely geometric properties, deck type, pier type and the pier -to-deck connection, etc.) the structural model is developed and analysed using OpenSees platform (open source software).11 The software has a wide application to different bridge inventories, since a wide range of different bridge types is supported. Application to bridges of Egnatia motorway (Western Macedonia section) is presented herein.
The component-based methodology for the derivation of bridge-specific fragility curves for a concrete bridge stock using the ad-hoc developed software is described in detail in.10 The main aspects of the proposed methodology are the case-specific definition of component capacity and threshold limit state values for the quantification of damage considering the effect of different component properties, failure modes and boundary conditions, as well as the elastic analysis of a simplified model for the estimation of demand at component level, and, finally, the uncertainty treatment. Critical components for the system’s seismic performance, namely bridge piers, abutments and bearings (Figure 1) are considered. Therefore, capacity is defined at component level, accounting for the effect of different geometric, material, loading and member detailing parameters on component strength and ductility and, eventually, damage threshold value. As described in,10 global engineering demand parameters (EDPs) are used for the quantification of component damage, accounting for different failure modes and boundary conditions. However, local to global demand parameter mapping is performed in order to describe global damage in qualitative terms. On the basis of the above, limit state (damage) thresholds for the various limit states considered in fragility analysis are defined for each critical component in terms of the displacement of the control point, as shown in Table 1.
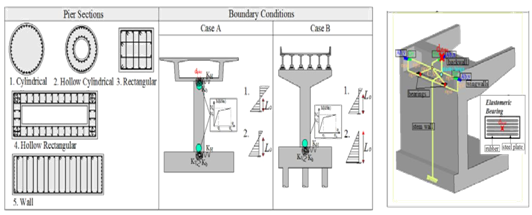
Figure 1 Critical bridge components-Pier types considered in the database and different boundary conditions.
|
Limit State |
R/C piers/EDP: d(m) |
Abutments EDP: d(m) |
Bearings EDP: |
|
|
Local |
Global |
|||
|
LS 1-Minor/slight damage |
φ1:φy |
d1:min{d(φ1)d(V1)} |
d1=1.1.dgap (μφ,backwal=1.5) |
20 (d1=0.02.hbr) |
|
LS 2-Moderate/ damage |
φ2:min (φ: εc>0.004,φs)≥0.015) |
d2:min{d(φ2)d(V2)} |
d3=0.035.hbackwalll |
100 (d2=0.1.hbr) |
|
LS 3-Major/Extensive damage |
φ2:min (φ: εc≤0.004+1.4.ρw.fywfcc,φ:εs≥0.16) |
d3:min{d(φ3)d(V3)} |
d3=0.035.hbackwalll |
200 (d3=0.2.hbr) |
|
LS 4-Failuer/Collapse |
φ4:min (φ: M<0.90.Mmax, φ:εs≥0.075) |
d4:min{d(φ4)d(V4)} |
d4=0.1.hbackwalll |
300 (d4=0.3.hbr) |
Table 1 Limit state thresholds for critical structural components.
Regarding bridge piers, damage is initially defined at section level, using local demand parameters (section curvature), related to experimentally estimated damage (e.g. crack widths), while threshold limit state values are expressed at component level in terms of a global demand parameter, based on the results of pushover analysis, as described in.10 Based on multiple parametric analyses and regression analysis of results, empirical relationships (having the form of Eq. (1)) are proposed for the estimation of limit state thresholds in global terms, accounting for the effects of different section types, as well as geometric, material, loading and reinforcement parameters on component capacity and threshold limit state values. Threshold values calculated using Eq. (1) refer to the equivalent cantilever (Lo); the level of the contraflexure point should be defined (pier top to bottom moment ratio) in order to relate them to threshold values of the restrained pier, as described in.9,10
(1)
For the quantification of abutment and bearing damage, threshold limit state values are defined in terms of displacement of the component control point, based on experimental results and other information from the literature, as described in.10 In particular, threshold displacement values for abutments are related to the gap size and backwall height, while threshold displacement values for elastomeric bearings are related to shear strain (Table 1). Component capacity and limit state thresholds are defined accounting for the bridge-specific parameters and properties; moreover, uncertainty in capacity (βc) and limit state definition (βLS) should also be considered; the latter depend on component type and the selected demand parameter, and are quantified in,9 and.10
Software development for bridge-specific fragility analysis
The Matlab-based software developed for the implementation of the previously described methodology and the derivation of bridge-specific fragility curves has three parts; component capacity is estimated within Part 1, component demand within Part 2, while uncertainties (in capacity and demand) and fragility curves are calculated within Part 3. In particular, component-specific limit state thresholds are calculated using the ad-hoc developed, Matlab-based software (Part 1). The user should provide geometric, material and loading information; section analysis is automatically performed in order to define threshold values in local terms and pushover analysis of bridge pier is subsequently performed in order to define threshold values in global terms. It should be underlined that both section and pushover analyses are performed using freely distributable software (AnySection,12 and OpenSees respectively), therefore they should be downloaded and installed by the user. Despite the fact that component analysis and estimation of threshold value is not time consuming, the user could alternatively use empirical equations presented above (Eq.1), which are incorporated in the software. The latter is proposed for the cases that the parameters of equation 1 are unknown and their values should be based on assumptions. The calculation of component demand, based on bridge system analysis results, is illustrated in Figure 2. The software is based on a generic simplified 3d bridge model created using the OpenSees platform.11 Input data provided by the user are depicted in Figure 2 and concern general bridge geometry and loading properties, component (pier, bearing, and abutment) properties, and the (site-specific) response spectrum. Threshold limit state values for piers are automatically calculated in displacement terms according to the geometric, material, reinforcement, loading properties and boundary conditions in each case based on empirical relationships (or calculated in Part 1 as described above). Dispersion values, calculated in line with the procedure described in,9 are also included. Seismic demand is calculated at component level based on response spectrum analysis results for various IM levels , while the evolution of damage with earthquake intensity is plotted for every component considered. Different boundary conditions at abutments are considered for the case of open and closed gap, whereas fragility curves are automatically calculated for longitudinal and transverse directions separately (Part 3), under the assumption of series connection between components (lower bound). As already mentioned, the software developed is based on a generic simplified 3d bridge model, fully parameterized, applicable to a wide range of different bridge types. The distinct steps for the development of bridge model, the calculation of component demand and the estimation of fragility curves, are summarized in Figures 3-5.
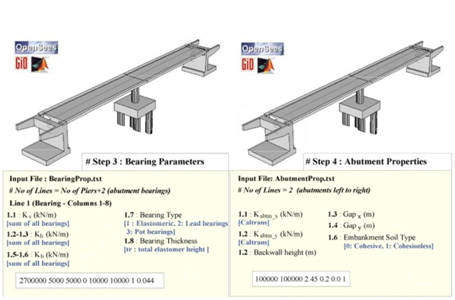
Figure 5 Software for bridge-specific fragility analysis: Step 3–Bearing and abutment input Application to bridge inventory (Egnatia Motorway). Different bridge classes in Egnatia Motorway, Western Macedonia section.
General geometry, loading and structural system properties are defined at step 1, in order to form the bridge model and perform elastic analysis for the estimation of component demand at control points. Component properties are defined in Steps 2, 3 and 4 for piers, bearings and abutments respectively, in order to form the structural model and define component capacity (limit state thresholds). The methodology described in §2 is applied to all bridges of an Egnatia Motorway section (Western Macedonia, Greece), a total of 44. Bridge-specific fragility curves are calculated for each bridge (for the longitudinal and transverse direction separately) and the results are discussed, highlighting the importance of the bridge-specific approach in assessing a bridge inventory. The bridges of the inventory are initially classified into categories according to the classification scheme presented in,3 and summarised in Table 2. A code number is defined for each bridge according to the pier, deck and the pier-to-deck connection type.
Code number |
X1 |
X2 |
X3 |
Pier type |
Deck type |
||
Description |
Description |
Description |
|
1 |
Single column - |
Slab (solid or with voids) |
Monolithic |
2 |
Cylindrical section Single |
Box girder |
Through bearings |
3 |
Multi-column bent |
Simply supported precast-prestressed |
Combination of monolithic and bearing |
4 |
Wall-type |
beams |
connections |
5 |
V-type |
- |
- |
Table 2 Classification scheme for bridges in a road network
All different bridge classes of the studied section of Egnatia Motorway are presented in Figure 6. Prestressed concrete box-girder bridges with hollow rectangular piers monolithically connected to the deck, constructed using the cantilever method, is the most frequent typology (25%) due to the site topography (mountainous area). Simply supported bridges where the prestressed concrete beam deck is supported on hollow rectangular piers through elastomeric bearings are the second most frequent class in the inventory, while single span and box-girder bridges with cylindrical single-column or multi-column piers monolithically connected to the deck are also frequently encountered in this inventory (Figure 6). Fragility curves of the generic (representative) bridge of #232 and #221 classes (namely bridges with hollow rectangular piers connected through bearings to prestressed beam deck and monolithically connected to box-girder bridge deck, respectively) are depicted in Figures 7 & 8, along with upper and lower values (dashed lines -range of thresholds) for each limit state. As far as the #232 bridge class is concerned, the variation of upper and lower level fragilities from the fragility curve of the generic bri for LS1. In general, the use of the fragility curves of the generic bridge for all those in the same category may underestimate or overestimate fragility by up to 35%, however in some cases (i.e. LS1 for bridge class #221 and LS4 for #221) the underestimation may reach 50%.
Software for the estimation of bridge-specific fragility curves should be applicable to different bridge types and structural systems. Therefore, capacity (limit state thresholds) and demand estimation should be both structure-specific and parameterized in order to cover a wide range of different components, ensuring accuracy in results and wide application range. The use of generic bridge fragility curves for all bridges belonging to the same category may underestimate or overestimate fragility, typically by up to 35%, however in some cases the underestimation may reach 50%, which is clearly an issue of concern. The range of LS threshold values is fairly narrow for lower limit states, but it increases for higher earthquake intensity and higher limit states (heavy damage, failure).
Research Funding Program: ARISTEIA II: Reinforcement of the interdisciplinary and/or inter institutional research and innovation.
This research has been co-financed by the European Union (European Social Fund – ESF) and Greek national funds through the Operational Programme “Education and Lifelong Learning” of the National Strategic Reference.
Author declares that there is no conflict of interest.

©2017 Stefanidou. This is an open access article distributed under the terms of the, which permits unrestricted use, distribution, and build upon your work non-commercially.