Experts have observed Cadmium as one of the most toxic metals with carcinogenic and tetrogenic impacts. The main foundation of Cd contamination in agricultural soils is the extensive application of mineral phosphorous fertilizers, fungicides and sewage sludge.1–3 experts has observed that Cadmium is bound to permanently charged surfaces of clay minerals, to surfaces of hydroxyl groups along the edges of clay particles, it also includes to phyllosilicate clays,4 to Fe and Al (hydro)oxides, and to phenol and carboxyl groups of soil organic matter.5 There are several Factors that pressure cadmium mobility in agricultural soils are e.g. tillage practices, duration of the cadmium– soil interaction, soil type and layering, water flow and solute transport distribution between the– macrospore and matrix domain, rain/irrigation intensity, total and active CaCO3 content, organic matter content, as well as pH value of the soil solution.6–10 It has been assumed that the movement of heavy metals requires the metal to be in the soil solution. For that reason, physical mixture through ploughing of the soil surface during repeated cultivation is the main factor that contributes to an increase in the concentration of heavy metals beneath the zone of application. The preferential paths for water flow and solute transport in the unsaturated zone of soil are the hydrologically effective (= surface vented) macrospores: biopores (e.g. earthworm, ant, and root holes), inter–aggregate pores, and desiccation cracks.6,11–15 Soil is a natural body consisting of layers (soil horizons) of mineral constituents of variable thicknesses different from the parent materials in their morphological, physical, chemical, and mineralogical characteristics.16,17–22 Soil is also a multiphase mineral and organic porous media consisting of three phases: solid, liquid and gaseous. The solid phase consists of particles of various distribution generated by partitioning of rocks by different environmental (erosion, transport, deposition), thermal and chemical processes. There are three main types of soil particles distinguished: sand, silt and clay. The relative amounts of each fraction in the soil sample, sorted according to its size (particle diameter) are presented by particle size distribution or grain size distribution.23 Soil particles are usually packed loosely, with different, even unique three dimensional spatial orientation, thus creating a soil solid structure filled with empty pores, which may be occupied by fluids – liquids or /and gases. The fraction of void space in the porous material/soil is defined by porosity ratio.24–26
Developed model
(1)
Substituting solution into (1), we have
(2)
(3)
(4)
(5)
Considering when
(6)
(7)
(8)
(9)
This implies that equation (10) can be expressed as:
(10)
(11)
(12)
(13)
(14)
(15)
(16)
(17)
(18)
(19)
(20)
(21)
(22)
Applying quadratic expression, we have
(23)
Where, and
(24)
(25)
(26)
(27)
(28)
Substituting equation (20) to the following condition and initial values condition.
(29)
Therefore, (30)
(31)
(32)
(33)
But if
Therefore, equation (33) can be expressed as:
(34)
Results and discussion are presented in tables including graphical representation of cadmium concentration at different Depth and Time (Tables 1–4) (Figures 1–4).
Depth [M] |
Predictive cadmium
concentration [Mg/L] |
Experimental
cadmium concentration [Mg/L] |
3 |
2.87E– 06 |
2.80E– 06 |
6 |
4.74E– 06 |
5.50E– 06 |
9 |
6.62E– 06 |
6.20E– 06 |
12 |
8.49E– 06 |
8.01E– 06 |
15 |
1.03E– 05 |
1.13E– 05 |
18 |
1.22E– 05 |
1.23E– 05 |
21 |
1.41E– 05 |
1.50E– 05 |
24 |
1.59E– 05 |
1.47E– 05 |
27 |
1.78E– 05 |
1.64E– 05 |
30 |
1.97E– 05 |
1.91E– 05 |
33 |
2.16E– 05 |
2.06E– 05 |
36 |
2.35E– 05 |
2.25E– 05 |
Table 1 Predictive and experimental values for cadmium concentration at different depth
Depth [M] |
Predictive cadmium
concentration [Mg/L] |
Experimental
cadmium concentration [Mg/L] |
3 |
1.63E– 01 |
1.65E– 01 |
6 |
3.33E– 01 |
3.11E– 01 |
9 |
4.89E– 01 |
4.45E– 01 |
12 |
6.52E– 01 |
6.52E– 01 |
15 |
8.15E– 01 |
8.18E– 01 |
18 |
9.77E– 01 |
9.54E– 01 |
21 |
1.40E+00 |
1.52E+00 |
24 |
1.30E+00 |
1.37E+00 |
27 |
1.47E+00 |
1.52E+00 |
30 |
1.63E+00 |
1.69E+00 |
33 |
1.79E+00 |
1.82E+00 |
36 |
1.95E+00 |
2.03E+00 |
Table 2 Predictive and experimental values for cadmium concentration at different depth
Time Per Day |
Predictive cadmium
concentration [Mg/L] |
Experimental cadmium
concentration [Mg/L] |
10 |
7.14E– 05 |
8.58E– 05 |
20 |
1.43E– 05 |
1.41E– 05 |
30 |
2.14E– 05 |
2.27E– 05 |
40 |
2.86E– 05 |
2.73E– 05 |
50 |
3.41E– 05 |
3.49E– 05 |
60 |
4.10E– 05 |
4.15E– 05 |
70 |
4.77E– 05 |
4.66E– 05 |
80 |
5.45E– 05 |
5.66E– 05 |
90 |
6.13E– 05 |
6.72E– 05 |
100 |
6.82E– 05 |
6.68E– 05 |
110 |
7.49E– 05 |
6.94E– 05 |
120 |
8.17E– 05 |
8.03E– 05 |
130 |
8.86E– 05 |
8.88E– 05 |
140 |
9.54E– 05 |
9.42E– 05 |
150 |
1.02E– 04 |
1.09E– 04 |
160 |
1.09E– 04 |
1.19E– 04 |
170 |
1.15E– 04 |
1.31E– 04 |
180 |
1.23E– 04 |
1.33E– 04 |
190 |
1.29E– 04 |
1.39E– 04 |
200 |
1.36E– 04 |
1.41E– 04 |
Table 3 Predictive and experimental values for cadmium concentration at different time
Depth [M] |
Predictive cadmium
concentration [Mg/L] |
Experimental
cadmium concentration [Mg/L] |
3 |
3.85E– 04 |
3.66E– 04 |
6 |
7.71E–04 |
7.44E– 04 |
9 |
1.15E– 03 |
1.12E– 03 |
12 |
1.54E– 03 |
1,45E– 03 |
15 |
1.92E– 03 |
1.88E– 03 |
18 |
2.31E– 03 |
2.22E– 03 |
21 |
2.71E– 03 |
2.57E– 03 |
24 |
3.10E– 03 |
3.22E– 03 |
27 |
3.47E– 03 |
3.54E– 03 |
30 |
3.85E– 03 |
3.77E– 03 |
33 |
4.24E– 03 |
4.34E– 03 |
36 |
4.62E– 03 |
4.67E– 03 |
39 |
5.01E– 03 |
5.11E– 03 |
42 |
5.40E– 03 |
5.35E– 03 |
45 |
5.78E– 03 |
5.66E– 03 |
48 |
6.17E– 03 |
6.22E– 03 |
51 |
6.55E– 03 |
6.44E– 03 |
54 |
6.94E– 03 |
6.88E– 03 |
57 |
7.32E– 03 |
7.37E– 03 |
60 |
7.71E– 03 |
7.55E– 03 |
Table 4 Predictive and Experimental values for cadmium concentration at different depth
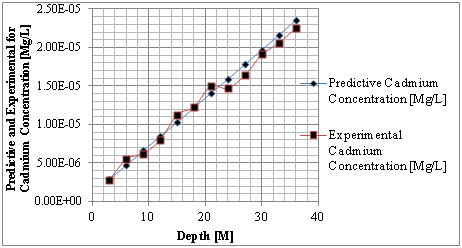
Figure 1 Predictive and experimental values for cadmium concentration at different depth.
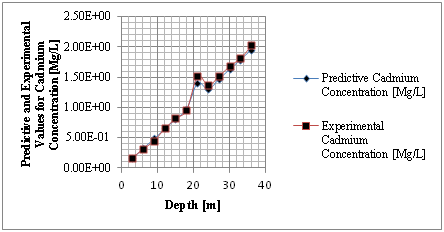
Figure 2 Predictive and experimental values for cadmium concentration at different depth.
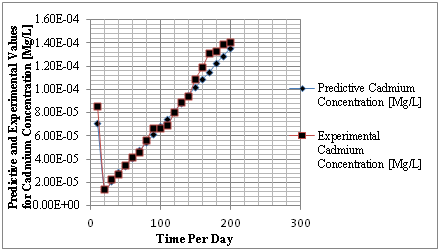
Figure 3 Predictive and experimental values for cadmium concentration at different time.
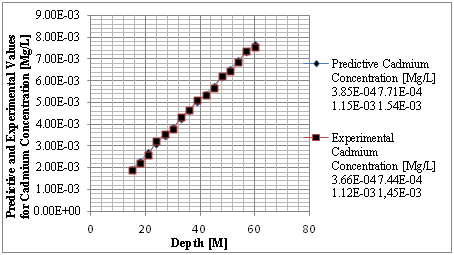
Figure 4 Predictive and experimental values for cadmium concentration at different depth.
The study from graphical representation shown in figure I express how the deposition of cadmium linearly increasing with change in depth at different depositions to the optimum rate recorded at 36m, the formation at this level experience progressive increase of concentration, these are reflected on predominant homogeneous structure of the strata, comparison between predictive and experimental values developed favorable fits, while figure two observed similar condition as exponential phase were experienced in the deposition of cadmium in different formation, the optimum values were also observed at 36 metres, comparing figure two to one, the concentration are much higher, it implies that the degree of porosity are higher than figure one. Both parameters developed favorable fits for model validation, while figure 3 developed linear increase to the optimum level recorded at 200 days, these condition implies that the system considered the migration at different time, the depositions of cadmium were observed to migrate to phreatic zone with higher concentration at two hundred days, the reality were observed from the degrees of porosities deposited at different depths, validation were observed to developed best fits between the predictive and experimental values. Figure four monitor the system at progressive transport to deeper depth, these were to determine their rate of increase or decrease in concentration, homogeneous rate of concentration were observed, but with slight heterogeneous experiences on experimental values that validated the predictive results.


