Masonry remains today an essential, even indispensable at buildings in Morocco, however, the lack of experimentation led to the neglect thereof in digital computing models especially the panels with openings. On the other hand, damage in seismic zones showed a significant participation of this panel on failure modes. It is noteworthy that the Moroccan seismic regulations RPS 2000 Reviewed in 2011 advocates modeling masonry infill panels with two equivalent rods [cf. Art No. 7.3.3].

Keywords: masonry opening, equivalent strut, infill frame

The infill elements whatsoever clay brick or concrete blocks, with or without openings are neglected in all research departments in conventional buildings. Indeed, engineers design numerical models via columns and beams systems mixed with bracing sails without an interest in infill masonry elements (as by their dead load) that of the nature, or the parameters of openings therein.

Although the infill is responsible for breaking by shear forces and/or torsion-flexure many frames and hence collapse under earthquakes. In addition, openings, such as windows and doors change already behavior of the panels, depending on several criteria (size, position...) The simplification done is extremely reductive, masonry that considers as non-structural element may in some cases lead to dangerous structures during earthquakes.

In an attempt to understand this issue, a study was conducted through the modeling of the infill elements with openings of a real project with ten floors, while treating the effect on the seismic behavior and the intrinsic characteristics of structures (fundamental period-rigidity, horizontal base shear forces, alteration of internal forces). The exhaustive literature review addressing the different analytical and experimental research on masonry interacting with the framework, the model of the strut was deemed suitable for modeling infill panels.^1-9

At this stage, the analyses were performed in the linear domain. First, it should present the demonstration procedure for the validation of the finite element model and the choice of the equivalent diagonal model based on an experimental study by researchers Afefy and Taher to move to the introduce effect to the opening in panels by a reduction coefficient.

Frame studied by Afefy and Taher (Reference frame)

The RC frame is shown in figure below; the infill panel is composed of thick red bricks 120mm. the concrete used is B25 (25MPa), and the mortar compressive stress is 10 MPa. A horizontal force at the top of the left column loads the frame. Based on the method described in paragraph 3.4 of Eurocode 6 P1-1, results of calculation of the masonry are:

1. Resistance characteristic of the brick: Rc= 6 MPa.
2. Resistance declared characteristic of brick: fb= Rc=7, 08 MPa
3. Compression strength of masonry: fk = K*.fb^0,7.fm^0,3 = 1,57 MPa
4. Modulus of masonry: Em = fk. Ke with Ke=1000 is Em=1570,56 MPa

Note: the characteristics of masonry and mortars are from laboratory testing in Moroccan projects during the 2014-2015.

Models diagonal used

Smith and Carter 1969

Holmes 1961: = (4) 2.2.6 Mainstone with eccentricity

Modeling of finite element calculation software (SAP2000)

In the actual behavior of the completed framework, for some value of the load separation between the frame and panel takes place in the tension zone (see figure) (Figure 1-11). Therefore, to address this important parameter impact on the results, it is necessary to model the interface as follows:

Figure 1 Geometry and the reinforcement beam (Afify, 2008).

Figure 2 Frame-panel Separation.

Figure 3 RC frame-panel Separation.

Note: For greater heights this approach is reviewed.

Figure 4 Diagram load-displacement for different models.

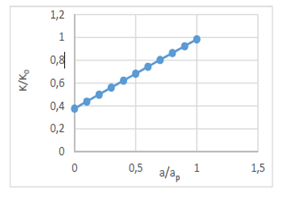
Figure 5 Standard Lateral stiffness as a function of rod width ratio.

K: lateral stiffness of the infill frame with opening

K0: lateral stiffness of the infill frame without opening

a: the strut width reduced relative to the Paulay & Priestley model

ap: width of the Paulay & Priestley strut.

Figure 6 Different positions of the opening.

Figure 7 Capacity Curve (pushover).

Figure 8 Capacity curves of the bare frame and in filled with different models

Figure 9 Comparison of elastic shear forces.

Figure 10 Comparison of initial stiffness K0 different models.

Figure 11 Comparison of ultimate resistance Vu.

In the compression zones, define a connecting element ("Gap" for SAP2000) to take account of the presence of the mortar between the RC frame and the masonry panel, by introducing the following parameters:

Between nodes link direction according to the local coordinate system of the element ie U1.

The effective stiffness calculated using the formula (Table 1-5):

A_mor*E_mor

Where: A_mor mortar contact surface

E_mor: Young's modulus of the mortar

t_mor: thickness of the mortar

In traction areas, two scenarios are possible: first place, generalizing type links "Gap" across the contact interface. In addition, in a second place, unlink nodes in the tension zone.

Finite element model validation

The exercise done in numerical modeling shows that the FE model created with and without separation (RC frame and panel) loading gives relatively close results of those from experience by Afefy &Taher.

Choice of diagonal model’s

The results obtained for the different models are shown in a diagram with the finite element model (reference model). According to the diagrams, the model diagonal closest to the finite element model is the one proposed by Paulay and Priestley. The average error between the latter two is of the order of 3%.
The Paulay and Priestley model is then adopted for the future.

Effect of openings

Note: the opening explored in this chapter is a rectangular window type.

The effect of the openings is discussed in some detail the way through finite element model with separation validated previously. And by studying several parameters related to openings and influencing the linear elastic behavior of the infill masonry frame.

The parameters in this analysis are:

1. The percentage occupation of the opening area,
2. The geometric shape of the opening (orientation)
3. The position of the opening in the panel.

The literature search asserted that the openings have a reducing effect on the lateral stiffness of the infill masonry frame. Therefore, researchers have considered appropriate to introduce the equivalent effect on the equivalent diagonal through reduction coefficients applied to the width thereof.

Effect of the opening form: To study this parameter, the following openings were chosen: S= 0,5x1 m²; 0,5 x 1,5 m²; 0,5x2 m² ; 1x1,5 m² ; 1x2 m² ; 1,5x2 m². Then reversing these dimensions.

The relationship between the normalized lateral stiffness and the ratio of diagonal widths follows a linear curve, using the following equation:
y = 0,6061x + 0,3806

While the relationship between the normalized lateral stiffness and the size of the opening can be approximated by a polynomial of order 2 curve:
y = 1,6556x2 - 1,8506x + 0, 9771 (7) with a correlation coefficient: R² = 0,9952.
α is the percentage of area occupied by the opening compared to infill panel area.

The end result:

Based on these results, the error average outcome of this comparison is 3.6%. To this end, the form of the opening can be neglected.

Effect of the size of the opening

All constructions in Morocco use masonry as separating elements, following the recommendations of the DTU 20.1 20.13 and 21 relating to masonry, openings are still confined via stiffeners reinforced concrete around. This configuration gives the infill panel rigidity and replaces the derived portion thereof. However, tests carried out in the literature do not allow to properly assess the behavior of the panel with opening stiffened, particularly in Morocco.

The exercise will be done for panels with openings without stiffening reinforced concrete. The size of the opening has a big influence on the behavior of RC frame with masonry. And given that the geometric shape of the opening does not have a great effect on the overall behavior of the infill part was considered studying square central openings in different sizes (ranging from 10% to 60% of the surface of panel).

K: lateral stiffness of the infill frame with opening K0: lateral stiffness of the infill frame without opening

a: the strut width reduced relative to the Paulay & Priestley model

ap: width of the Paulay & Priestley strut.

The coefficient size is defined by.

Effect of the position of the opening.

The proposed locations are: top right, top center, top right, middle left, middle center, middle right, bottom left, bottom center and bottom right.

To study the effect of the position, it is based on a central opening of 5% of the panel area. Therefore, the obtained coefficients have been calibrated in such a way to have a coefficient of 1 for the case of the central middle position.

Effect of Infill Panels with Opening on the Rc frame behavior In real study

The building studied is reinforced concrete (area of 425 m2). It is located in an average seismicity zone (zone II in speed and acceleration) with10 floors mainly dedicated to offices building.

Masonry used is characterized by a compressive strength:

The effect of the openings is introduced by reducing the width of the equivalent diagonal according to the results of linear elastic study. The infill was neglected for the frame whose percentage occupancy of the opening is greater than 60%.

Effect on the natural period

In addressing the effect of masonry on the natural period of the structure considered in this case, modeling infill gave an average reduction of the natural period of up to 64% compared to structure without infill. In addition, the introduction of openings reduced the effect of the masonry.

Effect on the displacement

In terms of the global displacement of the building, the presence of the masonry induced a remarkable decrease. On average, the maximum displacement in the X direction is reduced by 82% for infill without openings, and 70% for the case with central opening. The presence of the openings increases the displacement of 45% compared to the infill panel for the model adopted in this study. The masonry infill panels without opening give an average reduction of inter-story displacement of up to 71%, against 63% for infill with openings.

Masonry stabilizes the building against overthrow

Indeed, it gives an average reduction of θ index (reversal index in the RPS 2000 V2011) 68% for solid panels and 64% for panels with openings. As previously reported, diagrams drawn above were drawn in the linear elastic domain for several reasons, first is the not mastery of the dynamic masonry behavior without experimentation. Thus this study was limited in that domain. But during a violent earthquake materials do not remain in their elastic state, therefore, the linear approach can provide only limited understanding of this behavior and the consideration nonlinearities is essential for a proper assessment of the behavior seismic structures. This leads to do a non-linear structure analysis with the Pushover method (progressive push).

Analysis of pushover

The pushover analysis is basically an approximate nonlinear static analysis, performed under increasing horizontal loads, a monotonically distributed throughout the height of the structure according to a predefined model, until the ruins models begin to appear. During this analysis, gravity loads remain constant. The result of the push over analysis is a curve, which gives the load at the base of the structure according to the movement in the latter top, this curve is called capacity curve or curve push over.

Consideration was given to a representative study of a structure braced frame by frame limited to 6 levels based on the architectural plans of a real study, calculation of reinforcement in the frame was done according RPS2011 BAEL99 regulations. The distribution of the lateral force is a subject which differs from its principles in codes (FEMA 273, EC08, and RPS2011.) for nonlinear static analysis which is based on the relationship demand-capacity, distribution of force depends on the mass inertia and the transition to a system with one degree unknown. In RPS2011, the lateral force is described as follows:

According RPS2011, lateral seismic force is expressed as follows:

Where:

Speed zones coefficient.

Site Coefficient

D: dynamic amplification factor.

I: Priority Coefficient

K: behavior factor

W: The load taking into account the weight structure.

Distribution of efforts on the floors

The seismic lateral force will be spread over the floors of the building. We write (RPS2011):

T: the fundamental period of the structure

It is particularly interested in the effect of the presence of the masonry infill on the seismic behavior of the RC frame. During Pushover analysis, we begin by modeling the masonry infill model Paulay and Priestley and then passes Mainstone model, and finally the model shifted Mainstone. Based on the capacity curves are compared mainly, results for the elastic limit state (Vy, dy, K0) and those relating to the strength limit state (Vu, du).

1. Elastic limit State

We note an increase in the elastic shear (Vy) to the frame with infill from the bare frame. The increase is 311% for the Paulay’s model and 358% for Mainstone’s model and 267% for shifted Maistone’s model.

Regarding the initial stiffness K0, the largest increase is that of Paulay model which equal to 870% of the initial stiffness of the bare frame, and the model of Mainstone, it is 463% and the growth of the initial stiffness of the frame if the shifted Mainstone model is equal to 236%. b-the strength limit state. For the ultimate limit state of resistance, we note the increase of the ultimate shear force Vu and decreased displacement of the ultimate limit for all models compared to the bare frame. For the model of Paulay, increasing Seen is 259% and the decrease in the limit displacement is 90%, on the model of Mainstone increasing Vu is 463% and decreasing the limit displacement is 87%, and for the shifted Mainstone model with increasing Vu is 176% and the decrease in the displacement of the was 79%.¹⁰

Certainly, masonry provides a gain in terms of strength and rigidity to the structure. However, it causes a considerable lack in terms of ductility of the structure when it is subjected to a strong earthquake. Also by acting on the internal forces in nodes, something that changes the way of destruction of the brittle ductile structure. In the example studied, the openings were chosen (by lack of locally experimenting) a central rectangular window types, while other types of opening will be the subject of future research.

From this retrospective, infill masonry walls is pointed out that only a low resistance in comparison to that of the structural elements and allowing a contribution in rigidity and strength in the plastic domain, but giving place to the structural elements in post-elastic domain to dissipate seismic energy by ductility. This compromise between gain in strength, stiffness and loss of ductility induced by infill masonry remains a potential research subject.

None.

The author declares no conflict of interest.

1. Goutam M, Sudhir K. Lateral Stiffness of Masonry In filled Reinforced Concrete (Rc) Frames With Central opening. 2008.
2. Benamar A, Akarbich A, Ben Akka M. Modelisation deselementsderemplissage En Maconnerie Dans Lesbatiments A Grande Hauteur. Morocco: Ecolehassania Des Travaux Public; 2015.
3. Sachin S, Hermant B. Masonry Infill Rc frames With Openings: Review Of In–Plane Lateral Load Behaviour and modeling Approaches. The Open Construction and Building Technology Journal. 2012;6:126–154.
4. Lefebvre K. Behavior Study Under Lateral Loads Of Concrete Frames With Masonry Infill Walls, Built Before 1960, Thesis Presented At The École De Technologie Supérieure As Partial Requirement For Obtaining The Doctorate In Engineering Ph.D. UK: School Of superior Technology University Of Quebec; 2008.
5. Nf En 1996 Eurocode 6: Calcul Des Ouvrages En Maçonnerie. Le Règlement De Construction Parasismique Rps 200–Version 2011.
6. Favvatamj, Karayanis. Influence Of Infill panels with and without Openings on the Pounding Effect of RC Structures. Greece; 2012.
7. Ourabah A, Hamouche S, Seghir A, et al. Pushover Analysis of a Freestanding Structure. 2010 International Symposium on Building Seismic Zone. Algeria: Benbouali Hassiba University of Chief; 2011.
8. Thomas Telford. Rc Frames Under Earthquake Loading: State Of The Art Report, Comité Eurointernational Du Béton. 1996.
9. Benamar, Htiti Y, Thitih N. Implementation of the Rps 2011 to Common Buildings. Morocco: Study of Masonry with Openings And Seismic Behavior Mohamadia School; 2015.
10. Elouali T. Effect of Infill Masonry Panels on The Seismic Response Of Frame Buildings. Proc ASCE Structural Division Journal St–1. 1998;92:331–403.