In descriptive and projective geometry, the concepts of modelling or remodelling cannot be simplistically defined and applied through graphic operations based only on formal results or visualisation. The discussion of a scientific result as concerns descriptive drawing has the scope of obtaining an image or more than one image projected on planes and in space, as they derive from specific and regulated geometric operations and from in–depth reports related to the investigation of the object of study. The graphic–geometric aspect concerns a question that first and foremost is regulated by a method defined by the main bi–univocal relation between projection and section and, consequently, by an application of the procedure related to the system of representation. To draw or represent scientifically signifies penetrating into the knowledge of an entity or an object, while respecting its intrinsic rules. There can be no scientific basis if the procedure is not preceded and supported by an acquired and codified methodology. Modelling signifies going back to knowledge, a fundamental condition for representing the entire graphic–geometric process that also implies the knowledge itself of the investigated object. To the concept of remodelling is also juxtaposed that of virtuality and in this way it is possible to discuss in scientific terms in order to determine the relationships referring to the investigation carried out on an object in the dual relationship of model: the first understood as technical – scientific structure acquired also from its history of codification, the second the result of a process of experience in which the model itself becomes concrete and explicit in its image projected on planes or in space. The scientific nature of a program of research and of consequent operations of study cannot be such if the graphic and geometric terms are not compatible with all of the steps of a methodology and subsequently of a procedure. This is a question of necessity to understand and know through the image, the form and, consequently, the object acquired through an introspective process determined also by the unification of the methods of representation, as well as by the type of investigation that has allowed us to understand, know, and draw how the object is constituted in its various parts and in its entirety.

Keywords: graphic – geometric models, homological relationships, virtual remodelling in descriptive geometry, drawing to understand and know

The object of this discussion is to highlight the need to consider the object, even if architectural, in purely theoretical terms of the research, basing one’s approach on the concept of remodelling and virtuality, considered within the discipline of descriptive and projective geometry. In every science, as in every area of knowledge that addresses the concept of remodelling, this takes on a significance that is first investigated and then applied to various study cases. This definition contributes to soliciting and comparing strictly theoretical, but also concrete, questions. For example, the concept of modelling and of formulating remodelling in the mathematical and analytical systems for hydraulic studies is applied to the calculation of the similitude to compare the processes between reality and model. Even the concept of virtuality takes on indications analogous to those of remodelling: in fact, this is a set of experiences that are juxtaposed in parallel since for both there is set an indissoluble principle of graphic–geometric expression. For example, virtuality is construed as an analytical operation in the mathematical methodology and procedure relative to calculation in the science of construction. It is an acquired and codified rule that is useful in the resolution of structural systems composed both of rigid and deformable elements, and is applicable to materials with linear, flexible and non–linear behaviour. In descriptive geometry the determination of the aspects concerning remodelling and virtuality first considers the structure of the model defined by the system of representation and then by the determination of the image that, reproduced, in turn forms another model, and consequently obtains the visualization of the object on the plane and in space. In this way the concept of model, understood as in its duplicity, is the key that allows one to open to investigate, juxtapose and consider remodelling in the principle of virtuality. The models become explicit in the relationship that they establish as a set decreed by their possible graphic–geometric solutions. In some cases, the processes of modelling allow for the preservation of their formal characteristics relative to the represented object. In fact, in the absence of substantial changes, to the morphological or functional characteristics of the represented object, the projection of the images can ensure the preservation of their true size and/or of their true shape (the shapes as related to the metric measurements of the object). In other graphic–geometric operations, a remodelling follows the loss of the metric values, just as there can be descriptive geometrical aspects in which in the same model understood as the structure that contains the values (metric) of true size, for other projections even other, non–metric values hold. Finally, we should not interpret virtuality as an analogy referring to simulation, as this last term is the result of presumed systems due to mere reproduction of images, as typical of those exclusively procedural, formal, exterior and fictional aspects that are not methodological and therefore not scientific.^1–5

The materials related to this research concern both direct and indirect aspects. The direct questions concern the acquisition of experiences and reflections articulated and developed over the years. The indirect aspects concern bibliographical sources referred to in this paper.^6–8 The study method develops on various registers, descriptive and comparative, held together by drawing. In fact, the fundamental role of drawing is to be articulated through descriptive geometrical thought and to initiate a process of introspection, of decomposition, and of comparison of the object, even when this is the architectural object. The data thus obtained during the study phase supply concrete values for a deeper understanding of the object. The research method has always developed in a parallel way to include thought, drawing and investigation, verifying step by step the knowledge and comparison amongst various facts, finding forms of compatibility between drawing and investigation and representation of the latter. The concepts of remodelling and virtuality have meaning and significance in research if they are considered in relationship with the objects, with the need to represent them as, for example, an architectural object not understood as a theme, or topic, but rather as a particular fact of such introspective interest as to be able to carry out a study through its properties and its characteristics deemed useful for drawing out and defining its reality, and not to perceive only the object, because mere perception would be insufficient. To carry out this particular type of investigation, one must undertake a further and essential consideration. This is a matter of studying the object in its complex reality and comparing it, even virtually, as demonstrated in drawings. Here we describe the basis or, rather, the strictly theoretical reasoning that, before all else, must shed light on the systems of representation considered fundamental for demonstrating the complexity of a study compatible with the complexity of the investigated object. The study in question has been started a few years ago and refers to the research of the introspective graphic representation of the object, be it architectural or belonging to engineering mechanics. The principle is based on the philosophical studies of Edmund Husserl on the discussion "The whole and the part" and on the observations of Professor Mauro Lena concerning "The architectural object". For now, there is no specific literature on the matter; there are some studies of particular interest that also concern the ways of representing with graphic, conceptual and abstract codes elaborated by Christopher Alexander, starting from: "A Pattern Language" and "Notes on the Synthesis of Form".

The following discussion is meant to offer some observations arrived at through a scientific path concerning the systematization and inseparability of the graphic and geometric methods and procedures of representation believed necessary for describing the process of understanding relative to the effects of modelling and remodelling. At the same time, we observe the causes that contribute to introspectively representing the real and/or virtual object located on the plane and in space. The object, in general, is understood as a real fact and therefore is analysed like a set that defines multiple and ample relationships that mainly concern the construction of physical as well as perceived space. In this way, shapes, images, and figures are determined, which interpret the object through a set of events that organize and contribute to defining other, and again multiple, relationships. The object, in synthesis, emerges from the duplicity of relationships given by the space in which it is inserted and with which it is compared, according to areas deduced from its nature. In addition, this is felt through known reality, perceived and interiorized; one passes therefore from hermeneutics, that is from a sort of interpretation concerning the object, be it architectural or generic, which in its multiple causes due to operations of decomposition and consequently of re–composition and comparison amongst its single parts with its successive and still further parts that have in turn been split. This process of fractionation allows one to learn about new parts of the object, to examine them individually and understand how to find ways to juxtapose them with other parts, in turn dismantled, and compare these various data. These operations also lead the researcher to acquire subjective values. This last aspect must be the result of a cultural approach that relates to the formation of him or her who observes the investigated object in its different and positioned phases and/or parts. These various levels of operations, carried out according to graphic–geometric principles and rules, continuously remodel the investigated object in continual variations both in terms of position, of metric and non–metric values, and of perception. Thus, the remodelling of the object and of its single parts is reconfigured through graphic processes that also determine aspects of the object itself which take on a connotation of effects due to the principle of virtuality. The concept of virtuality dates to the second half of the eighteenth century, and is a mathematical principle of a comparative nature used in the methodology of the science of construction. The concept of virtuality should not be confused with that of simulation. It would be an error to consider the virtual process associable with formalistic results and without foundation and easily changed. For example, let us consider the drawing referring to a model in parallel projection, recognized for practical and applied reasons like axonometry. This returns to us through historical thought, also due to Cubism, the immediacy of representing through oblique axonometric drawing the various positions relative to the elements that constitute the generic object or architecture under investigation. In fact, cultural research, in particular that related to Cubism, fully complies with the theoretical sphere of representation and perception, and in this way of observing and studying the object as an aesthetic phenomenon using, graphically, parallel projection, or rather its direct application in axonometry, gives us a modelling that permits us to understand the reality that we know, transferred to representation in space. Axonometry, thus considered, is to be understood as a remodelling since its effects allow us to define the object and its individual parts not only through a simplistic transcription, but rather taken apart, investigated, penetrated and, finally, reconstructed. “The purpose of knowledge is to translate reality into an understandable form and to express it in a suitable system of signs, thus a world is built.” This world is formed with structures and orders, with non–real (virtual) signs that take on the meaning and intent that we attribute to them, because only the object is real. In this experience, too, we can look back in history and consider the intellectual journey of Le Corbusier, and before him of Eugène Emmanuel Viollet–le–Duc, as well as that of Auguste Choisy, with regard to the use of oblique drawing considered useful for representing the architectural object. After this introduction, which is a synthesis regarding the cultural use related to axonometry, our discussion will focus on the validity of remodelling of virtuality, which puts the descriptive geometric structure of parallel projection at the centre of the question presented here (Figure 1).

Figure 1 Drawing a model in parallel projection (drawing, by Andrea Donelli).

The object initially dealt with and studied in its geometric reality, represented in true scale and true form, finds its scientific and concrete confirmation as a geometric model, as it is the result of a projection operation and a consequent image on the plane. This is the noted example of Monge’s method and procedure of double projection. The geometric model was, in that way, described and delineated according to logical canons belonging to the methods and procedures of graphic descriptive geometry. Monge’s double orthogonal projection fixes a dual relationship between the entities and the sizes which metrically preserve the model, that is a system of one principle and one geometric structure, which in turn retains the model of the image since it is derived from the relationship of projection and section of the operation of transmission of the entities on the planes. In this case we will also have a relationship due to a simple homology, whose significance is due to the logical correspondence between two things, and therefore what occurs in one is repeated in the other, because of the same logic. Of particular interest in the processes of remodelling and virtuality of the models is the exercise referring to orthogonal projection with homology and the consequent reversal of the tract t_α'' on the plane π'. In this case, one obtains the tracing of the volumes of the entire system, even the volume of the figure overturned on plane π'. The volumetric model obtained in this way corresponds to a remodelling and virtuality integrated with the system (Figure 2).

Figure 2 From one system to another: drawing of the following models: from a parallel projection to the orthogonal projection with the homology and the subsequent overturning of the plane α. (drawing, by Andrea Donelli).

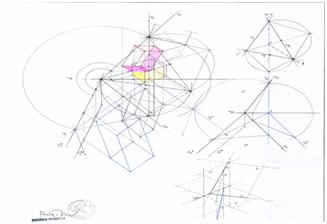
In this bi–univocal relation decreed by orthogonal projection with homology, one can consider a possible question of remodelling due to possible and non–random variants related to the new image of the model defined by the image in the way and in the position in which it is determined. The processes of representation in orthogonal projection with homology make it possible to determine the relationship of remodelling and of virtuality in the models referring to the reality of the object. In considering the unification of methods of representation it is possible to determine the effects of virtual remodelling in descriptive geometry starting from parallel projection, relating to orthogonal projection with homology with the resulting overturning of the planes. These operations constitute the continuity and the inseparability of the methods and procedures. In this way, one obtains additional images due to the modelling and remodelling of the systems, as these are defined by graphic–geometric steps or processes. The reciprocity and duality relative to the graphic–geometric properties allow one to preserve and consider, in geometric methods, the reciprocal relationships aimed at the study and the introspection of an object (Figure 3); in this case one can also consider as an object, and further study, the architectural object. Considering the geometric structure of the model in parallel projection, through its indispensable rules for graphic–geometric operations, one constitutes the foundation on which to base the practical application of axonometry. In fact, we refer to orthogonal axonometry, as this is determined by the derivation and demonstration of the triangle of traces. This system, relative to the orthogonal model inherent in parallel projection, is determined by the structure of the system of the axial triads x'; y'; z'; and by its traces, or rather by the intersection of the planes that configure with the degrees of inclination of the angles in a bi–univocal relationship with the axes so that the model itself determines its own orthogonal axonometric characteristics.^9–12

Figure 3 Modeling in orthogonal projection and image conservation in true size. (drawing, by Andrea Donelli).

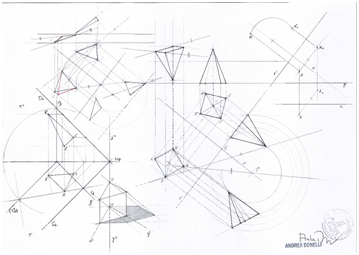
Given a system in orthogonal projection with homology, a relative graphic geometric model is shown to obtain an image of a figure in first projection positioned on the horizontal plane π 'in true size and in true form. Through the procedure related to the foundation of the projection and section, the entities and sizes are projected that construct the visualization of the model as an image on the remaining planes. The result that is projected and therefore displayed will be a three–dimensional figure (Figure 4). This last model will not have directly verifiable metric characteristics, but will be the result of equally proportioned and graduated non–metric values because they are derived from true sizes and a true form. In sum, this process highlights a connotative relationship of remodelling, and this determines a virtual confirmation as it is possible to define and place the object so represented on planes and therefore consider it as a virtual outcome because it is congruent with the reality to which it belongs. This collocation is also a sort of control and determination of the facts that are abstracted through the graphic–geometric method and procedure and made explicit for a particular study and cognitive investigation of the object.^12–15

Figure 4 Drawing of a model of a hexagon shaped conic shape in orthogonal projection with homology and double projection of Monge (drawing, by Andrea Donelli).

With the definition of object or architectural object, we intend to investigate, graphically and geometrically, those requisites that belong to the knowledge of space and to the recognisability of architecture. With the schematization of a figure that refers to a regular polygon, the object in question will be given by the relationship fixed by the reality we know through our experience and then transferred to the plane and to space through the representation that contributes to defining knowledge and judgement. This aspect becomes even more extensive and complex in the study when it comes to analysing an architectural object. To do so, one must acquire specific knowledge concerning the settlement type and the architectural, as well as the constructive and structural, type. From this last conclusive consideration, it can be summarized that the architectural or mechanical object or the architectural theme are represented according to the aspects and the principles that regulate and concern the codified graphic–geometric modelling. Where by model we mean it in its two fold and dual condition. The first condition is understood as a structure of the geometric system of reference, namely: axonometry, orthogonal projection, homologous projection, perspective. The second condition derives from the first and consists of the image of the object projected onto the planes. These two conditions related to the concept of modelling determine integration and therefore form a single model that can in turn replicate from one system to another or representing the object by images for different positions on the planes. It should be specified what to represent and what is meant to refer to a specific type of analysis that investigates in an introspective way the object or theme in question. For example if it is an element or a part, referring to a unit, in this case it will be necessary to think both in objective terms (as referring to the whole) and in subjective terms as the single unit assumes its own values and characteristics and autonomous. This discussion therefore forms a full part of the form related to the thought of research that observes the object and subjective aspects as they are areas that specifically concern a type of study. This study I am conducting is focused on the introspection of the object. This research still has many limitations, as it is a theme that I started a few years ago, and it is a little discussed topic so literature is scarce. The main and authoritative references can be found in the philosophical thought of Husserl (The whole and the part) and in the research of Professor Mauro Lena (The architectural object, and the composition). In conclusion, drawing, in this degree of experience reported here through its geometric models, expresses itself as communication through visible images that make mental images explicit, an essential condition in seeing and thinking about space, its representation for cognitive control, conceptual and abstract of the elements that make up the architectural and engineering project. The study related to the representation systems necessary to investigate the object or the theme of architecture or engineering intends to make use of the concept of virtuality because its representation and its description is based on the way of observing reality and articulating graphic models on principles that compete to measure themselves with reality itself. This aspect closely concerns the same attitude of the study that belongs to the science of construction, known through the principle of virtual works. From the exercise of science of construction the bending moment is reversed and considered as load. This virtual principle is such and therefore subsists because all this together always corresponds to reality because it is analytically compared to it. Otherwise it would be simulation as it is a condition that does not meet the requirements of reality but is a mimesis of the latter. The introspective design executed according to the rules of descriptive geometry is presented as a virtual concept because it is directly comparable with reality; it constitutes the connotations of the facts that are always found and not imitative as they occur in video modelling.^15–18

Parallel projection (axonometry), as with orthogonal projection with homology, since these are systems consisting of specific descriptive and projective processes, may be used for their graphical–geometric properties and articulations in studies concerning the architectural object. In fact, having available scientific methods of representation, it is possible to move from one geometric system to another. In this way it constitutes a whole, a unity, a sort of connotations related to the graphic–geometric methods necessary to carry out a particular type of study and investigation of the object. This phenomenological aspect, which also exists in the gnoseological realm in reference to the graphic–geometric experience, arises within the intuitive experience, which observes all those phenomena associated with the way of performing and describing an experience. In representing an object related to architecture or engineering the use of codified systems referring to geometric models such as axonometry, the orthogonal projection allows fixing the projected image in the way considered suitable for its clarity and communicability. This fact takes place when a certain theme is described in the field of representation through a graphic elaboration of project. On the other hand, as regards a form of introspective research concerning the study of an object, both architectural and mechanical, the representation related to codified systems can take on a particular value. The reality of the object as it is, has a dual aspect: the quantitative relative to its measurability, and the qualitative one inherent to its characteristics. Both these two forms belong to the very reality of the object. In the field of knowledge we can therefore investigate the object both in its objectivity that subjectivity. The objective scope allows to represent according to well–defined models both for clarity and for communicability. While in the subjective context the object will be disconnected and released from rigid forms and can be represented according to the characteristics that belong to its values. Starting from these assumptions, further investigations are still possible concerning the construction before representation codes in the topological field and then the application of the models related to representation systems useful to perform other forms of abstraction related to the representation of the object. Indeed, through continuous checks carried out to extract from the characteristics of the object the essential properties from the experiences that it holds, from this basis a further very complex phase for the architecture is born, as it is possible to undertake studies and research conducted on the architectural object that concern and refer to topology, to questions that involve new questions, on how to represent the facts in the graphic–geometric process between the relationship of reality and the effects of virtual remodelling. Finally, the investigation of the architectural object using the tool of descriptive and projective geometry, the constant relationship amongst the models made such by their graphic and geometric process is, in this way to be placed and defined as a continuous experience between the reality and virtuality of geometric and graphic models. Virtuality is directly compared to reality, and therefore it does not signify doing a simulation, since the latter is the result of a technicality, and does not correspond to reality not to the actual objectivity of the experience.

None.

I declare that the mansucricpt of “Effects of virtual remodelling in descriptive geometry” is not subject to conflict of interest as the figures , the texts are exclusively the work of the declaring author.

1. Aterini B. Representation of the sphere between scientificity and randomness, Editrice Alinea, Firenze, Italy; 2005.
2. Baglioni L. The method of mathematical representation in the analysis of planar quadrilateral meshes, in Descriptive geometry and digital representation: memory and innovation. In: Rossi M, editor, Mc Graw-Hill, Milan, 2012.
3. Brownson C. Euclid's Optic and its Compatibility with Linear Perspective. Archive for History of Exact Sciences. 1981;24(3):165-194.
4. Cardone V, Barba S. Graphic models of architecture and territory, Edizione Apogeo education, Maggioli Editore.Santarcangelo di Romagna (RN), Italy; 2015.
5. Catalano GM. A theorem for the unification of methods of the science of representation. In Disegnare. 1994;(8):29 -33, (1994).
6. Cundari C. drawing, edizioni Kappa, Rom, Italy; 2014.
7. Cundari C, Migliari R. Descriptive geometry from tradition to innovation, Edizioni Aracne, Roma, Italy; 2014.
8. Donelli A. Fundamentals of Descriptive geometry: applications for architecture and engineering. Journal of Structural and Civil Engineering Research. 2014;3(4):1-12.
9. Donelli A. A Graphical Comparison of the Historical Model Geometric Descriptive: the visible part of our future. Journal of Civil Engineering and Architecture Research. 2017;1873-1879.
10. Donelli A. Observations on the descriptive geometric drawing, Edizioni Aracne, Roma, Italy; 2017.
11. Donelli A. Drawing survey and representation Thinking analysis and synthesis of research experiences. Edizioni Aracne, Roma, Italy; 2017.
12. Enriquez F, Lezioni di Geometria Proiettiva, Edizioni Zanichelli, Firenze, 1926.
13. Fasolo O, Fasolo S, Fasolo M, et al. Homology and its applications to the design and technical representation of architecture. Edizioni Kappa, Roma, Italy; 1989.
14. Lena M. The architectural object, IUAV, Venezia, Italy; 1988.
15. Migliari R. Descriptive Geometry, Methods and constructions. Città Studi Edizioni De Agostini, Novara, 2009;(1).
16. Scolari M. Theories and methods of drawing. Città Studi, Milano, Italy; 1994.
17. Sgrosso A. The geometric representation of architecture: applications of descriptive geometry, UTET, Torino, Italy; 1996.
18. Ugo V. The construction of the architectural form, Clup, Milano, Italy; 2003.