In the present study, temporal and spatial drought-risk events are characterized using a Modified Surface Water Supply Index (SWSI) for upper Tana River basin, located in tropics, Kenya. Forty years (1970-2010) hydro-meteorological data for low, lower middle, middle and high elevations at eight hydro-metric stations was used to characterize spatial and temporal distribution of drought. The spatial drought distribution is obtained via interpolation of hydro-metric stations data using Kriging interpolation technique embedded ArcGIS 10.1 was used. The drought trends were analyzed using a non-parametric Mann-Kendall trend test. The results show that south-eastern parts of the basin are the most drought-prone areas at different drought severities and frequencies. Drought severity classes ranged from 1.69-2.22 to 3.39-4.17 and 2.68-3.21 to 4.37-4.96 in 1970 and 2010 respectively across the river basin. The south-western parts of the basin exhibited highest drought frequency ranging from 10.61 to 13.16 while the north-western areas gave frequency values ranging from 3.74 to 6.29. The findings of the study are applicable in Early Drought Warning Systems, prioritized water resources planning and management.

Keywords: upper tana river basin, swsi, drought severity, drought-risk events, mann-kendall trend test, drought frequency

Drought is a condition on land characterized by scarcity of water that falls below normal average or defined threshold level. Drought events are stochastic in nature. A drought event is considered to be a ‘creeping hazards’ because it develops slowly, it is not easily detected, covers extensive areas and it lasts for a long period of time with adverse impact on water resources, ecological systems, and socio-economic development.^1,2 The term drought has been defined differently in numerous applications.³ Drought characterization in terms of spatial and temporal domain and trend analysis with different time scales for drought prone areas within river basins has been explored.^4,5 However, such studies have not been done in numerous river basins in the world. The problem of drought has become more common especially in arid and semi-arid lands (ASALS).⁶ Drought is a hydrological phenomenon, stochastic in nature which is difficult to detect and usually affect wide areas for extended period of time.⁷ To understand drought events, they may be expressed in terms of indices using precipitation deficit, soil-water deficit, low stream flow, low reservoir levels and low groundwater level. Different sectors use the terminology in different scenarios. For example, a hydrological-drought occurs whenever river or groundwater levels are relatively low. In addition, water-resources drought occurs when basins experience low stream flow, reduced water reservoir volume and groundwater levels.

The water resources drought is influenced by climatic and hydrological parameters, characteristics of the water resource system and drought management practices. The hydrological drought, mainly deals with low stream flows. This drought adversely affects various aspects of human interest such as food security, water supply and hydropower generation.^8,9 A sequence of droughts may lead to desertification of vulnerable areas such as arid, semi-arid and sub-humid areas. Within these fragile ecosystems, water resources, soil structure and soil fertility are critically degraded due to the drought vents.¹⁰ The characteristics of any drought in terms of magnitude, duration and severity have not been clearly understood for numerous river basins in the world. Based on purpose of application, different drought parameters may be derived. For instance, the main parameters of drought phenomenon especially the most critical for design of water storage reservoirs are the longest duration and largest severity for a given return period.^11,12

Four distinct types of droughts are Recognized.¹³ These include the Hydrological, Meteorological, Agricultural and Socio-economic droughts. The propagation of hydrological and agricultural drought originates from meteorological droughts which develop from changing phenomena within the hydrological cycle. The main droughts maybe categorized further into other types of drought.

The hydrological drought is associated with effects of deficit precipitation on surface and sub-surface water resources. Its characteristics which are defined by magnitude, severity, duration and frequency can be studied at a basin scale. Hydrological drought may be categorized into two; surface and ground water droughts. The Surface Water Drought (SWD) is caused by direct reduction in precipitation that subsequently leads to low surface runoff. The SWD is also caused indirectly by reduced groundwater discharge to surface water resources. This may be attributed to reduced flow of groundwater into surface flow in influent rivers and springs. In some instances, increase in groundwater on specific areas within a basin for an effluent river contributes to the SWD. The common indicators of SWD are reduced river flows, low water levels in reservoirs and lakes. SWD is not necessarily a naturally induced event. It may result from a combined interaction of meteorological drought, water resources development infrastructure and operational management.

On the other hand, the Groundwater Drought (GD) is a hydrological type of drought caused by significantly reduced aquifer recharge. The recharge normally takes place through permeation and inflow from sub-basins into the aquifer.¹⁴ The GD may be assessed by measuring the volumetric ground water storage. However, these data are not readily available in most river basins. Thus, aquifer level is considered to be a better indicator than the volumetric ground water storage. The GD can also be determined from the evaluation of its secondary effects such as base flow into rivers. Ground water is a vital source of water supply especially in river basins where surface water exhibits a high temporal variability with significantly low quantities. In some cases, groundwater availability is used as an indicator of relative drought risk.

The meteorological drought which is the most commonly known drought is associated with long time intervals of low or no precipitation and increased temperature. The deficiency in rainfall leads to low infiltration, decreased runoff and ground water recharge. On the other hand, high temperatures lead to changes in wind characteristics, low Relative Humidity (RH), cloud cover and increased evapo-transpiration.

Agricultural drought links meteorological or hydrological drought to agricultural impacts. Agricultural droughts impact negatively on farming systems whenever they occur. The effect of agricultural drought is normally two-fold; environmental and economic impacts. The agricultural drought is a type associated with low agricultural production, decline in output from agro-processing industries and unemployment incidents in the agricultural sector.

From the environmental view, agricultural drought is caused by insufficient precipitation, high temperature that causes elevated rates of evapo-transpiration, increased salt concentration for the crops, soil and within irrigation systems.¹⁵ The term environmental drought is sometimes used to address the adverse effects of extremely low flows on ecosystems, and may be analysed in the emerging field of eco-hydrology. The term socio-economic drought relates the supply and demand of economic goods with elements of meteorological, hydrological and agricultural drought. This drought occurs when the demand for an economic good exceeds the supply. It is caused by weather related deficit in water supply within a basin. Assessment of droughts and their forecasting is critical in formulating mitigation measures for river basins.¹⁶ Models that define probability of droughts in terms of duration, severity and return period may be developed for specific areas.⁴

Drought indices are used for assessment and characterization of droughts. These Drought Indices (DIs) were developed for specific regions using specific structures and forms of data input. There are two broad categories of drought indices; satellite based and the data driven drought indices.⁹ One of the data driven drought indices include the surface water supply index (SWSI). The SWSI was developed in for Colorado USA, as an indicator of surface water or moisture levels.¹⁷ The index requires input variables which include; snow water content, stream flow, and rainfall and storage reservoir volume. Normally the snow water content, rainfall and storage reservoir volume are used for computing the SWSI values for winter season. However, during the summer season, stream flow substitutes snow water content. At a basin scale, the SWSI values are determined from monthly catchment average values of rainfall, reservoirs, snow water content and stream flows measured at hydrometric stations within the catchment. One of the advantages of the SWSI is that it gives a representative measurement of surface water supply across the river basin.

The SWSI is unique for specific basins or regions. It requires long term record data for its calibration and thus may be limited in basins that lack sufficient data. Another limitation of the SWSI is that any additional change in the water management within a basin calls for modification of its algorithm. The change may be due addition of new water reservoirs and flow diversions that based on their effects, require to be accommodated in the algorithm.¹³ Thus, it is difficult to have a homogeneous time series of the SWSI for numerous basins.

Most basins in Kenya have limited or lack adequate quantifiable information for drought occurrence, frequency and severity. There is insufficient and scanty information of spatio-temporal drought characteristics. However, most river basins continue to experience droughts that adversely affect water resources yet their characteristics are not well understood for appropriate water resources planning and management. To prepare for effective mitigation of drought risks in a river basin, evaluation of drought characteristics is vital.

The main objective of this research was to characterize the spatial and temporal drought conditions using Surface Water Supply Index (SWSI) and detection of drought-risk areas based on hydro-meteorological data of 1970 to 2010 for upper Tana River basin in Kenya.

Description of the study area

The upper Tana River basin lies between latitudes 000 05' and 010 30' south and longitudes 360 20' and 370 60' east, with an area of 17,420 km2 Figure 1. It is part of the larger Tana River basin, the largest river system in Kenya.^18,19 It has key forest land resources located along the eastern slopes of Mount Kenya and Aberdares range. The upper Tana River basin very crucial as it influences the hydrology of the entire basin²⁰ and thus controlling the hydro-electric power generation within the Seven-Folk dams downstream. The basin is very important for hydro-electric power generation in Kenya, water supply and agricultural production.

Figure 1 The location of the upper Tana River basin in Kenya.

The elevation of the upper Tana River basin ranges from 730m to 5,190m above mean sea level (a.m.s.l.). These heights are adjacent to Kindaruma hydropower dam and at Mount Kenya respectively within the study area. The River basin exhibits heterogeneous soil types. For example, Andosols are the soil types which are predominant at high elevations, Nitosols are at the mid elevations while Ferrasols and Vertisols are at the lower elevations.¹⁸

Precipitation and temperature vary across the study area. The Mount Kenya and Aberdares ranges receive approximately annual rainfall of 1800mm.²¹ Within the mid elevation of 1200 to 1800m a.m.s.l., the annual rainfall ranges from 1000 to 1800mm while the lower elevations of 1000m, receive annual rainfall of 700mm. Although the basin receives significantly high rainfall amounts, it is characterized by seasonal rainfall fluctuations. This translates to seasonal variation of stream flow in Tana River. Generally the basin experiences bimodal rainfall pattern caused by inter-tropical convergence zone.²² The rain seasons are distributed in the months of March to June, and September to December. The precipitation is highly influenced by the orographic forces.²³ The maximum and minimum mean annual temperature vary between 25.5 to 31.00C and 21.0 to 24.00C respectively.²⁴ The average catchment evapo-transpiration is around 500mm in the summit area. Numerous land use types are found within the upper Tana River basin. The major ones include forests, crop land, and agriculture and range land. The forests and tea plantations dominate the land use activities at the high elevations of the basin.

Hydro-meteorological data

Forty years (1970-2010) monthly stream flow, precipitation (rainfall), dam inflow and dam levels from hydro-metric stations within the upper Tana River basin are used for computation of Surface water supply index (SWSI). The names and station identification numbers for meteorological and gauge stations respectively are shown on Figure 1. The data was obtained from the ministry of water environment and natural resources and water resources management authority (WRMA). The reservoir levels from Masinga dam in the basin was used in the computation of SWSI.

Surface water supply index

The input variables for the SWSI included the monthly precipitation, stream flow, storage reservoir volume, or level and dam inflow. In the present study, inclusion of the dam inflow and regression analysis was perceived to contribute to modification of the SWSI. The data was summed up and normalized using the probability of non-exceedance. This is the probability that each component is greater than the current sum as computed for each component. The determination of weighting coefficients for precipitation, stream flow, storage reservoir volume, or level, dam inflow and the ground water level in the original SWSI formulation has a weakness. The coefficients were subjectively assigned to the variables. However in this research the method is modified by an objective computation technique for the weighting coefficients and then integrating them to yield SWSI which was categorized into severity classes based on Table 1 adopted from Shafer and Dezman.¹⁷

The values of the SWSI were computed using various input parameters as shown in equation 1.

$SWSI=\frac{\left[\left(a\times P{N}_{rn}\right)+\left(b\times P{N}_{sf}\right)+\left(c\times P{N}_{rs}\right)+\left(d\times P{N}_{df}\right)-C_1\right]}{C_2}$  (1)

WhereSWSI is the surface water supply index (dimensionless), PN is probability of non-exceedence (percent), rn is the rainfall (mm), sf is stream flow(m3/s),rs is storage reservoir level components(m), df is dam inflow (m3), gr is ground water level (m). The original values of C1 and C2 for SWSI are 50 and 12 are respectively.¹⁷

Determination of weighting coefficients

The parameters a, b, c, d and e are the weights for each surface water supply index component and their sum must be equal to 1 as given in the expression:

$a+b+c+d+e=1$ (2)

The values of a, b and c were determined at different proportions contributing to the total water availability in the basin. For any monthly data series at each hydrometric station, the maximum entry of record was identified. A parameter defined as the ratio of the monthly data to the maximum entry in the period of record was computed. For instance, taking the monthly time series of precipitation data

$P_a=\frac{x_i}{x_{\max }}$ (3)

Where Pa is provisional parameter associated with a, xi is the data entry for month i and xmax is the maximum data entry of the period in record. Similarly Pb, Pc and Pd were computed as the provisional parameters for b, c, and d respectively. A total value PT was then determined by summing up the Pa, Pb, Pc and Pd. Then the parameters a, b, c and d were proportionally computed from the relations

$a=\frac{P_a}{P_T},b=\frac{P_b}{P_T},c=\frac{P_c}{P_T},d=\frac{P_d}{P_T}$ (4)

The probability of non-exceedance of monthly precipitation, stream flow, storage reservoir, dam inflow and the ground water level were computed using the relation:

$PN=1-\frac{r}{n+1}$ (5)

Where PN is probability of non-exceedence (percent), r is the rank of data arranged in ascending order and n is the number of years considered in the analysis. The integration of the rainfall (rn), stream flow (sf), storage reservoir volume (rs), dam inflow (df) and ground water level (gr) into SWSI is summarized in Figure 2A.

Normalization of the SWSI

The time series SWSI values were then normalized using the normalization Equation 6. ( Xmax=0.9; Xmin=0.1)

$X_n=X_{\min }+\frac{\left(X_o-x_{\min }\right)}{\left(x_{\max }-x_{\min }\right)}\times \left(X_{\max }-X_{\min }\right)$ (6)

Where, xn is the normalized SWSI Xmin is the minimum arbitrary value chosen based on Table 1 criterion. The Xmax and Xmin values were respective chosen as 0.9 and 0.1 since they give the best performance in the hydrological modelling as described by Morid.²⁴ From the computed monthly time series of SWSI values, drought severity was computed. Drought severity was determined as the product of the sum of SWSI values less than zero and its probability for a particular year. The probability of drought occurrence was calculated by dividing the number of months that had negative SWSI values by twelve months in a year.

Sensitivity analysis of drought indices

Sensitivity of the SWSI to input parameters was carried out prior to calibration and drought characterization. This sensitivity analysis was used to identify parameters that are fundamental in influencing the index output and in detecting and quantifying interaction effects among the parameters. The sensitivity analysis was conducted for SWSI for input parameters; precipitation, stream flow, storage reservoir volume and dam inflow and soil moisture. The procedure involved computing the mean values of each parameter and then used as the initial value. Each of the mean parameter value was altered at a rate of and the corresponding change in both the parameter and DI values determined as the difference between the new values and the previous ones. Then, the sensitivity of the DI to parameter alterations was done by computing the absolute sensitivity. This was based on the concept of the ratio of the relative change of a state variable to the relative change in parameter according to the procedure given by Jorgensen and Bendoricchio (2001) and Raude (2013). The Absolute Sensitivity relation adapted for drought in this study is defined by the relation:

$S_A=\frac{\frac{\delta D1}{D1}}{\frac{\delta P}{P}}$ (3.49)

Where;
SA = Absolute sensitivity
δDI = change in the DI value
DI = drought index value before the change
P = value of parameter being evaluated before the change δP = change in parameter value

Mann-Kendall based drought trends

The data was assessed using ordered time series. In such assessment it was considered that the sum of decrements and increments yielded a value S. The data sets were organized in form of x1, x2, x3,…,xj n-data points where xi represent data point at time j. The Mann-Kenadall statistic trend S was computed using the relation:

$S={\displaystyle \sum _{k=1}^{n-1}\left[{\displaystyle \sum _{j=k+1}^{n}sign\left(x_i-x_k\right)}\right]}$ (7)

The computation of Mann-Kendall trend procedure for the present study involved computation of sign (xi-xk), S, V(S), Z at alpha =0.05 and lastly identification of the trend based on increasing (positive value of S), decreasing (negative value of S) or no trend(zero value of S). The steps are summarized in Figure 2B.

Figure 2 The procedure for (a) SWSI computation and (b) Mann-Kendall trend test used in the study.

Spatial distribution of drought

The spatial distribution of drought was mapped using the kriging interpolation technique based on station data. This kriging method was achieved within the geo-statistical analysis tool of ArcGIS 10.1. Kriging is a reliable approach for surface interpolation of station data. The kriging interpolation technique was adopted in this research because its accuracy of has from other studies has proved to be within acceptable levels.²⁵ The kriging method may be described using the various parameters and functions that are applied in the interpolation of station values. The technique uses a parameter z*(x0) called unbiased estimator where li are chosen to satisfy the unbiased conditions and minimum variance²⁶ in which the following relation is defined:

$Z^{*}\left(x_0\right)={\displaystyle \sum _{i=1}^N{\lambda }_i\times z\left(x_i\right)}$ (8)

Then a kriging system comprising of a linear function with undefined values n+1 of the form

${\displaystyle \sum _{j=1}^N{\lambda }_i{\gamma }_{ij}+\mu ={\gamma }_{i0},i=1,...N}$  (9)

${\displaystyle \sum _{J=1}^N{\lambda }_i=1}$ (10)

Where µ is the Lagrange multiplier derived from unbiased condition. γ is the semi-variogram function which is an indicator of spatial correlation of the recognized variables. Suppose z(x) is the observed value at station x, the semi-variogram is estimated using the relation:

$\gamma \left(h\right)=\frac{1}{2N\left(h\right)}{{\displaystyle \sum _{i=1}^{N\left(h\right)}\left[Z\left(x_i\right)-Z\left(x_i+h\right)\right]}}^2$ (11)

Where N(h) is the number of observed pairs with interval distance of h by application of a matrix, the Kriging approach may be expressed as:

$Ax=b$ (12)

Where x is a vector of the unknown values, b is the right-hand side of equation 9 and A is the coefficient matrix. A, b and x are defined as:

$x=\left[{\lambda }_1{\lambda }_2...{\lambda }_N\mu \right]$ (13)
$b=\left[{\gamma }_{10}{\gamma }_{20}...{\gamma }_{N0}1\right]$ (14)
$A=\left[\begin{array}{cccc}{\gamma }_{11}& {\gamma }_{21}& {\gamma }_{N1}& 1\\ {\gamma }_{12}& {\gamma }_{22}& {\gamma }_{N2}& 1\\ :& :& :& 1\\ \begin{array}{l}{\gamma }_{1N}\\ 1\end{array}& \begin{array}{l}{\gamma }_{2N}\\ 1\end{array}& \begin{array}{l}{\gamma }_{NN}\\ 1\end{array}& \begin{array}{l}1\\ 0\end{array}\end{array}\right]$ (15)

In the present study, the hydrometric stations within and adjacent to the upper Tana River basin were used for hydrological evaluation. These stations have unique geographical location and to capture spatial extend of the stations, Geographical Information System (GIS) was applied. GIS provides effective analysis of spatial distribution of hydro-meteorological data and enhances hydrological modeling. For this research, GIS was used to compute and illustrate the spatial distribution, variation and trends of droughts based on SWSI. The spatial extrapolation was achieved at a confidence interval of 95% (Alpha=0.05, critical value 1.645) Figure 3.

Figure 3 The time series of SWSI for at (a) Yatta furrow (b) Nyamindi (c) Tana sagana and (d) Amboni gauge stations.

Development and modification of SWSI equation

The weighting parameters a, b, c and d corresponding to the rainfall, stream flow, reservoir levels and dam inflows were estimated through a proportioning objective procedure. The product of the respective time series weight parameters and the probability of non-exceededance were computed to get composite factor SWSIf and the then the SWSIf normalized using the Equation 4 to get the SWSI. A regression plot between SWSIf and SWSI was them done to get the SWSI Equation which is further simplified for upper Tana River basin. For instance for Kamburu gauge station the following relation for modified SWSI was obtained at regression coefficient of R2 of 0.8626:

$SWS{I}_m=\frac{\left[2.04\times \left(a\times P{N}_{rn}+b\times P{N}_{sf}+c\times P{N}_{rs}+d\times P{N}_{df}\right)-1\right]}{0.1849}$ (16)

Where SWSIm is the modified surface water supply index, 2.04, 1 and 0.1849 are conceptual parameters that depend upon the basin characteristics.

Drought based on the modified SWSI time series

Based on Equation 6, the drought occurrence in the upper Tana River basin was computed using the SWSI monthly time series. To illustrate the time series SWSI, and the average monthly rainfall at each hydrometric station, the results of four gauge stations are summarized in Figure 4.

Figure 4 Sensitivity of SWSI to decrease in weighted parameters.

Figure 4.1 Sensitivity of SWSI to increase in weighted parameters.

Figure 4.2 The spatial distribution of drought severity (a-e) for the period 1970-2010, drought frequency (f), Mann-Kendall trend test (g) and rainfall (h) for the upper Tana River basin.

Sensitivity of SWSI to weighting parameters

The results of the absolute sensitivity analysis show that different weighting parameters of SWSI influence the index output at varying magnitudes. The results show that the sensitivity of SWSI to the four main weighting parameters increased in the order of c, b, d and a. This means thatthe ascending order of SWSI sensitivity to parameter change is reservoir level, stream flow, dam inflow, and precipitation and reservoir levels respectively. The SWSI was found to be most sensitive when weighting variables related to precipitation (a) was decreased. On the other hand, the SWSI was least sensitive to both decrease and increase in reservoir levels (c). Generally, the SWSI was found to be more sensitive to a decrease than an increase in the weighted parameter values as given in Figure 4.1. The SWSI high sensitivity of weighting parameter a is attributed to the fact that precipitation is the most significant hydrological component that contributes to the runoff and the stream flow Figure 4.2. Quantifying the SWSI sensitivity to parameter changes helped to understand its response to errors in parameter estimation prior to model calibration.

It was observed that the drought severity varied from station to station with major droughts of different durations occurring between the years 1990 to 1997 for all the gauge stations. During such a period, the SWSI values were consistently below -3.0 in all the stations. This means that most areas in the basin experienced severe drought in the stated years. Other years when the stations experienced droughts at varying magnitudes as detected by the SWSI include 1973 and 1978 when the SWSI values were at or below -3.0.

Spatial distribution of drought

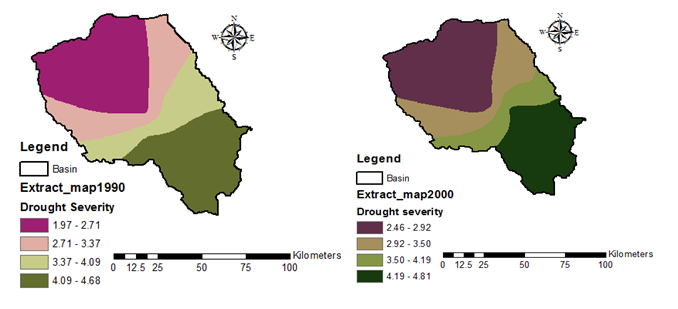
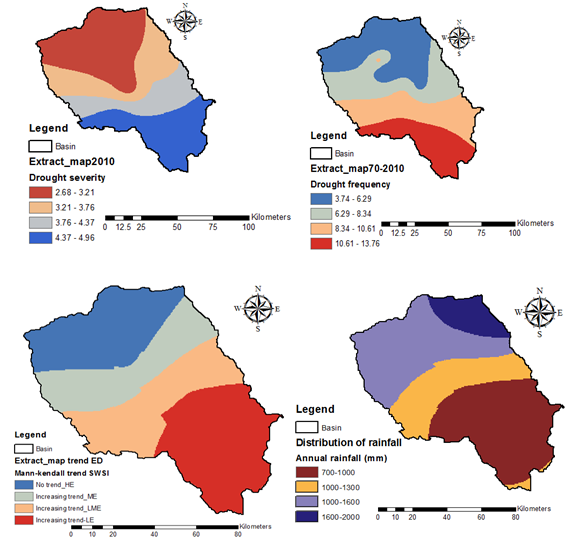
Drought severities at 10 year interval; 1970, 1980, 1990, 2000 and 2010 were computed to detect any variations across the basin over the years. The results show that the drought severity has been increasing over the years with values of between 1.69-2.22 and 3.59-4.17 Figure 4A for 1970 and 3.74-6.29 and 4.37-4.96 Figure 4E for 2010. Generally the areas in south-east parts of the basin have the highest drought severity over all the years. These areas are located within the ASALs at low elevations and receive annual average precipitation of between 700 and 1000 mm. Figure 4H. These south-eastern areas exhibit the highest decadal drought severities are considered to be the most drought-risk prone areas. The areas north-west of the basin exhibit low drought severities and are within humid zones at high elevations with precipitation range from 1000 to 2000mm Figure 4H. Areas that are at high risk of drought occurrence at different time scales are identified on the bases of drought frequency. The drought frequency was computed as a ratio of the drought occurrence in each time interval to the total drought occurrence of same drought class.²⁷ In terms of severity area coverage of the basin, there is a significant increase in area under high drought severity from 1970 to 1990 for the areas in the south-eastern parts of upper Tana River basin. However, the area experiencing high drought severity generally does not have a significant change from 1990 to 2010. On the other hand, areal coverage of low drought did not significantly change in the north-west parts of the basin over the years Figure 4.

For the purpose of illustrating the drought frequency the extreme drought (ED) is illustrated in Figure 4G. The frequency shows that the areas in southern parts of the basin are most prone to extreme drought with highest drought frequency of between10.61-13.76 at southern areas and northern parts exhibit lowest frequency of 3.74-6.29 Figure 4F.

Generally, drought events have significantly changed in most parts of the basin for the period 1970-2010. With the areas in the south-eastern that is the ASALs are most prone to droughts than all the other areas. The drought trend may is attributed to global climate change and variability, land temperature in most parts of the world which have been increasing leading to change in precipitation.

Drought has been projected to increase in future in the upper Tana River basin due to global climate change. This study reveals that the south-eastern parts of the basin located in the ASALs is most prone to the droughts, and are thus the most drought-risk areas across the basin over the 40 years of study. Since it is not possible to alter the natural causes of drought, the results can be incorporated in early warning systems that involve collaboration of all stakeholders; government development and planning departments, institutions. The major output of the present study is the generation of drought severity or risk maps which can be applied by the water resources stakeholders of the basin such as disaster management, hydropower generation and distribution, agricultural organizations, farming communities and development authorities.

A more detailed research which is in progress on the drought forecasting capability of different models in conjunction with SWSI at different lead times within the basin for improved drought preparedness is paramount.

The authors acknowledge the Egerton University, Division of Research and Extension for support in publishing of articles from a broad drought assessment and forecasting research.

The author declares no conflict of interest.

1. Liu X, Wang S, Zhou Y, et al. Regionalization and spatiotemporal variation of drought in China based on standardized precipitation evapotranspiration index (1961–2013). Advances in meteorology. 2015;2015:1–18.
2. Van–loon AF, Laaha G. Hydrological drought severity explained by climate and catchment characteristics. Journal of hydrology. 2015;526(2015):3–14.
3. UNDP. Kenya: adapting to climate variability in Arid and Semi–Arid Lands (KACCAL), project report. In: Wilby RL, editor. Risks posed by climate variability to delivery of water framework directive objectives. Environ Int in press; 2012.
4. Shatanawi K, Rahbeh M, Shatanawi M. Characterizing, monitoring and forecasting of drought in Jordan river basin. Journal of water resources and protection. 2013;5:1192–1202.
5. Asgari H, Mohsenipour M, Shahid S, et al. Spatio–temporal characteristics of droughts and trends in Qazvin province of Iran. Research Journal of Applied sciences. 2014;8(11):1299–1311.
6. Wang XJ, Zhang JY, Shahid S, et al. Water resources management strategy for adaptation to droughts in China. Mitigation and adaptation strategies global change. 2012;17(8):923–937.
7. Vicente–Serrano SM, Lopez–moreno JL, Begueria, S, et al. Accurate computation of stream flow drought index. Journal of hydrologic Engineering. 2012;17(2):318–332.
8. Karamouz M, Rasouli K, Nazi S. Development of a hybrid index for drought prediction: case study. Journal of Hydrologic Engineering. 2009;14(6):617–627.
9. Belayneh A, Adamowski J. Drought forecasting using new machine learning methods. Journal of Water and Land Development. 2013;18(I–IV):3–12.
10. Sharma TC. A drought frequency formula. Hydrological sciences journal. 1997;42(6):803–814.
11. Kyambia MM, Mutua BM. Analysis of drought effect on annual stream flows of river Malewa in the L. Naivasha basin, Kenya. IJCRR. 2014;6(18):1–6.
12. Zoljoodi M, Didevarasl A. Evaluation of Spatio–temporal variability of droughts in Iran using Palmer Drought Severity Index and its precipitation factors through (1951–2005). Atmosphere and Climate Sciences Journal. 2013;3:193–207.
13. Barua S. Drought assessment and forecasting using a non–linear aggregated drought index. Australia: PhD thesis, Victoria University; 2010.
14. Adindu R, Igboekwe M, Isu JO, et al. Estimation of groundwater recharge at Amudike watershed, Abia State Nigeria. European Journal of applied engineering and scientific research. 2013;2(3):38–43.
15. Mishra AK, Singh VP. A Review of Drought Concepts. Journal of Hydrology. 2010;391(1–2):202–216.
16. Sharda V, Srivasta P, Kalin L, et al. Development of community water deficit index (CWDI) –Drought forecasting tool for small to mid–size communities of south eastern United States. Journal of Hydrologic Engineering. 2012;18(7):846–858.
17. Shafer BA, Desman LE. Development of a Surface Water Supply Index (SWSI) to assess drought conditions in snowpack Runoff Areas, proceedings of the Western snow conference Reno. Nevada, USA; 1982. p. 164–175.
18. Jacobs J, Angerer J, Vitale J, et al. Exploring the Potential Impact of Restoration on Hydrology of the Upper Tana River Catchment and Masinga Dam, Kenya, a Draft Report. Texas A & M University; 2004.
19. WRMA. Physiological survey in the upper Tana catchment, a natural resources management project report. Nairobi; 2010.
20. IFAD. Upper Tana catchment natural resource management project report, east and southern Africa division, project management department. 2012.  
21. Otieno FAO, Maingi S M. Sedimentation problems of Masinga reservoir. In land and water management in Kenya. In: Gichuki FN, et al. editors. Kenya: published by Soil and Water Conservation branch of Ministry of Agriculture and Rural development; 2000.
22. Wilschut LI. Land use in the upper Tana: Technical report of a remote sensing based land use map. In green water credits report 9. In: Mcmillan B, et al. editors. ISRIC–world soil information. 2010.
23. Saenyi WW. Sediment management in Masinga reservoir, Kenya. Vienna Austria: PhD thesis (Published), University of Agricultural Sciences (BOKU); 2002.
24. Mutua BM, Klik A. Predicting daily stream flow in un–gauged rural catchments; the case of upper Tana River basin, Kenya. Journal of spatial hydrology. 2007;5(2):64–80.
25. Robinson TP, Matheernnicht G. Testing the performance of spatial interpolation techniques for mapping of soil properties. Journal of computers and electronics in agriculture. 2006;50(2006):97–108.
26. Kim TW, Valdes JB. Frequency and spatial characteristics of droughts in the Conchos River Basin, Mexico. International water resources association journal. 2002;27(3):420–430.
27. Mckee TB, Doesken NJ, Kleist J. The relationship of drought frequency and duration to time scales. In 18th conference on applied climatology California. USA; 1993. p. 179–184.