A novel method is developed for riprap design of scour protection at bridge piers. The method is based on the assumption that the minimum stable riprap size exists when the work done due to the attacking vertical flow jet upstream of the bridge pier is no longer capable to lift the protecting riprap particles out of the scour hole. The developed equation expresses the minimum particle size as a function of the longitudinal velocity just upstream of the pier, the flow depth, the bed material/riprap specific gravity, and the pier width. The proposed equation has the advantages that it is theoretically based which allows adding wave and seismic forces in addition to the already considered hydrodynamic forces, it includes effects of pier width, it determines bed armoring, and it gives the equilibrium minimum riprap size while previous methods give the median size D50.

Keywords: riprap design, bridge piers, mathematical modeling, scour holes, energy transfer/balance theory, bed armoring, wave forces, seismic forces

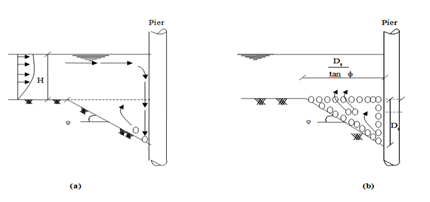
Bridges are important means for transporting people and goods across waterways. Such important structures usually cost millions of Dollars. Unfortunately, bridges are subjected to scour especially during floods due to the scouring action of the attacking flow upstream of the bridge. The upstream horizontal flow, after hitting a bridge pier, is converted to a vertical downward jet that attacks the bed material surrounding the bridge pier and starts the scouring mechanism.^1,2 The developed horseshoe and wake vortices help in the continual removal of the bed material further downstream. Scour could be so severe to the point of undermining the bridge foundation leading to its collapse. To protect against scour, riprap has been the most commonly used pier scour countermeasure.^3,4 Riprap often consists of large stones placed around a pier to armor the bed by preventing the down flow jet from entraining the underlying bed sediments and thus preventing the formation of a scour hole. The size of the stone riprap, which is the focus of this study, is the most critical factor for determining the stability of the riprap layer.

There have been a large number of formulas for determining the size of the riprap stones all of which are in terms of the median particle diameter D₅₀. Table 1 lists most of the existing riprap sizing formulas reduced to a common form for comparison, according to Lagasse et al.,⁴ Melville et al.⁵ The range for the exponents of Froude number appearing in these formulas is between 2 to 3 except for Lauchlan⁶ equation which has a small exponent of 1.2 indicating a nearly linear variation. Comparison of the different equations,^3,4 reveals a wide gap in their predictions for a range of Froude numbers between 0.2 to 0.6 with coefficients for round–nose pier and sediment specific gravity of 2.65. The lack of consistency among the methods led Melville et al.⁵ to recommend the use of Lauchlan,⁶ Richardson et al.⁷ methods for sizing riprap for bridge pier protection because they lead to conservatively large riprap relative to the other methods. Karimaee et al.⁸ attribute the difference between the various equations to different ranges of relative riprap size (pier width/median riprap size). The existing riprap sizing equations are based on either threshold of motion criteria or empirical results of small–scale laboratory studies conducted under clear–water conditions with steady uniform flow.⁴ They report that past practices have been to size riprap such that no movement of the material would occur at the design velocity, which has led to over–sizing of riprap due to difficulty in adjusting precisely the hydraulic loads. Due to differences and non–clarity of the definition of failure, the experimental studies vary widely which may put some doubt on the accuracy of their equations. For example, Chiew et al.⁹ increased flow velocity in increments until the ratio of scour depth experienced by riprap layer to maximum scour depth of the unprotected sediment bed is 1.0. Croad¹⁰ took critical conditions when riprap layer completely disintegrates. Quazi et al.¹¹ defined failure as occurring when any grain or grains were dislodged from front half of layer close to pier face. Parola^12,13 installed three layers thick with middle layer painted fluorescent orange and defined failure as exposure of these orange stones without removal of them over 30 min period. Lauchlan⁶ defined failure occurring when the local scour depth at a riprap–protected pier exceeds 20% of the scour depth at the unprotected pier. Karimaee et al.⁸ fixed the tail water depth for 15 min, and if riprap did not move, the depth was increased gradually by approximately 5 mm and the experiment continued for another 15 min. This procedure continued until instability (shear failure) in the riprap was observed. They considered the movement of a few riprap stones in 15 min as the failure criterion because it leads eventually to movement of more and more stones. The above scour types are shear failure where the riprap layers are entrained by the flow. For other types of riprap failure, Chiew¹⁴ discussed winnowing and edge failures for clear water conditions while Chiew et al.⁹ discussed bed–form undermining scour for live bed conditions. Lagasse et al.⁴ discussed how stone size influences winnowing, edge failure and bed form destabilization. Still, shear failure is the most addressed type of failure due to its high likelihood and will be dealt with in this study.

Froehlich¹⁵ presents an expression for sizing loose rock riprap placed around bridge piers which was derived based on an evaluation of moments that resist and promote overturning of a single rock particle, on an elementary potential flow theory which provides models of velocities around piers of various cross–sectional shapes, and on empirical relations and coefficients used to calculate shear stresses acting on rock riprap and the critical values of shear stress at which rock is moved. However, it took about 30 equations/formulas and several graphical relationships to find the minimum diameters of stable rock riprap given by the analytical relation for circular columns. Theoretical shape factors, which are multiplied times the stable rock size needed for a circular column of the same width, were found for piers having square ends and for piers having sharp ends with interior nose angles of 60°, 90°, and 120°. A safety factor that provides a suitable margin of error needed for design is found by comparing calculated and measured rock sizes for both round–nosed and square–nosed pier experimental data. Froehlich¹⁵ assumed a value of the Shields parameter of 0.06. Karimaee et al.⁸ presented equation, based on 140 sets of experiments, in which stability of riprap (stability number) depends on the relative stone size, relative flow depth and the relative pier effective width. However, the stone median size appears on both sides of their equation which requires trial and error approach for calculating the riprap stone size. Karimaee et al.¹⁶ used large data set of at 264 experiments available in the literature. Based on at least 190 experiments the effective pier width was found to be the most effective parameter on riprap stability. They presented an empirical relationship (based on multiple regression analysis) between the flow intensity$\text{V/}{\text{V}}_{\text{c}}$ and the relative stone size and the relative pier effective width where V is the flow velocity and ${\text{V}}_{\text{c}}$is the critical velocity for riprap stone movement. Trial and error approach is required in order to determine the stable riprap stone size. This approach can be considered as a modification of that by Chiew¹⁴ who considered $\text{V/}{\text{V}}_{\text{c}}\text{ < 0}\text{.3}$as stability condition. They considered $\text{V/}{\text{V}}_{\text{c}}\text{=035}$ divided by two modification factors for the relative pier width and relative stone size. The ratio of the predicted riprap sizes by the developed empirical equation to experimental sizes had an average value of 1.7. Using artificial neural network model provides around 7% improved prediction for riprap size compared to the conventional regression formula. Mashahir et al.¹⁷ used similar approach in which they took $\text{V/}{\text{V}}_{\text{c}}\text{=0}\text{.30}$but with different modification factors.

Other aspects of riprap design such as extent of riprap for piers with or without collars was investigated by Karimaee et al.¹⁸ Their experiments showed that in case of aligned rectangular pier without a collar only 8% of the area around the pier is critical and in case of protected pier with collar, the collar prevents the critical region around the pier in aligned and 5o skewed piers. The effect of collar on a pier located in 180–degree river bend was investigated by Nohani et al.¹⁹ where the experiments showed that the relative rock size significantly affected the stability number for cylindrical piers. Also, they found that greater collars were more effective than smaller collars on increasing the stability. Lauchlan et al.³ investigated the depth of placement of the riprap layer. The present study aims at examining theoretically the sizing of riprap stones to protect bridge piers from scour due to shear failure using a novel theoretical method. The novel theoretical method is based on the fact that the minimum stable riprap size exists at condition when the work done due to the attacking vertical flow jet upstream of the bridge pier is no longer capable to lift the riprap particles out of the scour hole. By applying the theoretically developed riprap sizing equation and the existing equations to laboratory data, it is hoped that this will shed more light on the performance of the riprap sizing equations. The theoretical foundation of the presented approach offers extra advantages which include clarity of defining riprap failure, and the possibility of inclusion for riprap design of protection against scour due to other forces such as wave forces (due to wind and ship movement) and seismic forces.

The present approach

The work transfer theory which dealt with turbulent wall jets by Hafez² or its synonym the energy balance theory by Hafez^20,21 which dealt with bridge pier scour; treated the whole scour hole as occupied by a one–mega sediment particle having the shape of the scour hole. Due to that, the bed sediment size did not appear explicitly in these approaches and sediment size effects were reflected merely through its connection to the angle of repose. However, the development made here is based on consideration of a single bed particle which results in explicit appearance of bed sediment/riprap particle size.

The basic assumptions needed herein are that:

1. Steady uniform flow conditions;
2. The bed particles are spherical in shape and can be natural bed sediments or riprap particles. Almost all studies in sediment transport treat the bed particles as spheres with the median diameter as the characteristic length scale. The spherical assumption made here is just to simplify the calculations but other shapes scan be used if the ratio of the particle volume to its horizontal projected area is known;
3. The size of bed particles is relatively small compared to the scour depth
4. The horizontal water–flow upstream of the bridge pier consists of thin water tubes in accordance with Hafez.²¹ The water surface tube will hit the bridge pier, then bends downward while being attached to the pier surface. It starts to erode the first bed surface particle next to the pier, i.e. assuming the tube diameter is equal to the bed particle diameter. Bed erosion continues with each new bed surface particle being eroded and removed upward by the flow horse–shoe vortices. The other tubes below the surface tube will bend down and distribute themselves all over the length of the scour hole thus attacking the bed particles. By the end of the scour process and with formation of the scour hole its deepest point will be located just next to the pier with scour depth as Ds. The deflected water surface tube has then traveled a distance equal to the upstream water depth, H, plus a distance equals to Ds which is the maximum scour depth, Figure 1A; and
5. At or after equilibrium conditions, the work done due to the attacking flow jet is less than the work needed to lift upward out of the scour hole the sediment/riprap particles located at the deepest point of the scour hole.

This last statement defines the stable sediment/riprap size as that size for which no movement or entrainment by the flow forces occurs. Past methods connected the no movement criteria to the median size D50 and not to the minimum size as done here. If D50 is determined as connected to the no movement criteria in past methods, particles smaller than D50 will be less stable and will tend to move and this will cause unwanted scour or winnowing effect. Therefore the use of D50 in past methods can have some deficiency. Now the derivation of the novel theoretical equation is given. Basic fluid mechanics teaches, Roberson et al.²² that the flow hydrodynamic momentum force for steady uniform flow conditions, can be expressed as $\text{ρ} \text{Q} \text{V}$ or equivalently

$\rho {\text{V}}_{{}_{\text{Z}}}{}^{\text{2}}{\text{A}}_{\text{p}}$

Where
$\rho$is the fluid density,
Q is the flow discharge,
V is the flow velocity and
A is the normal cross–sectional area to flow.

As in assumption (4), the water surface tube upon hitting the bridge pier and travelling downward with a velocity VZ, will hit a bed material particle with diameter, d, which is located at the deepest point of the scour hole just in front of the pier. This force will act on a projected area,${\text{A}}_{\text{p}}$ of the bed material particle where ${\text{A}}_{\text{p}}\text{=π}{\text{d}}_{\text{2}}\text{/4}$(spherical particles have circular projected areas) and d is the bed particle diameter. The force of this vertical jet on this bed particle is then given as$\text{ρ}{\text{V}}_{\text{z}}{}^{\text{2}}{\text{A}}_{\text{p}}$. Not all of the projected area of the particle is exposed to the vertical jet as the particle maybe sheltered by other particles. In addition, not all of the attacking flow–jet energy is transferred to the bed particle. A factor$\text{λ}\left(\text{λ}\le \text{1}\text{.0}\right)$ is therefore used to denote both of the effective projected area and the efficiency of transfer of energy from the flow jet to bed particles. The force $\text{ρ}{\text{V}}_{\text{z}}{}^{\text{2}}{\text{A}}_{\text{p}}$ acting on a bed particle travels a maximum vertical downward distance equal to $\left(\text{H+ Ds}\right)$The work done by gravity on this falling down vertical jet is therefore$\rho {\left({\text{V}}_{\text{Z}}\right)}^{\text{2}}{\text{A}}_{\text{p}}\left(\text{H+ D}{}_{\text{s}}\right)$. The work transferred to the bed particle located in the deepest point of the scour hole is$\lambda \rho {\left({\text{V}}_{\text{Z}}\right)}^{\text{2}}{\text{A}}_{\text{p}}\left(\text{H+ }{\text{D}}_{\text{s}}\right)$.

The entertainment of sediment particles from a pier scour hole does not travel directly straight upwards during the scour process because the horseshoe vortices sweep them down to the scour hole and then move them upward in the downstream direction. However, as far as the work done against gravity to move these sediment particles only the upward distance is of the concern here. The work needed in moving the bed particle at the deepest point of the scour hole in front of the pier out of the scour hole up to the original bed level is equal to the particle submerged weight times the maximum upward travelled distance which is (Ds + d/2). When the bed particle reaches the original bed level it will be picked up by the horseshoe vortices and will be moved further downstream. The energy of the horse shoe vortices is coming from the mean turbulent flow fluctuations as explained by Hafez.²¹ Therefore, the work needed to lift a particle out of the scour hole is given as

$\text{(}{\gamma }_{\text{s }}\text{– }\gamma \text{) }\left(\text{Vol}\right)\left(\text{D}{}_{\text{s}}\text{+ d/2}\right)$

Where,
${\text{γ}}_{\text{s}}$ and$\text{γ}$  are the unit weights of the bed particle and water respectively, and
Vol is the volume of the sediment/riprap particle

If d ˂˂ Ds, as stated in assumption (3) above, then this work becomes$\left({\gamma }_{\text{s}}\text{ – }\gamma \right)\left(\text{Vol}\right)\left({\text{D}}_{\text{s}}\right)$. Assumption (5) above states that at or after equilibrium conditions, the maximum work done due to the attacking flow jet is less than the work needed to lift the sediment/riprap particles upward out of the scour hole. This statement can be expressed mathematically as:

$\lambda \rho {\text{V}}_{\text{z}}{}^{\text{2}}\text{(}{\text{A}}_{\text{p}}\text{)}\text{(H}\text{+}{\text{D}}_{\text{s}}\text{)}\le \text{(}{\gamma }_{\text{s}}\text{-}\gamma \text{)}\text{(Vol)}{\text{D}}_{\text{s}}$(1)

Dividing inequality (1) by H, while assuming that H ≠ 0, yields

$\lambda \rho {\text{V}}_{\text{z}}{}^{\text{2}}\text{(A}{}_{\text{p}}\text{)}\text{(1}\text{+}\frac{{\text{D}}_{\text{s}}}{\text{H}}\text{)}\le \text{(}{\gamma }_{\text{s}}\text{-}\gamma \text{)}\text{(Vol)}\text{(}\frac{{\text{D}}_{\text{s}}}{\text{H}}\text{)}$(2)

Solving for Ds/H in inequality (2) results in

$\frac{{\text{D}}_{\text{s}}}{\text{H}}\ge \frac{\lambda \rho {\text{V}}_{\text{z}}{}^{\text{2}}}{\text{(}{\gamma }_{\text{s}}\text{-}\gamma \text{)}\text{(}\frac{\text{Vol}}{{\text{A}}_{\text{p}}}\text{)}\text{-}\lambda \rho {\text{V}}_{\text{z}}{}^{\text{2}}}$(3)

Multiplying inequality (3) by H/b, where b is the pier width and assuming that b ≠ 0, yields

$\frac{{\text{D}}_{\text{s}}}{\text{b}}\ge \frac{\lambda \rho {\text{V}}_{\text{z}}{}^{\text{2}}\text{}\text{}\text{(}\frac{\text{H}}{\text{b}}\text{)}}{\text{(}{\gamma }_{\text{s}}\text{-}\gamma \text{)}\text{(}\frac{\text{Vol}}{{\text{A}}_{\text{p}}}\text{)-}\lambda \rho {\text{V}}_{\text{z}}{}^{\text{2}}}$(4)

In line with Raudkivi 23 it is assumed that${\text{D}}_{\text{s}}\text{/b }\le {\text{C}}_{\text{max}}$

Where,
${\text{C}}_{\text{max}}\approx \text{2}\text{.3 K}\alpha$and
$\text{K}\alpha$is a pier shape coefficient.

This relation defines the upper limit for the dimensionless scour depth. It should be noted that the scour depth, Ds, can be considered to be resulting from the combination of the local pier scour, contraction scour and general scour.

Combining inequality (4) and Raudkivi’s²³ condition yield

$\frac{\lambda \rho {\text{V}}_{\text{z}}{}^{\text{2}}\text{}\text{}\text{(}\frac{\text{H}}{\text{b}}\text{)}}{\text{(}{\gamma }_{\text{s}}\text{-}\gamma \text{)}\text{(}\frac{\text{Vol}}{{\text{A}}_{\text{p}}}\text{)-}\lambda \rho {\text{V}}_{\text{z}}{}^{\text{2}}}\le \frac{{\text{D}}_{\text{s}}}{\text{b}}\le {\text{C}}_{\text{max}}$ (5)

Inequality (5) can be expressed as:

$\frac{\lambda \rho V_z{}^2\text{}\text{}(\frac{H}{b})}{({\gamma }_s-\gamma )(\frac{Vol}{A_p})-\gamma \rho V_z{}^2}\le C_{max}$  (6)

Solving inequality (6) for $\left(\text{Vol/}{\text{A}}_{\text{p}}\right)$ results in:

$(\frac{Vol}{A_p})\ge \frac{\lambda \rho V_z{}^2\text{}\text{}(1+\frac{H}{C_{max}b})}{({\gamma }_s-\gamma )}$ (7)

For spherical particles, $\left(Vol/A_p\right)=\left(\pi d_3/6\right)/\left(\pi d_2/4\right)=\left(4/6\right)d$

Where d is the diameter of a sphere. Inequality (7) can be put in an equation form when d is understood to be the minimum grain size at which the scour hole is stable or at equilibrium under the given flow hydrodynamic conditions.

Taking $d=d_{min}$

Where dmin is the minimum stable or equilibrium particle/riprap size and substituting (4/6) d for $\left(\text{Vol/}{\text{A}}_{\text{p}}\right)$ in inequality (7) yields:

$d_{min}=\frac{1.5\lambda \rho V_z{}^2\text{}\text{}(1+\frac{H}{C_{max}b})}{({\gamma }_s-\gamma )}$(8)

For cube particles or brick particles with length and width twice the height (Vol/Ap) = d. If this were used in Inequality (7), the factor 1.5 appearing in Eq. (8) would be 1.0; thus yielding less riprap size. Therefore, using riprap sizes calculated on the assumption of spherical particles is on the safe size Further, the vertical velocity just upstream of the pier appearing in the above equation can be assumed as first approximation as a related to the average main stream longitudinal velocity, ${\text{V}}_{\text{x}}$,via: ${\text{V}}_{\text{z}}\text{ = }{\text{C}}_{\text{v}}{\text{V}}_{\text{x}}$. Substituting this in Eq. (8) yields:

$d_{min}=\frac{1.5\lambda \rho C_v^2{V}_x{}^2\text{}\text{}(1+\frac{H}{C_{max}b})}{({\gamma }_s-\gamma )}$  (9)

Equation (9) can be further simplified to:

$d_{min}=\frac{1.5\lambda C_v^2{V}_x{}^2\text{}\text{}(1+\frac{H}{C_{max}b})}{g(S_s-1)}$  (10)

Where g is gravitational acceleration and Ss is the bed particles’ specific gravity.

Eq. (10) indicates that riprap size needed for scour protection increases with increases in approach velocity, approach water depth and decreases with increase in riprap particles specific gravity. In addition, the increase in scour–depth reduces the required riprap size due to the increase in dissipation of the flow energy due to the formation of the scour hole. Equation (10) does not indicate that the riprap size increases indefinitely with the approach flow depth, H, as when H increases the velocity ${\text{V}}_{\text{x}}$ decreases accordingly. Since velocity varies quadratically while H varies linearly in Eq. (10), then ${\text{V}}_{\text{x}}{}^{\text{2}}$ vanishes faster than the increase in H and therefore

the combination ${\text{V}}_{\text{x}}{}^{\text{2}}\text{ H}$ diminishes for very large value of H. Equation (10), when the bed material sediments are considered without being covered by riprap, can provide the minimum bed material size under bed–armoring conditions. If the riprap particles are greater than the minimum bed material size, which is given by Eq. (10), then no scour is expected and the riprap layer is stable under the same flow conditions.

Dividing Eq. (10) by H and using ${\text{F}}_{\text{r}}\text{ = }{\text{V}}_{\text{x}}{}^{\text{2}}\text{/ }\left(\text{g H }\right)\text{0}\text{.5}$ where Fr is the Froude number yields

$\frac{d_{min}}{H}=\frac{1.5\lambda C_v^2{F}_r^{{}^2}\text{}\text{}(1+\frac{H}{C_{max}b})}{(S_s-1)}$  (11)

Graf et al.24 report${\text{V}}_{\text{z}}\text{ = 0}\text{.6 V}$, and Raudkivi²³ reports for circular piers that the maximum velocity of the down flow reaches 0.8 times the mean approach velocity. However these values are at higher elevations than at the point of the deepest level of the scour hole. It is assumed here that ${\text{C}}_{\text{v}}$ at just above the point of the deepest level of the scour hole is about 0.5 which is an average between the maximum velocity (V) at the surface and zero velocity at the bed. Of course, detailed hydrodynamic flow models can provide better estimation of ${\text{V}}_{\text{z}}$ near the bed. Assuming that almost all of the energy in the attacking flow jet is transferred to the bed particle, will lead to be in the safe side. In addition, for more safety it can be assumed that the exposed area of the bed particle is at maximum. The last two assumptions lead to λ ≈ 1.0. With ${\text{C}}_{\text{v}}$ = 0.5 and$\text{λ}$ = 1.0, Eq. (11) becomes:

$\frac{{\text{d}}_{\text{min}}}{\text{H}}\text{=}\frac{\text{0}\text{.375}{\text{F}}_{\text{r}}^{{}^{\text{2}}}\text{}\text{}}{\text{(}{\text{S}}_{\text{s}}\text{-}\text{1)}}\text{(1}\text{+}\frac{\text{H}}{{\text{C}}_{\text{max}}\text{b}}\text{)}$ (12)

It is interesting to note that Eq. (12) which is derived theoretically has the same form as the existing laboratory based equations in Table 1 but with the addition of pier width and flow depth. The importance of these two factors was addressed by Karimaee et al.⁸ It should be noted that effects of pier shape, sediment gradation, flow inclination, riprap placement depth, etc. can be accommodated when using Eq. (12) using the traditional adjustment or correction coefficients listed in the literature as multipliers in the right hand side of Eq.(12) . By selecting a suitable value for ${\text{C}}_{\text{max}}$ (say ${\text{C}}_{\text{max}}\text{ b = 0}\text{.2 Ds}$ of the unprotected pier) it can represent the 20% scour criteria proposed by Lauchlan.⁶ Eq. (12) indicates that in order to have a very small scour depth (say in the order of few centimeters) the bed material particles are supposed to have a very large size. In the limit if the scour depth is thought to be zero, an infinite bed material size would be needed under the assumption of excess of critical conditions (assuming the velocity (Vx) in Eq. (10) is V–Vc.

The rearranged Isbash²⁵ equation²⁶

${\text{D}}_{\text{50}\text{.}}\text{=}\frac{\text{0}\text{.692}{\text{(}{\text{V}}_{\text{des}}\text{)}}^{\text{2}}}{\text{(}{\text{S}}_{\text{s}}\text{-}\text{1)}\text{2}\text{g}}\text{=}\frac{\text{0}\text{.346}{\text{(}{\text{V}}_{\text{des}}\text{)}}^{\text{2}}}{\text{(}{\text{S}}_{\text{s}}\text{-}\text{1)}\text{g}}$ (13)

Where ${\text{V}}_{\text{des}}$ is the design velocity for local conditions at the pier. Eq. (13), if ${\text{V}}_{\text{des}}$ is taken as the upstream velocity, can be written as:

$\frac{{\text{D}}_{\text{50}\text{.}}}{\text{H}}\text{=}\frac{\text{0}\text{.346}{\text{F}}_{\text{r}}{}^{\text{2}}}{\text{(}{\text{S}}_{\text{s}}\text{-}\text{1)}}$   (14)

Eq. (14) is very similar to the equation of Richardson et al.⁷ Comparison of equations (12) and (14) reveals remarkable similarity between the first which is based on theoretical consideration and the second which is based on laboratory data.

Experimental data collected in small–scale laboratory channels by Quazi et al.¹¹ and Parola¹³ which are shown in Table 2, are used to test the developed riprap sizing equation, Eq. (12) and the existing formulas in Table 1. As reported by Froehlich¹⁵ the laboratory channels in these experiments all had constant rectangular cross section with solid beds. The riprap was modeled using crushed, angular gravel placed in horizontal layers that surrounded the model piers completely. Froehlich¹⁵ states that although differences in thickness and lateral extent of the riprap layers, and the duration of experiments, leads to some inconsistencies between data, the assemblage comprises a valid and useful means of testing the theoretical formulations that are developed and for comparing results of expressions developed by others for sizing loose rock riprap to protect bridge piers. Froehlich¹⁵ further states that all of the experiments were carried out by increasing of hydraulic loads by small amounts until failure of riprap occurred; that is riprap displacement. Because of the incremental increases, there were possibilities that the applied load might be larger than the failure load. However, presumably the researchers made sure that their load increments were small to minimize such differences Froehlich.¹⁵

Applications to laboratory data

In applying Eq. (12) to the data in Table 2, it will be assumed that the riprap stones are nearly uniform with very little gradation coefficient, i.e., the sediment mixtures which was used in these experiments were nearly uniform. Therefore, the D50 in the laboratory data can be taken to be equal to the ${\text{d}}_{\text{min}}$ appearing in Eq. (12). In other words for uniform mixtures there will be no noticeable distinction between the median diameter and the minimum diameter. Table 3 shows the percentage relative errors resulted from applying the existing formulas in Table 1 and Eq. (12) to the experimental data by Quazi et al.¹¹ and Parola¹³ which are shown in Table 2. Methods based on trial and error approaches will not be used here. The percentage relative error is defined as:

$\text{relative}\text{error}\text{=}\frac{\left({\text{d}}_{\text{predicted}}\text{-}{\text{d}}_{\text{measured}}\right)}{{\text{d}}_{\text{measured}}}\text{×}\text{100}$(15)

Where
dpredicted is the predicted riprap size while
dmeasured is the measured riprap size.

In Table 3 the present approach full equation as by Eq. (12) is considered as case (b) while case (a) assumes unity for the terms in parenthesis i.e. $\left(\text{1+H/}{\text{C}}_{\text{max}}\text{ b}\right)\text{ = 1}$in the right hand side of Eq. (12). The coefficient ${\text{C}}_{\text{max}}$ was taken as recommended by Raudkivi²³ as 2.3 in Eq. (12), case (b). Figure 1A, Figure 1B shows comparison between the experimental data and the predictions by Eq. (12) where most of the predictions are clustered above the line of best fit. From Table 3, it is clear that Breusers et al.²⁷ highly overestimate the riprap sizes while Breusers et al.²³ highly underestimate the riprap sizes in agreement with Melville et al.⁵ findings. The equations of Lauchlan,⁶ Chiew,¹⁴ Austroads,²⁸ also give high estimations which yield them as design equations. The rest of the equations give reasonable predictions with Parola¹² and the present approach, Eq. (12) giving the closest agreement to measured data followed by Richardson et al.³ The present approach case (a) which does not include the pier width effects gives more underestimates compared to case (b). Quazi et al.,¹¹ Farradayet al.²⁹ and the present approach case (a) give more underestimates compared to the rest of the equations. Froehlich¹⁵ presented graphically the results of applying his analytical equation of sizing riprap to the data of Table 2.^30,31

Figure 1 Schematic diagrams of scour at a bridge pier in the symmetry plane.
A. Longitudinal–flow–transformation into down flow
B. Particles movement out of the Scour–hole

Form his graph of the measured dimensionless riprap size to the calculated one it is clear that the line of perfect agreement nearly divides the data points indicating almost equal under and over estimation. Visually one can find at least thirty points of under predictions. He used a factor of safety of 1.25 to eliminate the under–predictions. The complexity of his approach and the amount of empiricism in it in addition to the amount of under–predications does not make it favorable. The present approach case (b) gives only 6 underestimates out of 91 predictions of riprap sizes and their relative error values are relatively small amounting to –1%, –5%, – 13%, –4%, –27%, and –16%. Keeping in mind that due to data availability the velocity used in applying Eq. (12) was the average cross–sectional velocity while the velocity just upstream the pier is the one which should be used instead. If amplification of velocity by 20% is applied these underestimates would disappear when applying Eq. (12), case (b). Nonetheless, Eq. (12) case (b) performance is very good where it shows the important effect of the pier width and water depth that is supported by the findings of Karimaee et al.⁸ and Karimaee et al.¹⁶

Waves and seismic effects

The hydrodynamic jet flow force due to stream currents hitting the bridge pier was given before as $\rho {\left(\text{VZ}\right)}_{\text{2}}{\text{A}}_{\text{p}}\left(\text{H+ }{\text{D}}_{\text{s}}\right)$which can be written as $\text{(}{\text{A}}_{\text{p}}{\text{F}}_{\text{H}}{\text{L}}_{\text{H}}\text{ )}$ where ${\text{F}}_{\text{H}}\text{ =}\rho {\left(\text{VZ}\right)}_{\text{2}}$ which is the force per unit area and LH = (H+ Ds) is the distance of the force above the deepest point of the scour hole. The wave forces acting on a bridge pier can be written in a similar fashion as Ap Fw Lw where Fw is the wave force per unit area and Lw is the distance of the force above the deepest point of the scour hole. Similarly the seismic forces can be written as

$\left({\text{A}}_{\text{p}}{\text{F}}_{\text{SH }}{\text{L}}_{\text{SH}}\text{ + }{\text{A}}_{\text{p }}{\text{F}}_{\text{SV}}{\text{L}}_{\text{SV}}\right)$

Where
is the horizontal seismic force per unit area
${\text{L}}_{\text{SH}}$ is the distance of the horizontal force above the deepest point of the scour hole
FSV is the vertical seismic force per unit area and
LSV is the distance of the vertical force above the deepest point of the scour hole

The seismic force can be taken as the resultant of the horizontal and vertical seismic forces acting on the bridge pier. The inclusion of the wave and seismic forces in addition to the hydrodynamic force in inequality (1) yields

$\lambda \text{(}{\text{A}}_{\text{p}}\text{)}\text{(}{\text{F}}_{\text{H}}\text{}{\text{L}}_{\text{H}}\text{}\text{+F}{}_{\text{W}}\text{}{\text{L}}_{\text{W}}\text{}\text{+}{\text{F}}_{\text{S}}\text{}{\text{L}}_{\text{S}}\text{)}\le \text{(}{\gamma }_{\text{s}}\text{-}\gamma \text{)}\text{(Vol)}{\text{D}}_{\text{s}}$ (16)

Where the transfer coefficient λ is used as before. Following the same treatment as was done before the following equation results in for the minimum stable riprap size as:

$\text{d}\text{=}\frac{\text{1}\text{.5}\lambda \text{(}{\text{F}}_{\text{H}}\text{}{\text{L}}_{\text{H}}\text{}\text{+F}{}_{\text{W}}\text{}{\text{L}}_{\text{W}}\text{}\text{+}{\text{F}}_{\text{SH}}\text{}{\text{L}}_{\text{SH}}\text{+}{\text{F}}_{\text{SV}}\text{}{\text{L}}_{\text{SV}}\text{)}}{\text{(}{\gamma }_{\text{s}}\text{-}\gamma \text{)}\text{b}{\text{C}}_{\text{max}}}$(17)

Equation (17) indicates that the minimum stable riprap size increases in size in direct proportion to increase in the wave and seismic forces. Expressions for the wave and seismic forces and the distances of their point of application can be found in standard text books of coastal and geotechnical engineering.

A novel method is developed herein for riprap design of scour protection at bridge piers. The method is based on the fact that the minimum stable riprap size exists when the work done due to the attacking flow jet upstream of the bridge pier is no longer capable to lift the riprap particles out of the scour hole. The developed equation expresses the minimum particle size as a function of the longitudinal velocity just upstream of the pier, the flow depth, the bed particle specific gravity, and the pier width along with some coefficients. These coefficients reflect the transformation of the longitudinal velocity into vertical velocity upstream of the pier and the fraction of the exposed area of the riprap– particles to the flow. The equation can be made to give the minimum particle size of riprap protection corresponding to a desired flow, pier width and expected/ desired pier scour depth.

The proposed equation has the advantages that it is:

1. Theoretically based which allows considering effects of wave and seismic forces on pier scour
2. Dimensionless which allows using any system of units
3. Giving the equilibrium minimum grain or riprap size for stable conditions while previous methods give the median size D50
4. Capable of determining the bed material size for scour holes under armoring conditions;
5. Illustrative of the connection between pier width and riprap size and
6. Easy to apply and use as no trial and error procedures are required

The author would like to thank all past researchers who contributed to the subject of riprap design protection of pier scour.

The authors declare that there is no conflict of interest.

1. Raudkivi AJ. Scour at bridge piers in Scouring. In: Breusers H, Raudkivi AJ, editors. International Association of Hydraulic Research, Balkema, Rotterdam, Netherlands; 1991.
2. Hafez YI. Scour due to turbulent wall jets downstream of low–/high–head hydraulic structures. Cogent Engineering Journal. 2016b;3(1).
3. Lauchlan CS, Melville BW. Riprap protection at bridge piers. J Hydraul Eng. 2001;27(5):412–418.
4. Lagasse PF, Clopper PE, Zevenbergen LW, et al. Riprap design criteria, recommended specifications, and quality control. Washington, DC: Transportation Research Board of the National Academies (NCHRP Report 568), USA; 2006.
5. Melville BW, Coleman SE. Bridge scour, Water Resources Publications, Highlands ranch, Colorado, USA; 2000. 572 p.
6. Lauchlan CS. Pier scour countermeasures. PhD. Thesis, Civ. And Resour. Engrg, University of Auckland, New Zealand; 1999.
7. Richardson EV, Davis SR. Evaluating scour at bridges. Hydraulic Engineering Circular (HEC), No. 18, FHWA–IP–90–017, Fairbank Turner Hwy. Res. Ctr., McLean, Va, USA; 1995.
8. Karimaee Taberestani M, Zarrati AR. Design of stable riprap around aligned and skewed rectangular bridge piers. J Hydraul Eng. 2013;139(8):911–916.
9. Chiew YM, Lim FH. Failure Behavior of Riprap Layer at Bridge Piers under Live–Bed Conditions. J Hydr Eng. 2000;126(1):43–55.
10. Croad RN. Protection from scour of bridge piers using riprap, Transit New Zealand Research Report No. PR3–0071, Works Consultancy Services Ltd., Central Laboratories Lower Hutt, New Zealand; 1997. 53 p.
11. Quazi ME, Peterson AW. A method for bridge pier rip–rap design. Proceedings of the First Canadian Hydraulics Conference. Edmonton, AB: University of Alberta, Canada, 1973. p. 96–106.
12. Parola AC, Jones JS. Sizing riprap to protect bridge piers from scour. Transportation Research Record. 1989;(2):276–279.
13. Parola AC. Stability of Riprap at Bridge Piers. J Hydr Eng ASCE. 1993;119(10):1080–1093.
14. Chiew YM. Mechanics of riprap failure at bridge piers. J Hydraul Eng. 1995;121(9):635–643.
15. Froehlich DC. Protecting bridge piers with loose rock riprap. Journal of Applied Water Engineering and Research. 2013;1(1):39–57.
16. Karimaee Taberestani M, Zarrati AR. Design of riprap stone around bridge piers using empirical and neural network method. Civil Engineering Infrastructure Journal. 2015;48(1):175–188.
17. Mashahir MB, Zarrati AR, Mokallaf E. Application of riprap and collar to prevent scouring around rectangular bridge piers. J Hydraul. Eng. 2010;136(3):183–187.
18. Karimaee Taberestani M, Zarrati AR, Mashahir MB, et al. Extent of riprap layer with different stone sizes around rectangular bridge piers with ot without an attached collar. Sharif University Technology. Scientia Iranica. 2015;22(3):709–716.
19. Nohani I, bejestan MS, Masjedi A, et al. Experimental study on the riprap stability in the vicinity of a bridge pier with a collar in a 180 degree river bends. Contemporary Engineering Sciences. 2012;5(8):381–390.
20. Hafez YI. A New Analytical Bridge Pier Scour Equation. 8th International Water Technology Conference, Alexandria, Egypt; 2004.
21. Hafez YI. Mathematical Modeling of Local Scour at Slender and Wide Bridge Piers. Journal of Fluids. 2016a. 19 p.
22. Roberson JA, Crowe CT. Engineering Fluid Mechanics, 10th edition, Houghton Mifflin Company, Boston, MA 02108, USA. 1985. p. 688.
23. Breusers HNC, Raudkivi AJ. Scouring. Rotterdam, AA Balkema, Netherlands; 1991. 143 p.
24. Graf WH, Istiarto I. Flow pattern in the scour hole around a cylinder. J Hydraul Res. 2002;40(1):3–20.
25. Isbash SV. Construction of dams by depositing rock in running water, transactions, Second Congress on Large Dams, Washington, DC. USA; 1936.
26. Lagasse PF, Zevenbergen LW, Schall JD, et al. Bridge Scour and Stream Instability Countermeasures. Hydraulic Engineering Circular No. 23 (HEC–23), Second Edition, Report FHWA NHI–01–003, Federal Highway Administration, USA; 2001.
27. Breusers HNC, Nicollet G, Shen HW. Local scour around cylindrical piers. J Hydraul Res. 1977;15(3):211–252.
28. Austroads. Waterway design–A guide to the hydraulic design of bridges, culverts and floodways, Austroads, Sydney, Australia; 1994. l39 p.
29. Farraday RV, Charlton FG. Hydraulic factors in bridge design. Hydraulics Research Station, Wallingford, England; 1983. 102 p.
30. Melville BW. Coleman SE. Riprap protection at bridge piers. IABSE reports. 1999; 80 p.
31. Parola AC. Boundary stress and stability of riprap at bridge piers in River, Coastal and Shoreline Protection: Erosion Control Using Riprap and Armourstone. In: Thorne CR, Steven R Abt, Stephen T Maynord, Krystian W Pilarczyk, Frans Barends BJ, editors. John Wiley & Sons Ltd; 1995.