To predict the local damage of a concrete target subjected to impact load, various empirical and theoretical equations were proposed because the local failure mechanism of concrete on collision is complicated. In the present study, using an empirical model and an energy based model, a parametric study was performed to investigate the effects of design parameters on the penetration depth. All design parameters including concrete strength, rebar ratio, concrete density, aggregate size, steel fiber volume ratio, impact velocity, projectile mass, projectile diameter, and concrete target configuration were considered. The results showed that the energy based model is useful to predict the penetration depth of the local impact-damaged concrete target under various design conditions.
Keywords: impact load, penetration, kinetic energy, resistant energy, energy-based penetration model
High-velocity impact causes local failure in reinforced concrete structures.1,2 For civilian and military structures under impact load, the impact load resistance needs to be accurately evaluated. However, due to the complicated mechanism of concrete subjected to impact load, the impact resistance of concrete members has been studied by a number of tests and empirical methods. In order to predict the penetration depth of concrete targets, Petry et al.2 proposed a method based on a simplified equation of motion for the first time, considering the projectile mass, impact velocity, sectional area of the projectile, and factor related to concrete penetrability. Army Corps of Engineers (ACE)3 evaluated the allowable concrete target thickness to restrain significant local failure, and National Defense Research Committee (NDRC)4 and Kennedy5 additionally considered the nose shape effect of the projectile in ACE model.4 The effects of maximum aggregate size, elastic modulus of the projectile, strain-rate of concrete, thickness of the concrete target, concrete density, configuration of the projectile, and hybrid-fibers on the penetration depth of the concrete target have been studied.6-15 Unlike empirical models, Hwang et al.16 developed an energy-based model for the penetration depth and residual velocity of a projectile. Comparing the kinetic energy of a projectile with the resistant energy of a concrete target directly, the penetration depth of the concrete target can be estimated. Although the energy-based model predicts well the penetration depth of the concrete target, it is difficult to understand the effect of each design parameter on the penetration depth intuitionally in initial design stage. Thus, to investigate the impact damage of the concrete target under high velocity impact, a parametric study was performed. The modified NDRC model5 and energy-based model16 were used, and the penetration depth of the local impact-damaged concrete target under various design conditions was examined. The analysis results can provide an insight to researchers and practical engineers.
Modified NDRC
The modified NDRC method5 was developed based on the test results of plain concrete. Although various design conditions cannot be considered, the modified NDRC method has been widely used for simple calculation. The penetration depth x of concrete targets is defined as follows.
for (1a)
for (1b)
(in kg, MPa, m/s, and m) (1c)
Where d is the projectile diameter; N is the nose shape factor (= 0.72 for flat nose, 0.84 for hemispherical nose, 1.0 for blunt nose, and 1.13 for sharp nose); m is the projectile mass; f’c is the concrete compressive strength; and Vi is the initial velocity.
Energy-based penetration model
In the study of Hwang et al.,16 the penetration depth x of concrete targets is estimated by comparing the kinetic energy EK of projectile with the resistant energy ER of the concrete target. The kinetic energy EK is defined as a function of the projectile mass m, initial velocity Vi, and residual velocity Vr.
(2)
Where Vr is the residual velocity of the projectile after perforation (i.e., Vr = 0 when perforation failure does not occur).
Figure 1 shows local failure mode of concrete targets. Due to deformation of the projectile and concrete target on collision, the kinetic energy Ek is absorbed by the deformed energy EDP of the projectile and deformed energy EDC of the concrete target (Figure 1). On the basis of the idealized concrete cone and failure surface in the tunneling zone, the spalling resistant energy ES, tunneling resistant energy ET, and scabbing resistant energy EC are generated to absorb the kinetic energy Ek. The resistant energy Er of the concrete target is determined from the sum of EDP, EDC, ES, ET, and EC.
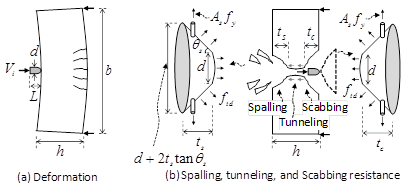
Figure 1 Local failure mode of concrete target under impact load.
(3a)
(3b)
for(3c)
for (3d)
for (3e)
Where Ap is the cross-sectional area of projectile; L is the projectile length; Ep is the elastic modulus of projectile (= 205000 MPa for steel); b is the concrete target width; Ecd is the elastic modulus of concrete targets under impact load; Ig is the gross moment of inertia of concrete target; ρp is the projectile density (= 7850 kg/m3 for steel); ks is the size effect factor (= , where h is in mm); h is the concrete target thickness; kbs and kbc is the stress concentration effect factors (= ); = 2.0, 1.9, 1.55, and 0.9 for flat, round, ogive, and sharp nose shape, respectively; ftd is the concrete tensile strength increased by strain rate effect; As is the sum of effective reinforcing bar area in the concrete cone in horizontal and vertical directions; fy is the rebar yield strength; f′cd is the concrete compressive strength increased by strain rate effect; and = 1.0, 0.9, 0.7, and 0.2 for flat, round, ogive, and sharp nose shape, respectively.
In Eqs 3c–3e, the allowable maximum spalling and scabbing depths ts and tc are affected by geometric and material properties of the concrete target, and it is defined as follows.
(4a)
(4b)
(in %) (4c)
(in kg/m3) (4d)
(4e)
where k1 is the coefficient related to the concrete target thickness; k2 is the coefficient related to the steel fiber volume ratio; k3 is the coefficient related to the concrete density ; and k4 is the coefficient related to the maximum size sa of coarse aggregates.
In Eqs. 3b–3e, impact force increases the elastic modulus Ecd, compressive strength f′cd, and tensile strength ftd of concrete due to strain rate effect, and it is defined as follows.
(5a)
(5b)
for (5c)
for (5d)
for (5e)
for (5f)
for C (5g)
for (5h)
Where is the strain rate of concrete; is the elastic modulus of concrete (=in MPa) under static load; ft is the concrete tensile strength; lf is the steel fiber length; df is the steel fiber diameter; and Vf is the volume ratio of steel fibers. The compressive and tensile strength increased by strain rate effect are specified in Model Code 2010.17 In Eq. 5e and 5f, the effect of steel fiber on the tensile strength of concrete is considered on the basis of the test results of Musmar.18
Figure 2 shows the relationship between the penetration depth x and resistant energy ER corresponding to the kinetic energy EK. When the kinetic energy EK is less than the resistant energy E1, E2, or E3, the penetration depth is linearly interpolated between 0 and x1, x1 and x2, or x2 and x3, respectively.

Figure 2 Resistant energy-penetration depth relationship.
To investigate the effects of design parameters on the penetration depth, a parametric study was performed for a concrete target under impact load. A prototype concrete target has the width b = 1000 mm; thickness h = 300 mm; concrete density = 2350 kg/m3; coarse aggregate size = 20 mm; steel fiber volume ratio = 0%; and effective reinforcing bar area As = 0 mm2. A prototype steel projectile has the diameter d = 20 mm; mass m = 100 g; initial velocity Vi = 300 m/s; length L = 40 mm; and round nose shape. Design parameters are as follows: the concrete strength ranges from 20 to 120 MPa; rebar area from 0 to 0.48 % (yield strength fy = 400 MPa); coarse aggregate size sa from 5 to 30 mm; concrete density from 2350 to 2500 kg/m3; steel fiber volume ratio Vf from 0 to 2.0% (fiber shape ratio lf / df = 60); projectile initial velocity Vi from 100 to 1100 m/s; projectile mass m from 100 to 1100 g; projectile diameter d from 10 to 60 mm; and concrete target type (single target and dual target).
Figure 3 compares the penetration predictions of the modified NDRC model5 and energy based model16 according to the concrete target parameters. As concrete strength increases, the penetration depth decreases (Figure 3). In general, the prediction of the modified NDRC model5 is greater than that of the energy based model.16 The penetration depth of the energy based model16 is significantly increased at the concrete targets using low strength concrete under impact of Vi = 600 m/s. This is because the tunneling resistance is additionally generated to absorb the kinetic energy in the concrete target using low strength concrete. Reinforcing bars improve the spalling and scabbing resistance, which decreases the penetration depth and damage (Figure 3B). The use of small aggregate size and concrete with large density increase the penetration depth because the impact force of the projectile easily passes through small coarse aggregate in the concrete target (Figure 3C). The use of steel fibers increases the flexural tensile strength of concrete, which decreases the penetration depth (Figure 3D).
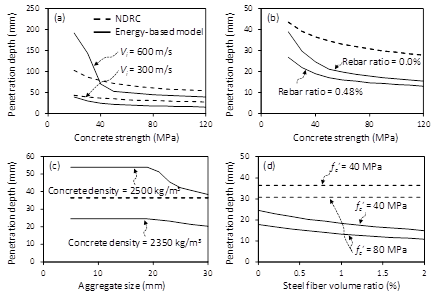
Figure 3 Penetration depth according to design parameters of concrete target.
Figure 4 compares the penetration predictions of the modified NDRC model5 and energy based model16 according to the projectile parameters. As the impact velocity increases, the penetration depth increases. Particularly, the prediction of the energy based model16 is significantly increased at Vi = 600 ~ 700 m/s because the tunneling resistance is activated (Figure 4A). Projectile mass increases the kinetic energy, which increases the penetration depth, but the increase ratio is reduced at a certain level (Figure 4B). Thus, although both the impact velocity and projectile mass increases the impact energy, the impact damage of the concrete target is more vulnerable to the high-velocity impact than the heavy-mass impact. Large projectile diameter increases the resisting area of the concrete target, which decreases the penetration depth.
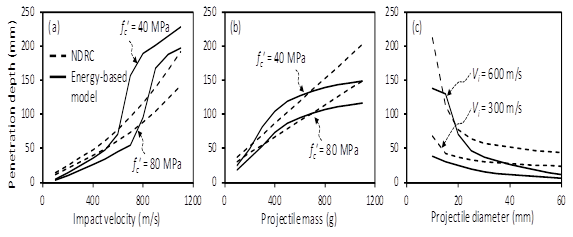
Figure 4 Penetration depth according to design parameters of projectile.
Figure 5 compares the effect of the number of concrete target on the penetration depth. Single concrete target has a thickness of 300 mm, and dual concrete target consists of two concrete targets with a thickness of 150 mm. Under low-velocity impact, the single concrete target exhibits better penetration resistance than that of the dual concrete target. However, the penetration depth of the single concrete target is significantly increased at Vi = 600~700 m/s due to tunneling failure. In the dual concrete target, perforation failure occurs in the first target at Vi = 700 m/s. As a result, larger impact energy can be dissipated by additional scabbing resistance of the first concrete target at the same penetration depth. Ultimately, the penetration depth can be reduced in the dual concrete target under large impact load. Reinforcing bars in the dual concrete target decreases the penetration depth effectively.
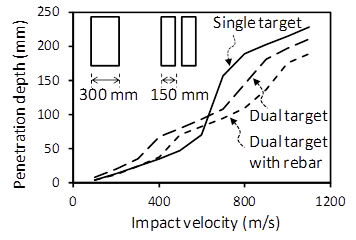
Figure 5 Penetration depths according to the number of concrete target.
Figure 6 shows the minimum thickness of concrete target to avoid perforation failure (i.e., EK = ER) according to concrete strength. Although the same kinetic energy EK is considered, the penetration depth is more vulnerable to high-velocity impact. As concrete strength increases, the concrete target thickness decreases. In general, the concrete target thickness is decreased by about 30% at every two times concrete strength. When reinforcing bars are used, the concrete target thickness is decreased by only 5%. The use of steel fiber with 2.0% volume ratio decreases about 18% of the concrete target thickness. Thus, high strength fiber-reinforced concrete is recommended to improve the impact resistance of concrete targets.
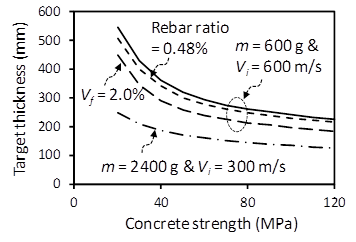
Figure 6 Minimum thickness of concrete target without perforation failure.


