Objectives: Total bilirubin and direct bilirubin are known as liver disease biomarkers. The report aims to identify the explanatory factors of total bilirubin of some liver patients based on appropriate probabilistic modeling.

Background: Liver disease biomarkers are interrelated, and the associations of total bilirubin with the other liver disease markers are little known in the literature.

Materials and Methods: A real data set of 579 liver & non-liver disease patients, along with 2 attribute characters and 9 continuous variables is considered, which was obtained from the North-East of Andhra Pradesh, India. The interested response total bilirubin is continuous, heterogeneous, positive, and non-normally distributed which is generally analyzed by joint generalized linear statistical Log-normal or Gamma models.

Results: Total bilirubin (TB) is higher for male liver patients (P=0.0543) than female. Mean TB is higher at older ages (P=0.0400). It increases as alkaline phosphatase (ALP) (P<0.0001), or direct bilirubin (DB) (P<0.0001), or alanine aminotransferase (SGPT) (P=0.1233), or albumin (ALB) (P=0.0101) increases. Mean TB decreases as the total proteins (TP) (P=0.0942), or albumin to globulin ratio (A/G) (P=0.0239), or joint interaction effect of ALP & DB (ALP*DB) (P<0.0001), or interaction effect of aspartate aminotransferase (SGOT) & SGPT (SGOT*SGPT) (P=0.0856), or interaction effect of DB & TP (DB*TP) (0.0389) increases. Variance of TB is higher for male liver patients (P=0.0051) than female, and it increases as DB (P<0.0001), or ALP (P=0.0327) increases.

Conclusions: Total bilirubin has a complex association with all liver disease markers. Age, ALP, DB, SGPT, ALB are directly correlated with the mean TB, while sex, A/G, ALP*DB, SGPT*SGOT, DB*TP are inversely correlated with the mean TB. These findings are completely new in the liver disease literature.

Keywords: alanine aminotransferase; direct bilirubin; joint log normal model; liver disease markers; total bilirubin

VTB, variance of TB; DB, direct bilirubin; TP, total proteins; JGLMs, joint generalized linear models; AIC, akaike information criterion; ALP, alkaline phosphatase; MTB, mean total bilirubin

Liver is a vital organ of human being which performs many important functions such as glycogen storage, protein synthesis, detoxification, decomposition of red blood cells, and production of biochemical & hormone. It has multidimensional functions, and it is also prone to many diseases. There are many risk factors which are responsible for developing more than 100types of liver disease.^1‒4 Over the world, liver disease is the most common disease which is developed due to inflammation hepatocyte in liver.^5‒8 The incidence of new liver cancer disease patients in every year throughout the world is more than one million.^9,10 Liver disease is very hard to detect, as liver is capable to maintain its normal activity even it is partially damaged. The early stage diagnosis of hepatic fibrosis, hepatitis, and hepatic cirrhosis is very complicated as their morphological changes are not always visible. However, some hemodynamic liver disease changes are observed in practice.^10‒12 Therefore, the early diagnosis of the liver disease is the fundamental steps for its treatment.

Our body sometimes breaks down old red blood cells; consequently a substance is produced known as bilirubin. It is a product of heme catabolism that may have potent cytoprotective and antioxidant properties.^13,14 A little amount of bilirubin in our blood is normal (0.22–1mg/dl), but a higher amount may be a sign of liver disease. Earlier research articles have pointed that higher levels of bilirubin for a healthy body are negatively associated with the prevalence of diabetes, insulin levels, and cardiovascular disease.^15,16 Dietary factors such as fat, alcohol have significant effects on liver disease markers.^17‒19 In animals or healthy humans, fat ingestion has been identified to elevate serum ALP levels. It is happened either if a high-fat diet is absorbed or if fat is included in a test meal.^20‒22 Intravenous infusion of glucose in rabbits develops an increase in the hepatic excretion of conjugated bilirubin.²³ Some medium-chain fatty acids reduce in binding of bilirubin to albumin in vitro.²⁴ More alcohol consumed (>80g/day for more than 5years) (without other causes of cirrhosis) may develop alcoholic cirrhosis.^25,26

The role of explanatory factors of total bilirubin for the liver patients is little known in the literature, considering the practical situations that the total bilirubin is positive, heteroscedastic and non-normal continuous random variable. Based on the appropriate characteristics of total bilirubin, it may be properly analyzed by joint generalized linear models (JGLMs), specifically; joint Log-normal or gamma models.^27‒30 These two analysis methods are applied to analyze the present considered data set, and it is found that the joint Log-normal models fit gives better results than joint gamma models, so only the results of joint Log-normal models fit are displayed in Table 1. The following hypotheses are aimed to examine in the report. What are the determinants of total bilirubin? What is the role of the explanatory factors on TB? How are the determinants associated with TB? With the help of a real data set containing 579 liver & non-liver patients with 2 categorical characters and 9 continuous variables, the above hypotheses are examined in the report.

Materials
The report considers a real data set containing 579 liver & non-liver patients which has been collected from the North-East of Andhra Pradesh, India. The data is given in the site http://archive.ics.uci.edu/ml/machine-learning-databases/00225/". It contains 9 continuous variables and 2 categorical characters which are age, alkaline phosphatase (ALP), direct bilirubin (DB), total bilirubin (TB), aspartate aminotransferase (SGOT), alanine aminotransferase (SGPT), albumin (ALB), total proteins (TP), and albumin and globulin ratio (A/G), sex (male = 0, female =1), subject type (liver patient=0, non-liver patient=1) (CLUSTER). In the given data set, there are 28.5% non-liver and 71.5% liver patients, and also 24.18% female and 75.83% male subjects. The summarized statistics of the variables are given in Hastie T et al.,31 (Table 1).

Statistical methods

For some continuous positive response variable, variance is not constant always in its range of variation. In practice, physiological data such as total bilirubin, direct bilirubin, alkaline phosphatase are non-constant variance response. They are generally analyzed by joint generalized linear Log-normal or gamma models, and their detailed discussions are given in.27‒30 The response total bilirubin is analyzed by both the joint Log-normal and gamma models, and it is found that joint fitted Log-normal models give better results than joint gamma fitted models. Therefore, only the joint Log-normal models are shortly described herein.

For the positive response random variable Yi ’s, with

$E\left(Y_i\right)={\mu }_i$ and $Var\left(Y_i\right)={\sigma }_i{}^2{\mu }_i{}^2$

The log transformation Zi=log(Yi) is applied to stabilize the variance Var (Zi)≈ . In order to obtain better models, an improved statistical technique is applied. In practice, a simple log transformation does not stabilize the variance always.28 Then Nelder and Lee32 have proposed to apply joint generalized linear models (JGLMs).

For the positive dependent continuous variable Yi, generally the log transformation Zi=logYi is applied. The JGLMs (under Log-normal distribution) for the mean and variance are given by

$E\left(Z_i\right)={\mu }_{zi} and Var\left(Z_i\right)={\sigma }_{zi}^2$

${\mu }_{zi}=x_i{}^t\beta and log\left({\sigma }_{zi}{}^2\right) = g_i{}^t\gamma$

Where x_i^t and g_i^t denote respectively, the row vectors for the regression coefficients β (mean model) and γ (variance model). Note that the mean parameters β’s are estimated by maximum likelihood method (MLE), and the variance parameters γ’s are estimated by restricted likelihood method (REML).

In GLMs, the variance consists of two parts which are $V({\mu }_i)$ depending on mean) and ${\sigma }_i{}^2$ (independent of mean). Note that $V({\mu }_i)$ (known as variance function) identifies the GLMs family distributions. For example, the distribution is gamma if $V\left(\mu \right)={\mu }^2$ Poisson if $V\left(\mu \right)=\mu$ and Normal if $V\left(\mu \right)=1$ etc.

In the present article, it is aimed to examine the determinants of total bilirubin which is a liver disease marker. Higher level of TB may suggest some liver problems such as gall bladder, cirrhosis (scarring), hepatitis (infection), gallstones, liver cancer etc. The report tries to identify the determinants of TB using the above stated joint Log-normal models as they give better results than the joint gamma models. Using the joint Log-normal models, the estimated models of total bilirubin have been derived in the report which is displayed in Table 1. Based on the derived models in Table 1, the determinants, and their effects on TB have been identified in the report.

Total bilirubin is a positive, continuous and heteroscedastic response variable, which is to be modeled using the remaining 2 attribute and 8 continuous variables. TB is modeled using the joint Log-normal models as stated above. On the basis of lowest Akaike information criterion (AIC) value, the final joint Log-normal fitted models (with AIC=699.3) have been selected which are displayed in Table 1. Note that AIC identifies a model that minimizes squared error loss and predicted additive errors.³³ Based on marginality rule (if an interaction term is significant in the model all its related lower-order interactions and main effects should be included in the model³⁴) two insignificant effects are included in the mean model (Table 1). One insignificant effect is included in the dispersion model (Table 1) for better fitting.²⁹ Absolute residuals and normal probability plots are used as the model checking diagnosis plots.

For the fitted Log-normal models (Table 1), absolute residuals are plotted with respect to fitted values in Figure 1(a), which is almost flat except the right tail. The right tail of Figure 1(a) is decreasing as the smallest absolute residual is located at the right boundary. Figure 1(a) is almost flat indicating that the variance is constant with the running means. Figure 1(b) reveals the normal probability plot of the fitted mean model in Table 1, which does not show any lack of fit due to outliers, or model selection, or distribution (Figure 1).

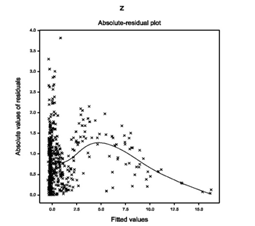
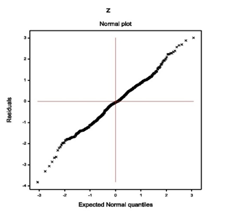
Figure 1(a)                                                                                     Figure 1(b)

Figure 1 For the fitted Log-normal models of TB (Table 1), the (1A) absolute residuals plot with respect to fitted values, and the (2B) normal probability plot of the mean model.

Analysis results of total bilirubin

The mean total bilirubin (TB) is directly correlated with the age (P=0.0400), or alkaline phosphatase (ALP) (P<0.0001), or direct bilirubin (DB) (P<0.0001), or alanine aminotransferase (SGPT) (P=0.1233), or albumin (ALB) (P=0.0101). Also mean TB is inversely correlated with the sex (P=0.0543), or joint interaction effect of ALP & DB (ALP*DB) (P<0.0001), or interaction effect of aspartate aminotransferase (SGOT) & SGPT (SGOT*SGPT) (P=0.0856), or total proteins (TP) (P=0.0942), or interaction effect of DB & TP (DB*TP) (0.0389), or albumin to globulin ratio (A/G) (P=0.0239). The variance of TB is directly correlated with DB (P<0.0001), or ALP (P=0.0327), and it is inversely correlated with the sex (P=0.0051).

Interpretations of total bilirubin analysis:

Table 1 presents the summarized results of TB analysis. The following interpretations are obtained from Table 1. The mean total bilirubin (MTB) is inversely significantly correlated with the sex (male=0, female=1) (P=0.0543), indicating that MTB is higher for male liver patients than female. MTB is directly significantly correlated with the age (P=0.0400), indicating that MTB is higher for older liver patients than younger. MTB is directly significantly correlated with alkaline phosphatase (ALP) (P<0.0001), or direct bilirubin (DB) (P<0.0001), or albumin (ALB) (P=0.0101), indicating that MTB increases as ALP, or DB, or ALB increases. MTB is inversely significantly correlated with the interaction effects of ALP & DB (ALP*DB) (P<0.0001), indicating that MTB increases as ALP*DB decreases. Note that the marginal effects ALP & DB are directly correlated with MTB, while their interaction effect ALP*DB is inversely correlated with MTB. MTB is directly partially significantly correlated with alanine aminotransferase (SGPT) (P=0.1233), indicating that MTB increases as SGPT increases. Note that SGPT is partially significant with MTB, which is known as confounder in epidemiology. In addition, MTB is directly insignificantly correlated with aspartate aminotransferase (SGOT) (P=0.4351), indicating that MTB increases as SGOT increases. It is included in the model due to marginality rule.34MTB is inversely significantly correlated with the interaction effects of SGPT & SGOT (SGPT*SGOT) (P=0.0856), indicating that MTB increases as SGPT*SGOT decreases. Here also the marginal effects SGPT & SGOT are directly correlated with MTB, while their interaction effect SGPT*SGOT is inversely correlated with MTB. MTB is inversely significantly correlated with the total proteins (TP) (P=0.0942), or albumin to globulin ratio (A/G) (P=0.0239), indicating that MTB increases as TP, or A/G decreases. MTB is inversely significantly correlated with the interaction effects of DB & TP (DB*TP) (P=0.0389), indicating that MTB increases as DB*TP decreases. Note that the marginal effect DB is directly, while TP is inversely correlated with MTB.

The variance of TB (VTB) is inversely significantly correlated with the sex (male=0, female=1) (P=0.0051), indicating that VTB is higher for male liver patients than female. VTB is directly significantly correlated with the DB (P<0.0001), or ALP (P=0.0327), indicating that VTB increases as DB, or ALP increases. VTB is inversely partially significantly correlated with the subject type (liver patient=0, non-liver patient=1) (CLUSTER)(P=0.1743), indicating that VTB is higher for liver patients than non-liver patients. Note that CLUSTER is a confounder in the dispersion model according to epidemiology. The derived fitted Log-normal mean and variance models ( Table 1) of total bilirubin of the liver patients, respectively, are

The explanatory factors of total bilirubin of liver patients have been derived (Table 1). The derived results and their interpretations are given above. Many factors such as sex, age, ALP, DB, (ALP*DB), SGPT, SGOT, (SGPT*SGOT), TP, (DB*TP), ALB, A/G are the explanatory factors of mean total bilirubin, while sex, patients type, DB and ALP are the explanatory factors of variance of total bilirubin. Note that the liver disease markers such as ALP, DB, SGPT, SGOT, ALB are positively associated with TB. In addition, some of their interaction effects such as (ALP*DB), (SGPT*SGOT), (DB*TP) are negatively associated with the mean total bilirubin. It is observed herein that liver disease markers are positively associated with the mean total bilirubin, while their interaction effects are negatively associated with the mean total bilirubin. As a result, the functional relationship of TB with other liver disease markers is very complicated. Consequently, it is very difficult to identify a patient with liver disease.

Earlier reports have shown that TB is associated with diabetes mellitus,³³ cardiovascular disease,³⁴ serum iron,³⁵ and there is no significant association in connection to other parameters in groups of male and female.³⁵ The present report has identified many determinants of total bilirubin. It ( Table 1) has shown that mean and variance of TB are higher for male liver patients than female. Mean TB increases at older ages. Mean TB has positive significant association with direct bilirubin, alkaline phosphatase, aspartate aminotransferase, albumin. It has three negative significant two factor interaction effects. In addition, variance of TB has three significant determinants.

The fitted mean and variance models of TB are given above. Note that the estimate of regression coefficients have very small standard errors ( Table 1) indicating that estimates are stable. Final models have been selected on comparison of Log-normal and gamma fitted models. Model fitting diagnostic plots do not show any lack of fit. Therefore, research should have more faith in the present results ( Table 1) than any other results using the Log-Gaussian and gamma constant variance models. Many determinants of total bilirubin have been identified in the fitted models. These results can help the medical practitioners to take necessary action to control the bilirubin level. Care should be taken on bilirubin level at older ages.

The author is very much indebted to referees who have provided valuable comments to improve this paper.

The author confirms that this article content has no conflict of interest.

1. Rang HP, Dale MM, Ritter JM, et al. Pharmacology. 5th ed. Bath: Churchill Livingstone; 2003;4(2):151.
2. Robbins SL, Kumar V, Cotran RS. Robbins and Cotran Pathologic Basis of Disease. Philadelphia, PA: Saunders/Elsevier; 2010.
3. El-serag HB, Mason AC. Rising incidence of hepatocellular carcinoma in the United States. N Engl J Med. 1999;340(10):745–750.
4. Tanaka M, Fukui M, Tomiyasu K, et al. Low serum bilirubin concentration is associated with coronary artery calcification (CAC). Atherosclerosis. 2009;206(1):287–291.
5. Deuffic S, Poynard T, Buffat L, et al. Trends in primary liver cancer. Lancet. 1998;351(9097):214–215.
6. Godley PA, Sandler RS. Liver cancer, in: Digestive Diseases in the United States: Epidemiology and Impact. In: Everhart JE. NIH Publication: Washington DC.1994;227–241.
7. Kew MC. Hepatic tumors and cysts, in: Sleisenger & Fordtran’s Gastrointestinal and Liver Disease: Pathology, diagnosis, management. 6th ed. Feldman M, Sleisenger MH, Scharschmidt BF, et al. editors. Philadelphia: WB Saunders;1998:1363–1387.
8. Okuda K, Fujimoto I, Hanai A, et al. Changing incidence of hepatocellular carcinoma in Japan. Cancer Res. 1987;47(18):4967–4972.
9. Deems RO, Friedman LS, Friedman MI, et al. Relationship between liver biochemical tests and dietary intake in patients with liver disease. J Clin Gastroententerol. 1994;18:304–308.
10. El-serag HB, Mason AC. Rising incidence of hepatocellular carcinoma in the United States. N Engl J Med. 1999;340(10):745–750.
11. Lin RH. An intelligent model for liver disease diagnosis. Artif Intell Med. 2009;47(1):53–62.
12. Orrego H, Blendis LM, Crossley IR, et al. Correlation of intrahepatic pressure with collagen in the Dissespace and hepatomegaly in humans and in the rat. Gastroenterology. 1981;80(3):546–556.
13. Stocker R, Yamamoto Y, McDonagh AF, et al. Bilirubin is an antioxidant of possible physiological importance. Science. 1987;235(4792):1043–1046.
14. Baranano DE, Rao M, Ferris CD, et al. Biliverdin reductase: a major physiologic cytoprotectant. Proc Natl Acad Sci USA. 2002;99(25):16093–16098.
15. Lin LY, Kuo HK, Hwang JJ, et al. Serum bilirubin is inversely associated with insulin resistance and metabolic syndrome among children and adolescents. Atherosclerosis. 2009;203(2):563–568.
16. Tanaka M, Fukui M, Tomiyasu K, et al. Low serum bilirubin concentration is associated with coronary artery calcification (CAC). Atherosclerosis. 2009;206(1):287–291.
17. Deems RO, Friedman LS, Friedman MI, et al. Relationship between liver biochemical tests and dietary intake in patients with liver disease. J Clin Gastroententerol. 1994;18(4):304–308.
18. Larkin FA, Metzner HL, Thompson FE, et al. Comparison of estimated nutrient intakes by food frequency and dietary records in adults. J Am Diet Assoc. 1989;89(2):215–223.
19. McDowell CM, Ross MH. Dietary fat, age and hepatic alkaline phosphatase activity in the rat. Growth.1966;30:177–185.
20. Malagelada JR, Stolbach LL, Linscheer WG. Influence of carbon chain length of dietary fat on intestinal alkaline phosphatase in chylous ascites. Am J Dig Dis. 1977;22(7):629–632.
21. Young GP, Friedman S, Yedlin ST, et al. Effect of fat feeding on intestinal alkaline phosphatase activity in tissue and serum. Am J Physiol. 1981;241(6):461–468.
22. Muñoz ME, González J, Esteller A. Effects of glucose administration on bilirubin excretion in the rabbit. Experientia. 1987;43(2):166–168.
23. Brodersen R. Free bilirubin in blood plasma of the newborn: Effects of albumin, fatty acids, pH, displacing drugs, and phototherapy, in: Intensive Care in the Newborn. In: Stern L, Oh W, Friis-Hansen B, editors. New York: Masson Publishing;1978;331–345.
24. Das RN. Relationships of liver biochemical parameters and effects of wine drinking. Model Assisted Statistics and Applications. 2013;8(2):163–175.
25. Lee Y, Nelder JA, Pawitan Y. Generalized Linear Models with Random Effects (Unified Analysis via H-likelihood). 1st ed. New York: Chapman & Hall;2006. p. 416.
26. Das RN, Lee Y. Log normal versus gamma models for analyzing data from quality-improvement experiments. Quality Engineering. 2008;21(1):79‒87.
27. Das RN, Park JS. Discrepancy in regression estimates between log-normal and gamma: Some case studies. J Applied Statistics. 2012;39(1):97‒111.
28. Firth D. Multiplicative errors: log-normal or gamma? Journal of the Royal Statistical Society. Series B (Methodological). 1988;50:266‒268.
29. Das RN, Mukherjee S, Sharma I. Alkaline Phosphatase Determinants of Liver Patients. JOP J of Pancreatic. 2018;19(1):1‒6.
30. Nelder JA, Lee Y. Generalized linear models for the analysis of Taguchi-type experiments. Applied Stochastic Models and Data Analysis. 1991;7(1):107‒120.
31. Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning. New York: Springer-Verlag;2001. P. 745.
32. Nelder JA. The statistics of linear models: back to basics. Statistics and Computing. 1994;4(4):221–234.
33. Cheriyath P, Gorrepati VS, Peters I, et al. High Total Bilirubin as a Protective Factor for Diabetes Mellitus: An Analysis of NHANES Data From 1999–2006. J Clin Med Res. 2010;2(5):201‒206.
34. Suh S, Cho YR, Park MK, et al. Relationship between serum bilirubin levels and cardiovascular disease. PLoS ONE. 2018; 13(2): e0193041.
35. Witek K, Ścisłowska J, Turowski D, et al. Total bilirubin in athletes, determination of reference range. Biol Sport. 2017;34(1):45–48.