With the help of the physical laws of flow, it is possible to describe the entire human blood circulation. However, this requires precise knowledge of the individual parameters. Within this, the determination of the flow rate included in the law of continuity is essential. Together with the data of the heart and circulation examination procedures, in order to establish the average human blood circulation, an intermediate velocity value must be selected, which is located in the middle between the two extreme velocities of the blood circulation. Another important factor from the point of view of the structure and operation of the model is the value of the earth's surface gravity. By finding the average flow speed value and using ‘g’, a torus-shaped circulation can be created, which can actually reflect the circulation conditions. By further refining the model, the pulmonary and systemic circulations can be separated and a ‘folded figure eight’ model can be formed. This realistically reflects the different sizes, flow and pressure conditions of the two blood circulations, as well as the work of the left and right sides of the heart.

Keywords: earth’s surface gravity, weight of bodies, fluid flow laws, pulmonary and systemic circulation, blood circulation velocity, cardiac output, die dilution method, single blood circulation time, cardiac ultrasound measurements

To model human blood circulation, it is necessary to define and use many physiological parameters. While some of these data are well-known and well-defined datasets, some values that have not been determined so far are essential for the model describing the blood circulation as a whole. This objective can be achieved by having the data necessary to use the fluid flow laws.¹ Until now, medicine, more specifically cardiology, has mainly dealt with the law of intensity, or in other words calculated with minute volume.² The applicability of the law of continuity of liquids when determining the parameters of the circulation runs into limitations, since two components of the relationship are unknown. Even if the intensity is known from the quotient of blood volume and blood flow time, the value of the flow cross-section area and flow velocity may vary within the product. However, if we arbitrarily choose an average blood flow rate in the circulation that corresponds in size and quality to clinical experience, then the model can be set up. Having the value of the intensity and knowing the chosen average flow velocity, the area of the flow cross-section can be determined. The definition of pressure, work and power in a circulation model to be established in relation to the driving force is not sufficiently clarified. In the human body, the driving force established by the heart as a causal factor is trivial. However, this can be paralleled by the idea that the driving force in a model is also influenced by the weight of the blood in the vascular system. In this way, the maintaining force of the circulation can be determined in the model by calculating the value of g on the earth's surface. This can only be defined in a special case, i.e., as a compressive force acting on the base of a blood column. This static idea could be represented by obeying the compressive force from the weight of the blood column by momentarily opening the plate that closes the bottom of the tube and letting out a small fragment of it³ by repeatedly returning this fraction to the top of the blood column, working against gravity, and the method can be made dynamic. This creates a kind of hydrodynamic circulation that can even be sustained permanently (n_1,2,3…). This is similar to that experienced in human blood circulation and figuratively corresponds to the fractional functioning of the human heart. It can also be compared with the work done during each of its contractions.⁴

The relationship between the mass of physical bodies and biological individuals on the Earth's surface

The weight (W) of the bodies on the surface of the earth, but also of the biological creatures, is equal to the force (F) with which they press the surface due to the gravity of the Earth. Weight is the product of the mass of bodies (m) and the gravity of the Earth's surface (g). According to Newton's law of gravitation, the force of attraction (F) between the body and the Earth is directly proportional to their masses (m, M) and inversely proportional to the square of their distance (r²) which is equal with the Earth’ radius (the mass of the Earth at its center).⁵ Since W = F, not only the body on the surface of the Earth but also the mass of the individual at a given level of development in Darwinian evolution is lost (only the mass of the Earth remains in the Formula 1).

$\begin{array}{l}{W}_{weight}=F_{force},s{o}_{},{{\displaystyle }}_{}{m}_{bod{y}_{}o{r}_{}livin{g}_{}organism}\cdot g_{Earth\text{'}surface}=G\cdot \frac{m_{bod{y}_{}o{r}_{}livin{g}_{}organism}\cdot M_{Earth}}{r_{Earth}{}^2},\\ and:\\ g_{Earth\text{'}surface}=\frac{G\cdot M_{Earth}}{r_{Earth}{}^2}\end{array}$   (1)

Where G is the gravitational constant (6.673848·10^-11m³·kg^-1·s^-2).
Figure 1 A simplified representation to explain the relationship between human blood circulation and Earth's gravity (g). From this point of view, objects on the earth's surface and biological beings behave similarly. Both exert a force (F) on the earth's surface in proportion to their mass (m). This compressive force is determined by the product of the given mass of blood and the value of gravity on the earth's surface (F=m∙g). This force effect provides an opportunity to determine other parameters of the circulation (e.g., W_work). If the circumference of the blood circulation, or the height of its straightened version (s) increases, its weight/mass (W_weight; m) also increases in parallel. The consequence of which is an increase in the compressive force (F) acting on the base (A). This upright static model could be represented by using the compressive force resulting from the weight of the blood column, momentarily opening the plate delimiting the bottom of the tube and releasing a small part of it. If this fraction is returned to the top of the blood column by working against gravity (W_work=m∙g∙s), and then repeating this operation several times, the method can be made dynamic.

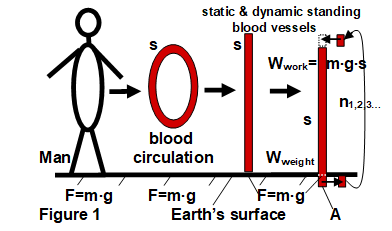
Figure 1 A simplified representation to explain the relationship between human blood circulation and Earth's gravity (g).

Average human blood circulation in relation to the laws of fluid flow

There are two fundamental laws regarding the flow of fluids. One expresses the flow intensity (Eq.2, left side) the other is the law of continuity (Eq.2, right side).⁶ Using them (separately but also together), the intensity (I), length (s), radius (r) and cross-sectional area (A) of the circulating fluid as well as the flow velocity (v) can be determined with the knowledge of the appropriate members. Since:

$I=\frac{V_{2\pi }}{t_{2\pi }}=\frac{A\cdot s_{2\pi }}{t_{2\pi }}{{\displaystyle }}_{}and{{\displaystyle }}_{}I=A\cdot v$   (2)

However, Eq. 2 on the left has two unknowns, i.e. A and s are unknown. Thus, even if V and t are known, the cross sectional area and path cannot be calculated. Eq. 2 on the right also has two unknowns, since even if the intensity can be calculated based on the formula on the left of Eq.2, A and v cannot be determined separately. However, combining the two equations does not give us the opportunity to calculate A and s either. In fact, only intensity can be accurately determined. According to them, the following limited possibilities exist.

Equating the two formulas (left and right of Eq. 2) based on intensity (I) and flow cross-sectional area (A):

$\begin{array}{l}\frac{A\cdot s_{2\pi }}{t_{2\pi }}=A\cdot v{}_{},{{\displaystyle }}_{}so,{{\displaystyle }}_{}\frac{s_{2\pi }}{t_{2\pi }}=v_{},{{\displaystyle }}_{}and{{\displaystyle }}_{}{s}_{2\pi }=v\cdot t_{2\pi },\\ and:\\ A=\frac{I\cdot t_{2\pi }}{s_{2\pi }}{{\displaystyle }}_{}and{{\displaystyle }}_{}A=\frac{I}{v},{{\displaystyle }}_{}so{{\displaystyle }}_{}\frac{I\cdot t_{2\pi }}{s_{2\pi }}=\frac{I}{v}{{\displaystyle }}_{}and{{\displaystyle }}_{}\frac{t_{2\pi }}{s_{2\pi }}=\frac{1}{v}{{\displaystyle }}_{}and{{\displaystyle }}_{}v\cdot t_{2\pi }=s_{2\pi }\end{array}$   (3)

After simplifying with A and then with I, a path-time-velocity relation valid for the flow laws is obtained. In this way, however, the flow cross-sectional area (A) is lost as a key factor, which is indispensable for a model that includes all flow-related physical factors.

By equating the two laws, the combination of the four factors (A, v, s, t) in full compatibility with the others, eliminating uncertainties, can correctly reflect the conditions actually occurring in the human body in the form of a so-called ‘average human blood circulation model’.

The relationship between blood circulation time, heart stroke volume, heart rate and flow intensity

To create an average human blood circulation model, it is first necessary to determine the single circulation time (t_{turnaround time} or t_2π) in the human body. This can be measured with various circulation testing procedures. This can be done using the dye dilution,⁷ heat dilution,⁸ or radiocirculation,^9,10 method, which takes 25-30 seconds in a healthy adult at rest. The volume of blood (V_{turnaround volume}) for this time interval must then be calculated. The most important factor in this regard is how much blood the heart pushes to the periphery during a contraction, or systole. In a person of average body weight, when the left ventricle of the heart is completely filled with blood, its so-called end-diastolic volume (EDV) is equal to 120 ml. However, when the left ventricle of the heart is in a state after full contraction, the end-systolic volume (ESV) is 50 ml. The difference between the two volumes equals the so-called stroke volume (sv), which is 70 ml.¹¹ As another key factor, it is necessary to determine, the time interval during which a single contraction of the heart takes place. In medical physiology, the number of heart contractions is usually related to the duration of one minute. Knowing the number of blood volumes resulting from a single heart contraction and the time interval required for this, the multiple of the basic unit, the fractional number can be determined.¹² Dimensional relationship between heartbeats (n) and time interval (t; e.g., 1 minute):

$\frac{n}{t_{\min ute}}{{\displaystyle }}_{};{{\displaystyle }}_{}\frac{n}{\min }=n\frac{1}{\min }{{\displaystyle }}_{};{{\displaystyle }}_{}60\frac{1}{\min }=\frac{60}{\min }=\frac{60}{60s}=1\frac{1}{s}$   (4)

n: heart beat number, t: a certain time interval

According to them, the following ratio pair can be established: 1 heart contraction or 1 pulse beat is proportional to 1 second, as the unknown number of pulses (n) is proportional to the known time interval (for example, 30-60 seconds):

$\frac{1_{contraction}}{n}=\frac{1s}{30s},{{\displaystyle }}_{}n={30}_{contraction}{}_{},{{\displaystyle }}_{}and:{{\displaystyle }}_{}\frac{1_{contraction}}{n}=\frac{1s}{60s},{{\displaystyle }}_{}n={60}_{contraction}$   (5)

The dimensionless number is obtained by dividing the time intervals that take place in the circulation, specifically the time of one turn of the circulation (t_2π) and the time of one contraction of the heart (t_1contraction). Since the time dimensions cancel each other, we get the number of heart contractions (n).

$\frac{t_{2\pi (25)}}{t_{1contraction}}=n_{25}={25}_{}{,}_{}an{d}_{}\frac{t_{2\pi (30)}}{t_{1contraction}}=n_{30}={30}_{}{,}_{}an{d}_{}\frac{t_{2\pi (60)}}{t_{1contraction}}=n_{60}=60$   (6)

The same applies to the proportion of blood volume (V). A larger volume means a longer single circulation time. In contrast, a single contraction of the heart lasts a short time. The ratio of the two will be the same dimensionless number, which the number of heart contractions (n).

$\frac{V_{turnaround(25)}}{sv}=n_{25}={25}_{}{,}_{}an{d}_{}\frac{V_{turnaround(30)}}{sv}=n_{30}={30}_{}{,}_{}an{d}_{}\frac{V_{turnaround(60)}}{sv}=n_{60}=60$   (7)

 The relative ratio of the time intervals:

$\frac{t_{2\pi (25)}}{t_{2\pi (60)}}=\frac{25s}{60s}=\frac{25}{60}={0.4166}_{}{,}_{}or:{{\displaystyle }}_{}\frac{t_{2\pi (60)}}{t_{2\pi (25)}}=\frac{60s}{25s}=\frac{60}{25}=2.4$   (8)

The ratio of the time of one revolution of blood circulation (t_2π) and the time of systole (t_1contraction), as well as their variants, are as follows. The ratio of these time variants also shows the interchangeability index (n_x/n_y) between them:

$\frac{\frac{t_{2\pi (25)}}{t_{1contraction}}}{\frac{t_{2\pi (60)}}{t_{1contraction}}}=\frac{n_{25}}{n_{60}}=\frac{25}{60}={0.416}_{}{;}_{}\frac{\frac{t_{2\pi (30)}}{t_{1contraction}}}{\frac{t_{2\pi (60)}}{t_{1contraction}}}=\frac{n_{30}}{n_{60}}=\frac{30}{60}={0.5}_{}{;}_{}\frac{\frac{t_{2\pi (60)}}{t_{1contraction}}}{\frac{t_{2\pi (60)}}{t_{1contraction}}}=\frac{n_{60}}{n_{60}}=\frac{60}{60}=1_{}$   (9)

In terms of volumes (V), the conversion rates of the different versions are:

$\frac{\frac{V_{2\pi }{}_{(25)}}{sv}}{\frac{V_{2\pi }{}_{(60)}}{sv}}=\frac{n_{25}}{n_{60}}=\frac{25}{60}={0.416}_{}{;}_{}\frac{\frac{V_{2\pi }{}_{(30)}}{sv}}{\frac{V_{2\pi }{}_{(60)}}{sv}}=\frac{n_{30}}{n_{60}}=\frac{30}{60}={0.5}_{}{;}_{}\frac{\frac{V_{2\pi (60)}}{sv}}{\frac{V_{2\pi }{}_{(60)}}{sv}}=\frac{n_{60}}{n_{60}}=\frac{60}{60}=1_{}$   (10)

According to them, in the case of the time dimension (t) and three spatial dimensions (V) assigned to the number of heart contractions, the result and the conversion rate are similar.

By multiplying the basic unit blood volume (stroke volume, sv) by the dimensionless heart contraction number (n), the blood volume can be increased to infinity. Specifically, in this case, the amount of blood (V_2π) will be as follows:

$V_{2\pi }=n\cdot sv=25\cdot 70ml=1750ml=1.75L$   (11)

If we assign a time dimension to this spatial dimension, i.e. we relate the volume to a time interval, we can talk about the blood volume per time unit. Moreover, considering the previous case (Eq.2, left), which is better known from medical physiology, the data concerning the intensity of the flowing fluids (I) corresponds to the volume (V) per unit time (t). This value is essentially the same as the concept of cardiac output (CO) determined on the basis of blood circulation tests. Intensity as a physical parameter corresponds to the value known from cardiology as minute volume (I ≈ CO),¹³ also with regard to the same dimensions.

The law of intensity, which corresponds to the cardiac output in medicine, is equal to the product of the heart rate, which is variable and the stroke volume, which is essentially unchanged (CO=n∙sv). Since the heart rate implicitly contains the time interval to which it is applied, different values are obtained depending on its value. In this way, the blood volume per minute, i.e., the minute volume, is 4.2 liters/minute (60/minute x 70 ml=4200 ml/minute) for a heart rate of 60. However, this volume value may change if the data is applied for half a minute or 25 seconds. The circulating blood volume (CO) for 25, 30 seconds or 1 minute is therefore the following:

$\begin{array}{l}{I}_1=\frac{V_{2\pi }}{t_{2\pi (25s)}}=C{O}_{25s}=\frac{n_{25}\cdot sv}{t_{2\pi (25s)}}=\frac{25\cdot {70}_{}ml}{t_{2\pi (25s)}}=\frac{1750ml}{t_{2\pi (25s)}}=1750ml/25s=1.75L/25s_{},\\ and:\\ I_2=\frac{V_{2\pi }}{t_{2\pi (30s)}}=C{O}_{30s(1/2\min )}=\frac{n_{30}\cdot sv}{t_{2\pi (30s)}}=\frac{30\cdot {70}_{}ml}{t_{2\pi (30s)}}=\frac{2100ml}{t_{2\pi (30s)}}=2.1L/0.5{\min }_{},\\ moreover:\\ I=\frac{V_{2\pi }}{t_{2\pi (60s)}}=C{O}_{1\min }=\frac{n_{60}\cdot sv}{t_{2\pi (60s)}}=\frac{60\cdot {70}_{}ml}{t_{2\pi (1\min )}}=\frac{60\cdot 70ml}{\text{1}\min }=\frac{4200ml}{\text{1min}}=\text{4}.2L/1\min \end{array}$   (12)

The first two CO values increase when projected at a heart rate of 60/min, the third remains unchanged. By dividing each CO by the ratio 25s/60s=0.41666 and 30s/60s=0.5 and 60s/60s=1, the result will be 4.2 L/min respectively (1.75 L/min/0.4166=4.2 L/min, 2.1 L/min/0.5=4.2 L/min, 4.2 L/min/1=4.2 L/min).

Projecting these CO values onto a heart rate of 72 contractions in 60 seconds, i.e., with a heart rate of 72/1minute, considering their ratios (25/72=0.3472, 30/72=0.4166, and 60/72=0.8333), the CO value will be higher than the previous one (Eq.5). In this way, the output of the heart will be 1.75L/0.3472=5.04 L/min and 2.1L/0.4166=5.04 L/min, as well as 4.2L/0.833=5.4 L/min, which agrees with our knowledge of cardiology.¹⁴

These are well-measurable but variable quantities, which can increase significantly under submaximal physical load (6-8 L/min). In case of an extreme degree of load, which means an increase in static or dynamic work performed against the gravitational field, the work of the heart and the related performance increase. After reaching a limit value, CO reaches its highest value in case of maximum heart rate. In the case of a relatively young adult male long-distance runner (from a starting value of 42-45/min), if the heart rate increases to a value of 170-175/min, the CO is as follows: 25s/170=0.147, 30s/170=0.1764, 60s/170=0.3529, therefore 1.75L/min/0.147=11.9L/min, 2.1L/min/0.1764=11.9, 4.2L/min/0.353=11.9 L/min.

Cross-sectional area and flow velocity of average human blood circulation

However, cardiac output is only a special value that does not express the quantitative parameters and qualitative characteristics of the complete human blood flow. Therefore, this should be supplemented, the following considerations are necessary.

When determining the cross-sectional area of an average human circulation with a circular shape and a circular cross-sectional area (A), the following data (V, t, s and v) shall be taken into account. Based on Eq. 2, taking the single circulation time (t_2π(25)) as 25 s,¹⁵ the circular cross-sectional area (A) of the average circulation is as follows:

$\begin{array}{l}Since:s_{2{\pi }_{}}=v\cdot t_{2\pi }{}_{},{{\displaystyle }}_{}and:{{\displaystyle }}_{}{V}_{2\pi }=A\cdot s_{2\pi }{}_{},\\ so:V_{2\pi }=A\cdot v\cdot t_{2\pi }{}_{},{{\displaystyle }}_{}therefore:{{\displaystyle }}_{}A=\frac{V_{2\pi }}{v\cdot t_{2\pi }}\end{array}$   (13)

Another way to determine the intensity of blood flow is to use the law of continuity. The law of continuity of flowing fluids, which is another obligatory law, gives intensity (Eq.2 right side) as the product of the flow cross section area (A) and the flow rate (v). However, neither the cross-sectional area through which the blood would flow nor its flow rate is known. The situation is further complicated by the fact that A and v can change, while the intensity remains unchanged. With a smaller cross-sectional area, the flow rate may increase, while with a larger cross-sectional area it may decrease (see also Bernoulli’s law). Therefore, since this flow formula contains two unknowns, in addition to knowing the flow intensity, the average flow velocity would be needed to calculate the average cross sectional area. Overall, in order to use both laws of flow, the average flow rate should be known.

One possible way to determine blood flow velocity is as follows. Given that the flow velocity in the capillaries is approximately 1 mm/s^16–18 and that the main artery (aorta) is 1m/s.^19,20 the average velocity should be somewhere in the middle, i.e., between cm and decimeter. A sufficiently accurate value can be determined with this symmetric (not based on an arithmetic mean) delimitation method that takes into account the extreme values of the circulation and moves from the outside towards the center. This average speed is therefore about 5 centimeters per second or 0.5 decimeters per second. The variability of the extreme values (e.g., 1.5 m/s in the aorta or 0.3 mm/s in the capillaries) does not significantly change this average value.

Calculating with the law of intensity, substituting the value of velocity (v_average), the average flow cross-sectional area (A₁) is as follows.

$A_1=\frac{V_{2\pi (25)}}{v\cdot t_{2\pi (25)}}=\frac{n\cdot sv}{v\cdot t_{2\pi (25)}}=\frac{25\cdot {70}_{}c{m}^3}{0.05\frac{m}{s}\cdot 25s}=\frac{1.75\cdot {10}^{-3}{}_{}{m}^3}{0.05\frac{m}{s}\cdot 25s}=1.4\cdot {10}^{-3}{}_{}{m}^2=14c{m}^2$   (14)

Even in the case of an increased blood volume (V_2π) in proportion to the single circulation time (t₃₀), the flow cross-sectional area (A₂) will be the same.

$A_2=\frac{V_{2\pi (30)}}{v\cdot t_{2\pi (30)}}=\frac{30\cdot {70}_{}c{m}^3}{0.05\frac{m}{s}\cdot 30s}=\frac{{2100}_{}c{m}^3}{5\frac{cm}{s}\cdot 30s}=\frac{2100c{m}^3}{150cm}=14c{m}^2$   (15)

Taking into account the law of continuity, by substituting the value of velocity (v_average), the average blood flow cross-sectional area (A) can be given as follows:

$I_{25}=A\cdot v_{},{{\displaystyle }}_{}so:{{\displaystyle }}_{}A=\frac{I_{25}}{v}=\frac{1.75\cdot {10}^3\frac{c{m}^3}{25s}}{5\frac{cm}{s}}=\frac{1750\frac{c{m}^3}{s}}{125\frac{cm}{s}}=14c{m}^2$   (16)

(The average cross-sectional area will also be similar /A₁=A₂/ in the case of the correspondingly increased flow intensity for 30 and 60 seconds.)

The length of the average blood circulation by knowing the circulation's single turnaround time

Based on the single circulation time of blood circulation (t_2π), which is 25-30 s, and its average flow speed (v_average), which is 5 cm/s, the length of the average circulation (s) can be determined:

$Since:{{\displaystyle }}_{}{V}_{2\pi }=A\cdot s_{2{\pi }_{}},{{\displaystyle }}_{}so:{{\displaystyle }}_{}{s}_{2{\pi }_{}}=\frac{V_{2\pi }}{A}=\frac{{2100}_{}c{m}^3}{14c{m}^2}=150cm$   (17)

Alternatively:

$s_{2{\pi }_{}}=v\cdot t_{2\pi }$   (18)

For a single turnaround time of 25 seconds, the tube length is as follows (see Eq.2):

$s_1=5\cdot {10}^{-2}m/s\cdot 25s={1.25}_{}m$   (19)

For a single turnaround time of 30 s, the tube length (s) is:

$s_2=5\cdot {10}^{-2}m/s\cdot 30s={1.5}_{}m$   (20)

It can be seen from this that the average length of blood circulation under physiological conditions at rest is between 1.25 m and 1.5 m.

The circumference and radius of the average blood circulation

For an average blood circulation of round and circular cross-section (torus), the circumference (C) and radius (r) are as follows:

$C=2\cdot r\cdot \pi {{\displaystyle }}_{},{{\displaystyle }}_{}so{{\displaystyle }}_{}{{\displaystyle }}_{}r=\frac{C}{2\cdot \pi }$   (21)

Since the perimeter (C₁) is equal to the length (s₁), the radius (r₁) of the torus is:

$r_1=\frac{s_1}{2\cdot \pi }=\frac{{1.25}_{}m}{6.2831853}={19.8943}_{}cm$   (22)

Since the circumference (C₂) is equal to the length (s₂), the radius (r₂) of the circle is:

$r_2=\frac{s_2}{2\cdot \pi }=\frac{{1.5}_{}m}{6.2831853}={23.8732}_{}cm$   (23)

The product of the two values (V₁=A∙s₁ and V₂=A∙s₂) also gives the mass of the blood (m), if we take the density (ρ) of blood to be the same as that of water for the sake of simplicity (m=ρ∙V).

The radius of cross-sectional area of the average blood circulation

In the case of average blood flow velocity (v=5cm/s) calculated on the basis of the extreme velocity values of blood circulation (Eq.14), the cross-sectional radius (r) of the average blood circulation is 2.11 cm, and its diameter is 4.22 cm.

The radius (r) of the cross-sectional area (A) of the circular tube, or torus, can be expressed from the relation A = r²∙π:

$A=r^2\cdot \pi {{\displaystyle }}_{},{{\displaystyle }}_{}so{{\displaystyle }}_{}{{\displaystyle }}_{}r=\sqrt{\frac{A}{\pi }}{{\displaystyle }}_{},{{\displaystyle }}_{}and{{\displaystyle }}_{}{{\displaystyle }}_{}d=2\cdot r=2\cdot \sqrt{\frac{A}{\pi }}$   (24)

The radius (r) and diameter (d) of the tube numerically:

$r=\sqrt{\frac{14c{m}^2}{3.141592}}={2.111}_{}cm{{\displaystyle }}_{},{{\displaystyle }}_{}and{{\displaystyle }}_{}{{\displaystyle }}_{}d=4.222cm$   (25)

Fractionation of the average blood circulation based on stroke volume and cross-sectional area

The amount of blood ejected during a single contraction of the heart, i.e., the stroke volume (sv), according to the ultrasound examination of the heart, is nearly 70 ml. With this blood volume, knowing the cross-sectional area (A) of the average blood circulation, the height (s) of the cylindrical part of the volume by which it moves in the direction of flow can be calculated. The volume can be divided into the product of the base area and the height of the cylinder that can be fitted into the torus. Thus, the amount of displacement of the blood circulation will be the ratio of the volume to the surface area (s=V/A), i.e., 70 cubic centimeters per 14 square centimeters, which corresponds to 5 cm. With this distance, the torus-shaped circulation model can be divided into minor units (n), which actually corresponds to the number of fractions per revolution of the circulation (t_2π). This number is 25, which also corresponds to the pulse.

The force of gravity affecting the average blood circulation

If the mass of blood (m₁), or in this case the volume of blood (V₁) is moved by the force of gravity (g) for a single revolution time (t_2π), then this force (F₁) is:

$F=m\cdot a=m_1\cdot g=V_1\cdot \rho \cdot g{{\displaystyle }}_{},{{\displaystyle }}_{}so{{\displaystyle }}_{}{F}_1={1.75}_{}kg\cdot {9.80665}_{}m\cdot s^{-2}={17.1616}_{}N$   (26)

Where mass (m₁) is the product of volume (V₁) and density (ρ) of the blood (m=V∙ρ; ρ≈1.060g/cm³). However, for the sake of simplicity, the density of blood is taken to be equal to that of water.

Moreover, for the larger volume (mass; m₂), the moving force (F₂):

$F_2={2.1}_{}kg\cdot {9.80665}_{}m\cdot s^{-2}={20.593965}_{}N$   (27)

The force driving the average blood circulation and its vertical, straightened dynamic version, which is a consequence of Earth's gravity, can vary between 17.1 N and 20.6 N in a resting state under physiological conditions. In the case of a force requiring the movement of a larger blood mass, i.e., when the circulation's single rotation time increases to 40, 50 or 60 seconds, the pressure would rise to such an extent that the cardiovascular system could not withstand it without damage.

The pressure conditions established by the gravitational force in the average blood circulation

The pressure (P) exerted by the force (F) on a unit area (A) in the case of the average human circulation is as follows:

$P_1=\frac{F_1}{A}=\frac{17.1616N}{0.0014m^2}={12258.2857}_{}N/m^2$   (28-a)

In the case of the larger moving force (F₂) and the same pipe cross-sectional area (A) the driving force (F₂) is as follows:

$P_2=\frac{F_2}{A}=\frac{20.593965N}{0.0014m^2}={14709.975}_{}N/m^2$   (28-b)

Since: 1 N/m² = 7.5 •10^-3 mmHg, in the case of the smaller driving force (F₁), the value of the pressure (P₁) in the average circulation is:

$P_1={12258.2857}_{}N/m^2\cdot 7.5\cdot {10}^{-3}=91937.14\cdot {10}^{-3}{}_{}\text{mmHg}\approx {92}_{}\text{mmHg}$   (29-a)

Moreover, in the case of a greater physiologic driving force (F₂), the value of the pressure (P₂) in the circulation will increase:

$P_2={14709.975}_{}N/m^2\cdot 7.5\cdot {10}^{-3}=110324.8125\cdot {10}^{-3}\text{mmHg}\approx {110}_{}\text{mmHg}$   (29-b)

Depending on the individual parameters (F, A), the pressure (P) in the average human circulation can take any value between 92 mmHg and 110 mmHg. Calculated with a simple mathematical average (101mmHg), this corresponds to 120 mmHg systolic and 80 mmHg diastolic data (or, in another variation, a blood pressure of 125/75 mm Hg). The latter higher average pressure (110mmHg) corresponds to the upper limit of normal blood pressure, i.e., blood pressure of 135/85 mmHg. These values correspond to the physiological measurement data determined by the invasive internal catheter method or by indirect external blood pressure detection.²¹

Gravitational work performed during a single rotation of the average blood circulation

The engine of the toroidal average human circulation is the function of the heart pump, which is, in a figurative sense, the equivalent of the driving force of gravity in the human body. The work required to maintain the flow (W₁) is the product of the force (F₁) and the blood flow length (s₁):

$W_1=F_1\cdot s_1=17.1616N\cdot 1.25m={21.452}_{}Nm={21.452}_{}J$   (30-a)

In the other case, when the greater force prevails (F₂), the amount of work (W₂) increases:

$W_2=F_2\cdot s_2={20.593965}_{}N\cdot 1.5m={30.5967}_{}Nm={30.8909}_{}J$   (30-b)

Therefore, the work of the heart maintaining the average human blood circulation, which is equivalent to the work of the gravitational attractive force, can vary between 21.4 J and 30.9 J at rest under physiological conditions.

The output of the heart for a single circulation time of the average blood circulation

The performance of the heart can be determined based on the estimation of the two extreme values of the maximum and minimum circulation speed (in the aorta and capillaries) existing in the human body. This limited average value (5 cm/s), approximated from above and below towards the center, can then be applied to the time of one turn (t₁=25 and t₂=30 sec) [2,15]. In this way, the power (P_1(watt)) of the work (W₁) of the driving force (F₁) required to maintain the average blood flow velocity (v_average) is:

$P_{1(watt)}=\frac{m_1\cdot g\cdot s_1}{t_{2\pi (25)}}=\frac{F\cdot s_1}{t_{2\pi (25)}}=\frac{W_1}{t_{2\pi (25)}}=\frac{{17.1616}_{}kg\frac{m}{s^2}\cdot 1.25m}{25s}=\frac{21.452Nm}{25s}={0.858}_{}J/s={0.858}_{}W$   (31-a)

(Since 1 kg·1 m²·1 s^‒2 = 1 J, and 1 Joule per second [J/s] = 1 Watt /W/.)

In the other case, with higher work (W₂) but higher single turaround flow time (t_2π(30)), the power (P_2(watt)) decreases slightly.

$P_{2(watt)}=\frac{W_2}{t_{2\pi (30)}}=\frac{{20.593965}_{}J}{{30}_{}s}={0.6864}_{}W$   (31-b)

Moreover, the output for a single heart contraction (t_1contraction) at average circulatory velocity (v_average), aortic blood flow speed (v_aorta), and capillary blood flow rate (v_capillary) is as follows:

$\begin{array}{l}{P}_{1(watt)}=\frac{m_{sv}\cdot g\cdot s_1}{t_{2\pi (25)}}=m_{sv}\cdot g\cdot v_{average}=0.07kg\cdot 9.80665\frac{m}{s^2}\cdot 0.05\frac{m}{s}=0.03432\frac{kg{m}^2}{s^3}=0.03432\frac{J}{s}\approx {0.034}_{}{W}_{},\\ but:\\ P_{1(watt)}=\frac{m_{sv}\cdot g\cdot s_1}{t_{2\pi (25)}}=m_{sv}\cdot g\cdot v_{aorta}=0.070kg\cdot 9.80665\frac{m}{s^2}\cdot 1.5\frac{m}{s}=1.02969J/s\approx {1.03}_{}{W}_{},\\ and:\\ P_{1(watt)}=\frac{m_{sv}\cdot g\cdot s_1}{t_{2\pi (25)}}=m_{sv}\cdot g\cdot v_{capillary}=0.070kg\cdot 9.80665\frac{m}{s^2}\cdot 0.001\frac{m}{s}={0.000686}_{}W\end{array}$   (32-a)

These are therefore speed-dependent values and indicate how much the heart's performance is at certain sections of the vascular path in relation to a single circulation period of the blood flow. At the average circulation speed (5 cm/s), the power per total circulation time is medium, between the power of a single contraction of the heart²¹ and the power in the capillaries.

However, performance (P_watt) relative to average circulation time (t_2π) for average circulation (v_average) and aortic (v_aorta) and capillary vasculature flow rates (v_capillary) is as follows:

$\begin{array}{l}{P}_{1(watt)}=\frac{V_{2\pi (25)}}{t_{2\pi (25)}}=\frac{n_{25}\cdot m_{sv}\cdot g\cdot s_1}{t_{2\pi (25)}}=25\cdot m_{sv}\cdot g\cdot v_{average}=25\cdot 0.07kg\cdot 9.80665\frac{m}{s^2}\cdot 0.05\frac{m}{s}=0.858\frac{kg{m}^2}{s^3}={0.858}_{}{W}_{},\\ but:\\ P_{1(watt)}=\frac{V_{2\pi (25)}}{t_{2\pi (25)}}=\frac{n_{25}\cdot m_{sv}\cdot g\cdot s_1}{t_{2\pi (25)}}=25\cdot m_{sv}\cdot g\cdot v_{aorta}=25\cdot 0.070kg\cdot 9.80665\frac{m}{s^2}\cdot 1.5\frac{m}{s}=\text{25}{\text{.74225}}_{}{W}_{},\\ and:\\ P_{1(watt)}=\frac{V_{2\pi (25)}}{t_{2\pi (25)}}=\frac{n_{25}\cdot m_{sv}\cdot g\cdot s_1}{t_{2\pi (25)}}=25\cdot m_{sv}\cdot g\cdot v_{capillary}=25\cdot 0.070kg\cdot 9.80665\frac{m}{s^2}\cdot 0.001\frac{m}{s}={0.01716}_{}W\end{array}$   (32-b)

In contrast to the previous ones (Eq.32.a), due to the relatively low speed of the average blood circulation (5 cm/s), the power per one revolution of the circulation (t_2π) will be similar to the power of a single contraction of the heart (t_1contraction). At the flow rate of the aorta and capillaries, the performance would be so high without fractionation that the heart would not be able to perform this and the capillary system would be damaged.

Based on the physical hemodynamic parameters defined so far, the following average human blood circulation model can be developed.

Figure 2 The figure shows a torus-shaped representation of the average human blood circulation. The individual parameters /radius (r), volume (V), cross-section area (A), force (F), work (W), press (P_mmHg), power (P_watt)/ were determined from the velocity of the average circulation (v_average), as well as from the time (t_2π=25s-30s) and distance data (C =1.25m-1.5m) determined by circulation testing procedures.

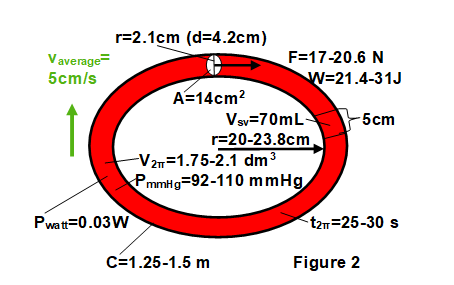
Figure 2 The figure shows a torus-shaped representation of the average human blood circulation.

The above data refer to the average human blood circulation as a whole. The time interval of the systemic and pulmonary circulation (t_2π,systemic=25s and t_{2π,pulmonary}=4s) can be accurately determined with the circulation testing procedures known from medical physiology in different ways, but with tests leading to similar results, such as with dye or heat dilution, as well as with radioisotope methods. Based on the closely related circulating blood volumes (V_2π,systemic and V_{2π,pulmonary}), as well as the speed of the average human blood circulation (v_average), a small and large blood circulation, which ensures a continuous one-way blood flow, can be distinguished. In possession of these data, the originally single round blood flow can be separated into two separate ones, which represent the blood circulation in refined detail.

Separation of pulmonary and systemic circulation

If we extract a section from the torus-shaped average human blood circulation, the length of which decreases in proportion to the circulation time (t_2π), the intensity does not change with the same flow cross-sectional area (I=A∙v).

The size (s, C) resulting from the single circulation time (t_2π,torus) and average speed of the blood circulation (v_{average,torus}) also includes the pulmonary circulation (t_pulmonary,s_pulmonary,v_{average pulmonary}). By subtracting the length (s_pulmonary) and volume of the pulmonary circulation (V_pulmonary) from the length (s_torus) and volume of the average human circulation (V_average), we obtain the length and volume of the systemic average circulation (C _systemic = C _torus – C _pulmonary and V_2π,systemic = V_2π,torus - V_{2π,pulmonary}). In this way, by separating the toroidal blood flow into two parts, a pulmonary and a systemic circulation, the highest degree of Darwinian evolution is realized, which culminates in the human circulatory system.

Similar to the toroidal average circulation, the velocity and cross-section of the pulmonary circulation should be considered similar (v = 5 cm/s and A = 14 cm²). This is necessary for the law of continuity to apply. If this law did not work, disturbances would occur in the cardio-pulmonary system and various disease states and related disease symptoms would occur.

In this way, knowing the time of pulmonary circulation (t_{2π,pulmonary}=3.98-4.47-4.67s).^22,23 which means the time of blood flow from the right ventricle to the left atrium (C_pulmonary), the length (s), radius (r) and cross sectional area (A) of the average pulmonary circulation can also be determined.

Figure 3 Representation of the average human blood circulation in the form of a "double torus", which approximately shows a ratio of six times or one sixth in relation to each other in terms of their various parameters. The figure shows the distribution of the blood volume per cycle (V_pulmonary = 0.28dm³ and V_systemic = 1.4-1.8 dm³) in proportion to the circulation times (t_{2π,pulmonary} = 4s and t_2π,systemic = 21-26s). This blood flow model, which can also be called the "folded figure of eight", shows unique parameters /radius (r), circumference (C), volume (V), cross-sectional area (A), force (F), work (W), pressure (P_mmHg), power (P_Watt)/ for both blood circuits, i.e., the pulmonary and systemic blood circuits. These are consistent with data from medical circulation testing procedures and clinical heart ultrasound (echocardiography) studies.

Figure 3 Representation of the average human blood circulation in the form of a "double torus", which approximately shows a ratio of six times or one sixth in relation to each other in terms of their various parameters.

Based on the two blood volumes, these average blood pressure values persist between 77.2 mmHg and 95.6 mmHg. In a state of rest, in the case of physiological conditions, any value between the two values can exist. These correspond approximately to blood pressure values of 92/62 mmHg and 120/70 mmHg, which are also limit values. In cases lower than the former, we can talk about hypotonic states of various origins, and in cases higher than the latter, we can talk about incipient hypertension.²¹

Parameters of the average pulmonary circulation

Similar to the above, the two obligatory flow laws apply to the average pulmonary circulation the path of circulating blood:

$\begin{array}{l}\frac{A\cdot s}{t_{2\pi }}=A\cdot v,{{\displaystyle }}_{}{{\displaystyle }}_{}so:{{\displaystyle }}_{}\frac{s_{pulmonary}}{t_{2\pi (pulmonary)}}=v_{average}{}_{},{{\displaystyle }}_{}and{:}_{}{{\displaystyle }}_{}{s}_{pulmonary}=v_{average}\cdot t_{2\pi (pulmonary)}{}_{},\\ as:{{\displaystyle }}_{}{s}_{pulmonary}=C_{pulmonar{y}_{}circumference}{}_{},{{\displaystyle }}_{}{C}_{pulmonar{y}_{}circumference}=5\frac{cm}{s}\cdot 4s={20}_{}cm\end{array}$   (33)

From the length of the pulmonary circumference (C_{pulmonary circumference}), the radius of the pulmonary circulation (r_{pulmonary circulation}) is as follows:

$C=2\cdot r\cdot {\pi }_{}{,}_{}so{{\displaystyle }}_{}{r}_{pulmonar{y}_{}circulation}=\frac{C_{pulmonar{y}_{}circumference}}{2\cdot \pi }=\frac{\text{20}cm}{\text{6}\text{.283184}}=\text{3}\text{.1831cm}$   (34)

The magnitude of the average systemic circulation can be determined by subtracting the length of the pulmonary circulation from the toroidal circulation:

The length of the average systemic circulation (Eq.73) in the figure-8 circulation model based on the length of the larger average toroidal circulation will be as follows:

$s_{averagehumancirculation2}-s_{averagehumanpulmonar{y}_{}circulation}=s_{averagehumansystemi{c}_{}circulation2}=1.5m-0.2m=\text{1}\text{.3}m$   (35-b)

The volume (V_pulmonary ≈ m_pulmonary) of blood (in the figure-8 circulation) passing through the smaller cross-section in the average pulmonary circulation expressed in kilograms is as follows:

$V_{pulmonary}=A_{pulmonary}\cdot s_{pulmonar{y}_{}circulation}=0.0014m^2\cdot 0.2m=\text{0}{\text{.00028}}_{}{m}^3\approx \text{0}{\text{.28}}_{}k{g}_{}$   (36)

Since this mass (m) is moved by gravity (g) along the circumference (s, C), the force (F):

$F=m\cdot a=m\cdot g{{\displaystyle }}_{},{{\displaystyle }}_{}so{{\displaystyle }}_{}{{\displaystyle }}_{}{F}_{pulmonary}={0.28}_{}kg\cdot 9.80665m\cdot s^{-2}=\text{2}{\text{.74586}}_{}N$   (37)

The pressure (P_pulmonary) in the pipe is based on the force (F) acting on the surface (A) as follows:

$P_{pulmonary}=\frac{F_{pulmonary}}{A_{pulmonary}}=\frac{\text{2}\text{.74586}N}{0.0014m^2}={1961.33}_{}N/m^2$   (38-a)

Since 1 N/m² = 7.5∙10^-3 Hgmm, the pressure in the average human pulmonary circulation, expressed in millimeters of mercury:

$P_{(mmHg)pulmonary}=1961.33\cdot 7.5\cdot {10}^{-3}mmHg={14.71}_{}\text{mmHg}$   (38-b)

Thus, according to our current knowledge, under physiological conditions, at rest, the average pulmonary pressure is 14.7 mmHg.²⁴  

Outstanding parameters of the average systemic circulation

On the other hand, the volume values of the average systemic circulation (V₁ and V₂) are numerically as follows:

$\begin{array}{l}{V}_{1systemi{c}_{}circ.}=A_{systemic}\cdot s_{1systemi{c}_{}circ.}=0.0014m^2\cdot 1.05m=\text{0}\text{.00147}{m}^3\approx {1.47}_{}k{g}_{},\\ and:\\ V_{2systemi{c}_{}circ.}=A_{systemic}\cdot s_{2systemi{c}_{}circ.}=0.0014m^2\cdot 1.3m=\text{0}\text{.00182}{m}^3=1.82kg\end{array}$   (39)

The forces (F₁ and F₂) acting on the average systemic circulation are as follows:

$\begin{array}{l}{F}_{1systemi{c}_{}circ.}=m\cdot a=m_{1systemi{c}_{}circ.}\cdot g,{{\displaystyle }}_{}so{{\displaystyle }}_{}{F}_{1systemi{c}_{}c.}=1.47kg\cdot 9.80665m\cdot s^{-2}=\text{14}{\text{.4158}}_{}N,\\ but:\\ F_{2systemi{c}_{}circ.}=m\cdot a=m_{2systemi{c}_{}circ.}\cdot g,{{\displaystyle }}_{}so{{\displaystyle }}_{}{F}_{2systemi{c}_{}c.}=1.82kg\cdot 9.80665m\cdot s^{-2}=\text{17}{\text{.8481}}_{}N\end{array}$   (40)

In the systemic average circulation, the pressures (P_{systemic circulation1} and P_{systemic circulation2}) created as a result of the forces (F_{systemic circulation1} and F_{systemic circulation2}) moving smaller and larger masses on the given cross-sectional area (A) are as follows:

$\begin{array}{l}{P}_{systemi{c}_{}circulation1}=\frac{F_{systemi{c}_{}circulation1}}{A_{systemic}}=\frac{\text{14}{\text{.4158}}_{}N}{0.0014m^2}={10297}_{}N/m^2{{\displaystyle }}_{},\\ and\\ P_{systemi{c}_{}circulation2}=\frac{F_{systemi{c}_{}circulation2}}{A_{systemic}}=\frac{\text{17}{\text{.8481}}_{}N}{0.0014m^2}=\text{1}{2748.643}_{}N/m^2\end{array}$   (41)

Since 1N/m² = 0.007501 mmHg, the pressure (P_{mmHg systemic circulation1}) is expressed in millimeters of mercury:

$\begin{array}{l}{P}_{systemi{c}_{}circulation1}=10297\cdot 7.5\cdot {10}^{-3}mmHg\text{ = 77}{\text{.227}}_{}mmHg{{\displaystyle }}_{},\\ and\\ P_{systemi{c}_{}circulation2}=\text{1}2748.643\cdot 7.5\cdot {10}^{-3}mmHg={95.615}_{}mmHg\end{array}$   (42)

These systemic average human blood pressure values, based on the two blood volumes (masses), are between 77.2 mmHg and 95.6 mmHg. This also means that they can take any value between the two values under physiological conditions at rest. This corresponds approximately to blood pressure values of 95/60 mmHg and 120/70 mmHg. Blood pressure values above and below these are essentially limit values. Values that differ from this, measured at rest, are already pathological in nature; in these cases, we can talk about diseases of various origins, high blood pressure or hypotensive states.²¹

The difference between the average systemic and pulmonary circulation in the ratio of their parameters

The difference between the two average blood flow circles can be illustrated by comparing them. The ratio of the two shows the relationship between the parameters according to the following equation in close connection with the statements of Bernoulli's law. According to this, the work done by the contraction of both chambers of the heart (W) is proportional to the product of the pressure (P) in the two blood circuits and the blood volume (V) of the systemic and pulmonary circulation, as W=P∙V.

Since the blood volume (V) is proportional to the mass of the blood (m) or is essentially the same as it (m=ρ∙V; ρ≈1kg/dm³), simplifying with m and g, the equation is reduced to the ratio of the distance (s) traveled by the bloodstream:

$\begin{array}{l}\frac{P_{(mmHg)systemic}}{P_{(mmHg)pulmonary}}=\frac{\frac{W_{systemic}}{V_{systemic}}}{\frac{W_{pulmonary}}{V_{pulmonary}}}=\frac{\frac{F_{systemic}\cdot s_{systemic}}{V_{systemic}}}{\frac{F_{pulmonary}\cdot s_{pulmonary}}{V_{pulmonary}}}=\frac{\frac{m_{systemic}\cdot g\cdot s_{systemic}}{V_{systemic}}}{\frac{m_{pulmonary}\cdot g\cdot s_{pulmonary}}{V_{pulmonary}}}=\frac{\frac{m_{systemic}\cdot g\cdot s_{systemic}}{m_{systemic}}}{\frac{m_{pulmonary}\cdot g\cdot s_{pulmonary}}{m_{pulmonary}}}=\\ =\frac{s_{systemic}}{s_{pulmonary}}=\frac{1.3m}{0.2m}=6.5\end{array}$   (43)

By decomposing the volumes (V) in the formula into the product of the cross-sectional surface area (A) and the length of the tube (s) and then simplifying with A, g and s, only the ratio of the mass (m) of the two blood flow circuits remains:

$\frac{P_{(mmHg)systemic}}{P_{(mmHg)pulmonary}}=\frac{\frac{W_{systemic}}{V_{systemic}}}{\frac{W_{pulmonary}}{V_{pulmonary}}}=\frac{\frac{F_{systemic}\cdot s_{systemic}}{V_{systemic}}}{\frac{F_{pulmonary}\cdot s_{pulmonary}}{V_{pulmonary}}}=\frac{\frac{m_{systemic}\cdot g\cdot s_{systemic}}{A\cdot s_{systemic}}}{\frac{m_{pulmonary}\cdot g\cdot s_{pulmonary}}{A\cdot s_{pulmonary}}}=\frac{m_{systemic}}{m_{pulmonary}}=\frac{1.82kg}{0.28kg}=6.5$   (44)

By comparing the relationships in Bernoulli's law with those in the present model, we can make the following observations. Bernoulli's law states that for the same flow intensity (I=A∙v), the product of the flow tube cross-sectional area and the flow velocity is constant. For a varying flow cross sectional area (A), the flow velocities (v) vary (A₁∙v₁=A₂∙v₂). With a larger flow cross sectional area (A↑), the flow velocity is smaller (v↓) and vice versa, with a smaller flow cross sectional area (A↓) the velocity increases (v↑). The equality of flow intensities also corresponds to the law of conservation of energy, since the same volumes (V) pass through for the same periods of time (t) for any section of varying pipe cross-sectional area (A).

In the present model, in contrast to the above, the flow velocity is the same in both continuous blood circuits and the flow cross-sectional area does not change in them. In accordance with the conservation of energy, in this representation the mass and the associated volume, i.e., size, of the two blood circuits change with their associated pressures. The ratio is 6.5 according to the above formula. This means that the small mass moved by the right side of the heart is associated with a small force, which generates a small pressure for the same cross-sectional diameter. To move the larger mass of blood in the systemic circulation, the left side of the heart must exert a greater force, which is associated with a greater pressure for the same average cross-sectional area. This explains the difference in size and pressure between the two blood circuits. Accordingly, the pulmonary circulation is a low-pressure system, whereas the systemic circulation is a high-pressure system. The kinetic energy (E_kinetic=1/2 ρ∙v²) in Bernoulli's law is neglected in the model because of the low blood flow velocity (5cm/s). The difference in pressure due to the potential energy (E_potential=ρ∙g∙s) lies in the pressure due to the weight of the vertical blood column, calculated by the value of g, in both blood circuits that can be paralleled.

In the event of a positive or negative change in the above-mentioned size and pressure ratios, disturbances in the normal human circulation occur, physiological mechanisms become abnormal, and this leads to the development of various cardiovascular diseases.

Under physiological pressure conditions (P), the forces (F) driving the different masses (m) of the systemic and pulmonary circulation are proportional to each other:

$\begin{array}{l}\frac{P_{(mmHg)systemic}}{P_{(mmHg)pulmonary}}=\frac{\frac{F_{1systemic}}{A}}{\frac{F_{pulmonary}}{A}}=\frac{F_{1systemic}}{F_{pulmonary}}=\frac{\text{14}{\text{.4158}}_{}N}{\text{2}{\text{.74586}}_{}N}=5.25{{\displaystyle }}_{}{,}_{}or{{\displaystyle }}_{}\frac{\frac{F_{2syst.}}{A}}{\frac{F_{pulm.}}{A}}=\frac{F_{2systemic}}{F_{pulmonary}}=\frac{\text{17}{\text{.8481}}_{}N}{\text{2}{\text{.74586}}_{}N}={6.5}_{},\\ moreover:\\ \frac{P_{(mmHg)systemic}}{P_{(mmHg)pulmonary}}=\frac{\frac{F_{1systemic}}{A}}{\frac{F_{pulmonary}}{A}}=\frac{\frac{m_{1systemic}\cdot g}{A}}{\frac{m_{pulmonary}\cdot g}{A}}=\frac{m_{1syst.}}{m_{pulm.}}=\frac{{1.47}_{}kg}{0.28kg}=5.25{{\displaystyle }}_{},{{\displaystyle }}_{}or{{\displaystyle }}_{}\frac{m_{2syst.}}{m_{pulm.}}=\frac{{1.82}_{}kg}{0.28kg}=6.5\end{array}$   (45)

The pressure (P) established by the work of the heart (W) in the systemic and pulmonary blood circulation can be broken down into its components in the following steps. Since the flow cross-sectional areas (A) and flow velocities (v) are equal in both blood circuits, they drop out together with g. In this way, the formula is simplified and reduced to their blood volumes (masses; m), their dimensions (s), and their flow time (t):

$\begin{array}{l}\frac{P_{(mmHg)systemic}}{P_{(mmHg)pulmonary}}=\frac{\frac{W_{systemic}}{V_{systemic}}}{\frac{W_{pulmonary}}{V_{pulmonary}}}=\frac{\frac{F_{systemic}\cdot s_{systemic}}{A_{systemic}\cdot v_{systemic}\cdot t_{systemic}}}{\frac{F_{pulmonary}\cdot s_{pulmonary}}{A_{pulmonary}\cdot v_{pulmonary}\cdot t_{pulmonary}}}=\frac{\frac{m_{systemic}\cdot g\cdot s_{systemic}}{A_{systemic}\cdot v_{systemic}\cdot t_{systemic}}}{\frac{m_{pulmonary}\cdot g\cdot s_{pulmonary}}{A_{pulmonary}\cdot v_{pulmonary}\cdot t_{pulmonary}}}=\frac{\frac{m_{systemic}\cdot s_{systemic}}{t_{systemic}}}{\frac{m_{pulmonary}\cdot s_{pulmonary}}{t_{pulmonary}}}\\ =\frac{m_{systemic}\cdot \frac{s_{systemic}}{t_{systemic}}}{m_{pulmonary}\cdot \frac{s_{pulmonary}}{t_{pulmonary}}}=\frac{1.82kg\cdot \frac{1.5m}{30s}}{0.28kg\cdot \frac{0.2m}{4s}}=\frac{1.82kg\cdot 0.05\frac{m}{s}}{0.28kg\cdot 0.05\frac{m}{s}}=\frac{1.82kg}{0.28kg}=6.5\end{array}$   (46)

Moreover, based on the relationship v=s/t, knowing the flow distance and flow time, these can be converted into flow speed. In this way, the ratio of the pressures of the systemic and pulmonary circulations (P_systemic and P_pulmonary) is proportional to the product of their volume (mass) occupied in their circulation (m_systemic and m_pulmonary) and their velocity (v_systemic and v_pulmonary):

$\frac{P_{(mmHg)systemic}}{P_{(mmHg)pulmonary}}=\frac{m_{systemic}}{m_{pulmonary}}\cdot \frac{v_{systemic}}{v_{pulmonary}}=\frac{1.82kg}{0.28kg}=6.5$   (47)

Taking into account the velocities (v), which are the same in the two circulations, they drop out and only the mass (m) ratio remains.

As can be seen from Formulas 43 and 44, the pressure in both blood flow circuits of the model is directly proportional to the masses occupying them, which also determines their size. By applying the laws of flow, including the laws of intensity and continuity (I=V/t and I=A∙v), the diverse processes taking place in the human body can be simplified. However, for this, two flow factors (A and v) must be considered unchanged. As a result, the variable parameters culminate only in the mass (m) and its inseparable dimensions (s, C and r) located in the torus. In this way, the complex system of human blood circulation becomes more transparent by creating a model of the average human blood circulation.

Our basic goal in this article was to whether it is possible to establish a flow model for the entire human blood circulation, which is related to the weight of bodies due to gravity and the flow laws of physical fluids. Furthermore, by using or supplementing certain parameters of the intensity and continuity laws, is it possible to depict the entire human blood circulation, which reflects the objective data determined by medical examination procedures. The novelty in this flow system is a mass determined based on the weight of the blood column, which can be related to the gravity of the earth's surface and which provides a basis for determining the force that maintains blood circulation. The other pivotal point is the determination of an average blood flow velocity value in the human body, which can be used to calculate the size and cross-sectional area of the average blood circulation. In this way, a torus-shaped model can be set up and operated. By further refining the method, it is possible to create a double torus that passes into each other, or a geometric formation similar to a folded figure of eight. Each of its parameters confirms and satisfies the conditions for the functioning of the pulmonary and systemic circulation. Based on all of this, it is likely that the sophisticated, physically oriented systems of biology (Hagen–Poiseuille’s low, Frank–Starling law, Fick’s low, Laplace’s low, etc.) will merge into these flow-based physical laws.

None.

The author declares that the publication was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

None.

1. Faber TE. Physics, Fluid mechanics. Britannica; 2023.
2. Allsager CM, Swanevelder J. Measuring cardiac output. BJA CEPD Reviews. 2003;3(1):15–19.
3. Juncker M. How to Calculate Fluid Pressure. wikiHow; 2022.
4. Klabunde RE. Stroke Work and Cardiac Work. Cardiovascular Physiology Concepts; 2017.
5. Nordtvedt KL, Cook AH. Newton’s law of gravity. Encyclopedia Britannica; 2023.
6. Urone PP, Hinrichs R, Dirks K, et al. College Physics: OpenStax.  Flow Rate and Its Relation to Velocity. 2016.
7. Lund Johansen P. The dye dilution method for measurement of cardiac output. Eur Heart J. 1990;(Suppl I):6–12. 
8. Conway J, Lund Johansen P. Thermodilution method for measuring cardiac output. Eur Heart J. 1990;1(Suppl I):17–20.
9. Seldon WA, Hickie JB, George EP. Measurement of Cardiac Output Using a Radioisotope and a Scintillation Counter. Br Heart J. 1959;21(3):401–406.
10. Fouad Tarazi FM, MacIntyre WJ. Radionuclide methods for cardiac output determination. Eur Heart J. 1990;11(Suppl_I):3–40.   
11. Bruss ZS, Raja A. Physiology, Stroke Volume. National Library of Medicine; 2022.
12. Laskowski ER. What's a normal resting heart rate? Mayo Clinic; 2022.
13. Smith M. What Is Cardiac Output? WebMD; 2022.
14. Libby P, Zipes DP, Bonow RO, et al. Braunwald's Heart Disease: A Textbook of Cardiovascular Medicine. 6th ed; 1980.
15. Rakshitha C. Blood Circulation Time: Definition and Importance, Humans, Biology. Biology Discussion.
16. Ohnishi Y, Fujisawa K, Ishibashi T, et al. Capillary blood flow velocity measurements in cystoid macular edema with the scanning laser ophthalmoscope. Am J Ophthalmol.1994;117(1):24–29.
17. Merrikh AA, Lage José L. Effect of blood flow on gas transport in a pulmonary capillary. J Biomech Eng. 2005;127(3):432–439.
18. Hudetz AG. Blood flow in the cerebral capillary network: a review emphasizing observations with intravital microscopy. Microcirculation. 1997;4(2):233–252.
19. Gardin JM, Burn CS, Childs WJ, et al. Evaluation of blood flow velocity in the ascending aorta and main pulmonary artery of normal subjects by Doppler echocardiography. Am Heart J. 1984;107(2):310–319.
20. Garcia J, Roel LF, Bollache E, et al. Distribution of blood Flow velocity in the normal aorta: Effect of age and gender. J Magn Reson Imaging. 2018;47(2):487–498.
21. Fauci AS, Braunwald E, Kasper DL, et al. Harrison's Principles of Internal Medicine. 17th ed. New York: McGraw-Hill; 2011.
22. He Zhao, Jiaywei Tsauo, Xiaowu Zhang, et al. Pulmonary transit time derived from pulmonary angiography for the diagnosis of hepatopulmonary syndrome. Liver Int. 2018;38(11):1974–1981.
23. Slutsky RA, Bhargava V, Higgins CB. Pulmonary circulation time: comparison of mean, median, peak, and onset (appearance) values using indocyanine green and first-transit radionuclide techniques. Am Heart J. 1983;106(1 Pt 1):41–45.
24. Lau EMT, Godinas L, Sitbon O, et al. Resting pulmonary artery pressure of 21–24 mmHg predicts abnormal exercise haemodynamics. Eur Res J. 2016;47:1436–1444.