We report here a detailed 3-dimensional (3-D) electromagnetic (EM) simulation study on the feasibility of Wireless Power Transfer (WPT) using the strongly coupled magnetic resonance (SCMR) effect at 5.8 GHz for potential μm-scale biosensors applications. The tiny 110 μm x110 μm planar aluminum inductor coil is built on the silicon substrate as our miniaturized receiver coil, which has been designed and simulated by 3-D EM simulations and its EM data is consistent with the measured data from an advanced IBM/Global Foundries' 0.18 μm complimentary metal-oxide-semiconductor (CMOS) silicon-on-insulator (SOI) process technology. By using small relay coils for an optimized four-coil WPT system to reach the SCMR condition, EM simulations show that one can increase the wireless power transfer between the transmitter coil to the miniature receiver coil by about 300% to 400% over the traditional 2-coil inductive resonant system at the 5.8 GHz ISM band, making SCMR quite attractive for implantable bioelectronics and biosensors applications, such as on cochlear implants, capsule endoscopy and pacemakers. Our study features the smallest receiver coil (about 330 times smaller in area) than the previously reported smallest receiver coil used in inductive coupling for wireless power transfer.

Keywords: 3-d electromagnetic simulation; 5.8 ghz ism (industrial, scientific, and medical radio) band; Inductive power coupling; Resonant inductive coupling; Strongly coupled magnetic resonance; Wireless power transfer

WPT: Wireless Power Transfer; SCMR: Strongly Coupled Magnetic Resonance; CMOS: Complimentary Metal-Oxide-Semiconductor; SOI: Silicon-on-Insulator; RF: Radio-Frequency; SCMR: Strongly Coupled Magnetic Resonance; GHz: Sub-Gigahertz; ISM: Industrial Scientific and Medical; CMOS: Complimentary Metal-Oxide-Semiconductor; SOI: Silicon-On-Insulator

Inductive coupling has been studied for decades to realize efficient wireless power transfer (WPT). Typically the radio-frequency (RF) source drives a transmitting (TX) primary coil, creating a sinusoidally time-varying magnetic field, which induces a voltage across the terminals of a receiving (RX) secondary coil, and thus power is wirelessly transferred to the load. Two-coil inductive coupling is now routinely used to power up High-Frequency (HF) RF ID (Identification Card) tags and many commercial medical implantable devices, such as cochlear implants [1-3]. Wireless power transfer can also used in pacemaker where the primary coil is assumed to be on-body, while the secondary coil is assumed to be inside the human body and connected to a battery recharge system [4]. The experimental results shows that the power transfer efficiency is greater than 36.6 % by using WPT on the optimal coil configuration for capsule endoscopy [5]. Integrated implantable hearing devices such as cochlear implant can also benefit from efficient wireless power coupling between first and second coils [1,6]. Wireless powering of implantable devices can remove the need for bulky batteries, which may eliminate a serious health risk if periodic surgeries were to be needed to replace them. A common technique for increasing the voltage received by the load is to add a parallel capacitor to the secondary RX coil to form a resonant circuit at the operating frequency [3]. In 2007, Soljacic M et al. [3] experimentally demonstrated efficient non-radiative wireless power transfer over distances up to 8 times the radius of the coils using a 4-coil strongly coupled magnetic resonance (SCMR) system, and transferred 60 watts with ∼40% efficiency over distances in excess of 2 meters at around 10 MHz [7]. One would, therefore, expect a well-designed multi-coils inductive coupling WPT system with SCMR can extend the power transfer distance over the 2-coil system with the same power, at least at low MHz range [7]. Zhang et al. [8] & Kim et al. [9] analyzed the transfer characteristics of the WPT system architectures with multi-relay coils based on the circuit mode theory. Kim et al. [9] pointed out that either a coaxially arranged relay coil or a perpendicularly arranged relay coil can considerably improve the system power transfer efficiency. Zhong et al. [10] also analyzed the power transfer characteristics of multi-relay coils system using the circuit mode theory, where the coils are arranged coaxially, non-coaxially and circularly.

Recently, wireless power transfer is also being used at sub-gigahertz (GHz) frequency to capsule endoscope where compact self-resonant antennas are designed to realize the transcutaneous power transfer [11]. It is commonly believed that efficient WPT to implantable devices require RF transmission frequency in the low MHz range to avoid excess losses in tissues. Therefore, antenna sizes above a few cm are required, making implantable devices with integrated antennas inherently large and cannot be miniaturized further. However, recently, Poon A et al. [12] from Stanford University have convincingly shown that when the receiver dimension is much smaller than its depth inside the body, there exists an optimal frequency for WPT and this frequency is much higher and in the giga-Hertz (GHz) range [12]. In their work reported in [12] the receiver coil size is 2mm x 2mm on each side and it is a square copper loop, similar to the size of another impressive miniature RX coil design of 2mm x 2 mm by the same Stanford group that achieved a wireless power coupling of -33dB, very close to the theoretical WPT limit they calculated as at -31 dB [13]. This "Midfield" WPT proposed by [8] claims to enable miniature implantable sensors with millimeter sized coils at nearly any location in the body without batteries [14]. The same group has also shown by EM simulations that different body tissues may have an optimal frequency greater than 4 GHz for optimal WPT. Therefore, by considering higher GHz frequency range will reduce the implanted coil size, we have chosen the 5.8 GHz Industrial, Scientific and Medical (ISM) band frequency for our WPT system design for this study. In this work, however, we propose an even more miniaturized WPT system with a receiver coil of only 110 x 110 mm in size, which is ~330x smaller in area than the previously reported 2mm x 2mm RX coil by the Stanford's group. We kept the RX-TX distance at 1 mm to mimic the near-field scenario of an implantable device right underneath the skin. Note this distance may also be increased from 1 mm to 1 cm, depending upon the application of WPT for different medical devices.

In addition, we investigate a special case of inductive coupling, namely the 4-coil SCMR as proposed in [7,15] to improve WPT with two relay coils sandwiched between the TX-RX coils. In our previous work [15] we have achieved -26 dB power coupling for the 4-coil system with a miniature RX coil. We report here a more optimized 4-coil system that has achieved an impressive power coupling of -20.12 dB (i.e., ~ 1% WPT efficiency), which shows a 6-7 dB improvement over the traditional 2-coil system and also our previous work.

Two-coil resonant system design

WPT can be achieved by transferring the RF power over an air gap using coupled TX-RX coils in a resonant circuit. When two coils are tuned to be resonating at the same frequency, a highly efficient transfer of power can take place. The most common resonant transfer circuit consists of a series tuned transmitting circuit and a parallel tuned receiving circuit (i.e., the series-parallel system) as shown in Figure 1, where the on-chip load resistance of R4 = 232 Ω and R3 = 0.5 Ω (representing the minute trace resistance when the tiny receiver coil is placed on a silicon substrate as part of the integrated circuit, or a "chip") connect to an on-chip RX tuning cap C2. The system operates at the 5.8 GHz ISM band in our analysis. The designed two-coil system has a high Q TX coil of 3 mm in diameter, with 28 mm thick and 40 mm wide Cu metal, placed on the 1 mm thick FR4 substrate. The WPT efficiency depends on the coupling coefficient (k) between the two inductors and their quality factors (Q). Here k is dependent on the distance between the coils, the ratio of the sizes of the coils, the shape of each coil and the angle between them. The inductance L and quality factor Q simulations of the TX coil and the RX coil are performed in ANSOFT HFSS 3-D electromagnetic (EM) simulator by taking the silicon substrate model into account, which is similar to the substrate model of IBM/Global Foundries' 7RFSOI 0.18 mm CMOS SOI process that has high resistive silicon substrate of 50 µm in thickness. Here the RX coil is an on-chip planar inductor design mimicking the 7RFSOI design-kit inductor design on a lossy high resistivity silicon substrate with SOI to facilitate miniaturization in size and thickness for applications such as in cochlear implants. The L and Q values are extracted from the EM simulated Y-parameters using the equation 1 below [15,17]:

$$\begin{array}{l}L=\frac{IM(\frac{4}{Y_{11}-Y_{12}-Y_{21}+Y_{22}})}{\omega }\\ Q=\frac{IM(\frac{4}{Y_{11}-Y_{12}-Y_{21}+Y_{22}})}{RE(\frac{4}{Y_{11}-Y_{12}-Y_{21}+Y_{22}})}\end{array}$$ (1)

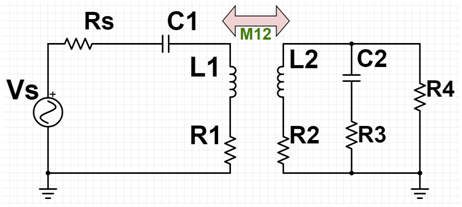
Figure 1: Series-parallel circuit model for our traditional 2-coil wireless power transfer (WPT) system.

where ω is the resonant frequency and IM and RE are the imaginary and real parts of the Y-parameter values, respectively. The simulated inductance of the TX coil design is 6.82 nH with a high Q of 67.2, as it can be fabricated off-chip with these feasible values. The RX on-chip planar inductor coil is on the realistic lossy silicon substrate and the complete stack design for the RX coil in IBM/GF 7RFSOI process is shown in Figure 2. The tiny 110 μm x110 μm planar aluminum inductor coil is built on the silicon substrate as our miniaturized receiver coil, which has been designed and simulated by 3-D EM simulations and its simulated EM data is found to be consistent when compared against the measured data from an advanced IBM/Global Foundries' 0.18 mm complimentary metal-oxide-semiconductor (CMOS) silicon-on-insulator (SOI) process technology. Series-parallel compensation architecture is chosen for the 2-coil resonant system used here. The circuit R’s and C’s are calculated knowing L’s and Q’s as shown from equations (2)-(7) [16]:

$C1=\frac{1}{L1\times {\omega }^2}$ (2)

$C_2=\frac{1}{L^2\times {\omega }^2}$ (3)

$RS=R1=\sqrt{L1/C1}/Q1$ (4)

$R2=\sqrt{L2/C2}/Q2$ (5)

$R4=\sqrt{L2/C2}\times Q2$ (6)

$K_{12}=M_{12}\times \sqrt{L1\times L2 }$ (7)

Figure 2: On-chip coil (RX coil) metal stack designed in IBM/GF 7RFSOI 0.18 μm SOI CMOS technology.

On the TX side, Vs in Figure 1 functions as an AC source. In a resonant system with high Q, this is a narrow band system with negligible high order harmonics under steady state. From [15,16], the input impedance can be easily shown as:

$Z_{in}=Rs+j\omega L1+\frac{1}{j\omega C1}+R1+Z_{re}$ (8)

Where Zre is the reflected impedance to the TX side from the RX side. Taking mutual inductance model into account, the reflected impedance in a series-parallel compensation WPT system is given by equations (9)-(10):

$$Z_{re}= \frac{{\omega }^2{M}_{12}^2}{j\omega L2+R2+\left[\frac{1}{j\omega C2}+R3\right]R4}$$ (9)

$$=\frac{{\omega }^2{M}_{12}^2}{j\omega L2+R2+\frac{R4\times \left[\frac{1}{j\omega C2}+R3\right]}{\frac{1}{j\omega C2}+R3+R4}}$$ (10)

Therefore, the power transferred from the TX side to the RX side with a load of 232 Ω is:

$P=\mathrm{Re}\left\{Z_{re}\right\}.I_1^2$ (11)

Where I₁ is the current in the primary circuit, i.e., on the transmitter (TX) side.

The series-parallel circuit model for the 2-coil system was simulated in the ANSOFT MAXWELL environment and also co-simulated with the ANSOFT SIMPLORER for the power transfer as shown in Figure 3.

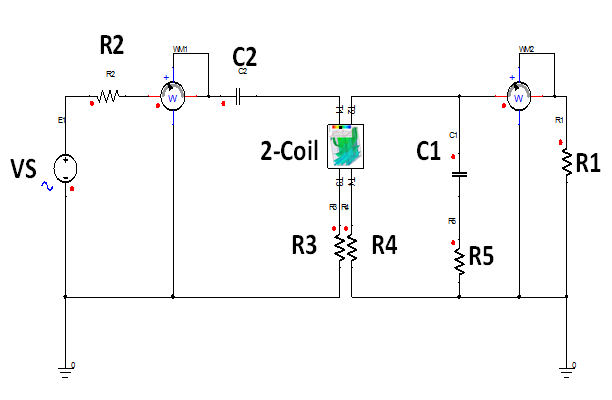
Figure 3: 2-coil coupling optimization in ANSOFT SIMPLORER co-simulated with HFSS/MAXWELL achieved with the tuning capacitors C1 and C2 at a coil-to-coil distance of 1 mm, where the RX coil inductance is 0.64 nH and R2=1.1 Ω; C2=0.110 pF; R3=1.1 Ω; L1=6.82 nH; R4=1.5 Ω; C1=1.05pF; R1=232 Ω (Load); R5=0.5 Ω.

Two-coil resonant system em simulation results

The tuning caps for the TX and RX coils help the entire traditional 2-coil WPT system shown in Figures 1 & 3 to resonate at 5.8 GHz. The simulated maximum power coupling of the 2-coil system is shown in Figure 4. Simulated mutual inductance for 2-coil system is M₁₂ = 2.81 pH and the k factor is calculated as $$k_{12}=\frac{M}{\sqrt{L1.L2}}$$ =0.001305. Parameters of two-coil system are shown in Table 1. The complete EM simulation stack of the 2-coil system is shown in Figure 4. The simulated wireless power coupling from the TX coil to the RX coil is -26.29 dB at the resonance frequency of 5.8 GHz.

The B-field of the designed traditional and optimized 2-coil WPT system was simulated in 3-D EM ANSOFT HFSS and its distribution plot is shown in Figure 6. Most region/space around the 2-coil system is green in color and its intensity ranges from 7.10 x 10^-4 T to 8.52 x 10^-4 T. We need to point out here that the SCMR condition as proposed in Reference [7] is not only for a 4-coil WPT system; it could also be reached for a traditional 2-coil WPT system if it satisfies the condition for strong magnetic coupling regime. The condition for strong coupling regime is $$\frac{k{\text{'}}^2}{{\Gamma }_A\times {\Gamma }_B}>1$$ , derived from the coupled mode (CM) theory [7]. The k’ and Γ are the coupling coefficient and the intrinsic decay rate, respectively, and they are functions of frequency from the CM theory as illustrated numerically below [7]:

$$\begin{array}{l}k\text{'}=\frac{\omega \text{M}}{\text{2}\sqrt{\text{L1}\times \text{L2}}}\\ \Gamma =\frac{\omega }{2Q}\end{array}$$

$\begin{array}{l}k\text{'}=\frac{\omega \text{M}}{\text{2}\sqrt{{\text{L}}_{\text{A}}\times {\text{L}}_{\text{B}}}}=\frac{2\pi \times 5.8\times {10}^9\times 2.81\times {10}^{-12}}{2\sqrt{0.68\times {10}^{-9}\times 6.82\times {10}^{-9}}}=2.4E7\\ {\Gamma }_A=\frac{\omega }{2Q_A}=\frac{2\pi \times 5.8\times {10}^9}{2\times 67.2}=2.71E8\\ {\Gamma }_B=\frac{\omega }{2Q_B}=\frac{2\pi \times 5.8\times {10}^9}{2\times 8.57}=2.12E9\\ =>\frac{k{\text{'}}^2}{{\Gamma }_A\times {\Gamma }_B}=\frac{{(2.4E7)}^2}{2.71E8\times 2.12E9}=1.04E-3<<1\end{array}$

Therefore, this 2-coil WPT system is NOT in the strongly magnetic coupled regime 1 mm away at 5.8 GHz.

Figure 4: 2-coil 3-D EM simulated wireless power coupling at a 1 mm TX-RX coil distance.

Figure 5: Our 2-coil system EM simulation setup in ANSOFT HFSS/MAXWELL.

Figure 6: 3-D EM simulated B-field of the designed 2-coil WPT system.

Four-coil scmr system design with em simulation results

The circuit for the corresponding 4-coil system design is shown in Figure 7. In this 4-coil system a series-parallel compensation architecture is used at the TX-RX sides similar to the 2-coil resonant system. The 2 relay coils, however, are inserted into the TX-RX coils to improve WPT without changing the TX coil and RX coil at all. Except for C1 and C2 that was also used in the 2-coil WPT system as shown in Figure 1, no tuning caps are used, especially no tuning cap for the 2 relay coils (i.e., the coils #2, #3 in Figure 7 sandwiched between the TX and RX coils). Other circuit component values in the TX and RX coils remain same as in the 2-coil system shown in Figure 1. Some key points we have found from EM simulations of the 4-coil system suggest that the parasitic resistance of the relay coils does not play a key role in this 4-coil system that has reached the SCMR condition, as will be described later. As we will show in this section, theoretical calculations using our EM simulated coupling data also indicates and confirms this optimized 4-coil SCMR system reaches the strongly coupled magnetic resonance regime, while the 2-coil system described earlier does not [7]. Neglecting the internal resistances for relay coils, the reflected impedance to TX side is given by equations (12)-(13):

$$R_{ref 2\to 1}= \left\{\frac{M_{12}^2}{M_{23}^2}\right\}\times R_{ref 3\to 2}$$ (12)

$R_{ref 3\to 2}= \left\{\frac{M_{23}^2}{M_{34}^2}\right\}\times R4$ (13)

Figure 7: Our optimized 4-coil SCMR series-parallel circuit model.

Each relay coil is 5 mm x 5 mm in size. As mentioned before, the TX coil in our 4-coil system is identical to the one shown in the 2-coil system with the same Q. The analytical analysis of the power transferred from TX coil to RX coil in this 4-coil SCMR system is more complicated than the 2-coil system and only the 3-D EM simulations data is shown below. The circuit is simulated in ANSOFT MAXWELL and co-simulated with ANSOFT SIMPLORER for wireless power transfer as shown in Figure 8.

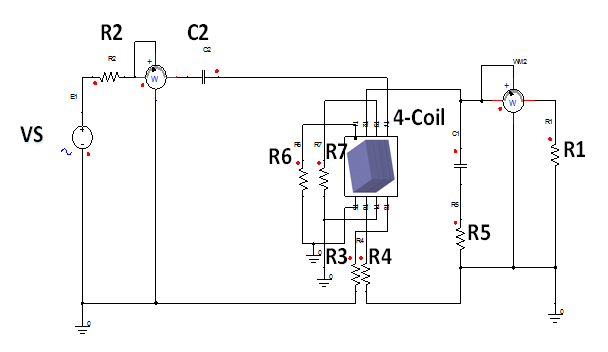
Figure 8: 4-Coil coupling SCMR optimization in ANSOFT SIMPLORER co-simulated with 3-D HFSS /MAXWELL achieved with the tuning capacitors C1 and C2 where the distance from the relay coil #3 to the RX coil is at 1 mm spacing and the self-inductance value of Coil #2 and #3 is both 7.86 nH. Here R2=1.1 Ω; C2=0.110 pF; R3=1.1 Ω; L1=6.82 nH; R4=1.5 Ω; L2=0.64nH; C1=1.21pF; R1=232Ω; R5=0.5Ω; R6=R7=19 Ω.

The RX coil used for the optimized 4-coil SCMR system has exactly the same stack as the 2-coil system. The dielectric between the Coil #1 and Coil #2, and Coil #2 and Coil #3 is also the same FR4 substrate and has a thickness of 0.3 mm each. The circuit elements of the 4-coil system are calculated similar to the 2-coil system that we have shown before. The power coupling of the 4-coil system is simulated in 3-D HFSS and the result is shown in Figure 9. The complete stack setup of the 4-coil system is shown in Figure 10. Parameters for the 4-coil SCMR system are shown in Table 2. From the data presented here, the optimized 4-coil SCMR system improves power coupling by ~6.1 dB vs. the corresponding optimized traditional 2-coil WPT system as shown earlier. The simulated Q of each of the relay coil is 12.72 and the coil inductance is 7.86 nH. Calculated resistance of the coil is 22.5 Ω by using Eq. 4. Even if the relay coil were to have a very low Q of 2.86, which corresponds to a large parasitic resistance of 100 Ω, the simulated power coupling for the SCMR 4-coil system would be -20.42 dB, which still has a ~6 dB higher power coupling than the corresponding optimized 2-coil system. Please note that even though there are two additional relay coils inserted for the 4-coil system, the losses introduced by them are very minimal according to the EM simulations and they not only do not degrade but actually enhance the power transfer efficiency for the optimized 4-coil SCMR system. These sophisticated EM simulations show promising data for practical implementation of our 4-coil SCMR system. Now we will show the calculations for the optimized 4-Coil WPT system to see if it has reached the SCMR condition:

$\begin{array}{l}k\text{'}=\frac{\omega \text{M}}{\text{2}\sqrt{{\text{L}}_{\text{S}}\times {\text{L}}_{\text{D}}}}=6.02E9\\ {\Gamma }_S={\Gamma }_D=\frac{\omega }{2Q_S}=\frac{\omega }{2Q_D}\frac{2\pi \times 5.8\times {10}^9}{2\times 12.72}=1.43E9\\ \frac{k{\text{'}}^2}{{\Gamma }_S\times {\Gamma }_D}=\frac{{(6.02E9)}^2}{{(1.43E9)}^2}=17.704>1\end{array}$  

$\begin{array}{l}k\text{1}=\frac{\omega \text{M}}{\text{2}\sqrt{{\text{L}}_{\text{S}}\times {\text{L}}_{\text{X}}}}=4.2E9\\ {\Gamma }_S=\frac{\omega }{2Q_S}=\frac{2\pi \times 5.8\times {10}^9}{2\times 12.72}=1.43E9\\ {\Gamma }_X=\frac{\omega }{2Q_X}=\frac{2\Pi \times 5.8\times {10}^9}{2\times 67.2}=2.71E8\\ \frac{k{1}^2}{{\Gamma }_S\times {\Gamma }_X}=\frac{{(4.22E9)}^2}{1.43E9\times 2.71E8}=46.08>1\end{array}$  

$\begin{array}{l}k\text{2}=\frac{\omega \text{M}}{\text{2}\sqrt{{\text{L}}_{\text{D}}\times {\text{L}}_{\text{Y}}}}=3.9E9\\ {\Gamma }_D=\frac{\omega }{2Q_D}=\frac{2\pi \times 5.8\times {10}^9}{2\times 12.7}=1.4E9\\ {\Gamma }_Y=\frac{\omega }{2Q_Y}=\frac{2\pi \times 5.8\times {10}^9}{2\times 8.5}=2.12E9\\ \frac{k{1}^2}{{\Gamma }_D\times {\Gamma }_Y}=\frac{{(3.9E9)}^2}{1.4E9\times 2.1E9}=5.1>1\end{array}$  

Therefore, our 4-coil WPT system (all coil couplings 1-2, 2-3, 3-4) is indeed in the SCMR regime according the calculations. Finally, the B-field of the optimized 4-coil SCMR system was simulated in 3-D EM simulation similar to the 2-coil system (Figure 6), and the result is shown in Figure 11. Most region/space around the 4-coil system is red in color and range from 1.56 x 10^-3 T to 1.70 x 10^-3 T, which is ~ 2x (or 6-7 dB) higher than the 2-coil case shown in Figure 6, suggesting the 4-coil system is indeed in a much strongly magnetically coupled regime, and the results are consistent with the SCMR calculations, and the ~6dB higher wireless power transfer from the S-parameter simulation data shown in (Figure 9).

Figure 9: Optimized 4-coil SCMR system 3-D EM simulated power coupling at 1 mm distance.

Figure 10: 4-coil SCMR system setup in ANSOFT HFSS/MAXWELL; TOP View (UP); Cross-section (DOWN).

We have presented an efficient and promising WPT design using near-field inductive 4-coil SCMR on a miniature RX coil at the 5.8 GHz ISM band. Both 3-D EM S-parameter simulation and the B-field simulations have shown the tuned 4-coil SCMR system achieves a ~ 6-7 dB improvement over the corresponding optimal 2-coil system for WPT, and this considerably higher power transfer is also accomplished at a larger separation distance between the TX coil and the RX coil (i.e., 1.6 mm for the 4-coil SCMR system vs. 1 mm for the 2-coil traditional system). Therefore, we conclude a well-designed 4-coil SCMR system should outperform the corresponding 2-coil system by successfully transferring about four times more power wirelessly into the tiny RX on-chip coil, which is about 330 times smaller in area than the previously reported smallest RX coil [12,13] for WPT using inductive coupling. We expect a power-efficient miniaturized SCMR WPT system has the potential to enable critical advancement in areas such as novel implantable and wearable biosensors and bioelectronics [14].

The authors would like to thank the funding support from the Keh-Shew Lu Regents Chair Endowment at Texas Tech, and Texas Instruments (TI) for the TI-Texas Tech Analog System and Design (ASD) program. We also like to thank Ms. D. Wang, Dr. Ned Cahoon, Dr. A. Joseph and Dr. D. Harame at IBM/Global Foundries for the 7RFSOI design kit access and collaboration.