In hyperthermia treatment for cancer, the antenna used as hyperthermia applicator needs to be designed carefully in order to heat the cancer cell without affecting the healthy cell. Unfortunately, as different antenna design produces different radiation pattern, it will lead to different heating distribution values. With these values, the time duration of the exposure for the cancer cell will also be different. In this research, the capability of a dipole antenna as hyperthermia applicator has been analyzed. The analysis has been done using simulation model in CST microwave simulation software based on FDTD technique. The result shows that the dipole antenna is deemed to be used as hyperthermia applicator. The heating pattern from the dipole antenna based on SAR distribution pattern shows that the focus area of the human tissues model, that has been designed using water bolus model has high Specific Absorption Rate (SAR) value compare to the surrounding area.

Keywords: hyperthermia, dipole antenna, SAR, FDTD technique, CST microwave studio

As cancer treatment technique, hyperthermia employs an outside, warm source to increase tissue temperature and slaughter cancer cells or impede their advance growth. The phrase 'hyperthermia' refers to several heat treatment procedures used in addition to other therapies.^1–4 These techniques provide high temperatures,^5–8 potentially causes direct damage to cancer cells compared to chemotherapy treatment with minimal or no harm to normal tissues and therefore this technique applied as an anti-drug for cancer treatment. The temperature of the hyperthermia treatment varies from 40^oC to 48^oC, and the heat temperature retained at the treatment area for one hour or more.⁸ In hyperthermia, the frequency that emits wavelengths equal to the size of the tumor in the human body that is of the most significant interest; however, government regulation influences the selection of frequency. The Federal Communications Commission in the United States, for Industry, Scientific and Medical (ISM) approve 915MHz and 2.45GHz; in Europe, 434MHz were mainly affirmed.⁹ In the case of different frequencies, a shielded or secure area should be used to avoid obstructions with a group of communications.

Future research is seeking to use this methodology to overcome some of the inherent limitations of radio frequency medical treatment devices. The design of the antenna is one of the known challenges in this approach, particularly when dealing in and near the patient’s body. This research work gives more clarity of the analysis of the interactions between biological tissues and microwave radiation, where it is very important in the design and functioning scheme of proposed antennas for microwave hyperthermia for the treatment of cancer. The production of the electromagnet (EM) wave in this treatment is based on antenna’s efficiency used known as hyperthermia applicator. As there are many types of antenna that can be used in producing the EM wave, the treatment time will be difference based on the antenna used. In determine the correct treatment time of the hyperthermia treatment, the antenna’s parameter need to be observed is the radiation pattern. In calculating this time in simulation model, the hyperthermia treatment simulation model can be designed using Finite Difference Time Domain (FDTD) technique. Then, as referring to the radiation pattern, Specific Absorption Rate (SAR) of an object can be calculated as the antenna simulation model can be updated by adding the object model in the simulation. As the SAR of an object is proportional to the object’s temperature, the value can be used to determine the treatment time of the hyperthermia treatment.¹⁰

The specific absorption rate, SAR is designed specifically for the measurement of EM wave radiation absorption in tissues and represents the amount of energy or power deposition per unit normal human tissue. As defined in equation (1), the value of the averaged local SAR was calculated as:

$SAR=\frac{{\left|E\right|}^2{\sigma }_e}{\rho }$

where Ε is the electric field strength (V/m), σ_e is the effective conductivity (S/m) and ρ is the mass density of the tissue (kg/m³).¹¹ In order to meet basic SAR restriction for general public exposure that use averaged method in IEEE/IEC 62704-1, three averaging mass or point SAR for SAR calculation such as 1g, 10g and point SAR has been introduced. Nonetheless, this research study only considers SAR calculation for 1g. For the most part, the averaged SAR calculation for 1g is less than 1.6W/kg as stated in IEEE Standard for safety levels for power delivered by the antenna that had to be altered.

Dipole antenna

The virtue of the dipole antenna is a reasonably low cost, lightweight and conveniently assembled.^12–15 The predominant geometry of the dipole antenna as hyperthermia applicator in this research is two wires that will work as a single wires’ antenna. Numerous parameters can be produced; however, in this research, it focuses on five basic parameters that need to be determined as listed in equation (2) until (5). Let resonant frequency, ƒ_r in Hertz (Hz) and speed of light, C = 3×10⁸ ms^-1, the wavelength of the EM wave can be calculated as:

λ₀ = C/ƒ_r

The length of the half-wave dipole antenna is calculated as:

L = λ₀ x 0.46

The calculation of the feeding gap of the antenna is:

Gap = L/200

The radius of the antenna is calculated as:

R= λ₀/1000

The length of the dipole antenna that is equal to a half-wavelength at the frequency of operation defines in a half-wave term. Besides, the dipole antenna is the basis for most antenna designs which is a balanced component with equal but opposite voltages and currents applied at its two terminals through transmission line.

Dipole antenna design for hyperthermia treatment with perfect electric conductor, pec material calculation

The half-wave dipole antenna has been designed at a resonant frequency 2.45GHz. The proposed design parameters of the half-wave dipole antenna have been simulated by using the CST Microwave Studio 2019 software. The design of the dipole antenna used in this study is as shown in Figure 1. The summary of the dipole antenna dimension designed in this study can be referred in Table 1. In order to design a hyperthermia applicator simulation model, the design dipole antenna of this research needs to be extended by adding a water bolus model in the simulation design. The aims of the simulation which is using the water bolus model as a material in the simulation techniques is to measure the SAR in the water bolus model. By this simulation, the heating value of the design antenna as hyperthermia applicator can be determined. The time exposure of the applicator could also be estimated based on this simulation. The design hyperthermia applicator model in this research is as shown in Figure 2 & Figure 3. In this research, the half-wave dipole antenna as hyperthermia applicator simulation model is designed by using the perfect electric conductor (PEC) and a water bolus model in cubic shape. The dimension of the normal water bolus model is 100mm x 100mm x 100mm for thick, high and width respectively. The epsilon value (permittivity) of the water is 78. The dynamic viscosity of the water bolus model is 1. Besides, it can be seen in Figure 3 that the electric conductivity of the water bolus model is 1.59S/m. The density of the normal water is 1000 kg/m³ while the thermal conductivity is 0.6 W/K/m. Furthermore, the heat capacity of the water bolus model is 4.2 kJ/k/kg while the diffusivity of the model is 0.000000142857m²/s.

Figure 1 The design of the half-wave dipole antenna in CST Microwave Studio 2019 software using PEC material.

Figure 2 A top view of half-wave dipole antenna as hyperthermia applicator simulation model in CST Microwave Studio Software.

Based on the reflection coefficient curve of dipole antenna of this research shown in Figure 4, the reflection parameter of the antenna at 2.45 GHz is about -55.762246dB. It can be seen that the reflection coefficient of this antenna has more exceptional performance as the functional return loss of an antenna should be at least -10dB. Again, by referring to this graph the antenna seems to do not have a mismatch issue because it begins at 0dB.The gain (IEEE) of the half-wave dipole antenna design in this study at 2.45 GHz as calculated in CST software is about 2.199dBi, as demonstrated in Figure 5. Besides, its radiation and total efficiency are about -0.01446dB and -0.01448dB respectively.

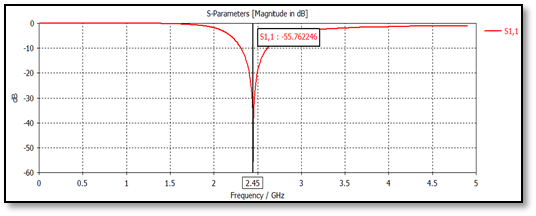
Figure 4 The reflection coefficient or return loss curve of half-wave dipole antenna simulation work at 2.45 GHz.

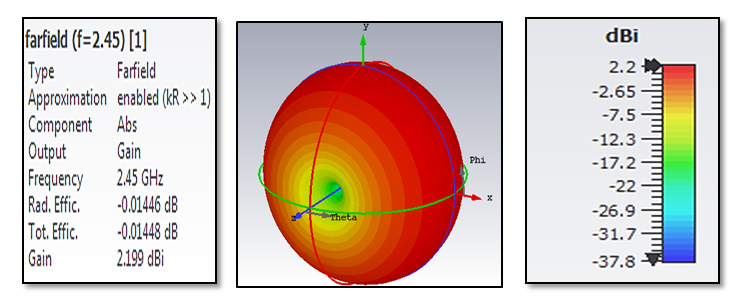
Figure 5 The far-field radiation pattern in gain (IEEE) output from dipole antenna simulation work at 2.45 GHz.

Results of dipole antenna as hyperthermia applicator

The far-field radiation pattern based on gain of the hyperthermia applicator of this study is estimated as 4.018dBi at 2.45 GHz. The maximum radiation can be seen in the red colour, and the minimum radiation in blue colour as shown in Figure 6. The radiated efficiency of this applicator is about -4.119dB and the total efficiency is about - 4.725dB. Comparing this radiation pattern to the half-wave dipole antenna’s radiation pattern, it can be observed that this hyperthermia applicator’s radiation pattern has directional pattern type which is towards the water bolus model. The maximum value of the radiation pattern has been increased for this applicator. The SAR which is used to measure the absorbed energy in water bolus by the hyperthermia applicator at 2.45GHz calculated in units of watts per kilogram using CST environment tools are as shown in Figure 7. The maximum SAR distribution value of this water bolus model viewed from the side is about 0.05 W/kg until 0.1 W/kg which fulfil the requirement of SAR level in 1g mass at 1.6W/kg or below. Most of the human tissue mainly consists of water, which contributes to high conductivity. Based on these results, the SAR values in this simulation work is said to depend on the distance of the hyperthermia applicator and the water model and also the conductivity value of the water.

Figure 6 3-Dimension far-field radiation pattern based on gain of hyperthermia applicator.

Figure 7 A side view of SAR distribution at 2.45 GHz in 1g averaging mass of half-wave dipole hyperthermia antenna in water model.

The distribution of SAR at top side of the water model in this simulation as based on 1g averaging mass is ranging from 0 W/kg until 17.6555W/kg. This value is higher than the FCC international standard that supposedly at and below than 1.6 W/kg at 2.45GHz as a protection value to the human body tissues. The maximum distribution value of the SAR in this side is more than the bottom side as shown in Figure 8, as this area’s distance is quite far from the antenna. Based on this figure, the SAR distribution at the bottom side of the water bolus model produced by the hyperthermia applicator is at minimum value of 0.01W/kg and maximum value of 0.1W/kg. The low value may also due to the conductivity value of the water. Figure 9 shows the 3-dimensional view of the SAR distribution of the water bolus model produced by the half-wave dipole antenna as hyperthermia applicator in hyperthermia applicator simulation model. As can be seem in this figure, the maximum value of the SAR distribution in 1g of the water bolus model produced by this hyperthermia applicator is about 17.6555 W/kg at 2.45GHz. In this simulation, the average cell mass used is about 0.00032338g. The SAR power in 1g mass of the water bolus model is about 0.26519 watt, while the average SAR power is about 0.002418219 W/mm³. Besides, the overall SAR value in 1g of this water bolus model exposed to the hyperthermia applicator is recorded as about 0.26519 W/kg which is following the averaging method in SAR calculation results in IEEE/IEC 62704^-1. Although the maximum SAR value of this water model exposed to the applicator is higher at the middle of the model, but the SAR value is less than 1W/kg in the surrounding area.

Figure 8 A top (left) and bottom (right) view: SAR distribution at 2.45 GHz in 1g averaging mass of half-wave dipole hyperthermia in water model.

Figure 9 SAR distribution of half-wave dipole hyperthermia antenna at 2.45 GHz in 1g averaging mass in water model.

Referring to the SAR calculation of the dipole antenna in this research, the SAR value in the middle of the water bolus model is higher which over the limit given by the FCC. Based on this SAR distribution pattern, it shows that the antenna will be able to heat the focus area efficiently which is in the middle of the water bolus model with less heating to the surrounding area. Based on this result, the dipole antenna design in this research can be said to be suitable to be used as hyperthermia applicator. As to improve this research in the future, the calculation of the heat produced by the SAR value of the dipole antenna can be determined. This will lead to the estimation of time of the hyperthermia treatment using the dipole antenna.

This research work under UTHM Postgraduate Research Grant (GPPS).

The author declares that there is no conflict of interest.

1. Nguyen PT, Abbosh AM, Crozier S. Realistic simulation environment to test microwave hyperthermia treatment of breast cancer. 2014 IEEE Antennas and Propagation Society International Symposium (APSURSI); Memphis, TN, USA. 2014. p. 1188–1189.
2. Xu Li, Bond EJ, Van Veen BD, et al. An overview of ultra-wideband microwave imaging via space-time beamforming for early-stage breast-cancer detection. In IEEE Antennas and Propagation Magazine; 2005;47(1):19–34.
3. Cappiello G, Margarethus M Paulides, Tomas Drizdal, et al. Robustness of Time-Multiplexed Hyperthermia to Temperature Dependent Thermal Tissue Properties. In IEEE Journal of Electromagnetics, RF and Microwaves in Medicine and Biology; 2020;4(2):126–132.
4. Huang C, Lin X, Lo W. Design and construction of a hyperthermia system with improved interaction of magnetic induction-heating. 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology; Buenos Aires, Argentina. 2010. p. 3229–3232.
5. Rotman R. Recent advances using microwaves for imaging, hyperthermia and interstitial ablation of breast cancer tumors. 2011 IEEE International Conference on Microwaves, Communications, Antennas and Electronic Systems (COMCAS 2011); Tel Aviv, Israel. 2011. p. 1–4.
6. Van Rhoon GC, Maarten M Paulides, Paolo Togni, et al. Challenges of the clinical application of hyperthermia for head and neck tumors. 2013 7th European Conference on Antennas and Propagation (EuCAP); Gothenburg, Sweden. 2013. p. 635–637.
7. Drizdal T, Paulides MM, Trujilo-Romero CJ, et al. Prediction of temperature distribution for superficial hyperthermia treatment: Accuracy of temperature dependent blood perfusion model. 2014 44th European Microwave Conference; Rome, Italy. 2014. p. 782–785.
8. Faridi P, Tej B Shrestha, Marla Pyle, et al. Temperature estimation for MR-guided microwave hyperthermia using block-based compressed sensing. 2020 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC); Montreal, QC, Canada. 2020. p. 5057–5060.
9. Singh T, Stevanovic MN, Kolundzija B. Survey and Classification of Antennas for Medical Applications. 2019 13th European Conference on Antennas and Propagation (EuCAP); Krakow, Poland. 2019. pp. 1–5.
10. IEC/IEEE Draft International Standard for Determining the Peak Spatial Average Specific Absorption Rate (SAR) in the Human Body from Wireless Communications Devices, 30 MHz - 6 GHz. Part 1: General Requirements for using the Finite Difference Time Domain (FDTD) Method for SAR Calculations. In P62704-1_D3, August 2016. 2016. p. 1–78.
11. Zhang HH, Yu GG, Liu Y, et al. Design of Low-SAR Mobile Phone Antenna: Theory and Applications. In IEEE Transactions on Antennas and Propagation; 2021;69(2):698–707.
12. Zhou Z, Wei Z, Tang Z, et al. Design and Analysis of a Wideband Multiple-Microstrip Dipole Antenna with High Isolation. IEEE Antennas and Wireless Propagation Letters. 2019;18(4):722–726.
13. Mustafa Khalid T. Combined Fractal Dipole Wire Antenna. 2007 2nd International ITG Conference on Antennas; Munich, Germany. 2007:176–180.
14. Yang Z, Jinghui Q, Tenigeer, et al. Design of a Novel Ultrawideband Wire Antenna With Enhanced Bandwidth. In IEEE Antennas and Wireless Propagation; 2012;11:624–627.
15. Hoch GR, Nayeri P, Elsherbeni A. Bandwidth enhancement of dipole antennas using parasitic elements. 2015 31st International Review of Progress in Applied Computational Electromagnetics (ACES); Williamsburg, VA, USA. 2015:1–2.