The functionalizing molecules (atoms) at a surface are considered for charge transfer between a molecule and substrate (CNT or graphenes). It is shown that at initial and intermediate stage of functionalization the intermolecular interaction can be described as electrostatic dipoles and quadrupoles ones. This model explains a homogeneous (sometimes periodic) distribution of adsorbed particles found in the experiments.

Keywords: adsorption, charge transfer, multi pole electrostatic interaction, graphenes, CNT Pacs 79.60.Dp

Carbon nanotubes (CNTs) are 1D nano materials, quantization along axis exists; CNT is considered as quantum wire or quantum dot.¹ Functionalization is powerful method for tuning CNTs quantum energy levels and physical properties. Functionalization of 2D graphene and bigraphene layers is also applied widely. The theory was developed² for energy spectra tuning in the semiconducting nanowires and polarons formation as the result of functionalization by molecular layers with (i) radial degree of freedom, (ii) conformational transition in the molecules and (iii) incommensurate structures. Periodic distribution of metals, metal organic³ and conducting polymers at CNT surface was found by TEM.⁴ The charge transfer³ leads to electron and hole (pair), spatially separated in neighboring substrate (CNT) and a molecule or atom. The aim of this work is theoretical consideration of initial stages of functionalization with the charge transfer. It is shown that the electron-hole pairs can be presented as the dipole and quadrupole moments with long range interaction. We consider situation of enough small molecules with relatively large distance between ones. At short range distances, compared with the molecules size, the proposed method would be applied with higher error. The charge transfer is example of a general contact interaction of molecules with different electro negativity. Thus, in comparison with CNT and graphene we have electronegative molecules with F, Cl, O, N. P, S atoms and electropositive metals or metal-organic complexes. In further consideration we suppose the molecules (atoms) to be electropositive and the electronic clouds of the transferred charge to be negative, they are shown in Figure 1. A dipole vector⁵ d = qr is shown as arrow between centers of negative and positive charges in Figure 1. Following to^5,6 we write dipole-dipole interaction as:

$U_{dd } = \frac{d^2}{R^3} [({\omega }_1{\omega }_2)-3({\omega }_{{}_1}n)({\omega }_{2}n)]$ ………(1)

where R is the radius-vector between centers of the dipoles 1 and 2,$R= \left|R\right|$ the unit vectors ${\omega }_{1 }$ ,${\omega }_{2 }$ and $n$  are directed along $d_{1 }$ $d_{2 }$ and $R$ Force between two particles for (1) is

$F_{ij } = - \frac{d{U}_{ij}(R)}{dR} = - \frac{1}{dR} [\frac{A}{R^K}] = \frac{K}{R} U_{ij}(R)$ …..(2)

where factor A is function of all parameters except distance R. In (1) power k = 3 and U_ij = U_dd. In next formulae k = 4; 5 and U_ij = U_Qd;U_QQ. Positive F means repulsion. The dipoles configuration in Figure 1 gives according (1, 2) F₁₂ > 0 and F₁₃ < 0 because of $({\omega }_{1}n)$ =0 and $({\omega }_1{\omega }_2)$ > 0 but $({\omega }_1{\omega }_3)$ < 0Increasing of the functionalizing molecules concentration leads to formation of different clusters^3,4 which can't be described in the present model. Only the small clusters with the multiple numbers N of the molecules can be described by (1) applying d_N = Nd₁. A renormalization of the charge transfer can arise depending on the cluster size (multiple numbers N). The nanobelts, nano spheres, nanocrystals are formed at CNT or nanowire surface^3,4 at higher concentration of the functionalizing molecules. These structures are periodic or almost periodic. The nanobelts are schematically depicted in Figure 2. We propose to describe the nanobelts with charge transfer as electric quadrupole. Definition of tensor of electric quadrupole moment is ${{\displaystyle Q}}_{ab}={\displaystyle \sum Q_a}{x}_a{x}_b$ (5). In the main axes and after normalization SpQ_aa = 0 the quadrupole moment in axe-symmetric case is described by only one parameter Q.^5,6 In Figure 2 external arrangement of the positive ions gives Q > 0. Dipole-quadruple U_Qd and quadruple-quadruple U_QQ interactions are:⁶

$U_{Qd } = - \frac{3Qd}{2R^4} [({\omega }_{1}n)+2({\omega }_1{\omega }_2) ({\omega }_{2}n)-5({\omega }_{1}n){({\omega }_{2}n)}^2]$ …….(3)

$U_{QQ } = - \frac{3Q^2}{4R_0{}^5} [1-5{({\omega }_{1}n)}^2-5{({\omega }_{2}n)}^2+2{({\omega }_1{\omega }_2)}^2+35{({\omega }_{1}n)}^2{({\omega }_{2}n)}^2-20({\omega }_{1}n)({\omega }_{2}n)({\omega }_1{\omega }_2)]$ …..(4)

Here Q is the nanobelts quadrupolar moment, R is the distance between centers of a quadrupole and a dipole or between two quadrupoles, n,${\omega }_1$ , ${\omega }_2$ are unit vectors. nǁR. In (3) ${\omega }_1$ ǁ $d_1$ In (4) ${\omega }_1$ ,${\omega }_2$ direction is along the quadrupole axes. For the dipole and quadrupole in Figure 2 ${\omega }_1$$\perp$${\omega }_3$ $A_{Qd }$ $\simeq +12Qd$ $({\omega }_3{n}_{31})$ and< 0,at large distances . According to (3,2) an indifferent equilibrium of the dipole between the nanobelts and weak attraction at short distances exist. Two nanobelts repulsion in Figure 2 is due to $A_{QQ }$ =6Q² >0 or F12 > 0 in (4,2). Another case of quadrupoles formation is intercalation into bigraphene or graphite, see Figure 3. Adsorption, functionalization and electrostatic multipolar interactions at CNT and graphene surfaces 3. It seems, to provide the charge transfer into two planes it be better to have higher valence of intercalating atoms. Values $({\omega }_{1}n)$ = 0

and A_QQ =(3=4)Q² in (4,2) means repulsing.

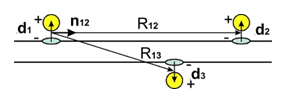
Figure 1 The adsorbed molecules or atoms (yellow spheres) at substrate (CNT, graphene) with transferred electrons (blue ellipses) gives repulsion of dipoles d1ǁǁd2. Opposite dipoles d1; d3 are attracted at semiconducting CNT or bi graphene.

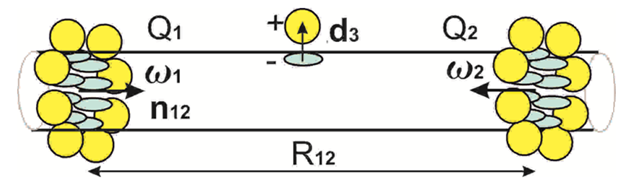
Figure 2 The quadrupoles Q1, Q2 formed by nanobelts of the adsorbed atoms at CNT sur-face are repulsed according (4). The intermediate dipole is unstable due to nanobelts attraction.

Figure 3 The quadrupoles formed by the inter-collated molecules are repulsed into bi graphene.

None.

The authors have no conflicts of interests in this work.

1. Dekker C. Carbon Nanotubes as Molecular Quantum Wires. Phys Today. 1999;52(5):22–28.
2. Victor A, Lykah, Eugene S Syrkin. Polarons in the functionalized nanowires. In: Laref A, editor. Recent progress and perspectives. New York: Nova Science Publishers.
3. Eder D. Carbon Nanotube-Inorganic Hybrids. Chem Rev. 2010;10(3):1348–1385.
4. Park SJ, Kwon OS, Lee JE, et al. Conducting Polymer-Based Nanohybrid ransducers: A Potential Route to High Sensitivity and Selectivity Sensors. Sensors. 2014;14(2):3604–3630.
5. Landau LD, Lifshits EM. The Classical Theory of Fields. Pergamon, New York. 1975:374.
6. Freiman Yu A, Manzhelii VG. Physics of Cryocrystals. New York: AIP-Press; 1997:691.