Foresters often don’t fully utilize available information when estimating average stand tons ac^–1. Previous experience, and if available historic inventory data, of the same tract or similar tracts can be used as prior information in a Bayesian context to reduce uncertainty associated with average ton estimates. Bayesian methods produce a posterior distribution dependent both on the current forest inventory sample and prior information about the probabilities associated with any one average tons ac^–1 actually being the true average tons. A more complete description and background of using Bayesian methods to incorporate personal knowledge, when estimating average tons, is provided. Additionally, a practical example using data obtained from an actual forest inventory conducted in a loblolly pine (Pinus taeda L.) plantation is presented. Using conventional variable plot sampling techniques, average tons was estimated at 52.9 tons ac^–1. However, when determining a posterior distribution using a Beta distribution to quantify prior personal knowledge of similar sites, the estimate of average tons changed to 51.6 tons ac^–1. When using a Uniform distribution to quantify prior knowledge the estimated average tons did not change. For this example, ton estimates were not substantially changed when using a Bayesian approach; however, the inferential statements that can be made about the true average tons are different than when using a frequentist inference approach.

Keywords: bayesian inference, frequentist inference, posterior distributions, uncertainty.

Foresters often don’t fully utilize available information when conducting forest inventories estimating average tons per acre, further referred to as average tons. For instance, beyond estimating a required sample size to obtain a certain level of precision, many foresters assume the only information available to them is the current sample estimate. However, when using Bayesian inference to account for uncertainty associated with an average ton estimate, foresters can incorporate personal knowledge about the true average tons into their estimate.

Traditionally, frequentist inference has been used to quantify uncertainty when estimating average tons. When using this approach, one assumes a parametric sampling distribution for a statistic based on an estimated mean and standard error of the mean obtained from a sample–in our case average tons estimated from a timber cruise.¹ For clarification, a sampling distribution is all possible values of a statistic for a given sample size and sampling protocol. A sampling distribution arises because we are estimating a parameter (e.g. true average tons) based on a sample and there is uncertainty associated with that estimate. In terms of average tons for a particular tract, when using 20 variable radius plots and a particular sampling scheme (e.g. random starting point followed by a systematic location of points), there is almost an infinite number of possible ways within the tract where the 20 points could be established. Each different positioning pattern of the 20 points would produce an estimate of average tons. A sampling distribution is the distribution of the estimates of all the different positioning patterns.

Probabilities associated with the uncertainty of an estimate are based on the theoretical concept of establishing repeated random samples of the same sample size using the same field methodology (e.g. systematically locating variable radius points). Each of the samples generates confidence intervals, so many are assumed to include the true average tons (or the parameter). Hence, when using a confidence coefficient of 95%, it is assumed that 95% of the confidence intervals will encompass the true average tons.^2,3 Notice the probability is on the confidence intervals, not the true average tons. The true average tons are a parameter and hence constant, it doesn’t change across repeated random sampling.⁴ However, what changes are the observational units (e.g. plots or points) contained in a particular sample and hence the generated confidence intervals.

Many applications of confidence intervals are interpreted incorrectly. Stating there is a 95% chance that the true average tons is contained within a single sample generated confidence interval the probability is incorrectly placed on the parameter, a fixed value that has no probability. However, Bayesian inference credible intervals do quantify the probability that the true average tons is contained within an interval.^2,3 If not always, then certainly often, this is what foresters are interested in McCarthy MA et al.³ They are not interested in determining the likelihood of confidence intervals generated from repeated random samples containing the true average tons. Bayesian inference combines ‘prior’ information about the likelihood of a particular average tons being the correct value and an estimate of average tons based on a sample to produce a posterior distribution.^2–4 The posterior distribution can be viewed as an updated set of probabilities about the average tons. It represents our state of knowledge about average tons in light of the data.

Additionally, Bayesian inference also addresses other issues with using frequentist inference to quantify uncertainty. As foresters, we know the assumption of a normally distributed (or t–distributed in practice) sampling distribution for estimates of average tons is often unrealistic. For example, in a stand consisting of at least one tree meeting limiting requirements, average tons cannot be negative or zero. However, confidence intervals developed based on frequentist inference can include negative or zero volume estimates.

Differences between bayesian inference and frequentist inference

Both Bayesian and frequentist inference attempt to quantify uncertainty about an estimate due to sampling error, but differ in their approach. McCarthy MA et al.³ for a more complete discussion about the differences between the two approaches.

Frequentist inference quantifies uncertainty based on conducting an infinite number of random samples from a population. For instance, a confidence coefficient is used to determine the probability that over repeated random sampling a percentage of the confidence intervals will encompass the true mean. In practice only one random sample is conducted but based on the Central Limit Theorem we can assume the sampling distribution of a mean is normally distributed. It should be made clear that the parameter, in our case true average tons, is not random across repeated random sampling–rather the confidence intervals are random.

Unlike frequentist inference, Bayesian inference allows for the parameter to be random and thus this approach can be used to determine the probability that the true mean is within some interval, referred to as credible intervals.^2,3 This is one of the major differences between these two approaches in regard to quantifying uncertainty. It should be clarified that Bayesian inference still assumes the parameter is fixed, or that there is a single, true average tons.³ However, it provides a means to assign probabilities to what the true average tons may equal.

Credible intervals are based on prior information updated using one sample while confidence intervals are based on expected behavior across repeated random sampling using results from one sample. Hence, Bayesian inference provides probabilities for parameters, given the data, in contrast to the logic of frequentist inference, which provides probabilities for datasets, given the parameter.⁴ A second major difference is that two–sided confidence intervals based on the Central Limit Theorem, by definition, are symmetric about the estimated average tons while credible intervals are not absolutely symmetrical.

A third major difference between the two approaches is that Bayesian inference allows a forester’s prior knowledge, or prior information, to be incorporated when quantifying uncertainty. Bayesian inference through the use of prior information alters the estimated sampling distribution (estimated based on the Central Limit Theorem) of an average ton estimate obtained from a current forest inventory. As an example of prior information about an estimate of average tons, consider a forester who has been told by a private landowner that a particular stand of timber is an unthinned, undamaged, 25–year old loblolly pine (Pinus taeda L.) stand planted at a density of 450 seedlings ac^–1. Based on previous experience, that forester will have a good idea of the average tons prior to visiting the stand. With additional information such as site preparation, herbicide and fertilization treatments, and site index, the forester is likely to have an even better idea of the average tons. Surely, the true average tons cannot be 0, nor is it likely to be 10 tons ac^–1, or even 30 tons ac^–1, and thus these average tons should not be considered to occur within the sampling distribution.

As a second example of prior information, assume a forester conducted a forest inventory 5 years ago on a tract to be reinventoried for management purposes. Based on experience and previous inventory data, that forester can estimate a reasonable range of the current average tons and the most probable average tons prior to sampling the tract. In both cases, the forester’s ‘prior’ information can be used to alter the estimated sampling distribution of average tons that would otherwise be exclusively based on the current sample. This altering of the sampling distribution does not require any additional field work, only experience and/or previous data. When incorporating prior information about the estimated average tons, we have reduced the uncertainty associated with that estimate prior to conducting the forest inventory.

Bayesian inference raises the question, since we never really know the true average tons, and a sample is conducted only once for a particular inventory of a tract, what is to say the sample estimate is exclusively representative of the true average tons. For instance,¹ state in some cases the confidence interval constructed under a frequentist inference approach will not include the true average tons. In these cases, Bayesian methods can be particularly helpful to ensure that a reasonable estimate of the true average tons is obtained. Although there is considerable debate about which inference approach is correct, some statisticians recognize the utility of both approaches.²

Incorporating prior information

Incorporating prior information is accomplished by using a distribution quantifying probabilities associated with average tons actually being the true average tons prior to sampling,. Two commonly used distributions in other natural resource Bayesian applications are the Uniform and Beta.^5–7 When using the Uniform distribution to describe prior information, a range of values is assumed to be equally likely. Thus, the forester only has an idea of the range of likely tons. As for the Beta distribution, a forester not only has an idea of the range of likely tons but is confident that within the range, certain tons are more likely to be the true average tons. Thus, when using a uniformly distributed prior, a forester needs to quantify the expected minimum and maximum average tons prior to sampling. In addition, and if confident, a forester can specify the most probable average tons allowing for the use of a Beta distributed prior. Though a normal distribution can also be used to quantify prior probabilities, a Beta distribution, in my opinion and for our use, is preferable to the Normal distribution as a prior because the Beta has true minimum and maximum limits and can assume a variety of shapes.

In Bayesian analyses, the prior distribution is used along with the sample estimated sampling distribution (Likelihood) to obtain a posterior distribution. The posterior distribution is equivalent to describing the uncertainty associated with an estimate of average tons conditional on the current sample and the prior information. Generally, the estimated average tons based on Bayesian methods will be different from the forest inventory sample estimate due to the impacts of the priors.

Bayesian methods have been used in many natural resource applications.^6–8 However, there is limited published literature that addresses the use of Bayesian methods when conducting a forest inventory to estimate average tons within a given stand of timber. Therefore, the objectives of this paper are to (i) explain some of the differences between frequentist and Bayesian inference when estimating average tons, (ii) describe the process behind using Bayesian methodology to estimate average tons, and (iii) provide an example from an actual forest inventory to estimate average tons.

Determining posterior probability distributions
Equation (1) expresses how posterior probability distributions are calculated based on the sample data and the priors:⁹

$P\left\{To{n}_i\right|data\}=\frac{L\left\{data\right|To{n}_i\left\}P\right\{To{n}_i\}}{{\displaystyle \sum _{i=1}^n[L\{data\left|To{n}_i\right\}P\left\{To{n}_i\right\}}]}$                                      (1)

Where:
$P\left\{To{n}_i\right|data\}$ – is the posterior probability associated with any average ton ($To{n}_i$ ) being the true average tons based on the sample and the prior information (a strict probability between 0 and 1). For those tons outside the range of the prior minimum and maximum average tons, the probability will be 0, $L\left\{data\right|To{n}_i\}$ –is the probability of observing the sample data given a particular average tons ($To{n}_i$ ) is the true average tons. This is the same probability as the Likelihood of observing the data given a particular ton is the true average tons. In practice, this probability is calculated based on using a t distribution centered about the sample estimated average tons with dispersion based on the estimated standard error of the mean, the traditionally used procedure to quantify uncertainty when conducting a forest inventory, and ${\displaystyle \sum _{i=1}^n[L\{data\left|To{n}_i\right\}P\left\{To{n}_i\right\}}]$ – is the summation of all joint probabilities of $L\left\{data\right|To{n}_i\}$ and$P\left\{To{n}_i\right\}$ . In practice, we do not need to directly calculate the sum. We can obtain this value in a sense by multiplying $P\left\{To{n}_i\right\}$ and $L\left\{data\right|To{n}_i\}$  for some step interval of$To{n}_i$ , summing up the probabilities associated with all $To{n}_i$  based on the step interval, and then dividing a particular $To{n}_i$  probability by that sum. An example is provided to make this procedure clearer (Table 1 & 2).

Determining prior probability distributions–$P\left\{To{n}_i\right\}$
For this paper, we use two distributions to quantify probabilities associated with a particular average tons being the true average tons prior to inventorying the stand. One is the Uniform (equation (2)) and the second is the Beta (equation (3)):

$f\left(y\right)=\frac{1}{\text{Max}-\text{Min}}; \text{Min}\le y\le \text{Max}$                                (2)

$f\left(y\right)=\frac{(\text{α}+\text{β-1)!}}{(\text{α-1)!}(\text{β-1)!}}\frac{{(y\text{ - Min)}}^{\text{α-1}}{(\text{Max-}y\text{)}}^{\text{β-1}}}{{\text{(Max-Min)}}^{\text{α}+\text{β-1}}}; \text{Min}\le y\le \text{Max}$        (3)

Where:
y–any average tons ($To{n}_i$ ) within the range of the specified minimum (Min) and maximum (Max) values prior to sampling, including the minimum and maximum values themselves, Min, Max– are the estimated minimum and maximum average tons prior to sampling; respectively, and $\text{α, β}$ – are parameters to be estimated.

In practice, a simplified version of equation (3) can be used to obtain probabilities proportional to the Beta probabilities:

$f\left(y\right)={(y\text{ - Min)}}^{\text{α-1}}{(\text{Max-}y\text{)}}^{\text{β-1}}; \text{Min}\le y\le \text{Max}$                                (4)

As mentioned in Van Oijen et al.⁶ care should be taken to avoid being excessively precise in determining the prior probabilities of average tons. To clarify, for example, we mean defining too narrow of a range of the minimum and maximum average tons beyond what is reasonable prior to conducting a forest inventory. When using Bayesian inference, the range of the priors will be the range of the posterior distribution. An unreasonably narrow range of the priors will severely limit the impact of the data on the posterior distribution.

Obtaining a Bayesian estimate of average tons using actual forest inventory data
Study area description
The study area was located in a 40–acre thinned loblolly pine plantation around five miles southwest of Monticello, Arkansas (33.6290° N, 91.7910° W). This site was row–thinned and was nearly pure loblolly pine (Figure 1). The soil is mainly classified as coarse–silty, siliceous, active, thermic Glossaquic Fragiudults and fine–silty, siliceous, semi active, thermic Typic Endoaquults. Site index is around 90 ft (base age 50). A total of twenty 20–BAF (Basal Area Factor) points (English units) were established using a prism. Trees ac^–1, total average basal area ac^–1, and total average tons ac^–1 were estimated to be 175, 79 sq ft, and 52.9, respectively. Tons ac^–1 had a standard deviation of 18.71 and a standard error of the mean of 4.18. Quadratic mean diameter was 9.1 in.

Figure 1 Location map and aerial photograph of the loblolly pine plantation used to conduct the inventory. The study area was located in a 40–acre thinned plantation around five miles southwest of Monticello, Arkansas (33.6290° N, 91.7910° W).

Forest Inventory sample procedures
In the summer of 2008, a total of 79 trees were sampled across 20 variable radius points. The points were established using a systematic grid to ensure distribution across the site. A 20 ft² ac^–1 BAF was selected based on the “rule of thumb” of 4–8 trees per sampling point. Only live loblolly pine trees $\ge$ 4 in. were measured and recorded for analysis. Equations presented in Bullock BP et al.¹⁰ were used to estimate tons.

Prior distributions
Based on previous experience and prior to conducting the inventory, reasonable minimum and maximum average tons of 32 ac^–1 and 66 ac^–1 were determined; respectively. For the uniform distribution, all volumes within the range of 32–66, including 32 and 66, are equally likely to occur. In order to use the Beta distribution, the most probable average tons of 47 ac^–1 was determined. To obtain estimates of $\alpha$  and $\beta$  for the Beta distribution, a PERT analysis technique¹¹ was used to first estimate the mean,$\overline{\text{V}}$  and variance,${\text{S}}_{\text{V}}^{\text{2}}$  of the Beta distribution based on the minimum, maximum, and most probable average tons:

$\overline{\text{V}}=\frac{\text{Min }+{\text{ 4V}}_{\text{p}}+\text{Max}}{6}$                                         (5)

$t=\frac{\left(y-52.9\right)}{4.18}$                                                       (6)

Where:
Min–minimum expected average tons prior to sampling,${\text{V}}_{\text{p}}$ –most probable average tons prior to sampling, and
Max–maximum expected average tons prior to sampling.

Thus, estimates of $\overline{\text{V}}$ and ${\text{S}}_{\text{V}}^{\text{2}}$  for our data are:

$\overline{\text{V}}=\frac{32+4(47)+66}{6}=47.67$

${\text{S}}_{\text{V}}^{\text{2}}=\frac{{(66-32)}^2}{36}=32.11$

The parameters $\alpha$  and $\beta$  that describe the shape of the Beta distribution were then estimated:

$\alpha =\left[\frac{\overline{\text{V}}\text{- Min}}{\text{Max - Min}}\right]\left[\frac{(\text{Max-}\overline{\text{V}})(\overline{\text{V}}-\text{Min)}}{{\text{S}}_{\text{V}}^{\text{2}}}-1\right]$                                        (7)

$\beta =\alpha \left[\frac{\text{Max -}\overline{\text{V}}}{\overline{\text{V}}\text{- Min}}\right]$                                                                   (8)

For our data, estimates of the parameters are:

$\alpha =\left[\frac{47.67-32}{66-32}\right]\left[\frac{(66-47.67)(47.67-32)}{32.11}-1\right]=3.66$

$\beta =3.66\left[\frac{66-47.67}{47.67-32}\right]=4.28$

To obtain probabilities associated with any average tons proportional to the Beta probabilities, estimated Min and Max values and parameters were placed into equation (4):

$f\left(y\right)={\left(y-32\right)}^{3.66-1}{\left(66-y\right)}^{4.28-1}$

Determining the likelihood of the observed data–$L\left\{data\right|To{n}_i\}$
Based on the estimated average tons and standard error from the actual timber cruise, a t distribution was used to describe the probability (Likelihood) of observing the data given a particular $To{n}_i$  is the true average tons. Despite the Bayesian inference complex terminology, this is nothing more than the usual practice of describing uncertainty associated with the estimated average tons from a forest inventory. A t–score is calculated as:

$t=\frac{\left(y-\overline{y}\right)}{{\text{s}}_{\overline{y}}}; \text{-}\infty \le y\le +\infty$                                                     (9)

Where:
$y$ –Average tons,
$\overline{y}$ –Estimated average tons from the forest inventory, and ${\text{s}}_{\overline{y}}$ –Standard error of the mean.

Thus, based on results from the forest inventory, equation (9) becomes:

$t=\frac{\left(y-52.9\right)}{4.18}$

For this analysis, probabilities of the t–score were generated using procedures in Microsoft® Excel (tdist[t, 19, 2]/2).

Estimating posterior distributions $P\left\{To{n}_i\right|data\}$
The posterior distribution was obtained by multiplying the probability of observing the sample data given a particular tons is the true average tons, $L\left\{data\right|To{n}_i\}$ , and the prior probability associated with any one particular average tons being the true average tons prior to sampling based on either the Uniform or Beta distributions. After manipulating the posterior distribution to integrate (or sum in practice) to unity as mentioned in the Determining posterior probability distributions section, by calculating the expected value of the posterior distribution an estimate of the average tons was obtained:

$E[\{To{n}_i\left|data\right\}={\displaystyle \underset{\text{Min}}{\overset{\text{Max}}{\int }}To{n}_{i}f\left(y\right)dy}$                                       (10)

In practice, an estimate of this integral is obtained from:                                                                           

$E[\{To{n}_i\left|data\right\}]={\displaystyle \sum _{\text{Min}}^{\text{Max}}To{n}_{i}f\left(y\right) }$  (11)
Where:
Min and Max–minimum and maximum average tons as specified by the prior distribution; respectively, and
f(y)–are probabilities obtained from the posterior distribution, $P\left\{To{n}_i\right|data\}$ .

When using equation (11), smaller step intervals (e.g. 32.1, 32.2, 35.3 … as opposed to 32, 33, 34…) will likely provide a closer approximation to the true integrated value shown in equation (10) because we are using a discrete approach to quantify continuous distributions (e.g. Beta, Uniform, and t).⁹ A lower credible interval for the estimate of average tons can be obtained by summing the posterior probabilities to some level of confidence (e.g. 0.025 for a two–sided 95% credible interval). An upper credible interval can be obtained in a similar manner (e.g. 0.975 for a two–sided 95% credible interval). Although more advanced integration techniques exist, this simple discrete approach can be implemented fairly easily within Microsoft® Excel.

When using prior information to estimate tons along with the forest inventory sample, the estimated average tons didn’t change based on a Uniform prior distribution but it changed from 52.9 tons ac^–1 to 51.6 tons ac^–1 (–1.3 tons) when using a Beta prior distribution (Table 1 & 2). Differences in the posterior estimate of average tons arise because of varying strengths of the priors.^4,9 Compared to the Beta prior distribution, the Uniform prior distribution is relatively weak in its influence and the data had a greater impact on the posterior distribution.

Although confident in the forest inventory protocol, due to random sampling error, the conventional point–sampling estimate most likely does not equal the true average tons. Based on previous experience, I was relatively confident that the true average tons ranged from 32 tons ac^–1 to 66 tons ac^–1, and thus Bayesian methods adjusted the estimated sampling distribution (quantified using a t–statistic) such that all tons outside this range had zero probability. All probabilities of tons outside the range of 32 tons ac^–1 and 66 tons ac^–1 when using the t–distribution have been “pushed” inwards² producing taller but narrower posterior distributions (Figure 2) (Figure 3). This arises because before even conducting the timber cruise, the uncertainty associated with the estimate of average tons was decreased because of the prior information.³ For the Beta prior distribution, the posterior distribution is more definitively non–symmetric. Approximate 95% credible limits are in bold text in Tables 1 & 2.^2,3 A smaller step interval would likely produce more precise estimates of the limits. Values of the 95% confidence limits using a frequentist inference approach are 44.2 tons ac^–1 and 61.6 tons ac^–1.

Figure 2 Posterior distribution of average tons ac^–1 (bold line) based on a uniformly distributed prior and sample data obtained from a loblolly pine plantation in southeastern Arkansas. The lighter line is the estimated sampling distribution based exclusively on the forest inventory sample and the t–distribution.

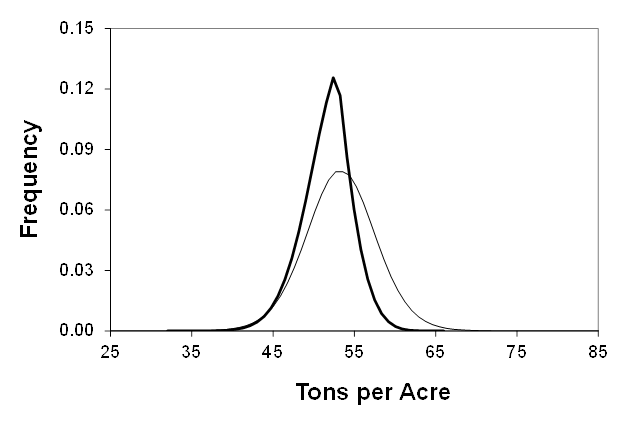
Figure 3 Posterior distribution of average tons ac^–1 (bold line) based on a Beta distributed prior and sample data obtained from a loblolly pine plantation in southeastern Arkansas. The lighter line is the estimated sampling distribution based exclusively on the forest inventory sample and the t–distribution. Notice the posterior distribution is non–symmetric due to the strength of the Beta distributed prior to alter the normally distributed likelihood distribution.

Although ton estimates do not differ much after incorporating ‘prior’ information, the inferential statements that can be made vary substantially. Rather than stating that we are 95% confident that an interval about the sample mean encompasses the true average tons, we can calculate probabilities about the value of the average tons using credible intervals.^2,3 Additionally, the credible intervals do not need to be symmetrical since they are not calculated based on the assumption that sample means are normally distributed about the population mean. Finally, I have incorporated personal knowledge when calculating the uncertainty associated with the estimate of average tons.

As the standard error of the mean decreases and sample size remains constant, the observed data will have a greater impact on the posterior distribution.⁴ This is not surprising since we are using Bayesian methods in part to account for sampling error, as sampling error decreases the impacts of the prior information should be less. If the standard error of the mean remains constant, increases in sample size will also result in the observed data having a greater impact on the posterior distribution resulting from a narrower t–distribution.

A few comments about prior distributions should be made. It is true that a ‘Bayesian’ bears responsibility for the appropriate selection of priors.⁴ In Bayesian inference, the posterior mean is a weighted function of the prior mean and the sample mean where the weights are the relative levels of precision.^2–4 Priors influence posteriors, particularly with small–sample datasets. A so–called non–informative prior can be selected. A non–informative prior is one that has such a large variance that it will have little or no impact on the posterior distribution.^2,3 In fact, when one has incorrectly interpreted a frequentist inference to mean that there is some probability that the true average tons is within an interval, actually the interpretation would have been correct if using Bayesian inference and an assumption of a true non–informative prior.³ Therefore, most forester’s interpretation of quantifying the uncertainty associated with an average tons estimate has not been incorrect, they have just not known they were using Bayesian inference (and an assumption of a true non–informative prior).

As to the timing of when exactly a forester specifies their ‘priors’ is a matter of preference. For instance, if a forester knows for a particular plantation the planting density, age, site index, number of thinning, and has viewed aerial photographs, they can specify a very knowledgeable lower and upper bound. Almost all industrial land and much non–industrial land have these records. However, it would also be legitimate to use not only that information, but let us say a forester visits the stand before specifying their ‘priors’. This is also legitimate, obviously the forester would have a much better idea of the actual stocking of the forest and could incorporate this knowledge when specifying their ‘priors’.

An application of using Bayesian methods to incorporate prior personal knowledge when conducting a forest inventory for average tons estimates was presented. Bayesian analyses incorporate prior information about a parameter along with sample data to produce a posterior distribution. Before conducting a forest inventory, prior information may help reduce uncertainty associated with an estimate of average tons. Based on a forester’s previous experience, the posterior distribution should be more representative of what tons are actually expected to occur for a particular forested tract relative to conventional confidence intervals. Methodology presented in this paper can be applied to many forest types and for any desired measure of yield (e.g. tons, volume, biomass, carbon). Additionally, this methodology can be used to produce posterior distributions of other critical stand variables including basal area ac^–1 and trees ac^–1.

None.

Author declares there is no conflict of interest.

1. Avery TE, Burkhart HE. Forest Measurements. 5th ed. USA: McGraw–Hill; 2002. 456 p.
2. Casella G, Berger RL. Statistical Inference. 2nd ed. USA: Duxbury, Pacific Grove; 2002. 660 p.
3. McCarthy MA. Bayesian methods for ecology. UK: Cambridge University Press; 2007. 296 p.
4. Stauffer HB. Contemporary Bayesian and Frequentist Statistical Research Methods for Natural Resource Scientists. USA: John Wiley & Sons; 2008. 400 p.
5. Green EJ, MacFarlane DW, Valentine HT, et al. Assessing uncertainty in a stand growth model by Bayesian synthesis. Forest Science. 1999;45(4):528–538.
6. Van Oijen M, Rougier J, Smith R. Bayesian calibration of process–based forest models: bridging the gap between models and data. Tree Physiology. 2005;25(7):915–927.
7. Bullock BP, Boone EL. Deriving tree diameter distributions using Bayesian model averaging. Forest Ecology and Management. 2007;242(2–3):127–132.
8. Clough BJ, Green EJ. Comparing statistical approaches for selecting optimal models of stem volume in loblolly pine plantations. Forest Science. 2016;62(1):9–17.
9. Haddon M. Modelling and quantitative methods in fisheries. USA: CRC Press; 2001. 406 p.
10. Bullock BP, Burkhart HE.  Equations for predicting green weight of loblolly pine trees in the South. Southern Journal of Applied Forestry. 2003;27(3):153–159.
11. Farnum NR, Stanton LW. Some results concerning the estimation of beta distribution parameters in PERT. Journal of the Operational Research Society. 1987;38(3):287–290.