The laws of physics, namely the gas laws, were applied to the gases in the atmosphere that act as ideal gases. The results show that as air temperature increases from winter to summer CO₂ is a cooling gas and from summer to winter it is a warming gas regardless of its concentration in the atmosphere. This is contrary to the commonly held belief that CO₂ always warms the atmosphere. Back radiation is the sum of the radiation of all of the greenhouse gases back to the Earth. It is a measured value and increases with temperature and vice versa. Back radiation acts opposite to that of CO₂, methane and the trace gases. On average, the latter account for 1.2% of back radiation and water vapor accounts for 98.8%. The effect of CO₂, methane and the trace gases on atmospheric temperature and climate change is so small as to be negligible.

Keywords: carbon dioxide, water vapor, back radiation, atmospheric temperature, climate change, radiative forcing

Current government policies are designed to reduce the consumption of fossil fuels because of the widespread belief that increasing levels of carbon dioxide (CO₂) in the atmosphere will cause large and dangerous warming of the Earth’s atmosphere. Because 80% of the world’s energy comes from coal, oil and natural gas and are vital to providing the food, clothing and shelter that are the cornerstone of the well–being of our people, it is imperative that we examine the validity of this widespread belief.

The concept that carbon dioxide (CO₂) is causing climate change comes from the fact that the concentration of CO₂ is increasing in the atmosphere from the burning of fossil fuels. This has increased the warming effect of CO₂ by approximately 1.7 Watts per square metre (Wm^–2) since 1750.¹ This is the basis for the belief that CO₂ is increasing atmospheric temperature. This belief is reinforced by the IPCC. They suggest that doubling of CO₂ concentration in the atmosphere from 280 ppmv in 1750 to 560 ppmv is expected to increase the atmospheric temperature by a dangerously high 3°C.

A key argument against CO₂ as the cause of climate change uses the laws of physics, namely the gas laws, and the measured value of back radiation to show the effect of CO₂ on atmospheric temperature. The gas laws applied to the gases in the atmosphere show CO₂ is a warming or a cooling gas depending on the time of year regardless of its concentration. Radiation warming from CO₂ is a small part of back radiation, which is the total radiation back to the Earth from all of the greenhouse gases. As shown in Figure 1, the portion of back radiation by CO₂ is very small compared to the total, approximately 0.6%. Virtually all of back radiation comes from water vapour and it acts opposite to that of CO₂. Thus, while CO₂ is trying to warm the atmosphere, water vapor is cooling it and vice versa.

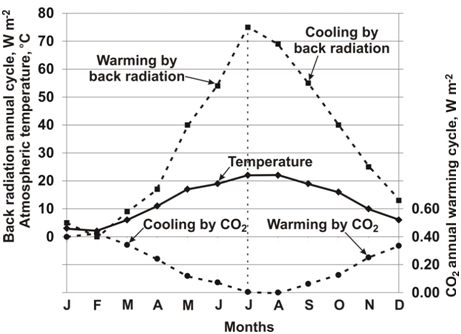
Figure 1 The warming effect of back radiation rises by 70Wm^–2 from January to July while CO₂ causes cooling of 0.45 Wm^–2as its concentration falls.

The purpose of this paper is to provide the details for constructing Figure 1 and to provide the evidence that the warming effect of CO₂ on the atmosphere is small enough to be negligible. This paper builds on the statement in Lightfoot et al.,² “back radiation acts in opposition to the warming effect of the CO₂” and provides new information. It provides the details necessary for the construction of Figure 1 that involve several scientific disciplines, such as, temperature and relative humidity records for Hamburg, Germany; the gas laws of Boyle and Charles/Gay–Lussac; psychrometric charts or programs; the back radiation measured at Hamburg; the concentration of CO₂ measured at Mauna Loa and the relative warming effect of various greenhouse gases (GHG) from Figure SPM.5.¹

The construction of Figure 1 leads to the evidence that all of the greenhouse gases can warm or cool the atmosphere depending on the conditions. Finally, evidence is provided showing the total warming or cooling effect of all of the ideal greenhouse gases, i.e., CO₂, methane and the trace gases, is approximately 1.2% of that of water vapor.

The starting point of this paper is an explanation of the baseline concentration of CO₂ as reported by the Mauna Loa Observatory. This baseline allows the calculation of the concentration of CO₂ at any time or place on Earth using the gas laws.

It is known that the concentration of water vapour as a GHG at any location can change over relatively short time periods and can be affected by atmospheric temperature. Similarly, the concentration of CO₂ and its warming effect can change depending on the elevation of the location and atmospheric temperature. In this paper, we show how to calculate the concentration of CO₂ at any location on Earth where the elevation and temperature are known and including dilution by water vapor.

Carbon dioxide acts as an ideal gas under the conditions of temperature and pressure experienced on Earth and obeys the gas laws, i.e., the physical laws relating pressure, temperature and volume of a gas that were discovered by Boyle and Charles/Gay–Lussac. Significant differences in elevations, atmospheric temperature and relative humidity (RH) are the cause of significant differences in CO₂ concentration around the Earth. These differences make it difficult to determine whether or not the average CO₂ concentration is increasing or decreasing. Thus, it is necessary to establish a system of measurement that eliminates the effect of pressure, atmospheric temperature and RH variations on CO₂ concentration and to establish a consistent baseline.

To develop a baseline, in 1959 Charles Keeling started measuring the mole fraction of CO₂ in dry air in parts per million molecules of dry air^3,4 at Mauna Loa and reported the results as parts per million by volume (ppmv) of dry air. The same measurements that Keeling started are continued today.⁵ There is some confusion about the number that is reported daily by the Mauna Loa Observatory. From the start of measurements in 1959 through the IPCC First⁶ and Third⁷ Assessment Reports the number was always reported as ppmv. Beginning with the IPCC Fourth Assessment Report,⁸ the number was defined as parts per million molecules of dry air (ppm). This definition is related to the composition of the atmosphere and composition does not change with pressure or temperature. It is also used to estimate the dilution of CO₂ by water vapor. However, it says nothing about the concentration that determines the warming effect of CO₂. Conveniently, the difference between the two values is very small, i.e., the ppmv value is approximately 0.3ppm lower than the ppm value at CO₂ concentration of 400 ppm.⁹ Because the difference is very small, approximately 0.075%, the same value is useful for each definition, ppm and ppmv, with negligible error.

For the ppmv definition, the baseline conditions are the well–known Standard Temperature and Pressure (STP, 0 °C and atmospheric pressure, 101325 Pascals) in dry air. This is consistent with the practice of measuring all of the calibration gases at STP¹⁰ at the Mauna Loa Observatory to ensure the accuracy of the CO₂ measurements. This STP baseline and the gas laws provide a means of calculating the CO₂ concentration at any location on Earth where the temperature, RH and elevation (The Engineering Toolbox)¹¹ are known. It is CO₂ concentration that determines the actual warming, or greenhouse effect, of CO₂ on the atmosphere, i.e., the number of CO₂ molecules per cubic metre or ppmv. The difference in warming effect, or radiative forcing (RF), of CO₂ between two concentrations is defined by the approximate logarithmic expressions developed in the TAR,¹ such as the simplified ΔRF = αln(C/C_o). The suggested value of α is 5.35. In AR4, the IPCC appears to have used a constant of 5.22 instead of 5.35 to calculate the difference between 275 and 378 ppmv as 1.66 Wm^–2 in Figure SPM.2.⁸ The constant of 5.22 is used in this study.

The U.S. Department of Commerce, National Oceanic & Atmospheric Administration, NOAA Research website titled: How we measure background CO₂ levels on Mauna Loa¹² gives the composition of the atmosphere when the portion of CO₂ is 372 ppm, and explains how to calculate the dilution of CO₂ by water vapor in the following paragraph and Table 1:

“For example, 372 parts per million of CO₂ (abbreviated as ppm) means that in every million molecules of (dry) air there are on average 372 CO₂ molecules. The table below gives an example for 372 ppm CO₂ in dry air. All species have been expressed as ppm, turning 78.09% nitrogen into 780,900 ppm. The rightmost column shows the composition of the same air after 3% water vapor has been added.” Using the method of Column C, at the current CO₂ concentration level of approximately 400 ppmv, the dilution by 30,000 ppmv of water vapor, 3%, is 12 ppmv. Because of rounding, columns B and C in Table 1 actually add to 999,999.

Parts 1 and 2 of Table 2 are an example of a spreadsheet table constructed to calculate the concentration of CO₂ at Hamburg, Germany as in columns J and K of Part 2. The procedure can be readily followed by reading the cell titles in alphabetical order. Table 2 can be adapted to calculate the concentration of CO₂ at any place on Earth.

Column I of Part 2 is the baseline CO₂ concentration of 407.9 ppmv issued on May 9, 2016 by the National Oceanic and Atmospheric Administration (NOAA) expressed as ppmv at STP. This value is above the average value for 2016 of approximately 404 ppmv. From the 407.9 baseline, the average July 1, concentration of CO₂ of 377.1 ppmv in dry air is calculated using the gas laws to adjust for pressure (elevation) and temperature (degrees, K) as in Equation 1:

July 1 CO₂ concentration = 407.9 x (101230/101325) x (273/295) = 377.1 ppmv in dry air (1)

The method of Column C in Table 1 is used to calculate 371.3 ppmv of CO₂ after dilution by 15,540 ppmv of water vapour, Column H.

Similarly, the January concentration of CO₂ is calculated as in Equation 2:

January 1 CO₂ concentration = 407.9 x (101230/101325) x (273/276) = 403.1 ppmv in dry air (2)

Regardless of the concentration of CO₂ in the atmosphere, the gas laws always show a decrease in concentration with increased temperature and vice versa.

Note that Column F in Part 1 requires the MegaWatSoft psychrometrics program (MegaWatSoft)¹³ to be installed behind an Excel spreadsheet. The same result can be obtained using physical psychrometric charts available from the American Society of Heating, Refrigerating and Air–Conditioning Engineers, Inc. (ASHRAE).¹⁴

The values in Column H are calculated from Column F for July as follows:

(0.009610 x 1,000,000) = 9610 ppm x (28.9645/18.016) = 15,450 ppmv (3)

where 28.9645 is the molecular weight of air and 18.016 is the molecular weight of water vapor.

The ratio of the number of water molecules to the number of CO₂ molecules in Column L is calculated using the baseline concentration of 407.9 ppmv. The ratio of the number of molecules is proportional to the concentration in parts per million by volume, ppmv. It is shown to help the reader better visualize the large differences in concentrations and warming effects between water vapor and CO₂.

A table similar to that of Table 2 was used to construct Figure 2, which is a monthly plot of the sun angle, average atmospheric temperature at Hamburg, CO₂ concentration in dry air and water vapor concentration (H₂O/CO₂ ratio) on the same graph. The H₂O/CO₂ ratio is the ratio of the number of water molecules to CO₂ molecules.

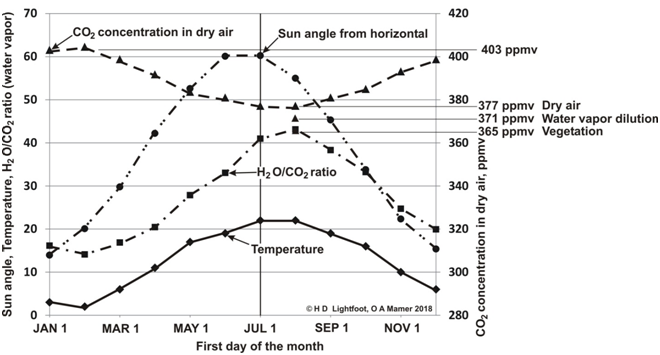
Figure 2 Seasonal record of sun angle, atmospheric temperature, CO₂ concentration in dry air and water vapor concentration (H₂O/CO₂ ratio) for Hamburg, Germany.

In Figure 2, it is the gas laws that cause CO₂ concentration in dry air to fall by 26 ppmv from 403 to 377 ppmv from January to August. As the air warms it expands and there are fewer molecules of CO₂ per cubic metre. Water vapor dilution causes CO₂ concentration to drop another 6 ppmv and the effect of vegetation in the Northern Hemisphere drops it another 6 ppmv to 365 ppmv. Over the same time period, the temperature rises from 3°C to 22°C. This is clear evidence that increased atmospheric temperature is associated with reduced CO₂ concentration.

In contrast to CO₂ concentration, actual weather records show water vapor concentration, the H₂O/CO₂ ratio, moves in synchronization with atmospheric temperature. For example, Table 2, Parts 1 and 2, show from January 1 to July 1 at Hamburg the temperature rises 19°C (Col. B), CO₂ concentration falls 26 ppmv (Col. J), water vapour rises by 9033 ppmv (Col. H), and the H₂O/CO₂ ratio raises 25.4 units (Col. L).

This is conclusive evidence that from winter to summer the warming by water vapor counteracts the small cooling by CO₂. Conversely, from summer to winter, the warming effect of CO₂ tends to warm the air as water vapor is cooling it. But the effects by CO₂ each time are so small as to be negligible. This evidence comes to light because the gas laws show that in the atmosphere CO₂ concentration falls as temperature rises. By examining the warming curves for water vapor² and CO₂ Lightfoot et al.,¹⁵ versus increased concentration separately from the atmosphere it appears logical to assume they are additive. Climate models consistently project increased atmospheric warming with increased CO₂ concentration in the atmosphere. This could not happen if the models accounted for the fact that the large warming and cooling effects of water vapor counteract the small cooling and warming effects of CO₂.

The inverse relationship between CO₂ and temperature also occurs daily as shown in Figure 3 for Montreal, Canada. For example on an average July 1 increasing temperature from 17 to 24°C towards the afternoon decreases the CO₂ concentration from 383.7 to 374.7 ppmv, a difference of 9 ppmv. Similarly to Figure 2, the plot of daily records also shows the H₂O/CO₂ ratio moves in the same direction as the temperature.

Figure 3 Average July 1 Montreal temperature, CO₂ concentration and H₂O/CO₂ ratio.

Figure 1 shows the measured difference in back radiation between January and July at Hamburg on the left hand axis as it increases from 298 to 368 Watts per square metre (Wm^–2). Over the same time period, the right hand axis shows the ΔRF of CO₂ calculated by ΔRF = 5.22ln(C/C_o) falls by 0.40 Wm^–2, or 0.6% of that of back radiation. The key point is that from winter to summer the warming by back radiation works against the small cooling effect of CO₂ when the two are together in the atmosphere. Similarly, from summer to winter, the cooling effect of water vapor works against the small warming effect of CO₂.

Table 3 summarizes the results of applying the calculations of Table 2 to the average weather records at four locations from the Arctic to the Tropics. These locations with latitude and elevation are Barrow, Alaska (71.32^oN, 3m), Hamburg (53.57^oN, 8m), Boulder, Colorado (40.05^oN, 1655m) and Kwajalein (8.71^oN, 3m).

The difference in back radiation on the average January 1 between the Tropics, Kwajalein, and the Arctic, Barrow, is (411–185) = 226Wm^–2 and on the average July 1 it is (421‒308) = 113Wm^–2. The summer is warmer than the winter because the average back radiation in summer is 360.5Wm^–2 versus 283.5 Wm^–2 in winter, Lines 5 and 6 of Table 3.

In comparison, the difference in warming by CO₂ on the average January 1 between the Tropics and the Arctic acts opposite to back radiation and is ΔRF = 5.22ln(444.8/358.1) = 1.13Wm^–2 and on the average July 1 ΔRF = 5.22ln(397.4/357.6) = 0.55Wm^–2. In other words, CO₂ reduces the January difference of 226 Wm^–2 by 1.13 Wm^–2, and the July difference by 0.55 Wm^–2.

From the Arctic to the Tropics, the warming effect of CO₂ is so small at 0.02% to 0.57% of that of back radiation that it has no significant effect on its magnitude.

Figure 4 is the average monthly back radiation in Wm^–2 recorded at Hamburg, Germany.¹⁶ Back radiation (BR) is a measured value and is the sum of the warming heat radiated back to the Earth by water vapor (WV), CO₂, and methane plus the trace gases as in Equation (4).

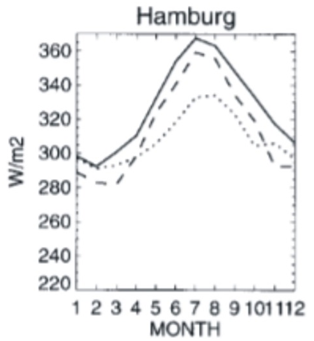
Figure 4 Back radiation from Wild et al.¹⁶ The measured values are the solid line. The dotted and dashed lines are computer simulations.

BR = WV ± CO₂ ± methane ± trace gases (4)

The signs are ± because they are negative when back radiation is warming the atmosphere as from January to July in Figure 1. From July to January, they are positive as back radiation is cooling the atmosphere.

Rewriting Equation (4) in favor of water vapor gives:

WV = BR ± CO₂ ± methane ± trace gases (5)

On the average July 1 at Hamburg, the warming effect of CO₂ = 0.6% of that of BR. From Figure SPM.5 of AR5, the warming effect of CO₂ is equal to the warming effect of methane plus the trace gases, i.e., 0.6% of BR.

Therefore, WV = BR ± (0.6% x 2) = BR ± 1.2%. Then, the warming by water vapour is approximately 98.8% of the measured value of BR, and the cooling is 101.2% of BR. Thus, the error in Figure 5 is ± 1.2%, which is essentially negligible.

Figure 5 the relationship between warming by water vapor and warming by CO₂.

Figure 5 is Figure 1 adapted to show the relationship between water vapour and CO₂. Diagrams of the Earth’s energy balance¹⁷ indicate the importance of water vapor by showing that on average one half of the sun’s energy reaching the Earth’s surface goes to evaporating water. The back radiation directed towards the Earth’s surface is twice the amount directly from the sun and all of it comes from water vapor. This is serious evidence that water vapor is controlling the Earth’s temperature and climate change.¹⁸

Evidence is obtained from applying the laws of physics, namely the gas laws, to the gases in the atmosphere that act as ideal gases to show that from winter to summer CO₂ provides a small cooling effect on the atmosphere and from summer to winter it provides a very small warming effect. At the same time, back radiation acts opposite to CO₂ and is warming the atmosphere while CO₂ is trying to cool it and vice versa. For example, from winter to summer, the warming effect of back radiation at Hamburg, Germany, increases by 70Wm^–2, from 298 to 368Wm^–2. At the same time, the concentration of CO₂ in dry air is falling by 29 ppmv from 403 to 377 ppmv and provides a small cooling effect of 0.40Wm^–2, which is 0.6% of the warming by back radiation. From summer to winter back radiation cools the atmosphere by 70Wm^–2 and the CO₂ provides a small warming effect of 0.40Wm^–2. In each situation, the effect of CO₂ is so small as to be negligible. Evidence is provided to show the same situation occurs from the Arctic to the Tropics.

Methane and the trace gases also have a similar small cooling effect from winter to summer and vice versa. The sum of their warming effect is the same as that of CO₂ (Stocker et al. 2013). Therefore, the warming and cooling effect of all of the greenhouse gases except that of water vapor is ±(2 x 0.06%) = ±1.2% of back radiation. The warming by CO₂ plus methane plus the trace gases is small enough to be negligible. All greenhouse gases can warm or cool the atmosphere depending on conditions. An example is shown for water vapor and CO₂ in Figure 5.

Typically, the annual inverse relationship between CO₂ and water vapor occurs daily. For example, at Montreal, Canada, on the average July 1 the concentration of CO₂ from 6 AM to mid–afternoon moves opposite to the temperature rise of 7°C and falls by 9.0 ppmv.

The laws of physics, namely the gas laws, are the key to understanding the very small, essentially negligible, effect that CO₂, methane and the trace gases have on atmospheric temperature and climate change. The gas laws give similar results regardless of the concentration of CO₂, methane and the trace gases in the atmosphere. From the results of this work, it is clear the government policies to curb fossil fuel consumption and thereby control climate change are ineffectual because CO₂ has virtually no effect on atmospheric temperature or climate.

It appears the gas laws as applied in this paper are not included in climate models. If they were included the models could not project continually increasing atmospheric temperature with increasing concentration of CO₂. Whether or not the models can be restructured for improved performance is beyond the scope of this study.

None.

Author declares there is no conflict of interest.

1. Stocker TF, Qin D, Plattner GK, et al. IPCC, 2013: Summary for Policymakers. In: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report (AR5) of the Intergovernmental Panel on Climate Change. UK: Cambridge University Press; 2013. p. 1–1552.
2. Lightfoot HD, Mamer OA. Back radiation versus CO₂ as the cause of climate change. Energy & Environment. 2017;28(7).
3. Keeling CD. The concentration and isotopic abundances of atmospheric carbon dioxide in rural areas. Geochimica et Cosmochimica Acta. 1958;13(4):322–334.
4. Keeling CD. The Concentration and Isotopic Abundances of Carbon Dioxide in the Atmosphere. Tellus. 1960;12(2):200–203.
5. Andrews EA, Kofler JD, Trudeau ME, et al. CO₂, CO and CH₄ measurements from tall towers in the NOAA Earth System Research Laboratory’s Greenhouse Gas Reference Network: instrumentation, uncertainty analysis, and recommendations for future high–accuracy greenhouse gas monitoring efforts. Atmospheric Measurement Techniques. 2014;7:647–687.
6. Houghton JT, Jenkins GT, Ephraims JJ. Climate Change 1990. UK: Cambridge University Press; 1990.
7. Houghton JT, Ding Y. Climate Change 2001. Working Group I: The Scientific Basis, Intergovernmental Panel on Climate Change, 2001, Third Assessment Report(TAR). USA: Cambridge University Press; 2001. p. 1–893.
8. Solomon S, Qin D, Manning M, et al. IPCC Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report (AR4) of the Intergovernmental Panel on Climate Change. UK: Cambridge University Press; 2007.
9. NOAA. Email messages from NOAA personnel contacted through the World Meteorological Organization, July 2016, re parts per million by volume being 0.3 ppm less than parts per million molecules at 400 ppm level of CO₂.
10. WMO. Meeting of Experts on Carbon Dioxide Concentration and Related Tracers Measurement Techniques WORLD METEOROLOGICAL ORGANIZATION GLOBAL ATMOSPHERE WATCH, 13TH WMO/IAEA. USA: World Meteorological Organization; 2007. p. 1–163.
11. The Engineering Toolbox, Altitude above Sea Level and Air Pressure, 2017.
12. Tans P, Thoning K. How we measure background CO₂ levels on Mauna Loa. USA: NOAA Earth System Research Laboratory; 2008.
13. MegaWatSoft Psychrometric Calculator, HumidAir Excel Add–In v3.1.
14. American Society of Heating, Refrigerating and Air–Conditioning Engineers, Inc. (ASHRAE).
15. Lightfoot HD, Mamer OA. Calculation of atmospheric radiative forcing (warming effect) of carbon dioxide at any concentration. Energy & Environment. 2014;25(8).
16. Wild M, Ohmura A, Gilgen H, et al. Evaluation of Downward Longwave Radiation in General Circulation Models. J Climate Amer Meteor Soc. 2001;14(15):3227–3239.
17. Stephens GL, Li J, Wild M, et al. An update on Earth’s energy balance in light of the latest global observations. Nature Geoscience. 2012;5:691–696.
18. http://www.climatechange2013.org/report/full–report/.