River diversion barrages are subjected to varying hydraulic conditions ranging from gate controlled and uncontrolled flows with possible free and submerged conditions on the downstream. The resulting scour of the downstream riverbed material, varying according to the specific combination of the hydraulic parameters, may be reduced by providing a depressed apron on the downstream of the usual stilling basin. This paper investigates the possible shapes that may be given to the normal block protection apron downstream of a barrage structure that may best reduce the extent of downstream scour. The effectiveness of this secondary apron in preventing the hydraulic jump from moving dangerously out of the stilling basin for exceptionally low tail water conditions is investigated.

Keywords: diversion barrages, apron, scour, hydraulic jump, stilling basin

River diversion barrages are commonly used in India, Pakistan, Egypt, and quite a few south Asian countries for diverting water into canals conveying water for irrigation though some canals convey water for hydropower generation or industrial and domestic water supplies. A diversion barrage, though serving the same purpose as a diversion weir or a diversion dam, is functionally different from either. Compared to the weir a barrage has gates guided by piers for better control of flow and maintenance of the level of water in the pond behind. In comparison to a dam a barrage differs in the type of construction which is designed as a raft floor in comparison to the gravity section of a dam. Further, the difference in water levels on the upstream and downstream of a barrage would usually be larger than that of a weir and smaller than that of a dam. These differences result in dissimilar hydraulics of flow through a barrage in comparison to that of a weir or a dam. Normally, a weir gets submerged during flood flows whereas a dam largely maintains free flowing conditions. The prevailing hydraulic condition for a barrage, on the other hand, depends upon the downstream river characteristics and the gate opening patterns.

Figure 1 shows the longitudinal section through a typical barrage bay adapted from CBIP.¹ Details of diversion structures are provided^2–5 describe the possible hydraulic situations that may arise for a diversion barrage and their consequences on the scouring downstream of the structure. Low head navigation dams encounter very similar hydraulic conditions as barrages^6–8 appropriately describes these along with design details.

Figure 1 Longitudinal section through a bay of the barrage on River Teesta, India.

It is generally recognized that flow regulating structures such as weirs, dams and barrages are subjected to local scour, especially on the downstream, due to the disturbance introduced to the normal flow of the river and consequence increase in the turbulence levels.⁹ Quite a good amount of work have appeared on the investigation of scour downstream of high head structures like dams and that below low head structures like sluices and weirs as apparent from publications.^10,11 However, studies on scour specifically downstream of barrages are rare though the nature of scour has strong similarities with those below sluices and weirs. Ghosh et al.⁵ discuss the variations in scour downstream of a barrage for all possible flow conditions and conclude that the flow with the gates completely opened and having low water on the downstream results in the most severe scour for a barrage. This condition, it may be mentioned, is not a common occurrence since at the time when there is low flow in the river with a consequent low tail water level the gates are normally controlled in order to keep the pond water level at the desired elevation. The exceptional situation may occur if a gate completely collapses during such a prevailing flow condition. More common flow situations encountered for a barrage includes low flows controlled by gates with corresponding reduced tail water or completely withdrawn gates passing flood flows with relatively high tail water.

Although flow situations and resulting scour variations downstream of barrages have been summarized by Ghosh et al.⁵ not many reports are available suggesting structural modifications to effect scour reduction. A good amount of work has been carried out investigating the scour below dams and energy dissipating systems have been proposed, some of which have been found suitable for specific barrages as well. The recommendations for the USBR stilling basins of types II and III by Bradley, et al.¹² included later on in Engineering Monograph 25 (USBR, 1958), are mostly suitable for the range of Froude number usually encountered for the flows through a barrage. However, the efficiency of a hydraulic jump type stilling basin is rather low, especially for low Froude numbers.¹³ Nearly 60 to 70 percent of the energy is conveyed downstream for a typical stilling basin the length of which is generally provided as five times the depth of tail water. The amount of residual energy can be reduced further by addition of friction blocks and other devices in the stilling basin, but a substantial amount of energy would still be available to cause local scour of the riverbed downstream. An interesting technique to dissipate some of this residual energy has been adopted in the design of the Qadirabad barrage on River Chenab in Pakistan (Figure 2). The concrete block apron, provided downstream of every barrage to release the seepage flows, has been shaped in the form of a triangular depressed basin. This method is not new but corresponds to the negative step provided on the downstream of a stilling basin.¹⁴ However, it is one of the rare cases where such a depressed basin has been provided downstream of a barrage apron. In fact, for none of the barrages in India has such a method been adopted. Though reported literature on this aspect is conspicuously lacking, Russian (former Soviet) designs of stilling basins downstream of low head dams resembling barrages demonstrate similar features.¹⁵ Commonly this depression is referred to as the “lower pool”. The basin shape in this case is trapezoidal. Nevertheless, no report is available on the studies that have led to the selection of this particular shape or for arriving at the particular dimensions. Though not exactly the same but the conduit outlets of dams are provided with a depression resembling a pre-formed scour hole the purpose of which remains identical.

Figure 2 Longitudinal sections through a bay of Qadirabad barrage on River Chenab, Pakistan.

This paper presents the results of an experimental program carried out for determining the optimum shape of a secondary depressed apron in reducing scour downstream of the stilling basin of barrages. Since the downstream scour would be inversely proportional to the length and depth of the secondary apron the relative proportions of the apron are estimated that may be economical yet practicable for construction.

Test program

The approach to arrive at a rational basis for the investigation is established on the basis of hydraulic model tests carried out at the Indian Institute of Technology at Kharagpur. The test program is divided into two parts. First of all, an optimum shape is selected from a range of profiles that would help to dissipate most of the residual energy and thus result in minimum scour. In the second step the effect of the relative proportions of the chosen basin is investigated vis-à-vis the reduction of scour. The hydraulic conditions used for the tests have been selected following the general guidelines provided by USACE⁶ a manual on the design of navigation dams, the hydraulics of which closely resembles that of a barrage. This manual mentions the checking of the normal as well as the emergency operating conditions. Normal operating schedules are those that result in approximately equal distribution of flow across the outlet channel. Such condition includes gated free and submerged flows and these have been used to arrive at the shape and proportions of the depressed apron. Additional tests have been carried out to investigate the effect of the depressed apron in reducing scour compared to a normal horizontal apron for emergency conditions that result from the malfunctioning of one gate, when the gate gets stuck at a particular opening, or its complete collapse. This condition, which results in uncontrolled through the bay, is tested for both low and high tail water levels. A peculiar condition, not specifically mentioned by USACE⁶ has been noticed in some barrages in India and has been tested as well. This situation has been observed to develop at times with only a few gates opened during low flows. In this case, the tail water level had been low as well resulting in a free hydraulic jump on the stilling basin. With slight increase of discharge, inadvertently, the same gates that were open have been opened further to maintain the pond level. Since the tail water level would have hardly changed at this stage, it has resulted in the jump being pushed down further downstream, shooting below the edge of the stilling basin. Since the normal concrete block apron just downstream of the stilling basin is loosely held in place with purposeful gaps in between to allow release of seepage flows, the sand particles were sucked out by the high turbulence resulting in sinking of many of these blocks. Also, the scour of the riverbed downstream has been exceptionally high. This condition is reproduced in the present experiments and the effectiveness of the depressed apron in containing the hydraulic jump is tested.

Test apparatus

The test apparatus primarily consisted of a hydraulic flume measuring 13.5m in length, 0.59m in width and 0.71m in depth. A typical profile of a model barrage weir and aprons were prepared in light cement concrete. For visual inspection, one side of the flume was made of glass. The flow was controlled by a vertical lift gate, which is usual for diversion barrages in India. The water supply from the upstream was through a constant head water tank equipped with a calibrated V-notch. The tail water was controlled by an adjustable tail gate. The test section was located at 6.15m from the upstream of the flume. Downstream of the depressed apron a sediment recess was provided, the length and depth of which was based upon the expected maximum scour on the downstream. A sediment trap was provided just downstream to arrest the material washed out from the sediment recess. A longitudinal section of the test section is provided in Figure 3. The sand used as the bed material for the experiments had a relative density of 2.65 and characteristic d₅₀ of 0.23mm .The geometric standard deviation, s_g defined as s_g = (D₈₄/D₁₆)^0.5, was equal to 1.30 and the porosity 0.492.

Figure 3 Longitudinal section through test section of experimental setup.

Test procedure

For evaluating the best shape of the depressed secondary apron in reducing the residual energy flowing out of the stilling basin apron and consequent scour, a few profiles were conceived considering the ones already known or cited in the references. The horizontal form (Figure 4a) is the standard normally adopted as shown in Figure 1. The triangular shape (Figure 4b) derives from the shape provided at Qadirabad barrage (Figure 2). This shape intuitively resembles, albeit in a piecewise linear fashion, the basic scour profile downstream of barrage structures. However, a few variations (Figure 4c and Figure 4d) are also tested. Figure 4e represents an extreme case of the triangular shape where the vertex is moved to align with the downstream vertical sheet pile provided at the edge of the stilling basin. The trapezoidal profile (Figure 4f) is adapted from the shapes provided in Russian designs.¹⁵

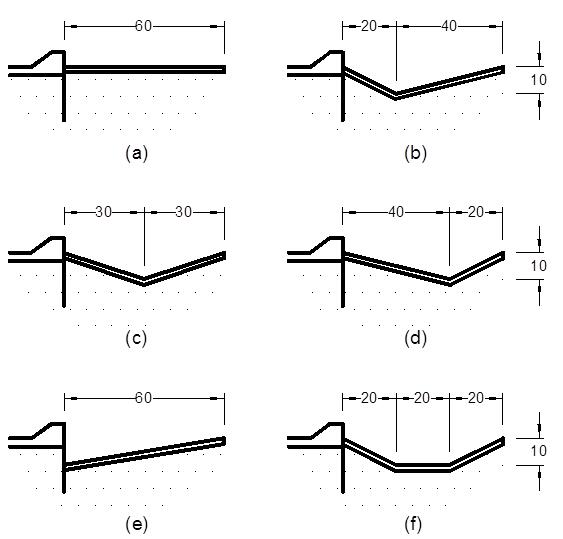
Figure 4 Shapes of depressed apron tested (a) Horizontal; (b) 1/3-2/3 triangular; (c) 1/2-1/2 triangular; (d) 2/3-1/3 triangular; (e) Inclined; (f) Trapezoidal.

Each of these shapes are tested for the same length and depression values with constant discharge but two tail water levels, one low and the other high,  that produce free and submerged hydraulic jump conditions respectively. The resulting scour profiles are recorded with the maximum scour depth being used for the comparison between the profiles.

The second stage of finalizing the relative dimensions of the selected shape involves testing different lengths and depression values under similar hydraulic conditions. The resultant scour profiles and flow variables at certain sections are recorded and compared with the case where a secondary apron is absent on the downstream of a stilling basin.

Lastly, the effectiveness of a depressed apron in containing the hydraulic jump is tested for the emergency conditions mentioned earlier. This exceptional condition is simulated by increasing the gate opening together with the discharge while maintaining the upstream water level. The tail water is maintained at a low level. The tests conclude with the extreme case of a completely withdrawn gate. The extent of scour for each condition is compared for a stilling basin having a secondary apron that is horizontal with that having a depressed apron.

The results of the tests and the inferences drawn there from are summarized in this section.

Selection of the best shape of depressed apron

The scour profiles obtained for the different shapes are shown in Figure 5 and Figure 6 for free and submerged flow conditions respectively. From a comparison of the maximum observed scour depths in each case (Table 1) it is observed that the 1/3-2/3 triangular depression registers the minimum scour under both conditions. Of course, the scour reduction by the trapezoidal depressed profile is marginally smaller than that of the 1/3-2/3 depressed profile under both free and submerged jump conditions. However, the latter requires a larger excavation work than the former. Hence the 1/3-2/3 depressed triangular profile, referred to simply as the triangular depressed apron in the rest of this paper, is tested for further analysis to determine the optimum length and depression value.

Figure 5 Comparison of scour profiles under free hydraulic jump condition for different depressed apron shapes. All measurements in cm.

Figure 6 Comparison of scour profiles under submerged hydraulic jump condition for different depressed apron shapes. All measurements in cm.

Efficiency in reduction of scour by the triangular depressed apron

Though it is apparent that a secondary apron would generally provide protection against scour if its length and depth are increased, it is of importance to know which combination of depth and depression would provide the most optimum reduction in scour. A deeper and longer depressed apron would necessitate both increased excavation as well as greater construction cost. Further, deeper aprons would also require steeper slopes, which may not be suitable for construction for all types of riverbed material. In order to estimate the relative effectiveness in reducing scour, the maximum scour depth by a range of depths and lengths of triangular apron is compared with that without any apron. The details of the proportions of the secondary apron shaped in the form of a 1/3-2/3 triangular depression is presented in Table 2.

The reduction in scour by the 1/3-2/3 triangular secondary apron for each configuration from that of a situation without an apron expressed in percentage is presented in Figure 7 and Figure 8, respectively.

Figure 7 Percent reduction of the maximum depth of scour under controlled free-flow condition by the 1/3-2/3 triangular secondary apron compared to that without an apron.

Figure 8 Percent reduction of the maximum depth of scour under controlled-submerged flow condition by the 1/3-2/3 triangular secondary apron compared to that without an apron.

From an observation of the graphs (Figure 7 and Figure 8), the following conclusions may be drawn:

The following observations may be may be concluded from a study of the scour profiles and maximum scour depths produced by the different depressed aprons.

1. The profile of the scoured bed for the horizontal apron is much larger than any of the depressed aprons for both free and submerged flow conditions (about 30 to 50 percent compared to the minimum).
2. The scour reduction by the 2/3-1/3 triangular profile is the least compared to that of the other depressed aprons under both free and submerged flow conditions.
3. The reduction of scour under free flow condition is less than under submerged conditions by all the depressed aprons.
4. Under free flow conditions, the reduction in maximum scour is greatest by the 1/3-2/3 triangular profile, though being marginally more than that by the trapezoidal profile.
5. Under submerged flow conditions, the reduction in maximum scour is greatest by the adverse incline followed by the 1/3-2/3 and 1/2-1/2 triangular profiles.

It may, therefore, be concluded that there is no single profile of depressed apron that fares best in reduction of maximum scour under both free as well as submerged conditions. However, the 1/3-2/3 triangular and the trapezoidal profiles perform nearly equal well under both conditions. The adverse incline, though proving superior to others under submerged conditions, achieves the minimum reduction in scour of all depressed aprons under free conditions.

It thus seems logical to choose a final form from amongst the 1/3-2/3 triangular and the trapezoidal profiles. However, the former may be selected for adoption as the optimum shape of depressed apron for barrages for the following reasons:

1. The excavation of the 1/3-2/3 triangular profile is less compared to that of the trapezoidal profile.
2. The shape of this profile provides the closest match with the generic shape of scour holes observed on the downstream of barrages and similar structures like weirs and sluice gates.

In order to investigate the reason behind the reduction in scour by depressed secondary aprons in comparison to that of the horizontal apron, a comparison of the flow variables was made for the 1/3-2/3 triangular profile and compared to that of the horizontal profile, as described in the following section.

1. For the range of lengths and depths of the triangular apron tested for reduction of scour, the characteristics of reduction are nearly similar for both free and submerged flow conditions. This implies that variation in tail water depth does not significantly alter the efficiency in scour reduction.
2. The typical shape of the graphs show that for transforming a horizontal apron into a 1/3-2/3 triangular depressed apron, a change of the depth matters more in reducing scour for longer aprons than for shorter ones.
3. The reduction of scour for both free and submerged conditions range from zero (for the shortest horizontal apron) to about 50 percent.

It may be mentioned here that the above comparisons for reduction in scour by the depressed apron with respect to the horizontal apron have been conducted for gate-controlled flows. In practice, however, a barrage is likely to pass uncontrolled flows (that is, with full gate withdrawn) especially during the passage of floods. Since simulation of such conditions required very high discharge, these could not be tested. It is presumed that the efficacy in reducing scour under such conditions would be similar to the ones obtained for the gate-controlled conditions.

Effectiveness of depressed apron in containing the position of hydraulic jump

As mentioned previously, at times of low flows with corresponding low tail water, increasing discharges through a few bays of a barrage may displace the hydraulic jump further down from its normal zone of occurrence, that is, the downstream slope of the weir. Since both the stilling basin as well as the downstream concrete block apron are generally both placed horizontally, the hydraulic jump changes to an unstable state with its location fluctuating and moving down even as far as up to the loose riverbed depending upon the intensity of discharge and position of tail water. Though happenings of this kind is rare, caused mostly by unintended wrong operation of gats, a few cases have been reported which has led to the hydraulic jump causing enormous scour to the unprotected riverbed downstream. It was believed that a depression downstream of the horizontal stilling basin would not have allowed the jump to move further down, thus limiting the scour. This aspect was tested by comparing the scour downstream of a normal combination of a horizontal stilling basin and a horizontal secondary apron with that having a depressed apron downstream of a horizontal stilling basin under different discharges and a constant low tail water level.

Barrage hydraulics under low tail water level conditions

Low tail water levels for a river diversion barrage, occurring during minimum flows in the river, may sometimes produce adverse flow situations. When such flows take place through a nearly completed barrage, with the gates yet to be installed, the upstream water level of the barrage is correspondingly small, there is practically no obstruction to the flow except for the weir crests of the spillway bays and the presence of the piers in between the bays. Hence, the water level on the upstream of the barrage differs nominally from the tail water level for any discharge. This difference, called the afflux, is the amount of water head required to pass the river discharge through the barrage structure. Normally, because of the low crest heights of the weirs, submerged flow conditions exists under such situations, and hence not much adverse scouring is expected to occur on the downstream. Increasing discharges lead to both higher tail water as well as head water levels and therefore, do not pose a serious threat to downstream scour. The situation changes when the gates of the barrage are installed and are brought into operation to control the outflowing discharges. At this time, even for low river discharges with corresponding low tail water levels, the mandatory pond level is required to be maintained. Such situations of gate-controlled flows apparently produce significantly larger local scour of the unprotected riverbed immediately downstream of the barrage stilling basin and secondary apron compared to that during flood discharges when almost all the gates are completely opened.⁵ Of course, during flood discharges the general scour, that is the overall lowering of the riverbed on the downstream, is expected to be more.

Since the effect of tail water level variation on downstream scour has been amply investigated⁵ this study extends it further by studying the effect of tail water level on the stability of the barrage structure, especially the downstream concrete block apron. In fact, it may be intuitively concluded that the flow situations leading to dangerous scour condition for a barrage may also be equally threatening for the stability of the concrete block apron.

This section attempts to identify the occurrence of such a condition for a prototype barrage, taking the barrage on River Mahanadi as a typical case. Following this, the results of the experiments conducted to investigate the effect of low tail water levels on the stability of concrete block apron as observed from experiments on a physical hydraulic model replicating one bay of a typical barrage gate are presented.

Theoretical study of the hydraulics for Mahanadi Barrage, India

The water level, or gauge, versus discharge graph (G-Q curve) at the site of the Mahanadi Barrage adapted from Patel¹⁶ is presented in Figure 9. It may be observed that the initial G-Q was expected to hold good within a range that was based upon the data of initial years. A mean G-Q curve passing the range appears to have an accuracy of about ±0.25m for any discharge value. The peak flow data of later years corresponding to the post-completion phase of the barrage, however, have shown a downward shifting trend. This phenomenon of a retrogressed river bed level is mostly observed for barrages constructed across rivers carrying relatively less sediment load. For those on rivers carrying rather high sediment along with their flows, the phenomenon may not be observed. For the case of the Mahanadi Barrage, the resulting G-Q curve appears to differ from the original mean curve by about 1.5m on the lower ranges of discharge and by about 0.75m on the higher ranges.

Figure 9 Gauge versus discharge curves at the site of Mahanadi Barrage.

Considering the fact that the Mahanadi Barrage consists of sixteen undersluice bays and seventy-nine spillway bays with respective crest and cistern level, it is possible to recreate the G-Q curve for the barrage prior to gate installation and flow control. This is shown as the lowermost curve of Figure 9 in which the initial G-Q curve of River Mahanadi is used to corresponding to the tail water (that is, the downstream) level. The water level of the pond on the upstream of the barrage corresponding to the discharge and water levels of the downstream values have been computed using standard discharge coefficients for unobstructed (ungated) flow over spillway as available in texts. Of course, the different crest heights of the undersluice and spillway bays have been taken into account as well as the effects of the respective cistern (stilling basin) level elevations and tail water submergence on the flow. However, it is important to note that though relations are available for ogee shaped spillway crests (as provided in dams) there is no general relation available for obtaining the theoretical discharge coefficient for the spillway of barrage with its typically inclined upstream and downstream weir glacis. As such, these need to be ascertained from model studies on case to case basis. Ranga Raju¹⁷ presents relations for discharge coefficients for weirs with sloping glacis, but the upstream and downstream floors have been considered at the same level. USBR (1987) provides, however, very comprehensive discharge coefficient curves and their variations with different parameters like downstream apron level, tail water level, etc. for ogee shaped spillways. For the short weir heights of within 3m above the downstream cistern for the Mahanadi Barrage, it was felt that the ogee shaped spillway discharge coefficients as provided by USBR (1987) would not produce much error and was adopted for the computation of the G-Q curves. The resulting curve is shown in Figure 9, which indicates that the afflux for the unobstructed free flowing discharge through the barrage is only about 0.3m for the higher discharges.

It may be noted that once the gates of the barrage are brought into operation, water level behind the gates is elevated to the mandatory Pond Level, the designed value of which for the Mahanadi Barrage is 21.2m. This water level corresponds to about 6000m³s^-1 of the initial G-Q curve and the variation of water level in the pond may be represented by a horizontal line as shown in Figure 10. This level is maintained for increasing river discharge by gradually increasing the gate openings till all gates are completely opened, in this case for discharges higher than 6000m³s^-1.

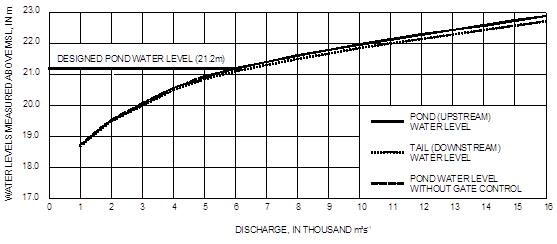
Figure 10 Variation of water levels on the upstream and downstream of Mahanadi Barrage, prior to retrogression.

It may be pointed out that the barrage water level regulation curves (Figure 10) was developed using the initial G-Q relation of the River Mahanadi. However, as Figure 10 shows, there appears to have been substantial retrogression of the riverbed from its original position prior to barrage construction. Hence, a revised curve for barrage water level regulation was computed, which is presented in Figure 11.

Figure 11 Variation of water levels on the upstream and downstream of Mahanadi Barrage, post retrogression.

From a study of the Figure 10 and Figure 11, it may be observed that under the present river conditions, the designed pond level of 21.2m corresponds to nearly 10,500m³s^-1, beyond which the gates would normally be completely withdrawn. However, if the barrage management authorities feel, all the gates may be withdrawn even for discharges lower than 10,500m³s^-1, and in that case the pond level would consequently be lowered. As shown in Figure 11, the pond level would drop from the point A to the point B if all the gates are completely withdrawn for a typical discharge, say, 7000m³s^-1. However, in case all the gates are not completely opened but a large enough opening of some of the gates are provided to pass more than 7000m³s^-1, then the pond level would probably vary along a path A to D. Beyond D, all the gates would be completely opened and the pond level would be higher than the tail water level by an amount equal to the afflux corresponding to the discharge.

The decision to lower the pond level than the design value depends upon the expected inflows and has to be decided by the barrage management authorities. For the River Mahanadi flood mentioned earlier (discharge hydrograph shown in Figure 9), it appears that a similar barrage water level regulation pattern was followed as may be observed from Figure 12. In fact, from the July 10, 1994 up to the July 11, 1994 it appears that the gates were completely withdrawn in view of the rising flows. Beyond July 25, 1994 the gates were again brought into operation, as is obvious from the rising pond level in spite of the receding tail water level. However, the pond level beyond 25^th appears not to have recovered fully to the designed value.

Figure 12 Gauge hydrograph for the flood of 1994 in River Mahanadi showing variation of water levels on the upstream and downstream of barrage.

Identifying the critical hydraulic condition with low tail water level

It may be inferred from the discussions in the preceding section that even for high flood discharges the correspondingly high tail water levels submerge the flow over the barrage crests, thus causing relatively low Froude number of the flow outflowing on the downstream (as for the period July 11, 1994 to July 25, 1994). For low flows (for example from July 2, 1994 to July 9, 1994), on the other hand, the high pond levels with a possibly free (un-submerged) flow on the downstream cause a shooting flow to emerge through the opened gates which form a violent hydraulic jump as it meets the corresponding low water level on the downstream. It is under such circumstances, that the hydraulic jump may move down farther from the stilling basin, thus affecting the stability of the concrete block apron further downstream.

Effect of low tail water level on the structural stability of barrage components

The flow through barrage gate bays would be governed by the usual conditions expected under the normal range of operating conditions. This would include low flows when a few gates remain opened, the extent of opening decided by the pond level that is required to be maintained and the flow that is to be released downriver. Under such conditions, the water level on the downstream is usually low corresponding to the gauge-discharge relation of the river downstream of the barrage. However, an emergency condition that may arise at this stage is the sudden collapse of a gate as that happened for one of the gates of a barrage on River Ganges in the State of West Bengal, India in December 2000. The breakdown was sudden and did not provide ample prior indication to lower the emergency stop logs. Further, the water level difference between the upstream pond and the river downstream was relatively large (around 5m), which did not permit the installation of the logs under the rushing torrent of water through the gate bay. As a result, it was quite some time (in days) before any remedial measure could be taken up. When the flow was finally controlled with the erection of a new gate, substantial damage to the concrete block apron had already been done.

The high flows also did not permit correct observation of the water levels on the stilling basin or the downstream secondary (concrete block) apron but it was generally agreed that the hydraulic jump had shot out of the former and formed over the latter or even beyond. The damage to the block apron, assessed after the flow through the gate was brought under control, was found to be extensive with no trace of most of the concrete blocks which had either sunk or had got carried downstream. Rather, a gaping local scour hole remained in its place which had to be filled up later with sand bags, though not up to the original level of the block apron. Although the undisturbed floor level of the concrete block apron normally varies between the elevation of the stilling basin apron and the end sill crest elevation, recommendations for rehabilitated secondary aprons suggest maintaining a lower floor elevation of the replacement as this would act like an abrupt-drop secondary apron USACE⁷ which might come in useful in future for stabilizing a hydraulic jump in case of a repetition of the shootout incident of the jump.

The extent of damage to the secondary (concrete block) apron may not be generalized as it would depend upon the flow passing through the gate bay, the tail water level, the time for which the flow is likely to sustain, etc. and would thus vary from case to case. Again, a complete collapse of a gate at the time of low tail water level may not be the only cause for damaging the concrete block apron downstream of a barrage stilling basin. A malfunctioning gate that has wedged itself between the guide rails at a certain opening may also lead to unrestricted, albeit gate controlled, flow. It may be mentioned that the United States Army Corps of Engineer’s guidelines on the design of navigation dams (low head dams quite similar to river diversion barrages in function) recommend additional checks for the design of the stilling basin under both fully opened gate and half-open gate (partially controlled flow) conditions under possible low tail water levels. Probably such a strategy would ensure a safe design of the stilling basin and the downstream secondary apron under all possible operating conditions. However, the Indian guidelines for barrage design BIS¹⁸ does not recommend the inclusion of such conditions, and may thus be said to have adopted the design philosophy of providing only for the normal conditions and leaving out the extremes. Risks remain but designing for the exceptional conditions would lead to a consequential increase in project cost. Rather, it is felt that a stilling basin may be designed for the normal operating conditions and the stability of the secondary concrete block apron checked for the possible exceptional flow conditions in assessing a prior estimate of possible damage.

It is for this reason that a need was felt to investigate the stability characteristics of the concrete block apron under low tail water situations under different gated and ungated flow conditions. The experimental programme of which is presented in the following section. It may be noted that although similar studies have apparently not been conducted so far for barrages, there exist reports on the effect of shooting flows over the stilling basin of high head dam spillways.¹⁹ A perusal of these references indicates the presence of high pressure fluctuations which may cause cavitation damage to the stilling basin floor. Though barrages may not be subjected to such extreme flow conditions, the negative pressure fluctuations of shooting flows may be strong enough to dislodge some of the concrete blocks.

Experiments to study the effect of emergency conditions on the stability of concrete block aprons

For studying the effect of low tail water level on the stability of concrete block aprons, it was hypothesized that the stability would depend upon the flow pattern governed by the discharge, gate opening, tail water level, etc. Following Mossa et al.,²⁰ the flow pattern may be considered to be a function of the inflow Froude number, relative depths of the tail water and the pre-jump depth and the step height of a depressed apron. However, since it is normal to provide a horizontal secondary apron at almost the same elevation as the stilling basin or the end-sill crest, there was no requirement of considering a step height and only the first two parameters were judged to be influential in defining the flow pattern. These parameters were varied by changing the inflow discharge, the gate opening and the tail water level.

The dimensions recommended for prototype concrete blocks by the Indian standard for barrage design BIS¹⁸ is1.5m x 1.5m x 0.9m. Considering a typical prototype gate bay width of 20m and the model bay width of 0.6m, the model concrete blocks were prepared to a size of 0.045m x 0.045m x 0.025m. Three discharge values were tested and the gate opening for each discharge varied from a minimum to a fully withdrawn gate. Only two significantly low tail water levels as possible for the setup were considered. Higher tail water levels reduced the exit flow velocity and consequently the displacements of the concrete block aprons were reduced. The concrete block apron was laid over a 0.5m layer of sand with mean diameter (d₅₀) 1.0mm. The length of the block apron was arbitrarily kept equal to that of the horizontal portion of the stilling basin apron (0.6m) as the recommended prototype length depends upon the design flood flows and would thus vary for each project. The parameters used for the experiments are summarized in Table 3.

Because of very low tail water levels, the water depths over the apron and on the downstream were also correspondingly small, which did not allow measurement of point velocities with the help of the Acoustic Doppler Velocity (ADV) measurer. However, from the water surface profile, it was possible to infer the average velocities at different locations of the flow domain. Each experiment was run for 2 hours and on completion, the displacements of the concrete blocks making up the apron was noted along one row along the flow direction. A typical flow situation for the experiments is shown in Figure 13 where a hydraulic jump is seen to form over the undisturbed configuration of the block apron. The governing flow parameters used in the analysis have also been shown in the Figure 13 and represent the depth of water just before the end-sill (y₁) and that above the secondary apron (original) level (y₂). The Froude number at the location of the depth y₁ provides another important governing parameter (Fr₁).

Figure 13 Definition of flow variables before and after jump.

In all 28 experiments were conducted. The following sections describe the results obtained from the above experiments.

Sinking and displacement of the concrete blocks of the horizontal secondary apron under low tail water level conditions

From studies on low tail water level effects on the formation of hydraulic jump over abrupt drop and negative step aprons^21–24 the possible hydraulic jump types were first recognized that is likely to form over the concrete block apron. Since the elevation of this secondary apron is rather high, it does not really represent a negative step. However, as each experiment progresses the blocks get displaced or disturbed due to the removal of sediment from below the blocks through the interstitial spaces within the blocks and the pattern of the flow profiles conform to the types already recognized in literature, as shown in Figure 14.

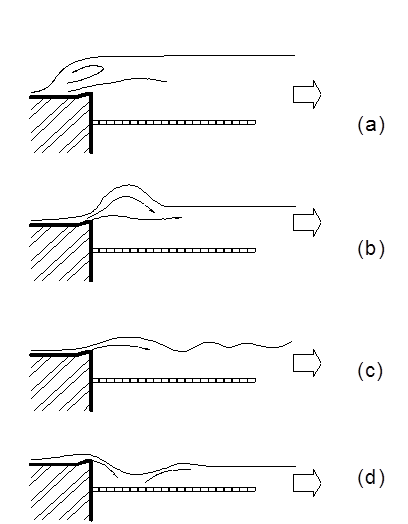
Figure 14 Flow profiles as observed with progressive lowering of the tail water level over a horizontal apron (a) Hydraulic jump over stilling basin; (b) Jump with surface roller and formation of a maximum wave; (c) Wave train; and (d) Plunging condition. (Note: the horizontal block apron has been shown lowered as happens with the passage of time).

Based on the above flow conditions, the flow regime for the hydraulic jump forming downstream of stilling basin and over a secondary apron was classified from the range of observed data as shown in Figure 15. Incidentally, for some of the experiments a few concrete blocks got displaced and were washed away downstream. The corresponding experimental points have been located by the shaded zones in Figure 16. In the experiments where this phenomenon took place it was noticed that displacements happened at quite an early stage of the model run and once the blocks had got dislodged, the underlying sand was sucked out by the fast flowing water leading to the sinking of the other blocks.

Figure 15 Flow regimes corresponding to the profiles shown in Figure 17.

Figure 16 Flow regimes indicating locations of block displacement and sinking.

It is important to note that even in those experiments which did not record sweeping out of the blocks, the prevailing flow condition gradually lifted up the underlying sand through the gaps between the block, thus sinking the blocks further into the sand below. From an analysis of the data, it was noticed that almost all the experiments where the blocks had been swept away were located within Zone (c) of the flow regime diagram (Figure 16). Also, the experimental points which recorded the maximum extent of sinking of individual blocks were located in the neighborhood of the imaginary line separating Zones (c) and (d).

The point that recorded the maximum sinking, either for a single block or the average for a group of blocks in any single experiment, is indicated in Figure 16. The numbers corresponding to this point indicate the maximum depth of sinking of a single block (10.03) and the average depth of sinking of the blocks (5.60) each non-dimensionalised with respect to the inflowing water depth, y₁.

Conclusions drawn from the experimental study investigating effect of low tail water levels on stability of horizontal secondary apron

From the observations the following conclusions may be drawn:

Low tail water levels may cause sweeping out of the hydraulic jump from the stilling basin onto the downstream secondary apron. The form of the water surface profile closely resembles that reported for low tail water level flows over negative steps. Low tail water levels causing water to flow in the “wave train” regime is seen to cause maximum damage to the concrete block apron by dislodging a few pieces completely and washing them downstream. In comparison, smaller tail water levels (resulting in plunging flow) and larger (generating the normal hydraulic jump over the stilling basin) do not cause the blocks to dislodge though they may sink into the sand as the flow continues.

Performance of depressed apron under low tail water level conditions

It is established that a depressed secondary apron is likely to reduce the scour on the downstream of a barrage structure. However, the flow conditions considered for the tests, which are generally considered for prototype barrage design as well, are the normal operating conditions for a barrage under high flood flows with or without the following additional conditions:^4,18

1. Flow concentration (to an extent of 20 percent) on the upstream pond leading to a higher discharge through some bays
2. Riverbed retrogression on the downstream.

It may be noticed that low flow condition is not considered for barrage design since the expected general riverbed scour is more during the above conditions. As mentioned previously, extraordinary or emergency flow conditions have not been recommended for barrage design yet (for example, in BIS). There have been instances where such situations led to substantial damage on the downstream of a barrage, especially to the loose concrete block apron downstream of a stilling basin. However, as concluded from the preceding section, depressed aprons are seen to reduce the downstream scour significantly, and hence it was hypothesised that such an apron may also be relatively more stable under such emergency flow situations compared to horizontal aprons. Hence, it was felt quite convincingly that a concrete block secondary apron shaped in the form of a depression would certainly be much stable under the extreme flow situations. With such a view to explore the stability of depressed aprons under low tail water level conditions, experiments were conducted.  Only one depressed shape was tested, that of the 1/3-2/3 triangular form, which was found to provide maximum reduction in downstream scour.

Experiments to study the effect of emergency conditions on the stability of depressed concrete block aprons

Small concrete blocks of size 0.045mx0.045mx0.025m were used as was done for testing the stability of the horizontal apron. The apron length was kept the same as that of the horizontal apron tested, that is, 0.6m. The 1/3-2/3 depressed apron with a depression of 0.01m was placed over a 0.5m layer of sand of with mean diameter (d₅₀) 1.0mm. The flow parameters considered were similar to those taken for the horizontal apron, as shown in Figure 17.

Figure 17 Definition of flow variables before and after jump for the depressed apron under low tail water level conditions.

The range of flow parameters were kept the same as those for the horizontal apron (Table 3). The following section discusses the results obtained from the above experiments.

Sinking of the concrete blocks of the depressed secondary apron under low tail water level conditions

The patterns of flow profiles observed from these tests (Figure 18) were quite similar to those obtained for the horizontal apron (Figure 14). It was observed that the extent of sinking of the concrete blocks making up the secondary apron was dependent upon the flow regime, as demarcated on a non-dimensional graph of the inflowing Froude number and relative ratio of outflow and inflow depths (Figure 15). Though exactly the same flow conditions were tested for the depressed secondary apron as were done for the horizontal apron, there were no displacement or wash outs of the blocks under the shooting flow of any of the flow regimes. As expected, the depressed form of the secondary apron slowed down the water flow over the apron and resulted in only sinking of the blocks. Again, the maximum sinking was also much smaller in this case compared to that observed for the horizontal apron. The experimental data point that recorded higher values of sinking of one individual block or the average of all the blocks along a row aligned in the flow direction are indicated in Figure 19. As depicted for the experiments with horizontal apron, the numbers in the Figure 19 corresponding to each point indicate the maximum depth of sinking of a single block and the average depth of sinking of the blocks, non-dimensionalised with respect to the inflowing water depth, y₁.

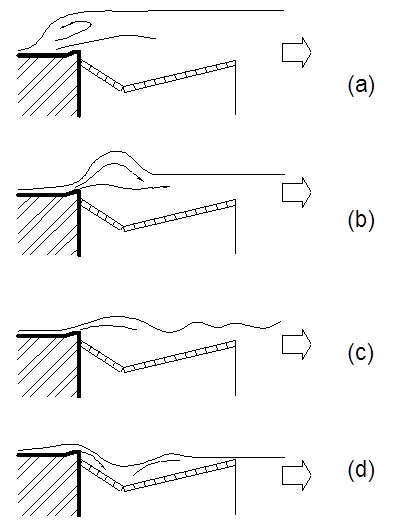
Figure 18 Flow profiles as observed over a depressed apron (a) Hydraulic jump over stilling basin; (b) Jump with surface roller and formation of a maximum wave; (c) Wave train; and (d) Plunging condition.

Figure 19 Flow regimes indicating points with high values of block sinking.

Conclusions drawn from the experimental study investigating effect of low tail water levels on stability of depressed secondary apron

Under the range of experimental conditions tested, there was no wash out of concrete blocks of the depressed secondary apron, which appears to be a very significant advantage over horizontal aprons.

The “wave train” flow regime (Figure 18 and Zone c of Figure 19) appears to be the most dangerous condition for block displacements.

The maximum individual displacements of the blocks appear to have been reduced considerably. The average block displacement is also significantly less compared to that observed for the horizontal apron.

On the whole, the above experiments and observation made in different study lead us to believe that a depressed apron helps to reduce the extent of downstream scour for exceptional conditions that may occur for a barrage and secondary concrete block aprons would indeed be stable, if provided in the form of a depression as that of the 1/3-2/3 triangular profile.

None.

The author declares there is no conflicts of interest.

1. CBIP. Barrages in India. Publication 148, Central Board of Irrigation and Power, New Delhi, India. 1981.
2. Leliavsky S. Irrigation and Hydraulic Design, Volume-1: General Principles of Hydraulic Design. Chapman and Hall, London. 1955.
3. CBIP. Manual on Barrages and Weirs on Permeable Foundation. Publication No. 179, Volumes I and II, Central Board of Irrigation and Power, India. 1985.
4. Novak P, Moffat AIB, Nalluri C, et al. Hydraulic Structures. Taylor and Francis, London, New York. 2007.
5. Ghosh MK, Kumar G, Sen D. Study of downstream scour for river diversion barrages. Proceedings of the Institution of Civil Engineers, Water Management. 2009;162(5):309–319.
6. USACE. Hydraulic Design of Navigation Dams. Engineering Manual EM 1110-2-1605, U. S. Army Corps of Engineers. 1987.
7. USACE. Guide for repairing scoured areas below navigation dam stilling basins and spillway aprons. REMR document HY-N-1.3, U. S. Army Corps of Engineers. 1987
8. United States Army Crops of Engineers. Hydraulic Design of Navigation Dams. USACE EM 1110-2-1605, 1991;259–284.
9. Escarameia M. River and Channel Revetments: A design Manual. Thomas Telford, UK. 1998.
10. Breusers HNC, Raudkivi AJ. Scouring, Hydraulic Structures Design manual Number 2.Balkema. 1991.
11. Hoffmans GJCM, HJ Verheij. Scour Manual. A A Balkema, The Netherlands. 1997.
12. Bradley JN, Peterka AJ. Hydraulic Design of Stilling Basins. Journal of Hydraulics Division. 1957;83(5):1401–1406.
13. Rajaratnam N. Almanac of energy dissipation mechanisms in Energy Dissipators. In: Vischer DL, Hager WH, editors. IAHR/Balkema, Netherlands. 1995.
14. Hager WH. Stilling basins in Energy Dissipators. In: Vischer DL, Hager WH, editors. IAHR/Balkema, Netherlands. 1995;61–88.
15. Grishin MM. Hydraulic Structures, Volume-1. Mir Publishers, Moscow. 1982.
16. Patel CC. Operation and Maintenance Manual of Mahanadi and Birupa Barrages. Department of Water Resources, Govt. of Orissa, India. 1989.
17. Ranga Raju KG. Open Channel Hydraulics. Tata McGraw Hill, New Delhi, India. 1993.
18. BIS. IS: 6966 (part 1) - Hydraulic Design of Barrages and Weirs – Guidelines, Bureau of Indian Standards, New Delhi, India. 1989.
19. Khasturia RM. Hydraulics of Spillways and Energy Dissipators. Marcel Dekker, New York. 2005.
20. Mossa M, Petrillo A, Chanson H. Tail water level effects on flow conditions at an abrupt drop. Journal of Hydraulic Research. 2003;41(1):39–51.
21. Moore WL, Morgan CW. Hydraulic jump at an abrupt drop. Journal of the Hydraulics Division. 1957;83(6):507–524.
22. Hager WH, Kawagoshi N. Hydraulic jumps at rounded drop. Proc. Institution of Civil Engineers. 1990;89:443–470.
23. Ohtsu I, Yasuda Y. Transition from supercritical to subcritical flow at an abrupt drop. Journal of Hydraulic Research. 1991;29(3):309–328.
24. Chanson H, Toombes L. Supercritical flow at an abrupt drop: Flow patterns and aeration. Can Journal of Civil Engineering. 1988;25(5):956–966.