The Marangoni effect is a very important phenomenon happening at an interface between two immiscible fluids creating a source of convection. This effect is very important in two phase flow problems. Unfortunately, the Marangoni effect is neglected by many studies in two phase fluid flow and is still considered a challenging problem.

A mathematical model has been developed in this paper showing the Marangoni effect in the case of two immiscible fluids in Navier-Stokes equation. The mathematical translation of the convection term at the interface is developed in detail from the starting point of physical parameters using powerful mathematical tools.

Keywords: marangoni effect, two-phase flow, interface, navier-Stokes

The Marangoni effect is happening at the interface between two immiscible fluids. In the absence of initial velocity, the movement of an interface is caused by a variation of interfacial tension; the displacement is the direction of positive superficial tension gradient.

The Marangoni effect is present in many domains in the instability problems in fluid mechanics,¹ microstructure problems² two phase flow problems,³ engineering flows in microfluidic devices⁴ and so many other domains. In the ink-jet problems,⁵⁻⁷ in 3D printing technology,⁸ these processes are complex because of physicochemical dynamics that arise from Marangoni effects, also in Surface patterning,⁹ interactions between suspended particles and a solid substrate.¹⁰

To understand and to show the mathematical aspect of the Marangoni effect at an interface between two immiscible fluids, we are going to build the one fluid model¹¹ of the Navier-Stokes equation for two viscous Newtonian immiscible fluids, with a variable surface tension coefficient.

Let’s consider a time dependent flow configuration of two incompressible viscous Newtonian fluids represented in Figure 1. The total domain contains two subspaces,${\Omega }_1$ for the fluid 1 and ${\Omega }_2$ for the fluid 2. The boundary of the fluid 1 is $\partial {\Omega }_1\cup {\Gamma }^{+}$ and the boundary for the fluid 2 is $\partial {\Omega }_2\cup {\Gamma }^{+}$ . The total domain is the union of domains $\Omega ={\Omega }_1\cup {\Omega }_2$ , the intersection ${\Omega }_1\cap {\Omega }_2=\varphi$ and the union of all external boundaries is $\partial \Omega =(\partial {\Omega }_1/{\Gamma }^{+})\cup (\partial {\Omega }_2/{\Gamma }^{-})$ .We assume that${\Omega }_1$ and ${\Omega }_2$ are connected but having this condition$\partial {\Omega }_1\cap \partial {\Omega }_2=\varphi$ .

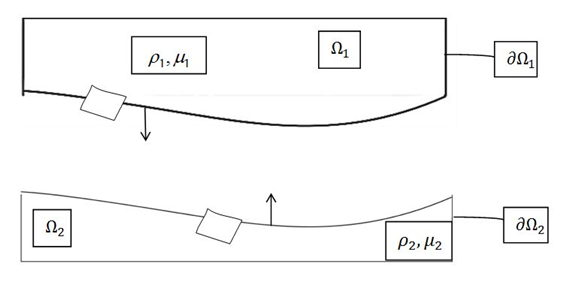
Figure 1 Two fluids model configuration space.

The physical properties for each domain are:

$\rho =\{\begin{array}{c}{\rho }_1 if x \in {\Omega }_1 \\ {\rho }_2 if x \in {\Omega }_2 \end{array}, \mu =\{\begin{array}{c}{\mu }_1 if x \in \Omega {}_1 \\ {\mu }_2 if x \in \Omega {}_2 \end{array}$ (1)

We are going to express the fundamental principles of dynamics for each control volume of fluid ${\Omega }_1$ , ${\Omega }_2$ and do a fusion between them through an interface ${\Gamma }^{*}$ ;(Figure 2).

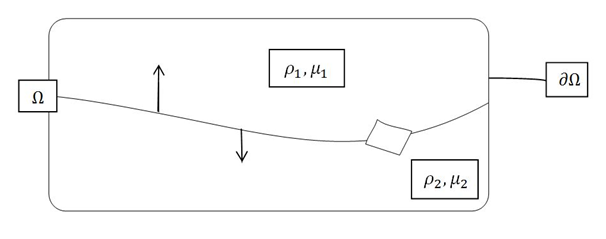
Figure 2 Fusion of two immiscible fluids through an interface.

Let $\overrightarrow{n}$ be the normal vector in each point of the external boundary in each domain${\Omega }_1$ and ${\Omega }_2$ . $\overrightarrow{n_1}$ the outside normal vector to each point of the interface ${\Gamma }^{+}$ and $\overrightarrow{n_2}$ the outside normal vector to each point of the interface${\Gamma }^{-}$ .

We distinguish two types of forces: Volumetric forces acting on the bulk of each fluid and surface forces acting on the boundary and the interface of separation between fluids.

For the fluid 1, we have:

${{\displaystyle \sum }}^{\text{}}Forces=\frac{D}{Dt}\underset{{\Omega }_1}{\overset{}{{\displaystyle \int }}}\left(\rho \overrightarrow{U}\right)d\Omega =\underset{{\Omega }_1}{\overset{}{{\displaystyle \int }}}\overrightarrow{F}d\Omega +\underset{\partial {\Omega }_1/{\Gamma }^{+}}{\overset{}{{\displaystyle \int }}}\overline{\overline{\sigma }}.\overrightarrow{n} d\Gamma +\underset{{\text{Γ}}^{+}}{\overset{}{{\displaystyle \int }}}\overline{\overline{\sigma }}.\overrightarrow{n_1} d\Gamma$ (2a)

For the fluid 2:

${{\displaystyle \sum }}^{\text{}}Forces=\frac{D}{Dt}\underset{{\Omega }_2}{\overset{}{{\displaystyle \int }}}\left(\rho \overrightarrow{U}\right)d\Omega =\underset{{\Omega }_2}{\overset{}{{\displaystyle \int }}}\overrightarrow{F}d\Omega +\underset{\partial {\Omega }_2/{\Gamma }^{+}}{\overset{}{{\displaystyle \int }}}\overline{\overline{\sigma }}.\overrightarrow{n} d\Gamma +\underset{{\text{Γ}}^{+}}{\overset{}{{\displaystyle \int }}}\overline{\overline{\sigma }}.\overrightarrow{n_2} d\Gamma$ (2b)

The addition of (2a)+ (2b)gives:

$\frac{D}{Dt}\underset{\Omega }{\overset{}{{\displaystyle \int }}}\left(\rho \overrightarrow{U}\right)d\Omega =\underset{\Omega }{\overset{}{{\displaystyle \int }}}\overrightarrow{F}d\Omega +\underset{\partial \Omega }{\overset{}{{\displaystyle \int }}}\overline{\overline{\sigma }}.\overrightarrow{n}d\Gamma +\underset{{\Gamma }^{+}}{\overset{}{{\displaystyle \int }}}\overline{\overline{\sigma }}.\overrightarrow{n_1}d\Gamma +\underset{{\Gamma }^{+}}{\overset{}{{\displaystyle \int }}}\overline{\overline{\sigma }}.\overrightarrow{n_2}d\Gamma$ (2c)

With $\Omega =\Omega {}_1\cup {\Omega }_2$ and$\partial \Omega =(\partial \Omega {}_1/{\Gamma }^{+})\cup \left(\partial \Omega {}_2/{\Gamma }^{-}\right)$

At the interface we have:

$\underset{{\Gamma }^{+}\to {\Gamma }^{*}}{Lim}\left(\underset{{\Gamma }^{+}}{\overset{}{{\displaystyle \int }}}\overline{\overline{\sigma }}.\overrightarrow{n_1}d\Gamma \right)=\underset{{\Gamma }^{*}}{\overset{}{{\displaystyle \int }}}\overline{\overline{({\sigma }_1}}).\overrightarrow{n}d\Gamma$ (3a)

$\underset{{\Gamma }^{+}\to {\Gamma }^{*}}{Lim}\left(\underset{{\Gamma }^{+}}{\overset{}{{\displaystyle \int }}}\overline{\overline{\sigma }}.\overrightarrow{n_2}d\Gamma \right)=\underset{\Gamma *}{\overset{}{{\displaystyle \int }}}\overline{\overline{({\sigma }_2}}).\overrightarrow{n}d\Gamma$ (3c)

With$\overrightarrow{n_1}=-\overrightarrow{n_2}=\overrightarrow{n}$

Finally, we obtain

$\frac{D}{Dt}\underset{\Omega }{\overset{}{{\displaystyle \int }}}\left(\rho \overrightarrow{U}\right)d\Omega =\underset{\Omega }{\overset{}{{\displaystyle \int }}}\overrightarrow{F}d\Omega +\underset{\partial \Omega }{\overset{}{{\displaystyle \int }}}\overline{\overline{\sigma }}.\overrightarrow{n}d\Gamma -\underset{\Gamma *}{\overset{}{{\displaystyle \int }}}\left({\overline{\overline{\sigma }}}_1-{\overline{\overline{\sigma }}}_2\right).\overrightarrow{n}d\Gamma$ (4)

Applying the divergence theorem to the integral of the external surface $\partial \Omega$ , we have

$\underset{\partial \Omega }{\overset{}{{\displaystyle \int }}}\overline{\overline{\sigma }}.\overrightarrow{n}d\Gamma =\underset{\Omega }{\overset{}{{\displaystyle \int }}}\nabla .\overline{\overline{\sigma }} d\Omega$ (5)

The last term of the equation (4) represent a difference between the stress tensors from each fluid, it’s a two-dimensional force. We introduce the Dirac function to express it in three dimensions. It represents the surface tension force between two fluids localized at the interface ${\overrightarrow{f}}_s\left(x,t\right)$ .

Finally, we have the one fluid model of the Navier-Stokes equation:

$\frac{\partial }{\partial t}\left(\rho \overrightarrow{U}\right)+\nabla .\left(\rho \overrightarrow{U}\right)-\overrightarrow{F}-\nabla .\overline{\overline{\sigma }}+{\overrightarrow{f}}_s\left(x,t\right)=0$ (6)

With ${\overrightarrow{f}}_s\left(x,t\right)=\left({\overline{\overline{\sigma }}}_1-{\overline{\overline{\sigma }}}_2\right).\overrightarrow{n}\delta \left(x\right)$ is the surface tension force at the interface of separation and  is the Dirac function¹² which is equal to the unity at the interface and equal to zero in the rest of the space (Bulk of fluid). The difference between values of stress tensors $\overline{\overline{\sigma }}$ on both sides of the interface in the expression term of${\overrightarrow{f}}_s\left(x,t\right)$ can be expressed with a jump operator $〚.〛$ :

$\left({\overline{\overline{\sigma }}}_1-{\overline{\overline{\sigma }}}_2\right).\overrightarrow{n}=〚\overline{\overline{\sigma }}\overrightarrow{.n_2}〛$ (7)

Equation (7) represent the jump condition over the interface of separation and it represent the surface tension force if we multiply it with the Dirac function to have a three dimensional force.

Let’s express the jump condition (equation 7) with physical and mathematical parameters. Let’s take an interface between two immiscible fluids $\Omega {}_{\text{1}}$ and $\Omega {}_{\text{2}}$ , S be a portion of this interface and C the closed contours of this portion. $\overrightarrow{n}$ , the normal vector to the interface and $\overrightarrow{t}$ the tangential from Figure 3.

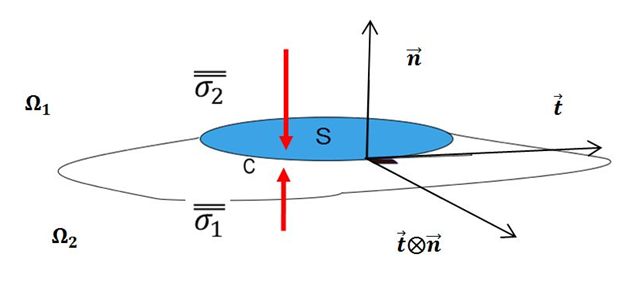
Figure 3 Forces acting on a surface of discontinuity

Forces acting at the interface between two immiscible fluids are composed from the force acting on the surface S and the force acting on the closed contour C of this surface. The mathematical translation of this physical phenomenon is:

$\overrightarrow{F}=\underset{A}{\overset{}{{\displaystyle \int }}}\left({\overline{\overline{\sigma }}}_1-{\overline{\overline{\sigma }}}_2\right).\overrightarrow{n}dA+\underset{\Gamma }{\overset{}{{\displaystyle \oint }}}\gamma \overrightarrow{t}\times \overrightarrow{n} d\Gamma$ (8)

With ${\overline{\overline{\sigma }}}_1$ and ${\overline{\overline{\sigma }}}_2$ the stress tensors on each fluid,$\gamma$ the superficial tension coefficient at the interface. Note that the volumetric forces are equal to zero at the interface because the volume of an interface is equal to zero. Even in absence of equilibrium the summation of all forces is equal to zero due to the fact that the interface doesn’t have a mass.

${{\displaystyle \sum }}^{\text{}}\overrightarrow{F}=m\overrightarrow{a}$ , with m=0.

Equation (8) will be:

$\underset{A}{\overset{}{{\displaystyle \int }}}\left({\overline{\overline{\sigma }}}_1-{\overline{\overline{\sigma }}}_2\right).\overrightarrow{n}dA+\underset{\text{Γ}}{\overset{}{{\displaystyle \oint }}}\gamma \overrightarrow{t}\times \overrightarrow{n} d\Gamma =0$ (9a)

$\underset{A}{\overset{}{{\displaystyle \int }}}\left({\overline{\overline{\sigma }}}_1-{\overline{\overline{\sigma }}}_2\right).\overrightarrow{n}dA=\underset{\Gamma }{\overset{}{{\displaystyle \oint }}}\gamma \overrightarrow{n}\times \overrightarrow{t} d\Gamma$ (9b)

$\underset{C}{\overset{}{{\displaystyle \oint }}}\overrightarrow{F}.\overrightarrow{t}dS=\underset{A}{\overset{}{{\displaystyle \int }}}\left(\overrightarrow{\nabla }\times \overrightarrow{F}\right).\overrightarrow{n}dA$

Applying the Stokes theorem to the right-hand side of the equation (9b):

$$\underset{C}{\overset{}{{\displaystyle \oint }}}\overrightarrow{F}.\overrightarrow{t}dS=\underset{A}{\overset{}{{\displaystyle \int }}}\left(\overrightarrow{\nabla }\times \overrightarrow{F}\right).\overrightarrow{n}dA$$

Considering $\overrightarrow{F}$ being the product of two vectors $\overrightarrow{F}=\overrightarrow{g}\times \overrightarrow{b}$ with $\overrightarrow{b}$ a constant vector, we obtain:

$\underset{C}{\overset{}{{\displaystyle \oint }}}\left(\overrightarrow{g}\times \overrightarrow{b}\right).\overrightarrow{t}dS=\underset{A}{\overset{}{{\displaystyle \int }}}\left(\overrightarrow{\nabla }\times \left(\overrightarrow{g}\times \overrightarrow{b}\right)\right).\overrightarrow{n}dA$

We have $\overrightarrow{\nabla }\times \left(\overrightarrow{g}\times \overrightarrow{b}\right)=\left(\overrightarrow{\nabla }.\overrightarrow{b}\right)\overrightarrow{g}-\left(\overrightarrow{\nabla }.\overrightarrow{g}\right)\overrightarrow{b}+\overrightarrow{b}.\left(\overrightarrow{\nabla } \overrightarrow{g}\right)-\overrightarrow{g}.\left(\overrightarrow{\nabla } \overrightarrow{b}\right)$

But$\left(\overrightarrow{\nabla }.\overrightarrow{b}\right)=\left(\overrightarrow{\nabla } \overrightarrow{b}\right)=0$

So, the last expression become$\overrightarrow{\nabla }\times \left(\overrightarrow{g}\times \overrightarrow{b}\right)=-\left(\overrightarrow{\nabla }.\overrightarrow{g}\right)\overrightarrow{b}+\overrightarrow{b}.\left(\overrightarrow{\nabla } \overrightarrow{g}\right)$

We obtain $\underset{C}{\overset{}{{\displaystyle \oint }}}\left(\overrightarrow{g}\times \overrightarrow{b}\right).\overrightarrow{t}dS=\underset{A}{\overset{}{{\displaystyle \int }}}\left(-\left(\overrightarrow{\nabla }.\overrightarrow{g}\right)\overrightarrow{b}+\overrightarrow{b}.\left(\overrightarrow{\nabla } \overrightarrow{g}\right)\right).\overrightarrow{n} dA$

With taking $\overrightarrow{g}=\gamma \overrightarrow{n}$ :

$\underset{C}{\overset{}{{\displaystyle \oint }}}\left(\gamma \overrightarrow{n}\times \overrightarrow{b}\right).\overrightarrow{t}dS=\underset{A}{\overset{}{{\displaystyle \int }}}\left(\left(-\overrightarrow{\nabla }.\left(\gamma \overrightarrow{n}\right)\right)\overrightarrow{b}+\overrightarrow{b}.\left(\overrightarrow{\nabla } \left(\gamma \overrightarrow{n}\right)\right)\right).\overrightarrow{n}dA$ $\underset{C}{\overset{}{{\displaystyle \oint }}}\gamma \left(\overrightarrow{t}\times \overrightarrow{n}\right)dS=\underset{A}{\overset{}{{\displaystyle \int }}}\left(-\overrightarrow{\nabla }.\left(\gamma \overrightarrow{n}\right)\overrightarrow{n}+\left(\overrightarrow{\nabla } \left(\gamma \overrightarrow{n}\right)\right).\overrightarrow{n}\right)dA$ $\overrightarrow{\nabla }.\left(\gamma \overrightarrow{n}\right)=\overrightarrow{\nabla }\gamma .\overrightarrow{n}+\gamma \overrightarrow{\nabla }.\overrightarrow{n}$ $\underset{C}{\overset{}{{\displaystyle \oint }}}\gamma \left(\overrightarrow{t}\times \overrightarrow{n}\right)dS=\underset{A}{\overset{}{{\displaystyle \int }}}[-\left(\overrightarrow{\nabla }\gamma .\overrightarrow{n}\right)\overrightarrow{n}-\gamma \left(\overrightarrow{\nabla }.\overrightarrow{n} \right)\overrightarrow{n}+\left(\overrightarrow{\nabla }\gamma \otimes \overrightarrow{n}\right).\overrightarrow{n}]dA$ (10)

By definition Mansour et al.¹³:$-\overrightarrow{\nabla }.\overrightarrow{n}=\kappa$

$\kappa$ represent the curvature of the interface

$\left(\overrightarrow{\nabla }\gamma \otimes \overrightarrow{n}\right).\overrightarrow{n}=\overrightarrow{\nabla }\gamma \left(\overrightarrow{n} .\overrightarrow{n}\right)=\overrightarrow{\nabla }\gamma$

Considering the divergence operator been the summation of the normal component and the tangential one, we have:

$\begin{array}{l}\overrightarrow{\nabla }\gamma =\overrightarrow{{\nabla }_N}\gamma +\overrightarrow{{\nabla }_{\Gamma }}\gamma \\ \overrightarrow{{\nabla }_{\Gamma }}\gamma =\overrightarrow{\nabla }\gamma -\overrightarrow{n}\otimes \overrightarrow{n}\left(\overrightarrow{\nabla }\gamma \right)\\ \overrightarrow{{\nabla }_{\Gamma }}\gamma =\left(\parallel -\overrightarrow{n}\otimes \overrightarrow{n}\right)\left(\overrightarrow{\nabla }\gamma \right)\end{array}$

With $\left(\parallel -\overrightarrow{n}\otimes \overrightarrow{n}\right)$ represent the projector of the delta operator at the interface.

Equation (10) becomes:

$\underset{C}{\overset{}{{\displaystyle \oint }}}\gamma \left(\overrightarrow{t}\times \overrightarrow{n}\right)dS=\underset{A}{\overset{}{{\displaystyle \int }}}[\gamma \text{κ}\overrightarrow{n}-\left(\overrightarrow{\nabla }\gamma \right)+\left(\overrightarrow{\nabla }\gamma \otimes \overrightarrow{n}\right).\overrightarrow{n}]dA$ $\underset{C}{\overset{}{{\displaystyle \oint }}}\gamma \left(\overrightarrow{t}\times \overrightarrow{n}\right)dS=\underset{A}{\overset{}{{\displaystyle \int }}}[\gamma \kappa \overrightarrow{n}-\left(\overrightarrow{{\nabla }_{\Gamma }}\gamma \right)]dA$ $\underset{A}{\overset{}{{\displaystyle \int }}}\left({\overline{\overline{\sigma }}}_1-{\overline{\overline{\sigma }}}_2\right).\overrightarrow{n}dA=-\underset{A}{\overset{}{{\displaystyle \int }}}[\gamma \kappa \overrightarrow{n}-\left(\overrightarrow{{\nabla }_{\Gamma }}\gamma \right)]dA$ $\underset{A}{\overset{}{{\displaystyle \int }}}\left({\overline{\overline{\sigma }}}_1-{\overline{\overline{\sigma }}}_2\right).\overrightarrow{n}dA+\underset{A}{\overset{}{{\displaystyle \int }}}[\gamma \kappa \overrightarrow{n}-\left(\overrightarrow{{\nabla }_{\Gamma }}\gamma \right)]dA=0$ $〚\overline{\overline{\sigma }}\overrightarrow{.n}〛 =\left[-\gamma \kappa \overrightarrow{n}+\left(\overrightarrow{{\nabla }_{\Gamma }}\gamma \right)\right]$ (11)

Equation (11) represents the jump condition at an interface between two immiscible fluids with a variable surface tension coefficient.

The jump condition have a dimension of a force, it seems that the deformation of the interface is a consequence of balance forces acting on fluids or an energy balance during the evolution .The second term of this condition correspond to a surface gradient of the surface tension coefficient $\gamma ,\overrightarrow{{\nabla }_{\Gamma }}=\left(1-\overrightarrow{n}\otimes \overrightarrow{n}\right)\overrightarrow{\nabla }$ is a projection of $\overrightarrow{\nabla }$ on the oriented surface .This term translate the Marangoni effect.

In the case of stratified flow $\kappa \text{=0}$ , the fluid can’t be static until$\overrightarrow{{\nabla }_{\Gamma }}\gamma =0$ .In other case the flow is going to be driven by the surface gradient which represent the Marangoni effect.

The Marangoni effect is only possible if the superficial tension between two points of the interface is different. It suggest the fact that in absence of initial velocity for a fluid, his motion can be driven by the Marangoni effect, in this case the flow direction will be from the point where the surface tension coefficient is low to the point of high surface tension coefficient$\overrightarrow{{\nabla }_{\Gamma }}\gamma =0$ .

We implement the following numerical example of Navier-Stokes two phase flow problem. We used the XFEM¹⁴ for the discretization of velocity and pressure. The program was implemented in the computational FEniCS platform.¹⁵

In this example we are going to consider two immiscible fluids (air/ water) with an interface of separation where the superficial tension $\gamma$ is not constant. The two immiscible fluids are without initial velocity for both. It means that the both phases are statics at t=0s.

For the half of the configuration${\gamma }_1={70.10}^{-3}N.m^{-1}$ and for the other half ${\gamma }_2={72.10}^{-3}N.m^{-1}$

As we can see Figure 4, there is a displacement of the fluid from a side to another because of the difference between the coefficients of superficial tension.

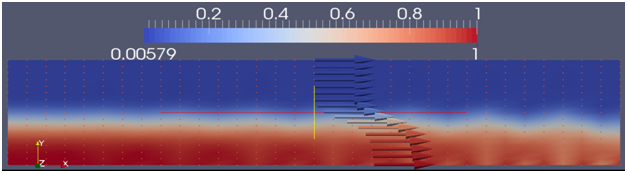
Figure 4 Displacement effects of fluids due to the Marangoni effect at the interface.

As we saw it in the equation (11) the jump at the interface is:

$〚\overline{\overline{\sigma }}\overrightarrow{.n}〛 =\left[-\gamma \kappa \overrightarrow{n}+\left(\overrightarrow{{\nabla }_{\Gamma }}\gamma \right)\right]$

In our example we have a stratified flow, the interface is straight, so the curvature is equal to zero $\kappa \text{=0}$ .The only term stays is the interfacial gradient of the coefficient of superficial tension

$〚\overline{\overline{\sigma }}\overrightarrow{.n}〛 =\left(\overrightarrow{{\nabla }_{\Gamma }}\gamma \right)$

We can clearly see from this result that the movement of the interface is a result of non-zero gradient of the superficial tension, it’s the Marangoni effect.

The movement of the interface is in the positive gradient direction, it’s from the smaller coefficient of superficial tension to the bigger one.

This study gives an analytical detailed description of the Marangoni phenomenon with mathematical and physical parameters responsible for this .With this work we have the confirmation that the Marangoni effect is very important when we study two phase flow problems. The impact of this phenomenon is so important that it could be a reason for the displacement of fluids in the absence of initial velocity. In the case where we have a dynamic system, it’s a big factor to create instabilities and interfacial turbulence.

None.

Authors declare there is no conflict of interest in publishing the article.

1. Ding Zijing, Rong Liu, Teck Neng Wong, et al. Absolute instability induced by Marangoni effect in thin liquid film flows on vertical cylindrical surfaces. Chemical Engineering Science. 2018;177:261−269.
2. Pariona Moises Meza, André Felipe Taques, Luciano Allan Woiciechowski. The Marangoni effect on microstructure properties and morphology of laser-treated Al-Fe alloy with single track by FEM: Varying the laser beam velocity. International Journal of Heat and Mass Transfer. 2018;119:10−19.
3. Pawar Y, Stebe KJ. Marangoni effects on drop deformation in an extensional flow: The role of surfactant physical chemistry. I. Insoluble surfactants. Physics of Fluids. 1996;8(7):1738−1751.
4. Stone HA, Stroock AD, Ajdari A. Engineering flows in small devices: microfluidics toward a lab−on−a−chip. Annu. Rev Fluid Mech. 2004;36:381−411.
5. Park J, Moon J. Control of colloidal particle deposit patterns within Pico liter droplets ejected by ink-jet printing. Langmuir. 2006;22(8):3506−3513.
6. Mishra S, Barton KL, Alleyne AG, et al. High-speed and drop-on-demand printing with a pulsed electrohydrodynamic jet. Journal of Micromechanics and Microengineering. 2010;20(9):095026.
7. Talbot EL, Yow HN, Yang L, et al. Printing small dots from large drops. ACS Appl Mater Interfaces. 2015;7(6), 3782−3790.
8. Kong YL, Tamargo IA, Kim H, et al. 3D printed quantum dot light-emitting diodes. Nano letters. 2014;14(2):7017−7023.
9. Kuang M, Wang L, Song Y. Controllable printing droplets for high‐resolution patterns. Advanced materials. 2014;26(40): 6950−6958.
10. Shmuylovich L, Shen AQ, Stone HA. Surface morphology of drying latex films: multiple ring formation. Langmuir, 2002;18(9):3441−3445.
11. Brackbill JU, Douglas B Kothe, Charles Zemach. A continuum method for modeling surface tension. Journal of computational physics. 1992;100(2):335−354.
12. Spiegel MR. The Dirac Delta‐Function and the Summation of Fourier series. Journal of Applied Physics. 1952;23(8):906−909.
13. Mansour Nagi N, Thomas S Lundgren. Satellite formation in capillary jet breakup. Physics of Fluids A: Fluid Dynamics. 1990;2(7):1141−1144.
14. Sauerland H, Fries TP. The stable XFEM for two-phase flows. Computers & Fluids. 2013;87:41−49.
15. Logg A, Mardal KA, Wells G. Automated solution of differential equations by the finite element method: The FEniCS book. Vol. 84, Springer-Verlag Berlin Heidelberg, Germany; 2012, p.731.