The thermal instability of Walters B′ viscoelastic fluid in the presence of uniform horizontal magnetic field and suspended particles through porous medium is considered. It is found that Walters B′ viscoelastic fluid behaves like a Newtonian fluid for stationary convection. Further, the medium permeability and suspended particles hasten the onset of convection whereas the magnetic field postpones the onset of convection, for the case of stationary convection. A sufficient condition for the invalidity of the ‘Principle of exchange of stabilities’ is derived, in the context, which states that the exchange principle is not valid provided the thermal Rayleigh number $R$ , medium permeability $P_l$ and suspended particles parameter $H^{\prime }$ are restricted by the inequality $\frac{H^{\prime }{P}_{l}R}{{\pi }^2}<1$ . Further it is found that the magnetic field and viscoelasticity introduce oscillatory modes in the system which was non-existent in their absence.

Keywords: Walters B′viscoelastic fluid; Thermal instability; Suspended particles; Uniform horizontal magnetic field; Porous medium; Rayleigh number; Prandtl number; Darcys law

A detailed account of the theoretical and experimental study of thermal instability (Bénard convection) in Newtonian fluids, under varying assumptions of hydrodynamics and hydromagnetics, has been treated in detail by Chandrasekhar.¹ The use of Boussinesq approximation has been made throughout, which states that the density may be treated as a constant in all the terms in the equations of motion except the external force term. Chandra² observed that in an air layer, convection occurred at much lower gradients than predicted if the layer depth was less than 7mm, and called this motion “Columnar instability”. However, a Bénard -type cellular convection was observed for layers deeper than 10mm. Chandra² added an aerosol to mark the flow pattern. Thus there is a decades-old contradiction between the theory and the experiment. Scanlon et al.,³ have considered the effect of suspended particles on the onset of Bénard convection and found that the critical Rayleigh number was reduced solely because the heat capacity of the pure fluid was supplemented by that of the particles. The effect of suspended particles was thus found to destabilize the layer. Palaniswamy et al.,⁴ have considered the stability of shear flow of stratified fluids with fine dust and have found the effect of fine dust to increase the region of instability. The medium has been considered to be non-porous and the fluid to be Newtonian in all the above studies.

Lapwood⁵ has studied the stability of convective flow in a porous medium using Rayleigh’s procedure. Wooding⁶ has considered the Rayleigh instability of a thermal boundary layer in flow through porous medium. The gross effect when the fluid slowly percolates through the pores of the rock is represented by the well known Darcy’s law. The problem of thermal instability in fluids in a porous medium is of importance in geophysics, soil sciences, ground water hydrology and astrophysics. The development of geothermal power resources has increased general interest, in the properties of convection in porous media. The effect of a magnetic field on the stability of such a flow is of interest in geophysics, particularly in the study of Earth’s core where the Earth’s mantle, which consists of conducting fluid, behaves like a porous medium which can become convectively unstable as a result of differential diffusion. The other application of the results of flow through a porous medium in the presence of a magnetic field is in the study of the stability of a convective flow in the geothermal region.

The importance of non-Newtonian fluids in modern technology and industries is ever increasing and the investigations on such fluids are desirable. One such class of non-Newtonian fluids is Walters B¢ fluid. Chakraborty et al.,⁷ have studied the flow of unsteady viscoelastic (Walters B¢ liquid) conducting fluid through two porous concentric non-conducting infinite circular cylinders rotating with different angular velocities in the presence of uniform axial magnetic field. Sharma et al.,⁸ have studied the stability of two superposed Walters B¢ viscoelastic liquids. In another study, Sharma et al.,⁹ have studied the Rayleigh-Taylor instability of two superposed conducting Walters B¢ elastico-viscous fluids in hydromagnetics. Kumar¹⁰ has studied the stability of two superposed viscoelastic (Walters B¢) fluid-particle mixtures in porous medium. MHD flow of viscoelastic (Walters liquid model B') fluid through porous medium with heat source has been considered by Bhagwat et al.¹¹ Attia et al.,¹² have studied the stability of flow through a porous medium of a viscoelastic fluid above a stretching plate. Magneto-gravitational instability of a Walters B' viscoelastic rotating anisotropic heat-conducting fluid in Brinkman porous medium has been considered by Sayed et al.¹³

In many geophysical fluid dynamical problems encountered, the fluid is electrically conducting and a uniform magnetic field of the Earth pervades the system. A study has, therefore, been made to study the effect of suspended (or dust) particles on the Walters B¢ viscoelastic fluid heated from below in porous medium in the presence of a uniform horizontal magnetic field. The problem is often encountered in chemical engineering, paper and pulp technology and several geophysical situations.

Here we consider an infinite horizontal layer of an electrically conducting Walters B′ viscoelastic fluid permeated with suspended (dust) particles and bounded by the planes z = 0 and z = d in a porous medium. This layer is heated from below so that, the temperatures and densities at the bottom surface z = 0 are T0 and r0 and at the upper surface z = d are T_d and ${\rho }_d$ respectively and that a uniform temperature gradient $\beta \left(=\left|\frac{dT}{dz}\right|\right)$ is maintained. A uniform horizontal magnetic field $\overrightarrow{H}\left(H,0,0\right)$ and gravity field $\overrightarrow{g}\left(0,0,-g\right)$ pervades the system.

The equations of motion and continuity for Walters B′ viscoelastic fluid in the presence of suspended particles and magnetic field in porous medium are

$\begin{array}{l}\frac{1}{\in }\left[\frac{\partial \overrightarrow{q}}{\partial t}+\frac{1}{\in }\left(\overrightarrow{q}\cdot \nabla \right)\overrightarrow{q}\right]=-\frac{1}{{\rho }_0}\nabla p-g\left(1+\frac{\delta \rho }{{\rho }_0}\right)\overrightarrow{\lambda }-\frac{1}{k_1}\left(\upsilon -{\upsilon }^{\prime }\frac{\partial }{\partial t}\right)\overrightarrow{q}\\ +\frac{KN}{{\rho }_0\in }\left({\overrightarrow{q}}_d-\overrightarrow{q}\right)+\frac{{\mu }_e}{4\pi {\rho }_0}\left(\nabla \times \overrightarrow{H}\right)\times \overrightarrow{H}\end{array}$ ,            (1)

$\nabla \cdot \overrightarrow{q}=0,$ (2)

where $p,\rho ,T,\overrightarrow{q}\left(u,v,w\right),{\overrightarrow{q}}_d\left(\overline{x},t\right),N\left(\overline{x},t\right),\upsilon$ and ${\upsilon }^{\prime }$ denote fluid pressure, density, temperature, filter velocity, suspended particles velocity, suspended particles number density, kinematic viscosity and kinematic viscoelasticity respectively. Symbol $\text{'}\in \text{'}$ is the medium porosity, k₁ is the medium permeability, g is the acceleration due to gravity, $\overline{x}=\left(x,y,z\right),\overrightarrow{\lambda }=\left(0,0,1\right)$ and $K=6\pi \mu {\eta }^{\prime },{\eta }^{\prime }$ , being the particle radius, is the Stokes’ drag coefficient. Assuming a uniform particle size, a spherical shape and small relative velocities between the fluid and particles, the presence of particles adds an extra force term in the equations of motion (1), proportional to the velocity difference between the particles and the fluid.

Since the force exerted by the fluid on the particles is equal and opposite to that exerted by the particles on the fluid, there must be an extra force term, equal in magnitude but opposite in sign, in the equations of motion for the particles. Interparticle reactions are ignored because the distances between the particles are assumed to be quite large compared with their diameter. The effects due to pressure, gravity, Darcy’s force and magnetic field on the particles are small and so are ignored. If mN is the mass of particles per unit volume, then the equations of motion and continuity for the particles, under the above assumptions, are

$mN\left[\frac{\partial {\overrightarrow{q}}_d}{\partial t}+\frac{1}{\in }\left({\overrightarrow{q}}_d\cdot \nabla \right){\overrightarrow{q}}_d\right]=KN\left(\overrightarrow{q}-\overrightarrow{q}{}_d\right),$ (3)

$\in \frac{\partial N}{\partial t}+\nabla \cdot \left(N{\overrightarrow{q}}_d\right)=0.$ (4)

If C_v, C_pt, T and $q^{\prime }$ denote the heat capacity of fluid at constant volume, heat capacity of the particles, temperature and ‘effective thermal conductivity’ of the pure fluid, respectively. Assuming that the particles and the fluid are in thermal equilibrium, the equation of heat conduction gives

$\left[{\rho }_0{C}_v\in +{\rho }_s{C}_s\left(1-\in \right)\right]\frac{\partial T}{\partial t}+{\rho }_0{C}_v\left(\overrightarrow{q}\cdot \nabla \right)T+mN{C}_{pt}\left(\in \frac{\partial }{\partial t}+{\overrightarrow{q}}_d\cdot \nabla \right)T=q^{\prime }{\nabla }^{2}T,$ (5)

where ${\rho }_s,C_s$ are the density and the heat capacity of the solid (porous matrix) material respectively.

The Maxwell’s equations yield

$\in \frac{\partial \overrightarrow{H}}{\partial t}=\left(\overrightarrow{H}\cdot \nabla \right)\overrightarrow{q}+\in \eta {\nabla }^2\overrightarrow{H}$ ,                              (6)

$\nabla \cdot \overrightarrow{H}=0$ ,                                                              (7)

where $\eta$ stands for the electrical resistivity.

The equation of state for the fluid is

$\rho ={\rho }_0\left[1-\alpha \left(T-T_0\right)\right]$ ,                     (8)

where $\alpha$ is the coefficient of thermal expansion and the suffix zero refers to values at the reference level z = 0. The kinematic viscosity $\nu$ , kinematic viscoelasticity ${\nu }^{\prime }$ , magnetic permeability ${\mu }_e$ , electrical resistivity $\eta$ and coefficient of thermal expansion $\alpha$ are all assumed to be constants.

The basic motionless solution is

$\overrightarrow{q}=(0,0,0),{\overrightarrow{q}}_d=(0,0,0),T=T_0-\beta z,\rho ={\rho }_0(1+\alpha \beta z),N=N_0,$ a constant.        (9)

Assume small perturbations around the basic solution and let $\delta p,\delta \rho ,\theta ,\overrightarrow{q}\left(u,v,w\right),{\overrightarrow{q}}_d\left(l,r,s\right),N$ and $\overrightarrow{h}\left(h_x,h_y,h_z\right)$ denote respectively the perturbations in fluid pressure p, density $\rho$ , temperature T, fluid velocity (0, 0, 0), suspended particles velocity (0, 0, 0), suspended particles number density N₀ and magnetic. T field $\overrightarrow{H}\left(H,0,0\right)$ he change in density δρ caused mainly by the perturbation θ in temperature, is given by

$\delta \rho =-\alpha {\rho }_0\theta$ .                         (10)

Then the linearized perturbed equations of Walters B′ viscoelastic fluid become

$\begin{array}{l}\frac{1}{\in }\frac{\partial \overrightarrow{q}}{\partial t}=-\frac{1}{{\rho }_0}\nabla \delta p+g\alpha \theta \overrightarrow{\lambda }-\frac{1}{k_1}\left(\upsilon -{\upsilon }^{\prime }\frac{\partial }{\partial t}\right)\overrightarrow{q}+\frac{K{N}_0}{{\rho }_0\in }\left({\overrightarrow{q}}_d-\overrightarrow{q}\right)\\ +\frac{{\mu }_e}{4\pi {\rho }_0}\left(\nabla \times \overrightarrow{h}\right)\times \overrightarrow{H}\end{array}$ ,      (11)

$\nabla \cdot \overrightarrow{q}=0$ ,                              (12)

$m{N}_0\frac{\partial {\overrightarrow{q}}_d}{\partial t}=K{N}_0\left(\overrightarrow{q}-{\overrightarrow{q}}_d\right)$ ,                                  (13)

$\left(E+h\in \right)\frac{\partial \theta }{\partial t}=\beta \left(w+hs\right)+\kappa {\nabla }^2\theta$ ,                   (14)

$\in \frac{\partial \overrightarrow{h}}{\partial t}=\left(\overrightarrow{H}\cdot \nabla \right)\overrightarrow{q}+\in \eta {\nabla }^2\overrightarrow{h}$ ,                                                (15)

$\nabla \cdot \overrightarrow{h}=0$ ,                                                               (16)

where $E=\in +\left(1-\in \right)\frac{{\rho }_s{C}_s}{{\rho }_0{C}_v},h=\frac{m{N}_0{C}_{pt}}{{\rho }_0{C}_v}$ and $\kappa =\frac{q^{\prime }}{{\rho }_0{C}_v}$ .

Eliminating ${\overrightarrow{q}}_d$ in equation (11) with the help of equation (13), writing the scalar components of resulting equation and eliminating u, v, h_x, h_y, $\delta p$ between them, by using equation (12) and equation (16), we obtain

$\begin{array}{l}{n}^{\prime }\left({\nabla }^{2}w\right)+\frac{\in }{k_1}\left(\upsilon -{\upsilon }^{\prime }\frac{\partial }{\partial t}\right){\nabla }^{2}w-\in g\alpha \left(\frac{{\partial }^2\theta }{\partial x^2}+\frac{{\partial }^2\theta }{\partial y^2}\right)\\ -\frac{{\mu }_e\in H}{4\pi {\rho }_0}\frac{\partial }{\partial x}\left({\nabla }^2{h}_z\right)=0\end{array}$ ,                    (17)

$\left(\frac{m}{K}\frac{\partial }{\partial t}+1\right)\left[\overline{E+h\in }\frac{\partial }{\partial t}-\kappa {\nabla }^2\right]\theta =\beta \left[\frac{m}{K}\frac{\partial }{\partial t}+1+h\right]w,$ (18)

$\in \left[\frac{\partial }{\partial t}-\eta {\nabla }^2\right]h_z=H\frac{\partial w}{\partial x}$ ,                                                                   (19)

where $n^{\prime }=\frac{\partial }{\partial t}\left[1+\frac{m{N}_{0}K|{\rho }_0}{m\frac{\partial }{\partial t}+K}\right]$ .

Here we analyze the disturbances into normal modes and assume that the perturbation quantities are of the form

$\left[w,\theta ,h_z\right]=\left[W\left(z\right),\Theta \left(z\right),X\left(z\right)\right]\exp \left(i{k}_{x}x+i{k}_{y}y+nt\right),$ (20)

where k_x, k_y are wave numbers along the x- and y-directions respectively. $k=\sqrt{k_x^2+k_y^2}$ is the resultant wave number and n is, in general , a complex constant. Using expression (20), equations (17)-(19) in non-dimensional form become

$\left[\frac{{\sigma }^{\prime }}{\in }+\frac{1}{P_{\mathcal{l}}}\left\{1-F\sigma \right\}\right]\left(D^2-a^2\right)W+\frac{g\alpha d^2{a}^2\Theta }{\upsilon }-\frac{i{k}_x{\mu }_{e}H{d}^2}{4\pi {\rho }_0\upsilon }\left(D^2-a^2\right)X=0$ ,               (21)

$\left[\frac{\tau \upsilon \sigma }{d^2}+1\right]\left[D^2-a^2-\overline{E+h\in }{p}_1\sigma \right]\Theta =-\frac{\beta d^2}{\kappa }\left[H^{\prime }+\frac{\tau \upsilon \sigma }{d^2}\right]W,$ (22)

$\left[D^2-a^2-p_2\sigma \right]X=-\frac{i{k}_{x}H{d}^2}{\in \eta }W,$ (23)

where we have expressed the coordinates x, y, z in the new unit of length d, time t in the new unit of length $\frac{d^2}{\kappa }$ and put a = kd, $\sigma =\frac{n{d}^2}{\upsilon },p_1=\frac{\upsilon }{\kappa }$ is the Prandtl number, $p_2=\frac{\upsilon }{\eta }$ is the magnetic Prandtl number, ${\rho }_l=\frac{k_1}{d^2}$ is the dimensionless medium permeability, $F=\frac{{\upsilon }^{\prime }}{d^2}$ is the dimensionless kinematic viscoelasticity, ${\sigma }^{\prime }=\frac{n^{\prime }{d}^2}{\upsilon }$ , $H^{\prime }=h+1,\tau =\frac{m\xi }{\kappa d^2}$ and $D=\frac{d}{dz}$ .

Eliminating $\Theta$ and X between equations (21) - (23), we obtain

$\begin{array}{l}\left[1+\frac{\upsilon \tau \sigma }{d^2}\right]\left[D^2-a^2-\overline{E+h\in }{p}_1\sigma \right][\left\{\frac{{\sigma }^{\prime }}{\in }+\frac{1}{P_{\mathcal{l}}}\left(1-F\sigma \right)\right\}\left(D^2-a^2-p_2\sigma \right)\\ -\frac{k_x^{2}Q}{\in }]\left(D^2-a^2\right)W=R{a}^2\left[H^{\prime }+\frac{\upsilon \tau \sigma }{d^2}\right]\left[D^2-a^2-p_2\sigma \right]W,\end{array}$ (24)

where $R=\frac{g\alpha \beta d^4}{\upsilon \kappa }$ is the Rayleigh number and $Q=\frac{{\mu }_e{H}^2{d}^2}{4\pi {\rho }_0\upsilon \eta }$ is the Chandrasekhar¹ number.

Here we consider the case in which both the boundaries are free, the medium adjoining the fluid is perfectly conducting and temperatures at the boundaries are kept fixed. The case of two free boundaries is little artificial but allows us to have analytical solution. The boundary conditions, appropriate to the problem, are Chandrasekhar S.¹

$W=0,D^{2}W=0,\Theta =0,X=0$ at z = 0 and z = 1 . (25)

Using the above boundary conditions (25), it can be shown with the help of equations (21) - (23) that all the even order derivatives of W must vanish for z = 0 and z = 1 and hence the proper solution of W characterizing the lowest mode is

$W=W_0\sin \pi z$ ,                                     (26)

where W₀ is a constant.

Substituting the proper solution (26) in equation (24), we obtain the dispersion relation

$R_1=\frac{\begin{array}{l}\left(1+x\right)\left(1+x+\overline{E+h\in }i{\sigma }_1{p}_1\right)\left(1+\frac{i\upsilon \tau {\pi }^2{\sigma }_1}{d^2}\right)[\frac{i{{\sigma }^{\prime }}_1}{\in }+\\ +\frac{1}{P}\left\{1-i{\pi }^{2}F{\sigma }_1\right\}\left\{1+x+i{\sigma }_1{p}_2\right\}+\frac{Q_{1}x{\cos }^2\theta }{\in }]\end{array}}{x\left[H^{\prime }+\frac{i\upsilon \tau {\pi }^2{\sigma }_1}{d^2}\right]\left[1+x+i{\sigma }_1{p}_2\right]}$ ,                            (27)

where $x=\frac{a^2}{{\pi }^2},i{\sigma }_1=\frac{\sigma }{{\pi }^2},P={\pi }^2{P}_{\mathcal{l}},R_1=\frac{R}{{\pi }^4},i{{\sigma }^{\prime }}_1=\frac{{\sigma }^{\prime }}{{\pi }^2},Q_1=\frac{Q}{{\pi }^2}$ and $k_x=k\cos \theta$ .

When the instability sets in as stationary convection, the marginal state will be characterized by $\sigma =0$ . Putting $\sigma =0$ , the dispersion relation (27) reduces to

$R_1=\frac{\left(1+x^{}\right)\left[\frac{1+x}{P}+\frac{Q_{1}x{\cos }^2\theta }{\in }\right]}{x{H}^{\prime }}$ .                                   (28)

We thus find that for stationary convection the viscoelastic parameter F vanishes with σ and Walters B′ viscoelastic fluid behaves like an ordinary Newtonian fluid.

To study the effects of magnetic field, suspended particles and medium permeability, we examine the natures of $\frac{d{R}_1}{d{Q}_1},\frac{d{R}_1}{d{H}^{\prime }}$ and $\frac{d{R}_1}{dP}$ . Equation (28) yields

$\frac{d{R}_1}{d{Q}_1}=\frac{\left(1+x\right){\cos }^2\theta }{H^{\prime }\in }$ ,                                          (29)

$\frac{d{R}_1}{d{H}^{\prime }}=-\frac{\left(1+x\right)\left[\frac{1+x}{P}+\frac{Q_{1}x{\cos }^2\theta }{\in }\right]}{x{H^{\prime }}^2}$ ,             (30)

$\frac{d{R}_1}{dP}=-\frac{{\left(1+x\right)}^2}{x{H}^{\prime }{P}^2}$ .                                                (31)

It is clear from equations (29)-(31) that for stationary convection the magnetic field postpone the onset of convection whereas the suspended particles and medium permeability hasten the onset of convection in Walters B′ viscoelastic fluid permeated with suspended particles, heated from below in porous medium in presence of a uniform horizontal magnetic field.

Graphs have been plotted between R1 and x for various values of Q₁, P and $H^{\prime }$ . It is evident from Figures 1-3 that the magnetic field postpones the onset of convection while medium permeability and suspended particles hasten the onset of convection.

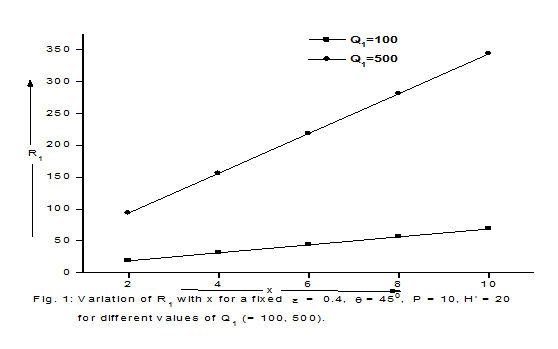
Figure 1 Variation of R₁ with X for a fixed $\in =0.4,\theta ={45}^{\circ },P=10,H^{\prime }=20$ for different values of Q₁ (=100,500).

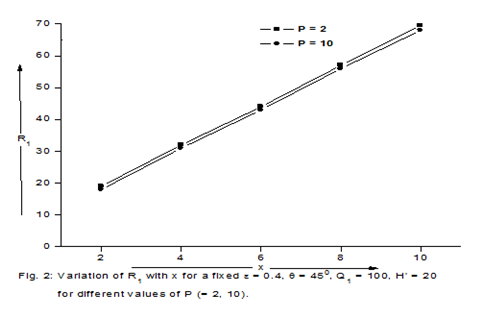
Figure 2 Variation of R₁ with X for a fixed $\in =0.4,\theta ={45}^{\circ },Q_1=100,H^{\prime }=20$ for different values of P (=2, 10).

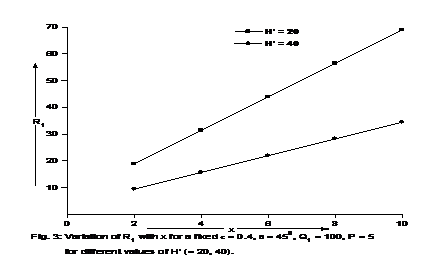
Figure 3 Variation of R₁ with X for a fixed $\in =0.4,\theta ={45}^{\circ },Q_1=100,P=5$ for different values of $H^{\prime }(=20,40)$ .

We first prove the following lemma:
Lemma: If $\left[\sigma ={\sigma }_r+i{\sigma }_i,W,\Theta ,X\right]$ is a non-trivial solution of the double Eigen value problem for ${\sigma }_{r}and{\sigma }_i$ described by the equations (21)-(23) with the boundary conditions (25). Then a necessary condition for $\sigma =0\left(i.e.{\sigma }_r={\sigma }_i=0\right)$ to be an Eigen value is that

${\displaystyle \underset{0}{\overset{1}{\int }}\left({\left|D\Theta \right|}^2+a^2{\left|\Theta \right|}^2\right)dz\le \frac{{\beta }^2{d}^4{H^{\prime }}^2}{{\kappa }^2{\pi }^2}{\displaystyle \underset{0}{\overset{1}{\int }}{\left|W\right|}^{2}dz.}}$

Proof of Lemma: Since $\sigma =0$ is an Eigen value, we have from equation (22)

$\left(D^2-a^2\right)\Theta =-\frac{\beta d^2{H}^{\prime }}{\kappa }W.$ (32)

Multiplying both sides of equation (32) by ${\Theta }^{*}$ (the complex conjugate of $\Theta$ ), integrating the resulting equation by parts for sufficient number of times over the vertical range of z by making the use of boundary conditions (25) and separating the real parts of both sides of the equation so obtained, we get

${\displaystyle \underset{0}{\overset{1}{\int }}\left({\left|D\Theta \right|}^2+a^2{\left|\Theta \right|}^2\right)dz=\mathrm{Re}\frac{\beta d^2{H}^{\prime }}{\kappa }{\displaystyle \underset{0}{\overset{1}{\int }}{\Theta }^{*}Wdz=\frac{\beta d^2{H}^{\prime }}{\kappa }\mathrm{Re}{\displaystyle \underset{0}{\overset{1}{\int }}{\Theta }^{*}Wdz.}}}$ (33)

Now

$\begin{array}{l}\mathrm{Re}{\displaystyle \underset{0}{\overset{1}{\int }}{\Theta }^{*}Wdz\le \left|{\displaystyle \underset{0}{\overset{1}{\int }}{\Theta }^{*}Wdz}\right|}\le {\displaystyle \underset{0}{\overset{1}{\int }}\left|{\Theta }^{*}W\right|dz}\le {\displaystyle \underset{0}{\overset{1}{\int }}\left|\Theta \right|\left|W\right|dz}\le \\ \sqrt{{\displaystyle \underset{0}{\overset{1}{\int }}{\left|\Theta \right|}^2}dz}\sqrt{{\displaystyle \underset{0}{\overset{1}{\int }}{\left|W\right|}^{2}dz}}.\end{array}$ (by Schwartz inequality)

Equation (32) and inequality (33) implies that

${\displaystyle \underset{0}{\overset{1}{\int }}\left({\left|D\Theta \right|}^2+a^2{\left|\Theta \right|}^2\right)dz\le \frac{\beta d^2{H}^{\prime }}{\kappa }\sqrt{{\displaystyle \underset{0}{\overset{1}{\int }}{\left|\Theta \right|}^{2}dz}}\sqrt{{\displaystyle \underset{0}{\overset{1}{\int }}{\left|W\right|}^{2}dz}},}$ (34)

which in turn implies that

${\displaystyle \underset{0}{\overset{1}{\int }}{\left|D\Theta \right|}^{2}dz\le \frac{\beta d^2{H}^{\prime }}{\kappa }\sqrt{{\displaystyle \underset{0}{\overset{1}{\int }}{\left|\Theta \right|}^{2}dz}}\sqrt{{\displaystyle \underset{0}{\overset{1}{\int }}{\left|W\right|}^{2}dz}},}$ (35)

hence we derive from inequality (35) using Rayleigh-Ritz inequality

${\displaystyle \underset{0}{\overset{1}{\int }}{\left|D\Theta \right|}^{2}dz\ge {\pi }^2{\displaystyle \underset{0}{\overset{1}{\int }}{\left|\Theta \right|}^{2}dz,}}\left(\text{since}\Theta =0atz=0andz=1\right)$ (36)

$\sqrt{{\displaystyle \underset{0}{\overset{1}{\int }}{\left|\Theta \right|}^{2}dz}}\le \frac{\beta d^2{H}^{\prime }}{{\pi }^2\kappa }\sqrt{{\displaystyle \underset{0}{\overset{1}{\int }}{\left|W\right|}^{2}dz}}.$ (37)

Inequalities (34) and (37) lead to

${\displaystyle \underset{0}{\overset{1}{\int }}\left({\left|D\Theta \right|}^2+a^2{\left|\Theta \right|}^2\right)dz\le {\left(\frac{\beta d^2{H}^{\prime }}{\pi \kappa }\right)}^2{\displaystyle \underset{0}{\overset{1}{\int }}{\left|W\right|}^{2}dz,}}$ (38)

and hence the lemma.

The contents of the above lemma when presented otherwise from the point of view of theoretical hydrodynamics imply that

Lemma: A necessary condition for the validity of the principle of exchange of stabilities in thermal convection configuration of Walters B' viscoelastic fluid in porous medium in the presence of magnetic field and suspended particles is that

${\displaystyle \underset{0}{\overset{1}{\int }}\left({\left|D\Theta \right|}^2+a^2{\left|\Theta \right|}^2\right)dz\le {\left(\frac{\beta d^2{H}^{\prime }}{\pi \kappa }\right)}^2{\displaystyle \underset{0}{\overset{1}{\int }}{\left|W\right|}^{2}dz.}}$ >

We now prove the following theorem:
Theorem: If $\left[\sigma ={\sigma }_r+i{\sigma }_i,W,\Theta ,X\right]$ is a non-trivial solution of the double eigen value problem for ${\sigma }_{r}and{\sigma }_i$ described by the equations (21)-(23) with the boundary conditions (25) for given values of other parameters, then a sufficiency condition for the invalidity of $\sigma =0\left(i.e.{\sigma }_r={\sigma }_i=0\right)$ to be an Eigen value is that $\frac{R{H}^{\prime }{P}_l}{{\pi }^2}<1.$

Proof: Multiplying equation (21) by W*, the complex conjugate of W, integrating over the range of z and using equations (22) and (23) together with the boundary conditions (25), we obtain

$\begin{array}{l}\left[\frac{{\sigma }^{\prime }}{\in }+\frac{1}{P_{\mathcal{l}}}\left(1-F\sigma \right)\right]I_1-\frac{g\alpha \kappa a^2}{\upsilon \beta }\left[\frac{d^2+\upsilon \tau {\sigma }^{*}}{H^{\prime }{d}^2+\upsilon \tau {\sigma }^{*}}\right]\left[I_2+\overline{E+h\in }{p}_1{\sigma }^{*}{I}_3{}^{{}^{}}\right]\\ +\frac{{\mu }_e\eta \in }{4\pi {\rho }_0\upsilon }\left[I_4+p_2{\sigma }^{*}{I}_5{}^{{}^{{}^{}}}\right]=0,\end{array}$ (39)

where

$\begin{array}{l}{I}_1={\displaystyle {\int }_0^1\left({\left|DW\right|}^2+a^2{\left|W\right|}^2\right)dz,I_2=}{\displaystyle {\int }_0^1\left({\left|D\Theta \right|}^2+a^2{\left|\Theta \right|}^2\right)dz,}\\ I_3={\displaystyle {\int }_0^1{\left|\Theta \right|}^{2}dz,I_4=}{\displaystyle {\int }_0^1\left({\left|D^{2}X\right|}^2+2a^2{\left|DX\right|}^2+a^4{\left|X\right|}^2\right)dz,}\\ I_5={\displaystyle {\int }_0^1\left({\left|DX\right|}^2+a^2{\left|X\right|}^2\right)dz,}\end{array}$

and $\sigma *$ is the complex conjugate of σ. The integrals I₁, I₂, …., I₅ are all positive definite.

Putting ${\sigma }_r=0$ and $f=\frac{m{N}_0}{{\rho }_0}$ in equation (39) and separating the real and imaginary parts of the resulting equation, we derive

$\begin{array}{l}\frac{1}{P_l}{I}_1-\frac{g\alpha \kappa a^2}{\nu \beta \left({H^{\prime }}^2{d}^4+{\nu }^2{\tau }^2{\sigma }_i^2\right)}\left[\begin{array}{l}\left(d^2{H}^{\prime }+{\nu }^2{\tau }^2{\sigma }_i^2\right)I_2+\nu \tau {\sigma }_i{d}^2\overline{E+h\in }{p}_1{\sigma }_i{I}_3\\ -\nu \tau {\sigma }_i^2{H}^{\prime }{d}^2\overline{E+h\in }{p}_1{I}_3\end{array}\right]\\ +\frac{{\mu }_e\eta \epsilon }{4\pi {\rho }_0\nu }{I}_4=0\end{array}$ (40)

and

$\begin{array}{l}i{\sigma }_i[\left\{\frac{1}{\in }\left(1+\frac{f}{1+p_1^2{\tau }^2{\sigma }_i^2}\right)-\frac{F}{P_{\mathcal{l}}}\right\}{I}_1+\frac{g\alpha \kappa a^2}{\upsilon \beta \left({H^{\prime }}^2{d}^4+{\upsilon }^2{\tau }^2{\sigma }_i^2\right)}\{d^2\upsilon \tau h{I}_2{}^{{}^{{}^{{}^{}}}}\\ +p_1\overline{E+h\in }{\left(H^{\prime }{d}^4+{\upsilon }^2{\tau }^2{\sigma }_i^2\right)}^{{}^{}}{I}_3\}-\frac{{\mu }_e\eta \in p_2}{4\pi {\rho }_0\upsilon }{I}_5]=0.\end{array}$ (41)

Equations (40) and (41) must be satisfied when ${\sigma }_r=0$ . Further since ${\sigma }_i$ is also zero as a necessary condition of the theorem, equation (41) is identically satisfied while equation (40) reduces to

$\frac{1}{P_l}{I}_1-\frac{g\alpha \kappa a^2}{\nu \beta H^{\prime }{d}^2}{I}_2+\frac{{\mu }_e\epsilon \eta }{4\pi {\rho }_0\nu }{I}_4=0.$ (42)

Now making use of inequality (38) and the inequality

${\displaystyle \underset{0}{\overset{1}{\int }}\left({\left|DW\right|}^2+a^2{\left|W\right|}^2\right)dz\ge a^2{\displaystyle \underset{0}{\overset{1}{\int }}{\left|W\right|}^{2}dz}}$ , (which is always valid),

we derive from the equation (42)

$\begin{array}{l}\left\{\frac{1}{P_l}{I}_1+\frac{g{a}^2\alpha \kappa }{\nu \beta H^{\prime }{d}^2}{I}_2+\frac{{\mu }_e\epsilon \eta }{4\pi {\rho }_0\nu }{I}_4\right\}>\\ \left\{\frac{a^2}{P_l}\left[1-\frac{H^{\prime }{P}_{l}R}{{\pi }^2}\right]{\displaystyle \underset{0}{\overset{1}{\int }}{\left|W\right|}^{2}dz+\frac{{\mu }_e\epsilon \eta }{4\pi {\rho }_0\nu }{I}_4}\right\},\end{array}$ (43)

where $R=\frac{g\alpha \beta d^4}{\nu \kappa }$ is the thermal Rayleigh number.

Now if $\frac{H^{\prime }{P}_{l}R}{{\pi }^2}<1$ , then the right hand side of inequality (43) is a positive definite which in turn implies that the left hand side of the inequality (43) must also be positive definite and therefore (42) cannot be satisfied. Thus a sufficiency condition for the invalidity of zero being an Eigen-value for $\sigma$ is that $\frac{H^{\prime }{P}_{l}R}{{\pi }^2}<1$ .

It is clear from above that when regions outside the fluid are perfectly conducting

$a\left\{{\left({\left|K\right|}^2\right)}_1+{\left({\left|K\right|}^2\right)}_0\right\}=0,$ (44)

and hence the above analysis holds good for this case.

Presented otherwise from the point of view of theoretical hydrodynamics, we have the following theorem:

Theorem: A sufficiency condition for the invalidity of principle of exchange of stabilities in a thermal convection configuration of Walters B' viscoelastic fluid in porous medium in the presence of suspended particles and magnetic field is that the thermal Rayleigh number $R$ , the medium permeability $P_l$ and suspended particles parameter $H^{\prime }$ are restricted by the inequality $\frac{H^{\prime }{P}_{l}R}{{\pi }^2}<1$ ,

or in the context of over stability, we can state the above theorem as:

Theorem: A sufficiency condition for the existence of overstability in a thermal convection configuration of Walters B' viscoelastic fluid in porous medium in the presence of suspended particles is that the thermal Rayleigh number $R$ , medium permeability $P_l$ and suspended particles parameter $H^{\prime }$ are restricted by the inequality $\frac{H^{\prime }{P}_{l}R}{{\pi }^2}<1$ .

Stability of the system and oscillatory modes

Equation (41) yields that ${\sigma }_i=0$ or ${\sigma }_i\ne 0$ , which means that modes may be non-oscillatory or oscillatory. In the absence of magnetic field and viscoelasticity, equation (41) reduces to

$\begin{array}{l}i{\sigma }_i[\left\{\frac{1}{\in }\left(1+\frac{f}{1+p_1^2{\tau }^2{\sigma }_i^2}\right)\right\}{I}_1+\frac{g\alpha \kappa a^2}{\upsilon \beta \left({H^{\prime }}^2{d}^4+{\upsilon }^2{\tau }^2{\sigma }_i^2\right)}\{d^2\upsilon \tau h{I}_2{+}^{{}^{{}^{{}^{}}}}\\ +p_1\overline{E+h\in }{\left(H^{\prime }{d}^4+{\upsilon }^2{\tau }^2{\sigma }_i^2\right)}^{{}^{}}{I}_3\}]=0\end{array}$ (45)

and the quantity inside the brackets is positive definite. Thus ${\sigma }_i=0$ , which means that oscillatory modes are not allowed and the principle of exchange of stabilities is valid. The magnetic field and viscoelasticity introduce oscillatory modes (as ${\sigma }_i$ may not be zero) in the system which was non-existent in their absence.

A layer of Newtonian fluid heated from below, under varying assumptions of hydrodynamics and hydromagnetics, has been studied by Chandrasekhar.¹ With the growing importance of non-Newtonian fluids in chemical engineering, modern technology and industry, the investigations on such fluids are desirable. The Walters B' fluid is one such important non-Newtonian (viscoelastic) fluid. Keeping in mind the importance of non-Newtonian fluids, the present paper considered the effect of suspended particles on the Walters B' viscoelastic fluid heated from below in porous medium in the presence of a uniform horizontal magnetic field.

The main conclusions from the analysis of this paper are as follows:

1. For the case of stationary convection the following observations are made:
1. The viscoelastic parameter F vanishes with σ and Walters B′ viscoelastic fluid behaves like an ordinary Newtonian fluid.
2. The magnetic field is found to postpone the onset of convection whereas the medium permeability and suspended particles hasten the onset of convection.
2. It is also observed from Figures 1-3 that the magnetic field postpones the onset of convection while medium permeability and suspended particles hasten the onset of convection.
3. A necessary condition for the validity of the principle of exchange of stabilities in thermal convection configuration of Walters B' viscoelastic fluid in porous medium in the presence of magnetic field and suspended particles is that

${\displaystyle \underset{0}{\overset{1}{\int }}\left({\left|D\Theta \right|}^2+a^2{\left|\Theta \right|}^2\right)dz\le {\left(\frac{\beta d^2{H}^{\prime }}{\pi \kappa }\right)}^2{\displaystyle \underset{0}{\overset{1}{\int }}{\left|W\right|}^{2}dz.}}$

4. The magnetic field and viscoelasticity introduce oscillatory modes in the system which was non-existent in their absence.
5. A sufficiency condition for the existence of over stability in a thermal convection configuration of Walters B' viscoelastic fluid in porous medium in the presence of suspended particles is that the thermal Rayleigh number R medium permeability $P_l$ and suspended particles parameter $H^{\prime }$ are restricted by the inequality $\frac{H^{\prime }{P}_{l}R}{{\pi }^2}<1$ .

None.

The authors declare that there is no conflicts of interest regarding the publication of this paper.