An analysis of water consumption for all uses in Cuba shows that the volume of water planned for the whole country, agricultural activities consume 50% each year and approximately 40% of this volume been used for irrigation of the rice crop, Dorticos (2012). Surface irrigation systems classified as those with the lowest efficiency in water use, with average values lower than 60%; being the lowest among all the irrigation techniques used in the country. This situation justifies the use of more efficient irrigation techniques, which propitiate the highest crop yields and contribute to mitigate the effects of climate change. In the paper are compared, three variants design of drip irrigation system in citrus crops, for a real case study in the central region of Cuba: Using the procedures followed from the field tests; using tabulated values proposed by other authors; and applying an alternative procedure used in the design practice of these irrigation systems. The results demonstrate the need to carry out field tests as a premise to design drip irrigation systems and as a guarantee of the rational use of water and energy in the face of climate change.

Keywords: localized irrigation, drip emitter, flow, volume, wet bulb

Due to its regular nature, laminar flow is simpler to analyze than turbulent flow. However, most of the problems that arise in the design of pressurized hydraulic networks belong to the domain of the turbulent regime. The identification of one or the other is done through the Reynolds Number (Re). Osborne Reynolds (1842-1867) was born in Belfast, Ireland, and developed experiments that allowed him to present a series of theories that are still valid today.

$\text{R}e\mathrm{<mo>=</mo>}\frac{V\times \varnothing }{\iota }$ (1)

Donde:

V.-Average speed in the pipe $(m/s)$

$\varphi$ -Inside diameter ofthe pipe (m)

U.-Kinematic viscosity $(m^2/s)$

$Re\le 2000$ Laminar flow

$\mathrm{2000<mo><</mo>}Re\mathrm{<mo><</mo>4000}$ Transitional Regime

$Re\ge 4000$ Turbulent flow

$4000\le Re\le \mathrm{10<mo>/</mo><mo\; stretchy="false">(</mo>}\epsilon \mathrm{<mo>/</mo>}\phi \mathrm{<mo\; stretchy="false">)</mo>}$ Smooth Turbulent Flow

$\mathrm{10<mo>/</mo><mo\; stretchy="false">(</mo>}\epsilon \mathrm{<mo>/</mo>}\phi \mathrm{<mo\; stretchy="false">)</mo><mo><</mo>}Re\mathrm{<mo><</mo>500<mo>/</mo><mo\; stretchy="false">(</mo>}\epsilon \mathrm{<mo>/</mo>}\phi \mathrm{<mo\; stretchy="false">)</mo>}$ Transitional Turbulent Flow.

$\epsilon$ : Equivalent absolute roughness of the pipe wall, $\text{m}\mathrm{.}$

$\delta \text{L}$ : Thickness of the boundary layer, $\text{m}\mathrm{.}$

In pressurized irrigation systems the water is distributed by means of generally circular pipes, a full section, it is applied to the crops by means of emission devices that deliver the flow by dissipating the energy. According to Caupers and Junior¹, the formulation of Torricelli offers an accurate approach to estimate the flow rate delivered by an irrigation emitter; it is valid for large tanks with an outlet in the sidewall Figure 1.

Figure 1 Estimate of the Speed in holes.

Applying Bernoulli between A and B and taking as reference Z = 0. Where B is the contracted section and A and B are opento the atmosphere P =patm.

$Z_A+\frac{P_A}{\gamma }+\frac{V_A^2}{2g}=Z_B+\frac{P_B}{\gamma }+\frac{V_B^2}{2g}\mathrm{.}$

Z: position height

$\frac{p}{\gamma }$ :pressure loading

$\frac{v^2}{2g}$ :load at speed

Considering

$\frac{P_A}{\gamma }{\mathrm{<mo>=</mo>0}}_t;\frac{V_A^2}{2g}\mathrm{<mo>=</mo>0<mo>;</mo>}\frac{P_B}{\gamma }\mathrm{<mo>=</mo>0.}$ Thus:

$V_B\mathrm{<mo>=</mo>}\sqrt[2]{2g\times \mathrm{<mo\; stretchy="false">(</mo>}{Z}_A-Z_B\mathrm{<mo\; stretchy="false">)</mo>}}$

$V_B\mathrm{<mo>=</mo>}\sqrt[2]{2gH}$ (2)

The evolution of these emission devices, which take water from pressure pipes has been extremely wide (from localized irrigation emitters that deliver less than 2L/h to spray nozzles that deliver more than 100L/h), hydraulic operation of the same varies from the Laminar regime to the full Turbulence, López Sánchez.² Starting from (2), you can define the flow rate delivered by a spray nozzle by means of:

$Q\mathrm{<mo>=</mo>}Cc\times Cv\times Ao\times \sqrt{2gH}$ (3)

In which, $Cc\times Cv$ is the sprinkler discharge coefficient (Cd) corrected as a function of the coefficient of the jet contraction and the speed coefficient respectively and $Cd\times Ao\times \sqrt{2g}$ is a KD constant for each sprinkler as a function of the geometric characteristics. Admitting that the device works in a Turbulent flow (x = 0.5), equation (2) can be transformed into:

$Q\mathrm{<mo>=</mo>}Kd\times H^X$ (4)

Where (x) is the sprinkler discharge exponent. According to López Sánchez², the value of (x) would be between 0.5 and 1.0, depending on whether the emission device works in Laminar or Turbulent flow. However due to the device that allows a discharge limitation with the increasing pressure (as well as the auto-compensating drip irrigation emitters), the value of (x) can even be less than 0.5. The next Figure 2 shows the flow rate variations of the emitter as a function of the pressure variation for values $0\le x\le 1$ , emitter flow of 4L/h and working pressure $8\le H\le 12$ (mca) Table 1.

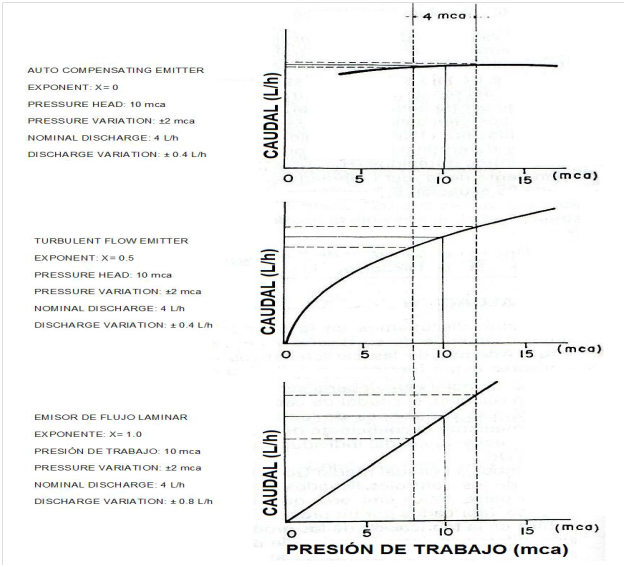
Figure 2 Flow variations of the emitter, Boswell.³

According to Boswell³, the real value of the exponent $\mathrm{<mo\; stretchy="false">(</mo>}x\mathrm{<mo\; stretchy="false">)</mo>}$ for a given emitter can be determined experimentally by working the emitter at two different pressures $\mathrm{<mo\; stretchy="false">(</mo>}{H}_{1}y{H}_2\mathrm{<mo\; stretchy="false">)</mo>}$ . Within the working pressure range of the emitter and carefully measuring the flow rates $\mathrm{<mo\; stretchy="false">(</mo>}{Q}_{1}y{Q}_2\mathrm{<mo\; stretchy="false">)</mo>}$ , then the pairs are drawn on logarithmic paper $\mathrm{<mo\; stretchy="false">(</mo>}{H}_1\mathrm{<mo>;</mo>}{Q}_1\mathrm{<mo\; stretchy="false">)</mo>}\text{y}\mathrm{<mo\; stretchy="false">(</mo>}{H}_2\mathrm{<mo>;</mo>}{Q}_2\mathrm{<mo\; stretchy="false">)</mo>}$ and the slope ofthe line drawn between the two points is measured. It can also be obtained by algebraically deriving equation (4).

$X\mathrm{<mo>=</mo>}\frac{\log \mathrm{<mo\; stretchy="false">(</mo>}\frac{Q_1}{Q_2}\mathrm{<mo\; stretchy="false">)</mo>}}{\log \mathrm{<mo\; stretchy="false">(</mo>}\frac{H_1}{H_2}\mathrm{<mo\; stretchy="false">)</mo>}}$ (5)

The constant $\mathrm{<mo\; stretchy="false">(</mo>}kd\mathrm{<mo\; stretchy="false">)</mo>}$ can also be obtained by clearing (4):

$Kd\mathrm{<mo>=</mo>}\frac{Q}{H^{\chi }}$ (6)

According to López Sánchez² during the hydraulic design of irrigation plots in pressurized systems, in order to ensure adequate emission uniformity, it is important to analyze the dependencies between the relative variations of flow and pressure. In this sense the elementary variation of the flow $\mathrm{<mo\; stretchy="false">(</mo>}dQ\le \mathrm{10<mi>\%</mi><mo\; stretchy="false">)</mo>}$ , corresponding to an elementary variation of the pressure (dH), can also be obtained from (4):

$dQ\mathrm{<mo>=</mo>}Kd\times \chi \times H^{x-1}dH$ (7)

In design practice, it is common to admit a relative variation ofthe flow rate $\mathrm{<mo\; stretchy="false">(</mo>}dQ\le \mathrm{10<mi>\%</mi><mo\; stretchy="false">)</mo>}$ , referred to the nominal or design value ofthe emission devices, thus: $\mathrm{<mo\; stretchy="false">(</mo>}dQ\mathrm{<mo>/</mo>}Q\le \mathrm{0.10<mo\; stretchy="false">)</mo>}$ . So that, as in full turbulence regime $\mathrm{<mo\; stretchy="false">(</mo>}x\mathrm{<mo>=</mo>0.5<mo\; stretchy="false">)</mo>}$ ; the relative pressure variation also referred to the nominal value ofthe emission device is obtained by substituting (6) in (7):

$dQ\mathrm{<mo>=</mo>}\frac{Q}{H^{\chi }}\times x\times H^{x-1}\times dH$

$dH\mathrm{<mo>=</mo>}\frac{dQ}{Q}\times \frac{1}{\chi }\times \frac{H^{\chi }}{H^{x-1}}$

$dH\mathrm{<mo>=</mo>0.2}H$ (8)

If Laminar Flow $\mathrm{<mo\; stretchy="false">(</mo>}x\mathrm{<mo>=</mo>1<mo\; stretchy="false">)</mo>}$ , then:

$dH\mathrm{<mo>=</mo>0.1}H$ (9)

This highlights the influence of the type of emission device and the flow regime on the emission uniformity of the emitters in the irrigation plot. However, the experience in the design has shown that the above is not the only criterion that should be considered when designing an irrigation plot. In the design of drip irrigation systems the criteria are more demanding, for these cases the criterion of uniformity of Kristiansen is not applicable, for them a new coefficient of uniformity (CU) is defined, which can be used for the evaluation of facilities in operation as well as for the design of new facilities. This parameter is a condition that is imposed in the agronomic design and correlates constructive and hydraulic factors, was suggested by (ASAE EP405), cited by Boswell³ and accepted by the US Soil Conservation Service.

$CU\mathrm{<mo>=</mo><mo\; stretchy="false">[</mo><mo\; stretchy="false">(</mo>1}-\frac{1.27\times Cvf}{2_{\sqrt{e}}}\mathrm{<mo\; stretchy="false">)</mo>}\times \mathrm{<mo\; stretchy="false">(</mo>}\frac{Qm{\iota }^{\prime }n}{Qmed}\mathrm{<mo\; stretchy="false">)</mo>}\times \mathrm{100<mo\; stretchy="false">]</mo>}$ (10)

Donde:

$Cvf$ . ‒Fabrication variation coefcient $\mathrm{<mo\; stretchy="false">(</mo>}\text{t}\times \mathrm{1<mo\; stretchy="false">)</mo>}$ .

$e$ . ‒Emitters Number wetting the same plant (u).

$Qmin\mathrm{.}-$ Minimum admissible flow in the irrigation plot $\text{(L}\mathrm{<mo>/</mo>}\text{h)}$ .

Qmed. - Average flow ofthe emitters in the irrigation plot $\mathrm{<mo\; stretchy="false">(</mo>}\text{L}\mathrm{<mo>/</mo>}\text{h}\mathrm{<mo\; stretchy="false">)</mo>}$ .

The term $\mathrm{<mo\; stretchy="false">(</mo>1}-\frac{1.27\times C\nu f}{2_{\sqrt{e}}}\mathrm{<mo\; stretchy="false">)</mo>}$ groups the constructive factors.

The term $\mathrm{<mo\; stretchy="false">(</mo>}\frac{Qmin}{Qmed}\mathrm{<mo\; stretchy="false">)</mo>}$ groups the hydraulic factors.

Three reasons justify the use of this expression (10) instead of the one used in the design of sprinkler irrigation systems (8):

1. The fact that the outlet diameter of the drip emitters is much smaller than the diameter of the sprinkler emitters; generally outlet diameter value oscillates between 0.8 ≤ s ≤ 1.2mm, implies that the risk of obturation is much greater in drip irrigation emitters.
2. Due to the wear occurred by the molds during the manufacturing process, not all drip emitters leave the factory with the same outlet diameter, these affects the uniformity discharge of the emitters in the irrigation plot, then, considering the number of emitters wetting the same plant (e) when estimating (CU); the constructive factor is taken into account with greater rigor in the localized irrigation systems.
3. In drip irrigation systems the incidence of winds in the shape and dimensions of the wet bulbs that are generated is significantly lower than sprinkler irrigation. Considering the hydraulic factor during the design procedure, the relationship between the minimum permissible flow rate in the plot and the nominal flow or design of the emitter have to taking into account, by means of to estimate the losses due to frictions that take place in the network of pipes that make up the irrigation plot, as well as the topographic differences due to the relief; By means of checking that the minimum pressure within the irrigation plot is greater than or equal to a minimum value that is calculated in the pressure tolerance. With the technological advances achieved, the hydraulic component of (CU) has been significantly improved with the auto compensating emitters. However, in spite of the wide range of these that exist in the market, the risk of obturation is still a problem not totally solved and the solutions usually involve expensive filtering systems depending on the quality of the irrigation water.

Pizarro⁴ states; to guarantee a soil moisture content corresponding to the crop water requirements, is important to delimit the value of (e) that guarantees the minimum percentage of wetting (PHum) around the root system; as well as to define the volume delivered by the emitter (Ve) and made available to the plant very close to this area: (90% Prad $\le Pb\le$ 120%Prad). Also refers that the choice $\mathrm{<mo\; stretchy="false">(</mo>}PHum\mathrm{<mo\; stretchy="false">)</mo>}$ is an important issue since at high values, increases the security of the system due to the greater volume of soil moist explored by the roots, facilitating the absorption of water and nutrients; however, high values of $\mathrm{<mo\; stretchy="false">(</mo>}PHum\mathrm{<mo\; stretchy="false">)</mo>}$ also increase the cost of the installation, this aspect being as well as the risk of obturation of the emitters the main drawbacks of this irrigation method. Another important issue is the wetted area by the drip emitter, since the shape and dimensions of the wet bulb generated by these emitters depends on multiple factors, among them the soil texture, the degree of stratification, the irrigation depth, the frequency and timing irrigation and others. For the purposes of design, the estimation of the area wetted by a drip emitter can be done by three procedures: the use of professional software that allows simulating the behavior of the wetting bulb, the use of tables made by other authors and based on the results obtained from field tests. According to Pizarro⁴ the use of modeling software is faced with the mathematical difficulty to integrate the differential equations that are reached after its analysis, as well as to establish its limits of integration and to estimate the hydraulic diffusivity that is the parameter that defines the variation of moisture contents in conditions of non-saturation. Currently there are some of these simulation models, but the difficulty to obtain the data that must be provided to the same together with the acquisition price, makes this not for the moment a viable solution for design purposes. Also refers, that the use of tables will be more inappropriate the more factors are ignored, due to the difficulty of quantifying from the soil properties other important parameters such as the degree of stratification, stoniness and other related to the soil moisture content. Therefore, although very complete tables are available in certain data, their use will suffer from the necessary precision for the design, so they should always be used with great caution. Table 2 that follows shows an example. The use of the results of the field test is currently the most rigorous procedure to design drip irrigation systems. The design is made by trial and error starting from establishing the limits in depth of the wet bulb, foreseeing that the same when at least located very close to the area of dense branching of the roots of the plant. This can be achieved through:

90% Prad $\le p\le$ 120% Prad (11)

Next, the value of (p) between these limits is selected from the results of the field test and the corresponding values of (Ve) and (r) are noted. From (r) the surface moistened by the emitter is calculated by means of:

$Ae\mathrm{<mo>=</mo>}\pi \times r^2$ (12)

Then the minimum number of issuers is determined, which guarantees that the percentage of wetted surface of each plant is higher than a minimum that has been established by several authors:

$e\ge \frac{Amp\times PHmin}{100\times Ae}$ (13)

Keller⁵ recommends the following minimum values of percentage of wet area for the case of trees. Later Torralba^7,8 proposes orientative values of (PHmín) for Cuba conditions Table 3.

The percentages vary from the lower value to the higher when increasing the aridity of the climate and the lightness in texture and stony soil. The frequency of irrigation can be estimated according to the relationship between the volume of water needed by the plant and the volume of water applied by the emitter, which is measured experimentally during the field test and corresponds to the depth and the diameter of the appropriate wet bulb according to the properties of the soil. That is deduced from:

$e\times Ve\mathrm{<mo>=</mo>}l\times Nt$ (14)

The irrigation timing depends on the total water needs and the installed flow per plant this depends on the disposition of emitters that is adopted in relation to the row of plants, the irrigation timing is approximated by excess in fractions of quarter hour to facilitate irrigation scheduling, it can be estimated from:

$Tr\mathrm{<mo>=</mo>}\frac{NT}{e\times Qe}$ (15)

The schedule with interline emitters are not recommended for the case of trees, because it creates a wet strip that is only suitable in dense plantations with not very extensive root systems; it is more justified in the case of irrigation water management in the presence of salts. The dispositions with interline and two lateral emitters per row of plant are not recommended, because it doubles the length of the lateral pipes. The irrigation water depth is calculated based on the number of emitters that moisten the same plant and the volume delivered by each emitter, which have been noted the specifications described above, it is derived from:

$DT\mathrm{<mo>=</mo>}e\times Ve\mathrm{<mo>=</mo>}e\times Qe\times Tr$ (16)

In order to provide a practical approach to the aforementioned, will address the complete design of a rotational unit of localized irrigation, using auto-compensating drippers, to benefit crops of Orange. The design will be carried out by three different procedures but using the same data that define the Water - Soil - Plant - Climate complex for the three variants; so that conclusions can be established to demonstrate the validity of the investigation.

The study case covers a gross area of 1.20 ha, consists of four rectangular irrigation plots of (80m × 200m), located in pairs around the control station. In it, the pumping installation will be concentrated together with the filtering system in order to facilitate irrigation automation. The irrigation plots will be separated at 10m to facilitate the work of harvesting, repair and maintenance of the irrigation system. A perimeter path of 5m is foreseen to facilitate communication with other areas with irrigation perspectives. An underground source of water supply will be assumed, with an authorized flow to extract enough for the irrigation of the proposed crops. Likewise, a coefficient of uniformity CU = 90% will be assumed for the design and the plots will be 200m long. The relief is quite flat, so the pipe network slopes will not be taken into account in the design to facilitate calculations. The design procedure of the first and second variants is conceived based on the procedure proposed by Keller & Rodrigo⁵ the calculation will be made from the data of the field test referred in the Table 4 & 5. For the third variant, an alternative procedure will be used, which is currently used due to the impossibility of performing the field tests.

Table 6 below shows the results of the agronomic design using three different procedures. The data of the field test correspond to those of a medium texture soil and an emitter flow=4L/h. The results of the hydraulic design are shown in Table 7. The net water requirements for drip irrigation were estimated using the procedure proposed by the FAO Committee of Consultants (FAO Penman - Monteith equation), considering the most critical daily evaporation at 10% probability of occurrence to take into account climatic variability (Ev10% P), the crop coefficient (Kc) and the correction coefficient due to the location of the water depth (KL). The total needs were obtained considering an application efficiency = 90% and the salinity risks. As the data for the calculation of the three variants are the same, the results are necessarily the same. Therefore the irrigation water depth should be the same as well.

One is the fact that by means of the field test it is possible to take into account the depth at which the wetting bulb develops. This is an important issue since it foresees the risk of dampening inappropriate depths that lead to increased losses due to deep percolation or to dislodging the wet bulb in relation to the dense root depth area of the plant and worse, can cause important effects for the plants during fertirrigation. It also influences the proper rooting of the plants, which favors the absorption of water and nutrients as well as an anchorage capable of resisting stronger winds.

The actual diameter reached by the wetting bulb at the design depth is obtained based on the results of the field test. This allows us to estimate with considerable precision the surface moistened by the emitter, which is a parameter that allows specify the number of drippers that moisten the same plant and that apply a volume that guarantees the minimum percentage of wetting in each plant. This situation is foreseen in the second variant but from tabulated values, proposed by other authors for specific conditions, which do not necessarily coincide with those of the scenarios of the projects that are carried out Table 2. The value of the bulb diameter was obtained by interpolation in this variant, for root depths and similar physical properties, for instance the surface wetted by emitter was much lower than the first variant, and therefore the number of emitters needed to meet the total water needs of the plant is greater, with a significant impact on the hydraulic design. This reasoning is confirmed due to a daily irrigation frequency is assumed and therefore the irrigation timing is less than in the first variant, so is possible to guarantee the necessary water depth with lower irrigation timing, but on account of using larger diameter of laterals (32 × 27.8), which can increase the initial cost of the installation significantly. When analyzing the deliver volume of water by emitter, according to the soil response determined in the field test, we note that in the second variant each emitter delivers a volume $\approx$ 50% lower than the soil assimilates in favor of the plants; besides, justifying the fact that 14 drippers must be placed instead of 6 that are needed in the first variant, also increasing the initial cost of the investment. Bearing in mind that what is interesting from the agronomic point of view of irrigation is the moisture content very close to the plant and the tensions that this generates in the soil, are a fact the inconveniences that can happen when the design is not carried out from the results of the field test. The mentioned risk becomes more evident with the third variant, since the design does not take into account the analysis of these parameters, and the number of necessary drippers to meet the total water needs of the plant is directly deduced of the water needs along the row of plants, or assumes from the nominal flow and the number of plants in the row. In this variant, the duration and frequency of irrigation are assumed at the convenience of the irrigation operation, foreseeing to deliver the necessary dose in each side of irrigation, as well as the volume of water needed for each plant depending on assuming the duration of irrigation convenient for this purpose; Contrary to what has been established in the practice of design, in which the duration of irrigation is obtained based on the total water needs, the properties of the soil and consequently the installed flow per plant. According to the results for each of the variants Table 5, no significant differences are recognized in the hydraulic design of the installation between the variants developed from the results of the field test and the alternative variant. The rigor of the procedure for the design of the facilities is in function of the appropriate communication between the designer and the investor of the work. The biggest differences are seen in the variant that uses the tabulated values proposed by other authors, this shows the need to perform a very careful analysis when assuming each design parameter.

1. The diameter moistened by the emitter at the dense ruth depth of the crop is a design parameter that allows ensuring a better distribution of water and nutrients for the plants in the drip irrigation systems and must be obtained from the Field tests.
2. The volume to be wetted by the emitter is a parameter that can increase the frequency ant timing irrigation, therefore it must be obtained experimentally or using modeling software calibrated for the project conditions.
3. Failure to consider the results of field tests can lead to over sizing irrigation systems as well as affecting crop yields and decreasing water productivity in drip irrigation systems.

None.

The author declares that there is no conflict of interest.

1. Amir I. Sprinkle and Trickle Irrigation. International Institute for Infrastructural, Hydraulic and Environmental Engineering. The Netherlands: IHE Delft; 1998.
2. Boswel MJ. Micro Irrigation Design Manual. España Sevilla; 1990.
3. Caupers C Junior E. Hidráulica 1. Apuntamentos das aulas teóricas. Universidad Eduardo Mondlane. Maputo Mozambique; 2007.
4. Keller JB. Sprinkler and Trickle irrigation. New York: EEUU; 1990.
5. Keller J, Rodrigo J. Trickle irrigation lateral design. ASAE Technical Paper. USA; 1976;(26):79.
6. López Sánchez, JL. Fundamentals of hydraulic calculation in irrigation and drainage systems. España: Mundi editions Press; 2003.
7. Pizarro CF.“High Frequency Localized Irrigation: Drip, Microaspersion and Exudation”. Madrid, España: Mundi editions Press; 1996.
8. Torralba V. Localized irrigation, concepts, agronomic peculiarities and basic data. Agronomic and hydraulic design. Cuba:Ciudad Habana; 1990.