eISSN: 2577-8242


An experimental study of Newtonian and non-Newtonian droplets rising in Newtonian and non-Newtonian fluids is presented when the droplets are subjected to external ultrasonic waves. Our results show that significant changes in the drop drag coefficient are observed when the external fluid is non-Newtonian. When the external fluid is Newtonian, for both Newtonian and non Newtonian droplets the changes in terminal speed and drag coefficient are small. Our results indicate that the ultrasound has a significant effect on the properties of non Newtonian media, probably inducing changes in the effective viscosity and in the entanglement of the suspended polymer molecules.
Keywords: viscoelastic drop, ultrasound, shear-thinning fluid, terminal velocity
Processes such as coating, painting, blending of molten polymers, food processing and fabrication of immiscible liquid-liquid suspensions are examples in which the dynamics of droplet motion is of paramount importance in order to obtain an optimum design.1−3 Previous studies show that the dynamics of non-buoyant Newtonian drops in Newtonian fluids moving under creeping flow conditions is determined by three dimensionless parameters: the capillary number, the viscosity ratio and the density ratio. Drop deformation increases with increasing capillary number until the drop breaks up at a certain critical capillary number. This break-up occurs in the flow direction as the volume of the drop increases and the free surface of the drop deforms from a spherical shape to elongated slender forms.4−5
However, for systems involving viscoelastic components, the study of drop dynamics is not quite simple. It has been shown that in simple shear flow, viscoelastic properties of the droplet tend to reduce deformation, while in the continuous phase the deformation is reduced or increased depending on whether the Deborah number is low or high.6−9 In extensional flow, viscoelasticity of the droplet reduces deformation while its presence in the continuous surrounding phase enhances it.10−12 More recently, Zhou et al.,13 and Yue et al.,14 showed using finite element methods that the scheme mentioned above applies only when both capillary and viscosity ratio numbers are small; if they are large, however, the opposite effect is produced. Moreover, Sibillo et al.,15 reported that the onset of drop deformation has a time dependent rheology. Finally, the critical capillary number for non-Newtonian droplet break-up increases with drop viscoelasticity and decreases with matrix viscoelasticity; the latter enhances droplet orientation and break up in the flow direction, whilst break up along the vorticity direction can be achieved at high shear rates.16,17 In addition, the droplet undergoes several cycles of oscillations before breaking up in the vorticity direction.18,19
All experimental studies mentioned above have also been predicted theoretically by different authors.20−25
However; in order to enhance mechanical properties in polymer blending, plastic recycling, and food processing, acoustic energy is used in the form of piezoelectric ultrasound in single screw and twin-screw extrusion26,27 and also for its potential use as a preservation tool in food industry.28 The propagation of small amplitude acoustic waves in fluids that contain particles is an old and much studied subject, both from the fundamental and applied points of view. Further, in some instances, theoretical formulations exist that have not received experimental corroboration. Such is the case of models where attenuation can be well predicted but fails to describe dispersion.29 In other cases, substantial differences has been observed between attenuation coefficients from those obtained experimentally. To a complete revision of literature about different aspects of theoretical model predictions see reference.30 That´s why, the present study represents a good challenge to predict attenuation coefficients in these systems.
Moreover the correct prediction of attenuation and dispersion of waves can help well-established methods for detection of corrosion defects in pipelines31 and curved pipes.32,33 Additionally, compression waves can also propagate in solids. However, in solids unlike in fluids, a shearing strain produced at some point can be transmitted to adjacent layers by the strong binding between particles. This mechanism generates transverse waves also called bulk shear waves. Such is the case of drilling fluids. Very recently Ambar Veg et al.,34,35 have shown nanofluids can resolve a number of issues including borehole instability and lost circulation in drilling wells. Knowing the process of attenuation and dispersion of ultrasound waves can help to obtain a better dispersion of nano-particles in the WBM.
In what follows, the dynamics of Newtonian and non-Newtonian drops rising in Glycerol (Newtonian) and Polyethylene oxide (Non-Newtonian) under the influence of an energy acoustic field is investigated. Physical mechanisms involved in the rising velocity of droplets are examined using rheological measurements together with simultaneous application of ultrasonic pulses.
To our knowledge, there is no previous study involving the use of ultrasonic field in droplets rising in different fluids.
The experimental arrangement is shown schematically in Figure 1. The device consists of a cylindrical container of 60cm in length and 5cm in diameter which has a test section where the drops are injected. The container has a valve at the bottom connected to a syringe which releases the droplets into the solution at the center of the container to reduce wall effects. The cylindrical container is located inside a rectangular tank made of glass, with 150cm height and 20.5cm width filled with water. The similarity of the refraction indices of glass and water reduces refraction effects of the curved cylinder-water interface. A piezoelectric transducer (40Hz and 50Watts) is located at the top of the internal cylinder and its surface is in contact with that of the fluid. Measurements of rising drop velocity and shape aspect ratio were obtained using a Canon camera EOS 60D with a macro lens of 100mm size. Photographs of the drops were taken during their passage through the column. The camera was mounted on one side of the viewing section and was focused on a standard glass sphere held at the center of the column. Two electric lamps (200W) were placed 30cm from the backside of the column to illuminate the drop from the side. After taking photographs an image processing analysis was carried out using the image processing tools of Matlab.36−39 Shape of the drops was represented in terms of eccentricity (E) of the drop defined as the ratio of its largest horizontal dimension to the larger vertical dimension.
Newtonian liquids: Glycerol, Glycerol-water, were used as Newtonian external fluid whilst Roshframs motor oil was used as a Newtonian droplet.
Non-Newtonian liquids: Aqueous solutions of Polyethylene oxide in distilled water were used as the external fluid and a well known and widely used solution of Polyisobutelene, in Decalin and Polybutene oil was used as the viscoelastic droplet.
Solutions of Glycerol in water at 85%, Polyethylene oxide in water at 0.5% per weight, Polyisobutylene (PIB) at 2.5% in 47.5% Decalin and 50% Polybutene oil were used. The Polyisobutylene solution also known as S1 fluid was prepared following the methodology reported elsewhere in40 and is not described here. A TA Instruments G2 stress-controlled rheometer was used to measure the viscosity and first normal stress difference flow curves, in the shear rate range of 0.01–100 s−1. Small amplitude oscillatory shear flow was used to obtain the variation of the loss G’ and storage G’’ modulus with frequency at 22°C. Tests were performed with the cone and plate fixture, with 4 cm diameter and 1.59.14° cone angle. A controlled strain rheometer (AR-1000 TA Instruments) was modified with a 40mm lower plate transducer (40Hz and 75W). Measurements of viscosity were performed with a simultaneous application of ultrasonic pulses. The rheological behavior was determined at a constant shear rate (3s-1) for a period of thirty minutes. For the first 5 minutes the fluid was allowed to reach a constant viscosity; an ultrasonic pulse was applied for a further 5 minutes, to finally stop the pulse in order to analyze its effect on the structure of the fluid. For the Newtonian fluids, the viscosities, both glycerol and motor oil showed a constant value of 0.109 and 0.479 Pa*s respectively.
In Figures 2, the shear viscosity and first normal stress difference under simple shear are plotted vs. shear rate for polyethylene oxide (POE) and S1 fluid. At low shear rates the first Newtonian region, where the viscosity is constant, spans over one decade for POE fluid and for two decades of shear rates for S1 fluid. For moderate shear rates to high shear rates, 1 to 100s−1, shear thinning is apparent in the POE fluid; however, shear-thinning for S1 fluid appears at high shear rates, from 10 to 100s−1. First normal stress difference appears at shear rates greater than ten for S1 fluid. Polyethylene oxide does not show normal stress difference for the concentration used.
Figure 3 shows the linear viscoelastic data in the frequency range from 0.1 to 100rad/s for the non-Newtonian fluids. For both fluids, the magnitude of loss modulus is larger than the storage modulus, implying that both fluids exhibit viscous behavior for all frequency intervals. The cross-over frequency, not seen in experimental results, implies a small value of relaxation time with concentration.
Drop velocity as a function of time
Experiments were performed releasing drops of a single size of glycerol and motor oil in a Newtonian fluid and in a non-Newtonian fluid. This was repeated four to six times and then the average value was used for further calculations. The characteristic velocity profile with and without the influence of power ultrasound is depicted in Figures 5 to 8 for the four systems explored.
Newtonian droplet in a Newtonian external fluid
In the case of a motor oil drop rising in glycerol (Figure 4), the velocity increases when the ultrasound field is applied. As time progresses, a slight increase in velocity may be observed; due to the approach of the droplet to the top of the container where the ultrasound field is applied and possible acoustic “cavitation” may be present. In the absence of ultrasound, the velocity is nearly constant.
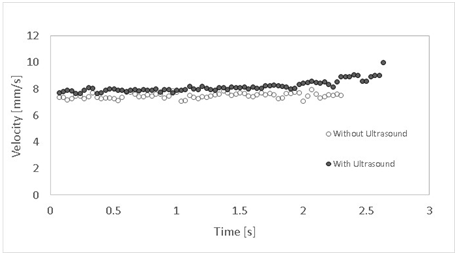
Figure 4 Drop velocity as a function of time for a motor oil drop rising in glycerol with and without the influence of an external ultrasound field.
Newtonian droplet in a non-Newtonian external fluid
In Figure 5, the velocity profile of the Newtonian oil drop moving along the tube shows an increment of velocity of nearly twice the original velocity when the ultrasound is applied. This increase in velocity is probably caused by displacement of physical entanglements of polyethylene oxide molecules. This causes the drop to move across a solvent which now has a lower viscosity. As the drop moves along the container we observe a decrease in velocity in the region of increasing acoustic wave presence. Again, as the drop approaches the final stage, there are less polyethylene oxide molecules due to the proximity of the piezoelectric ultrasound source. This causes the droplet to be exposed basically to the viscosity of the solvent (water), resulting in a substantial increase in its velocity. As a comparison, the velocity without the ultrasound is practically constant throughout the entire path of the droplet.

Figure 5 Drop velocity as a function of time for a motor oil drop rising in Polyethylene oxide solution with and without the influence of an external ultrasound field.
Non-Newtonian droplet in a Newtonian external fluid
In Figure 6, the velocity profile of an S1 droplet rising in glycerol is shown. In this case the droplet velocity is not significantly affected by the presence of the ultrasound field. In this case, only a small volume of non Newtonian fluid is present. Hence, the effect of ultrasound, which allegedly affects only the non Newtonian media more significantly, is minor.
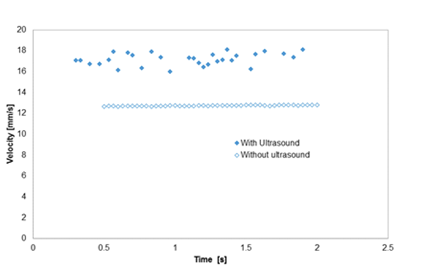
Figure 6 Drop velocity as a function of time for a S1 drop rising in glycerol solution with and without the influence of an external ultrasound field.
Non-Newtonian droplet moving in a non-Newtonian external fluid
The last system shows an S1 droplet rising in a non-Newtonian POE fluid (Figure 7). In this case we observe a monotonic increase in droplet velocity when compared to the case where no power ultrasound is present. In this instance no reduction of drop velocity is observed, which means that all energy coming from the ultrasound waves is being used to break up physical entanglements of the POE solution.
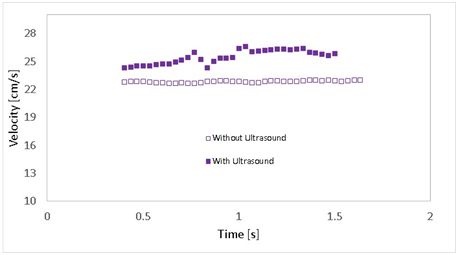
Figure 7 Drop velocity as a function of time for a polyethylene drop (S1 fluid) rising in polyethylene oxide solution with and without the influence of an external ultrasound field.
It is important to note that for all cases, the droplets were not significantly deformed under the action of the ultrasound field. We measured a maximum change of 5% of the drop aspect ratio for all cases. Therefore, changes in the terminal velocity cannot be attributed to changes in shape.
Dimensionless numbers
Using the observed terminal velocity, rheological parameters, interfacial tension and physical properties of the dispersed and continuous phase three dimensionless groups, Re, Ca and Eö were calculated. The physical properties of the droplets and the range of the experimental parameters attained for each system are shown in Table 1.
Drop-Fluid (disperse-continuous) |
Viscosity ratio |
Density ratio |
Ca |
Re |
Eö |
|||
WU |
U |
WU |
U |
WU |
U |
|||
Oil-Glycerol |
4.39 |
0.73 |
2.4X10-5 |
2.8X10-5 |
1.4X10-1 |
2.0X10-1 |
4.5X10-4 |
4.9x10-4 |
Oil-POE |
2.95 |
0.89 |
7.6X10-5 |
7.6X10-5 |
8.5x10-1 |
1.01 |
5.8X10-4 |
5.8X10-4 |
S1-Glycerol |
Shown in Figure 6 |
0.72 |
2.9X10-5 |
2.8x10-5 |
2.1X10-1 |
0.197 |
5.6X10-4 |
4.9X10-4 |
S1-POE |
Shown in Figure 6 |
0.88 |
4.4X10-5 |
5.9X10-5 |
5.1X10-1 |
0.602 |
1.4x10-3 |
1.2X10-3 |
Table 1 Physical parameters and values of dimensionless numbers for the four systems used. The dimensionless groups are calculated with the effect of ultrasound (U) and without it (WU)
For this problem, the relevant dimensionless numbers are defined as: Reynolds number Re, Capillary number Ca, Eötvos number Eo, Viscosity ratio and Density ratio δ defined as: , where is the drop density, is the fluid density, a is the sphere radius, U is the terminal velocity, is the shear viscosity, is the interfacial tension, drop viscosity, fluid viscosity.
The characteristic shear rate of the flow is: . The interfacial tension was obtained measuring the surface tension of all fluids and then applying Antonoff’s rule.
It should be noted that for all systems employed, interfacial forces prevail over viscous forces. This, in addition to a small value of the Eötvos number, may explain why there is no change in droplet shape during the ascent inside the different fluids considered, as predicted by Clift et al.41 Additionally, the influence of inertial forces is not significant since the Reynolds number is less than one.
The experimental results described here show that there is an increase in the velocity magnitude of droplets rising in both Newtonian and non-Newtonian fluids when they are under the influence of an ultrasonic field. The velocity of the droplet varies according to the rheological nature of the fluids involved. Newtonian droplets show a virtually stationary velocity profile under ultrasound influence. Non-Newtonian droplets are more susceptible to absorb ultrasound waves causing substantial changes in velocity. In the case of polyethylene oxide as an external fluid, the ultrasound waves appear to modify the internal structure, changing the rheological properties of the media. Additional physical mechanisms that might be responsible for these variations in velocity profiles were dismissed due to the low values of Reynolds, Eötvös and Capillary numbers obtained.
R. Cedeño-Madera, acknowledges CONACYT for support during her graduate studies.
Author declares there is no conflict of interest in publishing the article.

© . This is an open access article distributed under the terms of the, which permits unrestricted use, distribution, and build upon your work non-commercially.