In this study, we consider the development of a Mars airplane with a fixed wing, which is predicted to be a new Mars observation platform that will enable wide-range observation for Martian exploration. To validate our aerodynamic-design approach using wind tunnels and CFD analyses, we conduct a high-altitude flight test, termed Mars Airplane Balloon Experiment-1 (MABE-1), using Japan Aerospace Exploration Agency (JAXA)’s scientific ballooning (DAIKIKYU) and successfully obtain aerodynamic data for the airplane. This paper describes the results of aerodynamic characteristics from MABE-1 and provides a comparison with the wind tunnel test data.

Keywords: Mars Airplane; Mars Airplane Balloon Experiment (MABE-1); Aerodynamic Characteristics; Wind Tunnel Test

CD: drag coefficient; CL: lift coefficient; D: drag (N); L: lift (N); M: Mach number; Re: Reynolds number; X: Start time of flight test (s); $\alpha$ : Angle of attack (degree); ${\delta }_a$ : Aileron (degree); ${\delta }_e$ : Elevator (degree); ${\delta }_r$ : Rudder angle (degree); NASA: National Aeronautics and Space Administration; ESA: European Space Agency; MELOS: Mars Exploration with Lander-Orbiter Synergy; JAXA: Japan Aerospace Exploration Agency; ARES: Aerial Regional-scale Environmental Survey; L/D: Lift-to-Drag Ratio; LES: Large-Eddy Simulations; DNS: Direct Numerical Simulation; MABE: Mars Airplane Balloon Experiment; RANS: Reynolds Averaged Navier-Stokes; CFRP: Carbon Fiber-Reinforced Plastic; GPS: Global Positioning System

Currently, the National Aeronautics and Space Administration (NASA) and European Space Agency (ESA) have taken lead in Martian exploration using landers and orbiting satellites, and have reported various scientific efforts. In Japan, the next Mars exploration mission, called Mars Exploration with Lander-Orbiter Synergy (MELOS), has been suggested by a Japanese research group that is sponsored by the Japan Aerospace Exploration Agency (JAXA), which marks the initiation of Japanese Martian exploratory research efforts. One option in the Japanese Mars exploration effort is a fixed, main-wing Mars airplane that has been contemplated and studied [1,2].

A Mars airplane would fly and explore the low-density Martian atmosphere at several kilometers altitude with a few hundred kilometers of cruising range and would constitute a new observation platform for future Mars exploration. NASA also studied a Mars airplane, called Aerial Regional-scale Environmental Survey [3] (ARES), in the early 2000s. However, Martian atmospheric flight has several complex technical features that need to be considered in the aerodynamic design of the Mars airplane. For instance, the aircraft will need sufficient lift to sustain its total weight, together with that of attendant scientific equipment, and will require a high lift-to-drag performance for wide-range observation. These demands will be placed on the perspective aircraft despite the restrictions of a low-density Martian atmosphere, which is only 1% of the density of the Earth’s atmosphere. Also, sufficient control surface effectiveness even on Martian atmospheric flight, where the flow easily separates from a wing surface, since we consider acquisition of image data in various places on the Martian surface as one of the objectives. The flight speed cannot be raised excessively in order to acquire image data. Furthermore, we consider that it will be possible to position as a piggyback mission by folding and stored the aircraft in a cylindrical capsule with a dimeter of 1 m. This means that the main wing area is also restricted.

In contrast to commercial earth airplanes, the low-density atmospheric condition and constraints on the flight speed and the main wing area produce a low-Reynolds-number flight $\left(Re=\vartheta ({10}^4)\right)$ . For Reynolds numbers within the range of 104-105, a non-linear lift curve occurs and is associated with the formation or burst of a separation bubble on the wing, so the maximum lift-to-drag ratio (L/D) of smooth airfoils significantly deteriorates due to this early flow separation [4]. In this low-Reynolds-number region, the Ishii airfoil has a comparatively high lift-to-drag performance, and hence, has been considered as the main wing airfoil for the Mars airplane, as designed by JAXA. Both experimental and numerical studies of aerodynamic performance and fluid mechanics of the Ishii airfoil have been conducted in detail [5]. Our research group has performed large-eddy simulations (LES) for investigating the airfoil performance at such Reynolds numbers [6] and confirmed the validity of the LES by comparison with wind tunnel test results. Also, Hosseini et al. [7] reported results of a three-dimensional direct numerical simulation (DNS) of the flow around a wing section at moderate Reynolds numbers. These simulation results show the effectiveness of high-fidelity simulations such as LES and DNS for aerodynamic evaluations of airfoils at low Reynolds numbers. Oyama et al. [1] also designed a Mars airplane with an Ishii airfoil main wing using multi-objective design exploration. Furthermore, the aerodynamic performance and effectiveness of each control surface of the designed Mars airplane have been investigated using a 1/5 scale aircraft model [8,9] and created the aerodynamic model for the avionics design.

The Japanese Mars airplane working group established in 2010 has prepared a high-altitude flight test using a full-scale Mars airplane. This experiment was called Mars Airplane Balloon Experiment-1 (MABE-1) and will be performed at about 36 km altitude, where the flight test environment is equivalent to the Martian atmospheric flight conditions, because of the low gas density and low-temperature conditions. One of the main objectives of MABE-1 was a flight demonstration at such low Re numbers and in low-density atmosphere. In addition, we tried to obtain the basic aerodynamic data (lift and drag coefficients and lift-to-drag ratio) for evaluation of the aerodynamic design based on wind-tunnel tests and CFDs [10]. The aerodynamic performance of the Mars airplane with a complete aircraft configuration was analyzed by Reynolds Averaged Navier-Stokes (RANS) simulation [11]. The simulation results were well validated for the experimental data on aerodynamic coefficients. The flight experiment was conducted on June 12, 2016, at Taiki Aerospace Research Field. Although the aerodynamic data in the glide phase were not obtained, which had been initially intended for measurement, we succeeded in obtaining data for 30 s in the roll-control and pull-up phases. This paper reports the results of the aerodynamic measurement in MABE-1.

Configuration

Three views with external dimensions and an overall picture of the Mars airplane for MABE-1 are shown in Figure 1(a) & 1(b), respectively. The span length, body length, and height are about 2.4, 2.0, and 0.43 m, respectively. A five-hole probe with 0.25m length is mounted on the aircraft nose. This aircraft was designed under constraints that the main wing and the fuselage are folded so that the unit can be housed in a 1-m-diameter-entry capsule. The main wing is separated into inner and outer wings and has a $5°$ dihedral. The Ishii airfoil with high aerodynamic performance at around 23,000 was selected as the main wing airfoil. The results of our wind tunnel tests [9] for investigation of the control surface effectiveness shows that the maneuverability of relatively thin airfoils can improve at such low Reynolds numbers. Thus, the NACA0009 airfoil was used for the vertical and horizontal tail stabilizers. The airplane has two vertical stabilizers, and the planform of the horizontal stabilizer is triangular so that maximum area can be ensured when the fuselage is folded to be housed within the small-entry capsule.

Figure 1: Mars Airplane for MABE-1.

The fuselage and tail wing are composed of carbon fiber-reinforced plastic (CFRP) and balsa wood, respectively. A film was placed on the main wing, which contained a rib structure composed of CFRP. We assumed that the Mars airplane would employ a propeller for propulsion in a future Martian atmospheric flight. However, MABE-1 was conducted as a glider flight test so that the airplane did not employ propeller propulsion, because one of the main objectives of MABE-1 was to obtain basic aerodynamic data. Although the airplane was designed as a folded vehicle housed within a small-entry capsule, as described above, MABE-1 was performed in the unfolded state.

Flight test sensors and devices

Various sensors and devices necessary for the flight test, including avionics units, air data sensors, a DC-DC converter, a battery, a transmitter, a global positioning system (GPS), a parachute, and a rope cutter, were mounted inside the airplane’s fuselage.

The GPS [GARMIN, GPS 15xW] was used for identification of the airplane during the flight. A three-axis angular rate sensor [ANALOGDEVICES, ADXRS300], a three-axis acceleration sensor [ANALOGDEVICES, ADXL210AE], a two-axis geomagnetic azimuth sensor [Dentsukikou, AM-45P], and a dynamic pressure sensor [ALL Sensors Corporation, 0.5 INCH-G-4V] were employed for the flight control.

The five-hole probe was equipped with differential pressure sensors to measure the dynamic pressure, the angle of attack, and the angle of sideslip. These differential sensors were preliminary calibrated by wind-tunnel tests, and the operational tests were conducted under low-pressure and low-temperature conditions using a constant-temperature air reservoir. The sampling rate was 5 Hz. The outputs from each sensor during the flight test are transmitted to a ground station. The details of the method for calculating the aerodynamic coefficients based on the aerodynamic data obtained by these sensors will be described later.

Flight sequence

The flight test sequence of MABA-1 is illustrated in Figure 2. As shown, a gondola (height: 2.5 m, width: 2.9 m, total weight: 220 kg) is covered with foamed materials to protect the Mars airplane from direct sunlight present at high altitude in the Martian atmosphere. The nose of the airplane faces the ground. The gondola was carried up to the target altitude of 36 km by a scientific balloon. After achieving the target altitude, the airplane was separated from the gondola and attitude control was operated in three phases: roll-control phase, pull-up phase, and glide phase. In this flight test, the elevator angle was fixed in each phase to simplify the attitude of the control system and the airplane flew near the trim angle of attack. The ailerons worked in opposition by a differential control, and rudders were deflected to the same direction with the same deflection angle. In addition, a lateral stability control was operated using the dynamic pressure, geomagnetic azimuth, and yaw and roll rates. Yaw or stability control was executed by deflecting ailerons and rudders in each control phase.

Figure 2: Flight test sequence of MABE-1. After the release of the airplane at 36 km altitude, an attitude control was operated in three phases: roll-control phase, pull-up phase, and glide phase.

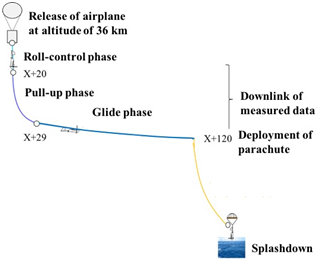
In the roll-control phase, a roll maneuver was performed using ailerons and the yaw control was conducted so that the airplane turned to the direction away from the ground after the pull-up. In the pull-up phase (X+20 s), yaw and roll dampers were engaged. The pull-up was performed at a fixed elevator angle. After the pull-up, the glide phase began (X+29 s). In this phase, the aerodynamic data were obtained at each trim angle of attack $(\alpha =2,4,6°)$ . The parachute was deployed after the acquisition of the aerodynamic data (X+120 s), and the deployed parachute slowly dropped the airplane into the sea. The total flight time was approximately 2 min, with a cruising distance of approximately 13 km.

Acquisition of aerodynamic data

Figure 3 shows a body axis coordinate system (right-handed coordinate system) for the aircraft, and the positive and negative directions of forces and moments acting on the body are defined as shown in Figure 3. In this flight test, lift (L), drag (D), lift coefficient (CL), and drag coefficient (CD) are defined by the following equations:

$L=m\left(-A_{z}cos\alpha +A_{x}sin\alpha \right),$ (1)
$D=-m\left(A_{z}sin\alpha +A_{x}cos\alpha \right),$ (2)
$C_L=L/\left(P_{D}S\right),$ (3)
$C_D=D/\left(P_{D}S\right),$ (4)

Where m is the total weight of the airplane, S is the area of the main wing, and Ax and Az are accelerations along the X and Z axes, respectively. For Ax, Az, PD, and $\alpha$ , values transmitted from each sensor during the flight were used. The angle of attack and dynamic pressure measured by the five-hole probe equipped with the differential pressures are expressed by $\alpha$ and PD, respectively. Each acceleration was obtained from the readout of the acceleration sensors.

Figure 3: Body axis coordinate system (right-handed coordinate system) defining positive and negative directions for forces and moments acting on the aircraft body [8].

Flight history

The flight histories of the altitude and static pressure for 30 s of the flight prior to the glide phase are shown in Figure 4. As shown, the airplane experienced the roll-control and pull-up phases after being released from the gondola at 36 km altitude. The altitude of the aircraft continued to decrease to 33.5 km after 30 s. In association with this decrease in altitude, the static pressure gradually increased from about 800 to 1000 Pa. Figure 5 shows the flight history of the dynamic pressure. The airplane gently accelerated with a decrease in altitude and the dynamic pressure reached approximately 275 Pa after 30 s. This acceleration was greater than our initial assumptions and the recorded dynamic pressure exceeded the maximum measurement range of the differential pressure sensor, 250 Pa. Thus, the dynamic pressure continued to level off during the glide phase. This is the reason why no aerodynamic data were obtained in the initially planned glide phase. We deduced that the generated lift was less than that predicted by the aerodynamic model based on the wind tunnel tests. The details for this conclusion will be described in the next subsection. Therefore, the aerodynamic data obtained for 30 s in the roll-control and pull-up phases will be further discussed in this paper.

Figure 4: Time history of altitude and static pressure.

Figure 5: Flight history of dynamic pressure.

As shown in Figure 6, both the Reynolds number and Mach number monotonically increased for 30 s after the airplane began its flight. Note that the order of the Reynolds number reached 104 and the Mach number reached around 0.65. These specific flow conditions of the low-Reynolds numbers and high-subsonic regime cannot be achieved by the existing wind tunnels. One of the major achievements of MABE-1 is that we succeeded in acquiring aerodynamic data for a full-scale Mars airplane in this flow regime. The Mach number increased almost linearly as the flight proceeded, but the Reynolds number increased only moderately due to the effect of density change associated with the increased static pressure. Wind-tunnel tests of the aerodynamic model were preliminary conducted at Re = 33,000 and 70,000, corresponding to the Reynolds number in the actual flight test at around 11 and 21 s, respectively. However, these two Reynolds numbers were instantaneously exceeded and we obtained only one data plot at each Reynolds number. Thus, we evaluated the aerodynamic data in each Reynolds number range of $\pm 10,000$ . Note that the Ishii airfoil, which is the main wing airfoil of this airplane, has a low Reynolds number dependency on its lift curves at Re greater than 33,000 and at angles of attack that were below the stall angle (about 9°) [12]. Therefore, we concluded that these differences in Reynolds number had little influence on the following discussion.

Aerodynamic data

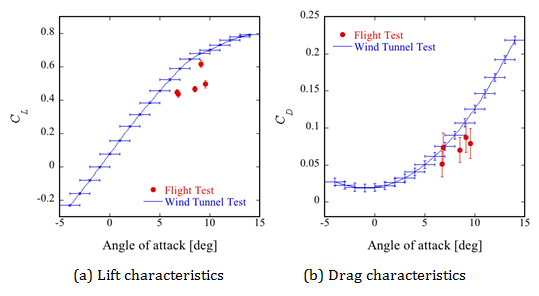
The aerodynamic data for the flight test at $Re=33,000\pm 10,000$ and $Re=77,000\pm 10,000$  are plotted in Figure 7 & 8, respectively, and compared with the wind tunnel data. The error bars indicate a three-sigma standard deviation based on the error analysis. As described above, the aerodynamic data in a relatively wide range of was plotted in Figure 7 & 8 because the aerodynamic performance of the Ishii airfoil has a low Reynolds number dependency on its lift curves at Re greater than 33,000 and remains about the same in the Reynolds number range of about $\pm 10,000$ . Also, since the Mach number in the vicinity of Re = 33,000 becomes M = 0.23-0.33, it is considered that the compressibility effect of the flow on the aerodynamic performance has little influence.

In Figure 7, there are 13 plots in the range of Re = 23,000-43,000, which correspond to the flight history at 9-13 s during the roll-control phase. During this period, an oscillation in the pitch of the airplane was observed in the angle of attack $(\alpha )$  that ranged from $4.2to12.9°$ . In addition, the angles of each control surface were also varied. The angle of the elevator $({\delta }_e)$ was fixed at $-13.5°$ , while those of the aileron $({\delta }_a)$ and rudder $({\delta }_r)$ were varied from $0.06to5.8°$  and from $4.6to6.3°$ , respectively. In reality, we have not performed the wind-tunnel tests under the same conditions that accurately corresponded to the deflection of each control surface and the Reynolds number in the actual flight test. Hence, the interpolated wind-tunnel data were plotted in Figure 7 using the data at ${\delta }_e=-10$  and -20° when ${\delta }_a$  and ${\delta }_r$  were fixed at 0°.

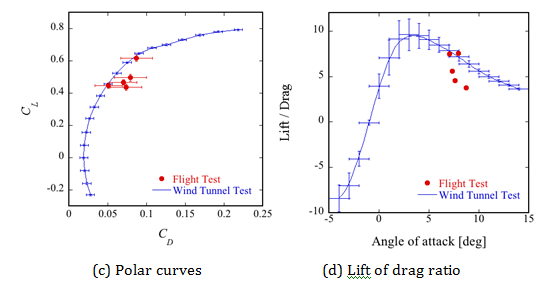
Although a moderate variation in the lift coefficients (CL) in the flight test can be seen in Figure 7a, the trend reflected by the CL change against $\alpha$  was similar to the results of the wind-tunnel test. However, quantitatively compared to the wind-tunnel data, the differences between both results were about 30%. A variation in the drag coefficients (CD) was also observed as shown in Figure 7b, and the errors were much larger than those found in CL. This large error in the CD measurement was due to the accuracy of the acceleration sensor. The acceleration sensors for Ax and Az have the same measurement accuracy (0.2 m/s2) and measurement range. Next, we selected the measurement range suitable for measuring the lift under a relatively large magnitude of force. The range of measured values of Ax and Az at $Re=33,000\pm 10,000$  were 0.13-0.73 m/s2 and 1.9-7.2 m/s2, respectively. This means the measurement accuracy of lift could be somewhat maintained, although the accuracy of drag decreased. Since it is difficult to accurately measure the drag force at such low Reynolds numbers, the main target of the aerodynamic measurement in this flight test was originally the lift force. The drag coefficients were similar to the results of the wind-tunnel test. There are concerns that these differences between the flight test and wind-tunnel test were affected by the measurement error of $\alpha$  To preclude this effect in this discussion, a polar curve was calculated and is shown in Figure 7c. However, the curve also shows a variation in almost all plots. It is difficult to conclude that the cause of the difference observed in the lift curve and drag curve is based on the effect of the angle of attack, because the low measurement accuracy of the drag also had an effect on the variation displayed in Figure 7c. The L/D shown in Figure 7d in the flight test is comparable in magnitude to the results of the wind-tunnel test. In a strict sense, L/D in the flight test is minimized by the effect of lower lift in the flight test versus the wind-tunnel test.

Figure 6: Flight histories of Reynolds number and Mach number.

The aerodynamic data in the flight test at $Re=70,000\pm 10,000$  were compared to the results obtained in the wind-tunnel test at Re = 70,000, as shown in Figure 8. There are five plots in the range Re = 60,000-80,000, which correspond to the flight history from 20.6 to 23.0 s for the pull-up phase. In this period, ${\delta }_e$  was maintained at -13.5°, and ${\delta }_a$ and ${\delta }_r$ were slightly varied from -0.17 to 0.5° and from 1.5 to 2.0°, respectively. Besides, $\alpha$ was varied from 6.7 to 9.6°. These deflections of the control surfaces were much smaller than those at Re = 33,000. As with the case for Re = 33,000, the interpolated wind-tunnel data using the data at ${\delta }_e=-10$ and -20° are plotted in Figure 8 as a comparison. Compared to the case at Re = 33,000, the measurement accuracy, especially for the drag curve, is much improved due to the increase of the dynamic pressure and the values of both Ax and Az.

A trend similar to the situation at Re = 33,000 is shown in Figure 7a, where a lower CL in the flight test is shown in Figure 8a. The difference in CL between the two tests was about 25%, which is less than the result for Re = 33,000. One possibility for this is the effect of compressibility on the aerodynamic performance since the Mach number reached about 0.58 at around Re = 70,000. Anyoji et al. [13] experimentally investigated the compressibility effects on lift performance at Re = 10,000 using the NACA0012-34 airfoil. Their results indicated that the compressibility decreased lift (from about 20 to 30%) at high angles of attack near the point of stall, while it did not affect lift curves at low angles of attack. The stall angle of the main wing at Re = 70,000 would be slightly higher than 8°, which corresponds to the stall angle of the Ishii airfoil at Re = 23,000. However, in Figure 8a, a lift decrease is commonly seen not only at angles of attack of more than 8° but also at  below the stall. These results and the other factors for lower lift in the flight test should be considered, but the former assertion should not be dismissed. In the drag curve shown in Figure 8b, the plotted data were close to or slightly lower than the results observed in the wind-tunnel test. The polar curve shown in Figure 8c exhibited good agreement with the data from the wind-tunnel test. The L/D shown in Figure 8d agreed well with that in the wind-tunnel test since both the lift and drag coefficients were lower than those in the wind-tunnel test.

Figure 7: Aerodynamic characteristics at $Re=33,000\pm 10,000$ compared to wind tunnel test results at Re = 33,000.

Figure 8: Aerodynamic characteristics of the Mars airplane flight at $Re=70,000\pm 10,000$ compared with the results for the wind-tunnel test at Re = 70,000.

Discussion of the difference between flight test results and wind-tunnel results

In this section, we discuss the difference between the flight test data and the wind-tunnel data as shown in Figure 7 & 8, particularly for the lift curve. The lift coefficients in the flight test at Re = 33,000 and 70,000 were 25 to 30% lower than those for the wind-tunnel data. One possible reason for this is the aeroelastic deformation. The aeroelastic deformation of this Mars airplane was initially investigated using JAXA’s 6.5 m 5.5 m low-speed wind tunnel under similar dynamic pressure conditions (approximately 65 Pa) employing a motion capture technique. The measured difference in $\alpha$  was found to be only 0.4° in the washout direction at $\alpha$ ranging from 5 to 10°. This means that the $\alpha$ variation was estimated to be about -0.4°. Since the deformation measurement using the motion capture technique could not be conducted at a dynamic pressure of 200 Pa, the deformation effect cannot be analyzed quantitatively but can be sufficiently considered. We deduced that the amount of deformation in the aircraft would be greater than that at a dynamic pressure of 65 Pa. In addition, the alignment error was also considered. Of course, a mounting adjustment was conducted before the flight test. However, in the laser evaluation of the mounting angle error, an installation error of the main wing might have occurred, which amounted to about -0.5°. Furthermore, considering each measurement error and a slight deformation of the Pitot tube during the flight, it was considered likely that $\alpha$ changed from about -0.5 to -1.0°. Considering these results, the total $\alpha$ error can be roughly estimated to be -1.5° or -2.0° as a stack of small $\alpha$ errors. Based on this result, if the $\alpha$ in the flight test is corrected for -1.5° or -2.0°, the aerodynamic data shown in Figure 7 & 8 would agree well with the wind-tunnel test results.

The possibility of the effect of the difference in ${\delta }_a$  between the flight test data and the wind-tunnel data was also considered. However, there was an approximately 30% difference in CL at $\alpha =10.4°$ , as shown in Figure 7a, even when ${\delta }_a$  was only 0.06°. Therefore, the difference in ${\delta }_a$  is limited in determining the variations in aerodynamic data.

The results of the investigation of the possible system factors indicated that an $\alpha$  error is the most likely reasonable cause of variations between the flight test data and the wind-tunnel data in the performance of the proposed Mars airplane. In designing and manufacturing the airplane used for MABA-2, we believe that it is essential to improve the factors that affect the $\alpha$ error.

In this study, we conducted a high-altitude flight test of our Mars airplane (MABE-1) design at 36 km altitude using an actual-scale Mars airplane and successfully obtained aerodynamic data in the roll-control and pull-up phases.

 As results of comparisons between the aerodynamic data obtained from the flight test and wind-tunnel experiments, a common trend was observed at Re = 33,000 and 70,000, where both lift and drag coefficients were lower than those observed in the wind-tunnel test. In particular, the lift coefficients were about 25-30% less than those found in the wind-tunnel tests. As a result of investigating various factors, it was concluded that the $\alpha$ error is the most likely reasonable cause of variation in the two datasets and it is essential to improve the factors that affect the $\alpha$ error. Correcting $\alpha$ , a good correlation with the wind tunnel data is obtained, and these results provide designing and manufacturing guidelines of the airplane for MABE-2.

The scientific balloon (DAIKIKYU) flight opportunity was provided by ISAS, JAXA. We would like to express our sincere thanks to all the staff of DAIKIKYU research and operation group and all members of the working group of the Mars airplane.

None.