Knowledge of population dynamics and its repercussions on health-required complex, long and expensive field studies. Big data tools are nowadays postulated as a tool of first magnitude for weighted population changes observed in real time if reliable sources of collection and adequate mathematical and computer tools for their assessment are available.

Main objective: Carry out a methodological approach to the use of big data applications to prepare auxological growth tables in our population with high statistical power. Assess how our population is in the auxological variables with respect to current standards in the country: Orbegozo 2011 and Spanish growth studies 2010.

Material and methods: Data collected from episodes of computerized medical records, studying the variables sex, age, weight, height, place of residence (PC, health center, neighborhood) of our population between 01/01/2020-03/31/2020 (avoiding effect pandemic). To calculate the curves and percentile tables we have used the Cole-Green LMS algorithm with penalized likelihood, implemented in the RefCurv 0.4.2 (2020) software, which allows managing large amounts of data. The hyperparameters have been selected using the BIC (Bayesian information criterion). To calculate population deviations from the reference, being above 1.5 standard deviations from the mean according to age has been taken as a reference.

Results: 66,975 computerized episodes of children under 16 years of age and a total of 1,205,000 variables studied are collected. Although data is available, individuals >16ª are excluded due to low N. The graphs of our population are represented with respect to the standards, observing that there are differences with Orbegozo 2011 and Spain 2010. We present the data and percentages of overweight/obesity by age and sex. There are significant differences of more overweight in the entire sample of men and women in our population than the usual standards.

Conclusion: Big data technology surpasses classic population studies in power and is an innovative tool compared to auxological studies (limited in N) carried out to date. The development of these new strategies in auxology will allow us to know almost in real time the epidemiological situation of the population in different variables, being able to infer health actions in a more effective way.

Note: CEIC OSI ARABA Approval Expte 2022-058

The study of human growth is defined as the process by which individuals increase their mass and height as they reach maturity, acquiring the functional characteristics of the adult state.¹ It is, therefore, considered a relevant indicator of health status in childhood. It is common clinical practice to weigh and measure children throughout the so-called growth.² Growth is not only the expression of a genetic capacity, but it is the phenotypic expression of the state of physical, mental and social well-being. In short, your health.³

To capture the situation of a minor in relation to individuals of the same age and sex, various growth curves have been developed, both at an international level (such as the classic ones by Tanner that are no longer in use), as well as others of a multinational nature or intention, such as those carried out by the WHO,^4,5 and which have been postulated as references for nutritional and general health status; as well as at the national level (in our country the one developed by Carrascosa⁶ - Spanish studies 2010 stands out) and at the regional level (In Euskadi, those developed by the Orbegozo Foundation in 1988, 2004 and 2011), as closest representatives of the reality of our environment.^6,7 These studies, if they are carried out of quality, are longitudinal in nature, so their very nature makes them long, expensive and with a limited number of subjects.

Current electronic medical records include, within normal clinical practice, the collection of multiple objective data, variables and clinical and medical-analytical constants. Among them, aspects of children's somatometry. Different statistical techniques, such as machine learning, would allow this data to be exploited, from a large number of cases (representatives of the majority of the population) in a semi-automated way and almost in real time. However, it is important that prior to analyzing the data, a purification of the data is carried out. This is because the information collected in medical records is for health care purposes; therefore, they are not generated for research purposes, so there may be variability or errors in measurement and transcription of the data.

To date, the production of growth charts was slow, lengthy, time-consuming and expensive. The question is why not take advantage of all the potential offered by medical databases and the use of big data? Another important element is the impact that the COVID-19 confinement may have had on the physical health of children. Although there are international studies on the matter (Pediatrics 2020, Children 2021),^8,9 there are no studies, at least in our environment and nearby population, regarding how the pandemic has been able to influence the weight/height relationship situation of childhood.

The existing studies to date on the somatometric situation of the child population, which are considered as a reference for our children, are based on cross-sectional or longitudinal designs with a small sample size.^4–7 This work is presented as an opportunity to use the data already existing on the computerized network to know first-hand the somatometric situation of our environment in minors.

Main objective: To describe the growth situation of the pediatric population in our area, Alava, Basque Country, Spain, by extracting variables from the electronic medical record and their subsequent analysis using a new big data approach. Check if these results obtained, current and from a large population (our study), differ significantly (expressed in SDS) for the different variables collected with respect to the normality established by the current studies of child auxology (Orbegozo 2011) (old and limited in size) through a comparison of paired means.

Design: It is a cross-sectional population study.

Study population: All children under 18 years of age under follow-up in the Basque health system, OSAKIDETZA, who present weight and height records in the OSABIDE GLOBAL tool in the Alava area.

Inclusion criteria:

1. Both sexes
2. Ages between 0 and 18 years
3. Be registered or present a registration address (according to GLOBAL data for the Alava/Araba area) belonging to the OSI Araba (which includes the entire rural area of the province except the LLODIO tax area) belonging to one of the centers of health of the OSI itself, collecting what it is in each case.
4. Have this data collected in the OSABIDE GLOBAL

Exclusion criteria: Not having data registered in GLOBAL

Sample size calculation: The study will include all people between 0 and 18 years old who reside in the historical territory of Araba (except as described). According to data from the Basque Institute of Statistics (Eustat), in 2021 there were 47,853 people between 0-19 years of age in Vitoria (Basque Institute of Statistics (Eustat). Population of the AC of Euskadi by territorial area, large age groups, sex and period. Available at: https://www.eustat.eus/bankupx/pxweb/es/DB/-PX_010154_cepv1_ep06b.px/table/tableViewLayout1/(Accessed 8/29/2022 ). Araba de Vitoria pediatric population, it is considered that it is not necessary to calculate the sample size. However, it is possible that after the data purification process there will be a loss in the number of participating subjects, in those cases where. those that have not recorded the data necessary to carry out the study or are not well recorded . To eliminate the effect of confinement (COVID-19) experienced by the population, or at least minimize it, the data to be studied would be those collected in the database with two different dates. This original article presents the data referring to all the records of the first quarter of the year 2022 existing in the database.

Variables

1. Main variables:
2. Weight (kg)
3. Size (cm)
4. Sex (Male, Female, Binary)
5. Age (expressed in years and months)
6. Registration date

Data management plan

A data protection impact assessment has been prepared. The OSI Araba IT service, the principal investigator of the project and the collaborating researchers will participate in the data life cycle, including professionals from the Basque Center for Applied Mathematics (BCAM) who are part of the research team. There is a collaboration agreement between the BCAM and the Bio araba Health Research Institute. The principal investigator requests the extraction of data (date of birth in month and year format, sex, weight, height, date of registration and health center) from the electronic medical record (EHR) to the OSI Araba IT service. The BCAM has the data obtained from Osakidetza's electronic medical records for the time necessary to carry out the following actions:

• Data purging
• Statistical analysis of data

Once the investigation is completed, said database will be completely destroyed by all people involved in this study.

Specific security measures were adopted to prevent re-identification and access by unauthorized third parties. The database obtained from the IT Service comes with a patient ID that is neither the CIC, nor medical history number, nor any other data that can be used for patient re-identification. Only the IT Service will be aware of that ID.

Data life cycle

Figure 1

Statistical analysis

Hierarchical Dirichlet process mixture model

In the field of machine learning, Dirichlet processes (DP)¹⁰ are a family of stochastic processes whose realizations (the values they take) are probability distributions. DPs are used in Bayesian inference to describe prior knowledge about the distribution of random variables, that is, the probability that random variables are distributed according to a particular distribution.

The Dirichlet process is specified by a base distribution and a positive real number, called the concentration parameter. The base distribution is the expected value of the process. A DP establishes distributions around the base distribution. Although the base distribution is continuous, the distributions extracted from a DP are discrete. The concentration parameter controls the number of PD values: the realizations are discrete distributions with decreasing concentration as the concentration parameter increases.

The Dirichlet process can also be seen as the generalization in infinite dimensions of the Dirichlet distribution. In the same way as the conjugate Dirichlet distribution for the categorical distribution, the Dirichlet process is the conjugate for infinitely many discrete non-parametric distributions. A particularly important application of Dirichlet processes is as a priori probability distribution in infinite mixture models.¹¹

In this project we will adopt this approach, and the DP will allow us to build Gaussian-averaged models (GM).¹¹ These models are known as Gaussian averaging models based on Dirichlet processes (Dirichlet process Gaussian mixture models, DPGMM).

DPGMMs are especially of interest for modeling populations in which the number of groups (clusters) is unknown, because they are capable of establishing the number of components and their parameters (means and covariance matrices) of the Gaussian averaging model. Automatically. The number of components will be determined by the data and by the value of the concentration parameter. The DPGMM will allow solving two problems simultaneously: performing a probabilistic segmentation (clustering) of the study population and at the same time modeling its underlying distribution (density estimation) in terms of GMs.

The DPGMM will allow the study population to be analyzed, a new individual to be classified into one of the previously identified groups, and predictions to be made about the variables that characterize it. However, the objective of this study is to analyze different populations that can be segmented according to different criteria, eg, location or age. To do this, we will need to add a higher level of abstraction to the DPs.

A hierarchical Dirichlet process (HDP) is a non-parametric Bayesian approach to data clustering.¹¹ HDP employs one DP for each of the populations, subject to the constraint that all DPs share a base distribution. This base distribution is drawn from a DP higher in the hierarchy, and hence the term hierarchical Dirichlet process. In terms of the DPGMM, the DPs of each of the populations share the Gaussian components and the highest DP in the hierarchy groups the DPGMM of the populations and in turn establishes the strength of each Gaussian component. In this way, HDPs allow groups to share statistical strength by exchanging clusters between groups, and in turn cluster the different populations. Again, in HDPs the number of GM components, the number of population clusters and the weights of the GM components are set automatically from the data.

Application to the study of populations

In this project, we will address the analysis of a set of populations using Gaussian averaging models based on hierarchical Dirichlet processes (Hierarchical Dirichlet process Gaussian mixture model, HDPGMM).¹² This will allow us to address the following problems: 1) learn a GM model for the set of populations, 2) establish the different clusters of individuals with differentiated behavior within the total population, 3) establish clusters of populations with similar behavior, 4 ) determine the strength of the components of the GM in each population, 5) classify a new individual in one of the components of the GM and infer the value of some of its variables from the value of the rest, and 6) compare the results obtained at two time points and analyze the evolution of the populations.

Specifically, by grouping the data according to the different variables, clusters will be obtained that will inform us about the somatometric similarities and differences of the population depending on the date of data collection, age, sex, or health center.¹³ In this way, in addition to being able to draw conclusions about the general population (secondary objectives 1 and 3), secondary objectives 2 and 5 can also be attacked. The study will also be an opportunity to study and incorporate recent methodological innovations on similar databases to ours.^14–16

Because the problems of clustering and density estimation are solved in learning HDPGMM, the results can be visualized intuitively using standard visualization techniques such as linear projections to 2D spaces, eg, Distributed Stochastic Neighbor Embedding (DSNE). ) and Multidimensional Scaling (MDS). Throughout the process, open source Python libraries are used: Pandas for data management and preprocessing, Sklearn for the basic algorithms (DSNE, MDS) and Matplotlib for the visualization of the results. Regarding the HDPGMM model, we propose our own open source implementation based on public domain libraries such as https://github.com/blei-lab/online-hdp .We proceed from each studied variable to carry out MEDIAS and SDS studies. Likewise, these data are compared with the means and SDS of the studies published to date and references of our population (Orbegozo 2004, 2011 and Españolas 2011).

Data has been obtained from a total of 67,270 minors. The sum of all the variables studied (24 per case) given the number of cases represents 1,749,020 variables. Although data is available for the age range of 16-18 years, the number of available data being scarcer and with the dispersion presented, it was advised by the collaborative study team, to avoid bias, to be eliminated from this presentation. We present in various tables the results obtained by sex, age and the variables WEIGHT, HEIGHT and BMI (Table 1-3).

This variable is represented using graphs in percentile format (Chart 1–3).

Chart 1 Representation percentiled by age of the variable WEIGHT (Kgrs). Abscissa age in months.

Chart 2 Percentile representation by age of the SIZE variable (cms). Abscissa age in months.

Chart 3 Percentile representation by age of the BMI variable (Kgs/m2). Abscissa age in months.

Next, we proceed to study using the so-called Hierarchical Dirichlet process Gaussian mixture model or method, applied to our population (big data study 2022) vs. reference graphs most used to date in the region (Orbegozo 2011) and the largest study in number of cases, most recent (Spanish study 2010) and used in the country. It will be assessed if there are differences at a significance of p<0.05.

We represent the differences between our study (in black) and the referenced population (in red) of each of the studies and variables using the mean +/- 2 SDS (Chart 4–9).

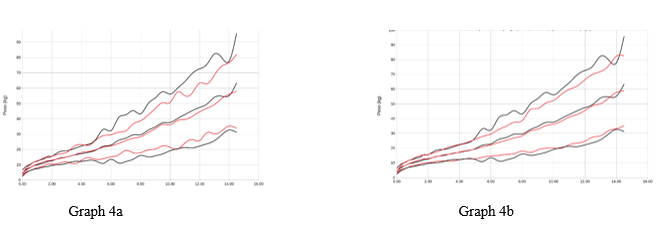
Chart 4 Representation of men average +/- 2sds by age (years) of the variable weight (kgs). Reference study in red, our population in black. Graph 4a with respect to orbegozo, Graph 4b with respect to Españolas.

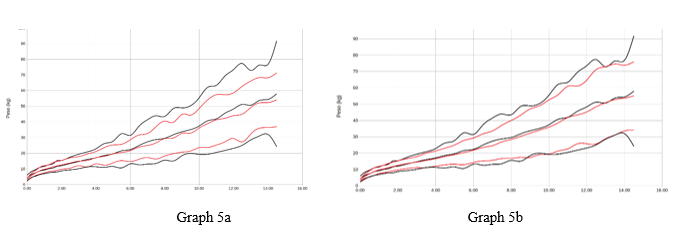
Chart 5 Representation of women average +/- 2 sds by age (years) of the variable weight (kgs). Reference study in red, our population in black. Graph 5a with respect to orbegozo, Graph 5b with respect to Españolas.

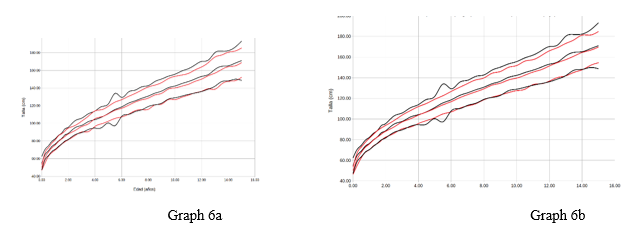
Chart 6 Representation of men average +/- 2 sds by age (years) of the variable size (cms). Reference study in red, our population in black. Graph 6a with respect to orbegozo, Graph 6b with respect to Españolas.

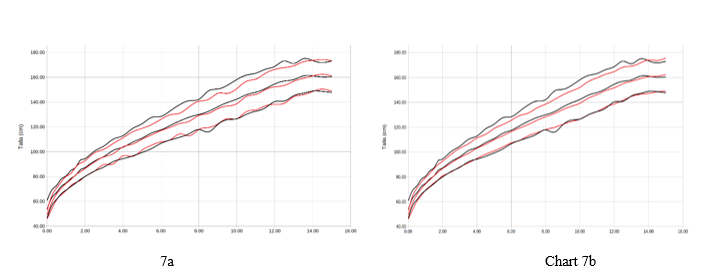
Graph 7 Representation of women average +/- 2 sds by age (years) of the variable size (cms). reference study in red, our population in black. Graph 7a with respect to orbegozo, Graph 7b with respect to Españolas.

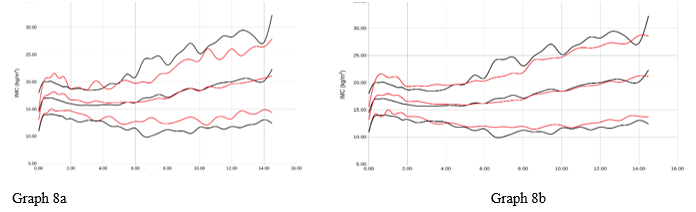
Graph 8 Representation of men average +/- 2 sds by age (years) of the bmi variable (kgr/m2). Reference study in red, our population in black. Graph 8a with respect to orbegozo, Graph 8b with respect to Españolas.

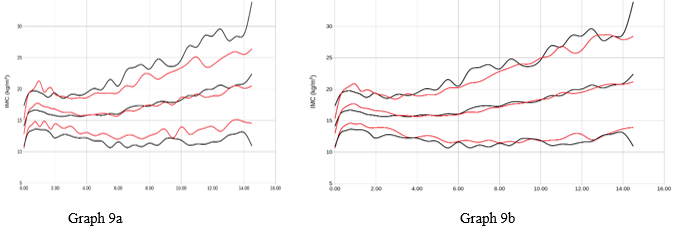
Graph 9 Representation of women AVERAGE +/- 2 SDS by age (years) of the BMI variable (Kgr/m²). Reference study in red, our population in black. Graph 9a with respect to ORBEGOZO, graph 9b with respect to Españolas.

The curves have not been smoothed using a statistical method so that they reflect the reality of the observed sample. A significant difference is evident in each of the weight and height variables and for all ages (p<0.05) in comparison between our study and reference studies. The population studied is generally taller and heavier than the reference population using the Hierarchical Dirichlet process Gaussian mixture model method (Table 4).

We represent here the data referring to BMI in a table as an example of the method used. The differences observed are smaller than in other variables because the differences in weight are compensated by the greater height of the subjects analyzed. Even so, it is observed that the weight variable is higher than the height variable in our population than the referenced population, which contributes to the degree of overweight expressed in the form of BMI also being higher.

The somatometric assessment of a child in relation to individuals of the same age and sex to date, whether cross-sectional or semi-longitudinal studies, of a regional, national or international nature, are used, but almost always with a number of cases limited by the complexity of the technique and the cost of their development^4,5 However, its importance is vital to have a tool for comparison and assessment of children's health and which have been postulated as references for nutritional and general health status; as well as at the national level (in our country the one developed by Carrascosa⁶ stands out – Spanish studies 2010) and at the regional level (In Euskadi, those developed by the Orbegozo Foundation in 1988, 2004 and 2011).^6,7 These studies, if they are carried out of quality, are longitudinal in nature, so their very nature makes them long, expensive and with a limited number of subjects.

Current electronic medical records include the collection of multiple data and clinical constants as part of normal clinical practice. Among them, aspects of children's somatometry. Different statistical techniques, such as machine learning, have been demonstrated in other fields^14–16 to be effective in interpreting a large amount of data generated in real life and being able to make decisions about it. We postulate with works like ours the possibility of real use of this technology to obtain updated growth graphs and almost in real time of such a number of individuals that makes the power of the studies very significant.

In this work we present this possibility made reality as a methodological approach. Although data is available for the age range of 16-18 years, the smaller number of cases in relation to the other ages and their dispersion, requires that they be eliminated through the statistical procedure of the study and to avoid biases of this study. This is because adolescents go to the doctor less and therefore the number of registrations is lower. To assess adolescent populations, we postulate the possibility of carrying out ad hoc studies of this population, using databases from educational and sports centers...

The differences with Orbegozo and the Spanish State in the cases of Height, Weight and BMI are statistically significant with respect to our population in 2022. The secular acceleration of weight and height^4,5 is seen in our population since this, ours, is on average 10 years later chronologically 2010 vs 2022.

Of all the variables, the one that most affects this comparative acceleration is BMI. This is revealed in the study and may be due to various causes, such as the childhood obesity pandemic that we are experiencing, the effect of confinement/COVID-19 (8-9) in 2022 on children's health, changes in food or even the typology of the area's population (immigration rate, socioeconomic level).^2–4 In this work, the child population has been affected by the COVID-19 pandemic. This fact could be a negative bias in population studies. It is known that confinement or even the disease itself ¹⁷ (it has been postulated in immunological changes, and in the expression of various active genes that could influence the henotypic changes that have occurred in various people after the primo-infection) could have played a role. a relevant role in the population changes that occur after 2021.

This study method with BIG DATA is postulated as a faster and more economical way to have updated regional graphs than classic studies. This point should be verified with other studies. Likewise, we add that the problem with percentile curves is that they are obtained from a normalization and adjustment method called LMS; Orbegozo and Española presents these tabulated results.^6,7 Likewise, empirical graphs were used that are obtained directly from the means and standard deviations. The authors encourage work in this sense and this work is the basis for developing community intervention strategies pending corroboration by our own team.

The main limitation of the study has to do with the fact that the data to be used comes from the electronic medical record and therefore has not been generated for research purposes. This is why, as described in the literature, errors may occur in the measurement and transcription of the data.³ A big-data approach to producing descriptive anthropometric references: a feasibility and validation study of pediatric growth charts as is referred on Lancet Digit Health. 2019 Dec;1(8):e413-e423). To minimize this limitation, data extracted from elecThe main limitation of the study has to do with the fact that the data to be used comes from the electronic medical record and therefore has not been generated for research purposes. This is why, as described in the literature, errors may occur in the measurement and transcription of the data.3 A big-data approach to producing descriptive anthropometric references: a feasibility and validation study of pediatric growth charts as is referred on Lancet Digit Health. 2019 Dec;1(8):e413-e423). To minimize this limitation, data extracted from electronic medical records will be cleaned before proceeding with the statistical analysis of the data.tronic medical records will be cleaned before proceeding with the statistical analysis of the data.

The expected impact of the project results, in terms of the capacity for modification in healthcare processes, to improve the health and quality of life of patients is of great importance. It is estimated that the current cost of preparing an updated, regional, longitudinal growth study, with the consequent limit of cases (<1,000) is more than 8-10 years per project and with an economic cost greater than 60,000 euros in said period, taking into account takes into account published studies (Orbegozo) in its methodology. This project has been developed in a much shorter time and at a lower cost

Furthermore, the data obtained is not limited to a limited population (although it is supposed to be representative) but rather quasi-real as it encompasses most of the data available on the computer servers in the area. The nature of this study allows it to be repeated periodically, detecting areas of improvement in different subpopulations. On the other hand, by having variables associated with the growth of another type such as a health center, it will allow detecting areas of socio-health risk, where to implement other types of studies or intervention measures...

The study has been prepared respecting the principles established in the Declaration of     (1964), latest version Fortaleza, Brazil 2013, in the Council of Europe Convention on Human Rights and Biomedicine (1997), and in the regulations on biomedical research. , protection of personal data. Law 14/2007 on Biomedical Research Study approved by the CEIC on 03/24/2023 with CODE Expte 2022-058

The study will be carried out without funding. The tasks described in the project are assumed by the main researcher and his collaborators.

This original study has been support thanks to the work of the Collaborative Group from Basque Centre of Applied Mathematics (BCAM). Bilbao, Bizkaia Basque Country, Spain

1. Jose A. Lozano Basque Center for Applied Mathematics BCAM
2. Ioar Casado Tellechea Basque Center for Applied Mathematics BCAM
3. Aritz Pérez Postdoctor Fellow BCAM - Basque Center for Applied Mathematics
4. Mónica Machón Sobrado Methodology and Statistics unit OSI Araba, Collaborative Group from Basque Center of Applied Mathematics (BCAM), Spain

1. Zamlout A, Kamal Alwannous, Ali K, et al. Syrian national growth references for children and adolescents aged 2-20 years. BMC Pediatr. 2022;22(1):282.
2. Tarupi W, Yvan L, María LF, et al. Growth references for weight, height, and body mass index for Ecuadorian children and adolescents aged 5-19 years. Arch Argent Pediatr. 2020;118(2):117–124.
3. Heude B, Pauline Scherdel, Andreas Werner, et al. A big-data approach to producing descriptive anthropometric references: a feasibility and validation study of pediatric growth charts. Lancet Digit Health. 2019;1(8):e413–e423.
4. WHO Multicenter Growth Reference Study Group. WHO child growth standards based on length/height, weight and age. Acta Paediatr Suppl. 2006;450:76–85.
5. Onis M, Adelheid WO, Elaine B et al. Development of a WHO growth reference for school-aged children and adolescents. Bull World Health Organ. 2007;85(9):660–667.
6. Carrascosa LA, Fernandez Garcia JM, Fernandez R, et al. [Spanish cross-sectional growth study 2008. Part II: height, weight and body mass index values from birth to adulthood]. An Pediatr (Barc). 2008;68(6):552–569.
7. Sánchez GE, Carrascosa L, Fernandez Garcia JM et al. [Spanish growth studies: current situation, usefulness and recommendations for their use]. An Pediatr (Barc). 2011;74(3):193.e1–16.
8. Loucia A, Will C, Christine J. The indirect impact of covid-19 on child health. Paediatr and Child Health(Oxford). 2020;30(12):430–437.
9. Stavridou A, Kapsali E, Panagouli E, et al. Obesity in children and adolescents during covid-19 pandemic. Children. 2021;8(2):135.
10. Ferguson TS. A Bayesian analysis of some nonparametric problems. Ann. statist. 1973;1(2):209–230.
11. Rasmussen C. The infinite gaussian mixture model. MIT Press. 2000;554–560.
12. The YW, Jordan MI. Hierarchical bayesian nonparametric models with applications. Bayesian nonparametrics. 2009;1:158-207.
13. Van der ML, Hinton G. Visualizing data using t-SNE. Journal of machine learning research. 2008;9(11):2579–2605.
14. Kruskal JB. Non metric multidimensional scaling: a numerical method. Psychometrika. 1964;29(2):115–129.
15. Gilholm P, Mengersen K, Thompson H. Identifying latent subgroups of children with developmental delay using bayesian sequential updating and dirichlet process mixture modeling. PloS one. 2020:15(6):e0233542.
16. Diana A, Matechou E, Griffin J, et al. A hierarchical dependent dirichlet process prior for modeling bird migration patterns in the uk. The Annals of Applied Statistics. 2020;(1):473–493.
17. Ian James Martins. COVID-19 infection and anti-aging gene inactivation. Acta Scientific Nutritional Health. 2020;4(5):01–02.