Control charts are considered as important tools when producer wants to produce goods or services of high–quality. These charts help producers to manufacture products based on specified limits by monitoring the quality beforehand.1 There are a number of control charts developed to monitor production process in different situations. One of the major characteristics of many control charts is that the production process should follow normal distribution. Ouyang et al.2 and Pearn and Wu3 they mentioned efficiency of process capability (PC) based on the production process which follows normally distributed processes. According to Aslam and Jun1 there are also other control charts which are developed based on non–normal distributions which are being used when the production process follows other distributions rather than normal. Rao4 developed a control chart for time truncated life tests using exponentiated half logistic distribution and Rao et al.5 constructed attribute control charts for the Dagum distribution under truncated life tests.
If a quality characteristics of the production process does not follow normal distribution and the experimenter developed a control chart based on the assumption that it follows normal distribution, it will led to a wrong result. A number of non–normal control chart have being developed by Al–Oraini and Rahim.,6; Amin et al.,7; Lin and Chou., 8; McCracken and Chakraborti,9; Ahmad et al.,10). On the other hand control charts are divided into variables or measurements and attributes.11 Control charts for variables monitor characteristics that can be measured and have a continuous scale whereas control charts for attributes are used to measure quality characteristics that are counted rather than measured, such as a fraction defective or nonconformities per unit of product.
One among control charts for attributes include np chart based on the study conducted by Rodrigues et al.12 and Epprecht et al.13 considered usual Shewhart np control charts are used for monitoring the number of non–conforming products rather than proportion as in p–charts. Several authors have conducted studies on how control charts for attributes are being used in several situations such as Epprecht et al.,13 Costa and Rahim,14 Hsu15,16, Wu et al.,17 Wu and Wang18 and Barbosa and Joekes.19 In a study conducted by Kantam and Rosaiah20 suggested sampling plan on life tests while the failure density model is half logistic distribution. Furthermore Kantam et al.21 considered acceptance sampling mainly on life tests while the failure density model of the products was a log–logistic distribution. It is also noted that Kantam et al.22 studied an economic reliability test plan using log–logistic distribution.
Based on the literature review made, it is noted that there is no study on log–logistic distribution based on truncated life tests. In this study we have developed attribute control chart of log–logistic distribution by incorporating the truncated life test.
Assume the failure time of a product follows a log logistic distribution in which its cumulative distribution function (cdf) is
(1)
whereas the pdf is given by
(2)
where
is the shape parameter. The mean life of a product for a log–logistic distribution is given as:
(3)
Let
be the center mean life when the production process is in control. The aim is to design a control chart for monitoring shift from center line by counting the number of failed items in a specified truncated time
. The probability that a product fails by time
is given by
(4)
By specifying the truncation time
using a multiple in–control process mean in the cause of
where a is constant (termed as a truncated time constant) then the equation (4) above can be rewritten as
(5)
where
and hence
with
.
We have therefore proposed np control chart for a log–logistic distribution based on the number of failed items for each subgroup:
Step 1: Taking a sample of size
from a certain production process. If we count the number of failures by considering the specified time
whereby
is a constant and
is the target mean when the production process is in control.
Step 2: Conclude the process is out of control when
or
and the production process said to in control when
.
It should be noted that the above chart is
chart because number of failures has being used instead of proportion of failures. When the production process is in control the random variable
follows a binomial distribution with parameters
and
. Thus the upper and lower control limits for the suggested
chart will be:
(6a)
(6b)
Where
is the control constant or coefficient of the control limits to be determined. The probability
should be estimated when the process is in control from a preliminary sample, since its unknown. Thus, the
and
limits to be used in practice will be:
(7a)
(7b)
Where
is the average number of failures in a batch or lot over a preliminary sample.
It should be noted that in this study we have considered control limits in the form of equation [6a&6b]. The aim is to investigate of the new control chart proposed by using average run length. The proportion that production process is declared to be in control when in fact it is real in control is given by
=
(8)
During evaluation of the sum above it should be noted that the value of
should be 0 if
. Average run length (ARL) is usually used to evaluate the performance of the control chart. When the process is in control ARL is always given by
.
(9)
ARL when scale parameter is shifted
The process is declared to be out–of–control when the process is shifted to a new scale parameter
, where c is a shift constant. In this case, the probability that an item is failed before the experiment time
denoted by p1, is obtained by
. (10)
It should be noted that mean
corresponds to the probability
while when the process is out of control mean
corresponds to the probability
. Therefore the probability that, the process is said to be in control when the mean has shifted to
is given by
(11)
and when the process is out of control ARL is given by
.
(12)
We used the following algorithm to complete the tables for the proposed control chart.
- Specify the values of ARL, say r0 and shape parameters
.
- Determine the values of control chart parameters and sample size n for which the ARL0 from Equation (9) is close to r0.
- Use the values of control chart parameters obtained in step 2 to find ARL1according to shift constant c using Equation (12).
We determined the control chart parameters and ARL1 for various values of
, r0 and n and placed in Tables 1–4.
|
|
1.5
|
2
|
2.5
|
3
|
|
n
|
25
|
25
|
26
|
26
|
|
LCL
|
9
|
9
|
5
|
7
|
|
UCL
|
22
|
22
|
19
|
21
|
|
a
|
0.6296
|
0.8727
|
0.7238
|
0.8845
|
|
L
|
2.8072
|
2.8175
|
2.8582
|
2.8815
|
|
c
|
ARL1
|
ARL1
|
ARL1
|
ARL1
|
|
1.00
|
200.01
|
200.05
|
200.03
|
200.03
|
|
0.95
|
188.09
|
174.69
|
157.04
|
174.87
|
|
0.90
|
140.55
|
109.30
|
73.46
|
72.63
|
|
0.85
|
92.64
|
61.31
|
31.91
|
28.49
|
|
0.80
|
58.48
|
34.27
|
14.69
|
12.34
|
|
0.75
|
36.71
|
19.69
|
7.37
|
6.04
|
|
0.70
|
23.26
|
11.75
|
4.09
|
3.37
|
|
0.65
|
14.97
|
7.31
|
2.52
|
2.14
|
|
0.60
|
9.83
|
4.76
|
1.74
|
1.54
|
|
0.55
|
6.61
|
3.26
|
1.34
|
1.24
|
|
0.50
|
4.56
|
2.36
|
1.14
|
1.10
|
|
0.40
|
2.40
|
1.45
|
1.01
|
1.01
|
|
0.30
|
1.48
|
1.12
|
1.00
|
1.00
|
|
0.20
|
1.11
|
1.02
|
1.00
|
1.00
|
|
0.10
|
1.01
|
1.00
|
1.00
|
1.00
|
Table 1 ARLs for the proposed chart for r0=200 when scale parameter is shifted
|
|
1.5
|
2
|
2.5
|
3
|
|
n
|
23
|
25
|
23
|
25
|
|
LCL
|
7
|
4
|
2
|
4
|
|
UCL
|
20
|
18
|
15
|
18
|
|
a
|
0.5723
|
0.5732
|
0.6126
|
0.7711
|
|
L
|
2.8991
|
2.8934
|
2.8183
|
2.8923
|
|
c
|
ARL1
|
ARL1
|
ARL1
|
ARL1
|
|
1.00
|
250.01
|
250.05
|
250.04
|
250.03
|
|
0.95
|
235.18
|
221.78
|
196.08
|
176.32
|
|
0.90
|
175.36
|
128.02
|
94.33
|
67.43
|
|
0.85
|
114.89
|
63.86
|
41.05
|
25.45
|
|
0.80
|
71.86
|
31.74
|
18.57
|
10.70
|
|
0.75
|
44.60
|
16.38
|
9.04
|
5.14
|
|
0.70
|
27.90
|
8.91
|
4.82
|
2.85
|
|
0.65
|
17.70
|
5.16
|
2.85
|
1.83
|
|
0.60
|
11.43
|
3.21
|
1.88
|
1.35
|
|
0.55
|
7.55
|
2.17
|
1.40
|
1.14
|
|
0.50
|
5.12
|
1.59
|
1.16
|
1.04
|
|
0.40
|
2.59
|
1.12
|
1.01
|
1.00
|
|
0.30
|
1.55
|
1.01
|
1.00
|
1.00
|
|
0.20
|
1.13
|
1.00
|
1.00
|
1.00
|
|
0.10
|
1.01
|
1.00
|
1.00
|
1.00
|
Table 2 ARLs for the proposed chart for r0=250 when scale parameter is shifted
|
|
1.5
|
2
|
2.5
|
3
|
|
n
|
28
|
24
|
27
|
24
|
|
LCL
|
8
|
4
|
6
|
4
|
|
UCL
|
23
|
18
|
21
|
18
|
|
a
|
0.5222
|
0.5979
|
0.7655
|
0.7931
|
|
L
|
2.9063
|
2.9645
|
2.9613
|
2.9635
|
|
c
|
ARL1
|
ARL1
|
ARL1
|
ARL1
|
|
1.00
|
300.00
|
300.04
|
300.02
|
300.02
|
|
0.95
|
228.91
|
268.57
|
281.24
|
214.41
|
|
0.90
|
144.20
|
156.30
|
131.34
|
82.71
|
|
0.85
|
84.94
|
78.36
|
53.82
|
31.28
|
|
0.80
|
49.58
|
39.02
|
23.25
|
13.08
|
|
0.75
|
29.27
|
20.10
|
10.95
|
6.19
|
|
0.70
|
17.64
|
10.86
|
5.69
|
3.35
|
|
0.65
|
10.90
|
6.22
|
3.29
|
2.09
|
|
0.60
|
6.94
|
3.81
|
2.13
|
1.49
|
|
0.55
|
4.58
|
2.51
|
1.54
|
1.20
|
|
0.50
|
3.15
|
1.79
|
1.24
|
1.07
|
|
0.40
|
1.73
|
1.18
|
1.03
|
1.00
|
|
0.30
|
1.19
|
1.02
|
1.00
|
1.00
|
|
0.20
|
1.02
|
1.00
|
1.00
|
1.00
|
|
0.10
|
1.00
|
1.00
|
1.00
|
1.00
|
Table 3 ARLs for the proposed chart for r0=300 when scale parameter is shifted
|
|
1.5
|
2
|
2.5
|
3
|
|
n
|
13
|
30
|
17
|
23
|
|
LCL
|
2
|
5
|
0
|
5
|
|
UCL
|
12
|
21
|
11
|
19
|
|
a
|
0.5651
|
0.5603
|
0.552
|
0.8671
|
|
L
|
2.8593
|
2.9793
|
2.9876
|
2.9981
|
|
c
|
ARL1
|
ARL1
|
ARL1
|
ARL1
|
|
1.00
|
370.03
|
370.05
|
370.00
|
370.05
|
|
0.95
|
314.20
|
323.07
|
316.82
|
329.65
|
|
0.90
|
240.56
|
166.74
|
175.21
|
136.60
|
|
0.85
|
173.40
|
74.71
|
82.38
|
52.22
|
|
0.80
|
121.40
|
33.99
|
38.34
|
21.69
|
|
0.75
|
83.98
|
16.31
|
18.53
|
10.02
|
|
0.70
|
57.90
|
8.37
|
9.48
|
5.20
|
|
0.65
|
39.94
|
4.66
|
5.21
|
3.04
|
|
0.60
|
27.64
|
2.84
|
3.11
|
2.01
|
|
0.55
|
19.22
|
1.91
|
2.05
|
1.49
|
|
0.50
|
13.45
|
1.43
|
1.50
|
1.22
|
|
0.40
|
6.76
|
1.06
|
1.08
|
1.03
|
|
0.30
|
3.57
|
1.00
|
1.00
|
1.00
|
|
0.20
|
2.03
|
1.00
|
1.00
|
1.00
|
|
0.10
|
1.29
|
1.00
|
1.00
|
1.00
|
Table 4 ARLs for the proposed chart for r0=370 when scale parameter is shifted
From these tables, we note that a rapidly decreasing trend in ARLs as the shift constant decreases. Same is observed for various parametric combinations that we considered in this article.
ARL when shape parameter is shifted
In this section, we will present the designing of the proposed chart when the shape is shifted due to some extraneous factors. Let us assume that the shape parameter is shifted to
for a shift constant
. In this case, the probability that an item is failed before the experiment time
, denoted by
, is obtained by
(13)
where
.
The probability of in control for the shifted process is given as follows:
(14)
The efficiency of the control chart is measured using the ARL. The ARL for the shifted process is given as follows:
(15)
We determined the control chart parameters and ARL2 for various values of
, r0 and n and placed in Tables 5–8.
|
n
|
36
|
21
|
26
|
17
|
18
|
|
LCL
|
12
|
5
|
9
|
5
|
6
|
|
UCL
|
29
|
18
|
23
|
16
|
17
|
|
a
|
0.7633
|
0.7253
|
0.8466
|
0.8787
|
0.9422
|
|
L
|
2.971
|
3.02
|
3.017
|
2.987
|
2.866
|
|
f
|
ARL1
|
ARL1
|
ARL1
|
ARL1
|
ARL1
|
|
1.0
|
300.05
|
300.03
|
300.05
|
300.02
|
300.00
|
|
1.1
|
144.00
|
148.18
|
153.29
|
171.87
|
200.53
|
|
1.2
|
53.97
|
59.03
|
75.19
|
99.86
|
127.77
|
|
1.3
|
24.26
|
30.12
|
41.38
|
62.82
|
85.67
|
|
1.4
|
12.83
|
17.33
|
25.26
|
42.47
|
60.98
|
|
1.5
|
7.69
|
10.95
|
16.72
|
30.41
|
45.65
|
|
1.6
|
5.08
|
7.45
|
11.79
|
22.78
|
35.59
|
|
1.7
|
3.63
|
5.38
|
8.74
|
17.69
|
28.65
|
|
1.8
|
2.76
|
4.09
|
6.74
|
14.14
|
23.68
|
|
1.9
|
2.21
|
3.24
|
5.38
|
11.57
|
19.98
|
|
2.0
|
1.85
|
2.66
|
4.41
|
9.67
|
17.16
|
|
2.5
|
1.16
|
1.44
|
2.20
|
4.84
|
9.58
|
|
3.0
|
1.02
|
1.12
|
1.49
|
3.04
|
6.38
|
|
3.5
|
1.00
|
1.03
|
1.21
|
2.18
|
4.70
|
Table 5 ARLs for the proposed chart for r0=300 when shape parameter is shifted when=2
|
n
|
31
|
24
|
24
|
35
|
18
|
|
LCL
|
1
|
1
|
4
|
10
|
3
|
|
UCL
|
15
|
14
|
18
|
27
|
15
|
|
a
|
0.5878
|
0.6459
|
0.8092
|
0.8872
|
0.8771
|
|
L
|
2.9290
|
2.8670
|
3.0190
|
2.9440
|
2.9370
|
|
f
|
ARL1
|
ARL1
|
ARL1
|
ARL1
|
ARL1
|
|
1.0
|
300.02
|
300.02
|
300.03
|
300.02
|
300.02
|
|
1.1
|
242.63
|
247.56
|
252.66
|
257.17
|
294.45
|
|
1.2
|
85.33
|
106.27
|
143.13
|
154.28
|
223.16
|
|
1.3
|
34.59
|
48.32
|
78.67
|
89.34
|
154.51
|
|
1.4
|
16.71
|
24.92
|
45.88
|
54.44
|
106.55
|
|
1.5
|
9.31
|
14.34
|
28.55
|
35.18
|
75.23
|
|
1.6
|
5.82
|
9.04
|
18.82
|
23.94
|
54.66
|
|
1.7
|
3.99
|
6.14
|
13.04
|
17.03
|
40.82
|
|
1.8
|
2.96
|
4.45
|
9.42
|
12.57
|
31.24
|
|
1.9
|
2.33
|
3.40
|
7.07
|
9.58
|
24.43
|
|
2.0
|
1.92
|
2.72
|
5.48
|
7.51
|
19.48
|
|
2.5
|
1.18
|
1.41
|
2.25
|
3.05
|
7.83
|
|
3.0
|
1.04
|
1.12
|
1.42
|
1.79
|
4.11
|
|
3.5
|
1.01
|
1.03
|
1.14
|
1.32
|
2.59
|
Table 6 ARLs for the proposed chart for r0=300 when shape parameter is shifted when=3
|
n
|
17
|
20
|
24
|
22
|
17
|
|
LCL
|
0
|
4
|
8
|
8
|
6
|
|
UCL
|
11
|
17
|
22
|
21
|
17
|
|
a
|
0.4291
|
0.6909
|
0.8438
|
0.9213
|
0.9867
|
|
L
|
3.4100
|
3.0580
|
3.0960
|
3.1400
|
3.1020
|
|
f
|
ARL1
|
ARL1
|
ARL1
|
ARL1
|
ARL1
|
|
1.0
|
370.00
|
370.05
|
370.01
|
370.03
|
370.04
|
|
1.1
|
157.05
|
157.01
|
157.87
|
178.64
|
202.24
|
|
1.2
|
59.85
|
66.56
|
76.70
|
98.85
|
127.82
|
|
1.3
|
27.73
|
32.80
|
42.70
|
61.36
|
89.08
|
|
1.4
|
15.06
|
18.34
|
26.37
|
41.48
|
66.52
|
|
1.5
|
9.23
|
11.32
|
17.61
|
29.88
|
52.26
|
|
1.6
|
6.22
|
7.57
|
12.50
|
22.59
|
42.65
|
|
1.7
|
4.51
|
5.39
|
9.30
|
17.73
|
35.85
|
|
1.8
|
3.48
|
4.05
|
7.20
|
14.34
|
30.85
|
|
1.9
|
2.80
|
3.18
|
5.75
|
11.88
|
27.05
|
|
2.0
|
2.35
|
2.60
|
4.72
|
10.05
|
24.08
|
|
2.5
|
1.41
|
1.40
|
2.34
|
5.32
|
15.72
|
|
3.0
|
1.15
|
1.11
|
1.57
|
3.47
|
11.91
|
|
3.5
|
1.06
|
1.03
|
1.25
|
2.55
|
9.75
|
Table 7 ARLs for the proposed chart for r0=370 when shape parameter is shifted when=2
|
n
|
42
|
30
|
29
|
34
|
35
|
|
LCL
|
3
|
5
|
7
|
10
|
12
|
|
UCL
|
20
|
21
|
23
|
27
|
29
|
|
a
|
0.5997
|
0.7595
|
0.8493
|
0.8982
|
0.9521
|
|
L
|
2.966
|
2.979
|
3.002
|
3.077
|
3.061
|
|
f
|
ARL1
|
ARL1
|
ARL1
|
ARL1
|
ARL1
|
|
1.0
|
370.03
|
370.04
|
370.01
|
370.04
|
370.03
|
|
1.1
|
183.21
|
184.26
|
194.68
|
261.96
|
275.94
|
|
1.2
|
52.23
|
78.73
|
100.45
|
151.78
|
182.43
|
|
1.3
|
19.26
|
37.66
|
56.16
|
89.61
|
122.16
|
|
1.4
|
8.90
|
20.24
|
33.98
|
56.15
|
85.37
|
|
1.5
|
4.93
|
11.99
|
21.96
|
37.24
|
62.27
|
|
1.6
|
3.14
|
7.71
|
14.99
|
25.93
|
47.12
|
|
1.7
|
2.24
|
5.31
|
10.72
|
18.80
|
36.76
|
|
1.8
|
1.75
|
3.88
|
7.97
|
14.10
|
29.42
|
|
1.9
|
1.46
|
2.99
|
6.13
|
10.89
|
24.05
|
|
2.0
|
1.29
|
2.40
|
4.86
|
8.63
|
20.01
|
|
2.5
|
1.02
|
1.28
|
2.14
|
3.58
|
9.67
|
|
3.0
|
1.00
|
1.05
|
1.39
|
2.06
|
5.74
|
|
3.5
|
1.00
|
1.01
|
1.13
|
1.47
|
3.85
|
Table 8 ARLs for the proposed chart for r0=370 when shape parameter is shifted when=3
From these tables, we noticed that the decreasing trend in ARLs as the shift constant
increases. We observed the same trend for other combination of parameters we considered.
Industrial application of proposed chart
The industrial application of the proposed control chart can be implemented as follows: Presume that the lifetime of an electronic equipment follows the log logistic distribution with shape parameter
=3. Assume that the target average life of electronic equipment is
= 1000 hours and r0= 370. Then from Equation (5) we have p0 = 0.5355. Also, from Table 4 we obtain the sample size of n = 23, a = 0.8671, L = 2.9981, LCL = 5 and UCL = 19. Thus the inspection time
=867 hours. Therefore, the proposed control chart works as follows:
Step 1. Take a sample of size 23 at each subgroup and put them on the life test during 867 hours. Plot the number of failed items (D) during the test.
Step 2. Declare the process as in–control if 5≤ D ≤ 19 otherwise process as out–of–control.
To demonstrate the performance of the proposed control chart methodology, the following steps depicts the generation of data using simulation from log logistic distribution and constructing the control chart:
Step 1: Choose a subgroup sample size n.
Step 2: Generate log logistic random variable X of size n with scale parameter
=1, shape parameters
.
Step 3: Obtain the chart statistic, the number of failures D for each subgroup.
Step 4: Repeat step 1 to step 3 until desired number of sample groups (m=20) are attained.
Step 5: Construct the control limits for the proposed chart.
Step 6: Plot all statistics D against their sample groups.
For this design, the first 20 samples of subgroup size 24 are generated from log logistic distribution with in–control parameters
=1,
and the second set of the 20 samples of subgroup size 24 are from log logistic distribution with parameters
=0.75,
(i.e. out–of–control situation having a shift of c=0.75). From Table 3, when ARL at 300 and in–control parameters we find control chart coefficient L is 2.9645, a is 0.5979 and n is 24. The life test termination time be t0=0.5979x0.46868=0.2802.
The values of D for in–control and shifted cases for each subgroup are reported as follows:
In–control: 2, 1, 1, 3, 2, 2, 1, 1, 2, 1, 2, 3, 1, 2, 3, 1, 2, 1, 3, 2.
Shifted : 2, 2, 3, 2, 4, 6, 1, 2, 3, 5, 5, 3, 3, 2, 1, 3, 7, 2, 3, 2.
The average of failure
is 1.6, using Eq. (7) the control limits for the proposed control chart is found as UCL=5.2227 and LCL=0. Figure 1 is the proposed control chart based on simulated data, along with chart statistics and control limits, can detect an out–of–control process after 26 samples, i.e. after the 6th sample of the shifted process as ARL1 is estimated to be 20.1 for a shift of 0.75. Thus the proposed chart efficiently detects the shift in the process.
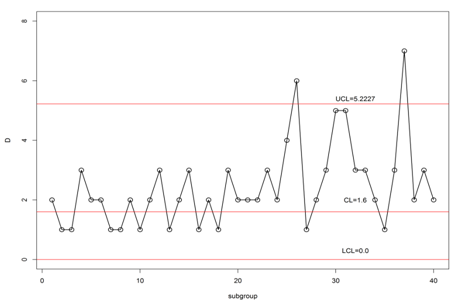
Figure 1 The proposed control chart for simulated data.


