eISSN: 2378-315X


Research Article Volume 8 Issue 6
1Department of Statistics, Ahmadu Bello University, Nigeria
2Department of Statistics, Federal University of Technology, Nigeria
Correspondence: Falgore Jamilu Yunusa, Department ofStatistics, Ahmadu Bello University, Zaria-Nigeria
Received: November 14, 2019 | Published: December 5, 2019
Citation: Falgore JY, Doguwa SI, Isah A. The Weibull-Inverse Lomax (WIL) distribution with Application on Bladder Cancer. Biom Biostat Int J. 2019;8(5):195-202. DOI: 10.15406/bbij.2019.08.00289
In this paper, we introduced a four-parameter probability model called Weibull-Inverse Lomax distribution with decreasing, increasing and bathtub hazard rate function. The WIL distribution density function is J-shaped, positively skewed, and J-shaped in reverse. Some of the mentioned distribution’s statistical characteristics are provided including moments, order statistics, entropy, mean, variance, moment generating function, and quantile function. The method of maximum likelihood estimation was used to estimate the parameters of the model. The distribution’s importance is proved by its implementation to the bladder cancer data set. Goodness-of-fit of this distribution by various techniques demonstrates that the WIL distribution is empirically better for lifetime application.
Keywords: entropy, moments, moment generating functions, Weibull-Inverse lomax distribution
Real life datasets can be fitted by utilizing a lot of existing statistical distributions. However, most of these real-world datasets does not follow these existing statistical distributions. Hence, the need to propose/develop new distributions that could describes some of these situations better and can also provide a better flexibility in the modelling of real-world data sets compared with the baseline distributions. As a result of this fact, researchers have developed many statistical families of distributions and study most of their properties. These include: The Transmuted Weibull lomax distribution by Afify et al.,1 kumaraswamy Marshal-olkin family by Afify et al.,2 Lomax generator by Cordeiro et al.,3 the weibull exponential by Oguntunde et al.,4 kumaraswamy-pareto by Bourguignon et al.,5 weibull-G family by Bourguignon et al.,6 the weibull-dagum distribution by Tahir et al.,7 the generalized transmuted-G family of distributions by Nofal et al.,8 among others. Recently, a lot of extensions of distributions have been proposed and studied based on the Weibull-G family of distributions by Bourguignon et al.,6 Among them is the Tahir, Merovci, Afify, Yousof, and Oguntunde et al.9-12,4 to mention but few.
Inverse Lomax distribution is a member of Beta-type distribution. Other members of the family include Dagum, lomax, Fisk or log-Logistics, Singh maddala, generalized beta distributions of the second kind among others, as in Kleiber et al.13 If a random variable say Z has a Lomax distribution, then has an Inverse Lomax distribution (ILD). It has been utilized to get the Lorenz ordering relationship among ordered statistics;.14 Apart from this, it has also many applications in economics, actuarial sciences, and stochastic modeling Kleiber C, Kotz S & Kleiber C13,14 have applied this model on geophysical data, specifically on the sizes of land fires in California state of US. Rahman et al.15 have discussed the estimation and prediction challenges for the inverse Lomax distribution via Bayesian approach. Yadav et al.16 have used this distribution for reliability estimation based on Type II censored observations. Some details about the Inverse Lomax distribution including its applications are available in Reyad and Othman, Falgore et al., Maxwell et al., and Hassan and Mohamed.17-23
The main aim of this paper is to provide an extension of the Inverse-Lomax distribution using the Weibull-G generator by Bourguignon et al.6 Therefore, we propose the Weibull-Inverse lomax (WIL) distribution by adding two extra shape parameters to the Inverse Lomax distribution.
The Inverse-Lomax distribution and Weibull G family
The probability density function (pdf) and cumulative distribution function (cdf) of ILD are given by the following equations as define by Yadav et al.16 as:
(1)
(2)
where x > 0, γ, λ > 0 are scale and shape parameters respectively.
denote the probability density function (pdf) and cumulative distribution function (cdf) of a baseline with parameter vector η and also consider the Weibull Cumulative Density Function (cdf) with positive parameters d and p. Based on this cdf, Bourguignon et al.6 replaced the argument x by , and defined the cdf and the pdf of the Weibull-G family by:
(3)
where G(x;η) is any baseline cdf which depends on a parameter vector η.
(4)
The interpretation of the family of distribution above as in Cooray21 is as follows. Let L be a lifetime random variable having a continuous cdf G(x;η), then the odds ratio that an individual (component) following the lifetime L will fail(die) at time x is . Let’s consider that the variability of this odds is represented by the random variable X and assume that it follows Weibull model with β as shape and α as scale, then
as given in equation 1 b.
A random variable X with density function in 1a is denoted by X∼Weib G(α,β,η). The extra parameters induced by the Weibull generator are sought just to increase the flexibity of the distribution. If β = 1, it corresponds to the Exponential-Generator by Gupta and Kundu.22
In this context, we proposed and study the WIL distribution based on equations 1a and 1 b.
The Weibull Inverse Lomax (WIL) Distribution
By inserting equation 1 in equation 1b yields the WIL cdf below:
(5)
The pdf corresponding to 5 is given by
where α > 0, β > 0 and λ are the shape parameters while γ is the scale parameter. Henceforth, we denote a random variable X having pdf 6 by X∼WIL(α, β, γ, λ).The hazard function h(x), cumulative hazard function H(x), survival function s(x),and reversed hazard rate r(x) of X are given by
(7)
(8)
(9)
(10)
Shapes of the Weibull-Inverse Lomax PDF, CDF, hazard and survival functions
The graphs below shows the shapes of the WIL density at various selected parameter values (Figure 1).
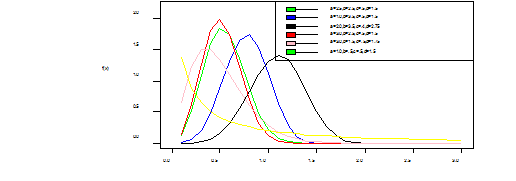
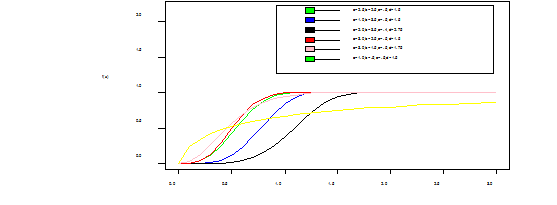


Figure 1 1a: Is the pdf of WIL which is unimodal and right skewed, 1b:Is the cdf of WIL which is J-shape which approaches each of the orthogonal axes asymptotically, 1c: Is the hazard function (bathtub curve) of WIL which is a decreasing failure rate function and lastly,1d: Is the survival function which shows that the probability that a subject will survive beyond time t, and its also a decreasing function.
Mixture representation
By inserting equations 2 and 1 in 1a we have
(11)
Let E be the last term of equation 11, by expanding E using power series
By inserting this expansion in equation 11 and after some algebra, we have
let
After simplifications and some algebra, we have
(12)
Where
Equation 12 reduces to
(13)
Where is the Inverse
Lomax density. By integrating Equation 13, the cdf of X can be given in the mixture form
(14)
Equation 13 above is the major result of this section.
Statistical Properties
Quantile function and median
Quantile function is used in drawing a sample from a particular distribution function. The quantile function of the WIL distribution is the inverse of 5 and is given by
(15)
where u∼ uniform(0,1) and random numbers can easily be generated from the WIL distribution using
The median of the WIL distribution can be derived by setting u = 0.5 in 16 to be
(16)
Moments
Must of the basic features and characteristics of a distribution can be studied through moments (for example kurtosis, tendency, skewness and dispersion). Theorem 4.1 If X∼WIL (α, β, γ, λ) then the rth moments of X is given as
(17)
Proof.
Let start the prove with the well known definition of the rth moment of the random variable X with probability density function f(x;α,β,γ,λ) given by
By substituting 13 in the above, we get
By letting and using the relation as in
(4) and some simplifications, we have equation 17.
The mean and the variance of the WIL distribution are:
(18)
Moment generating function
Theorem4.2 If X∼WIL (α,β,γ,λ) then the moment generating function (mgf) of X is given as
(20)
Proof
By definition, the mgf of a random variable X with density f(x) is given
By substituting in the above definition, we have
.
Order statistics
Order statistics are used in many areas of statistical theories and practices, for instance, detection of outlier in statistical quality control processes. In this section, we derive the closed form expressions for the pdf of the ith order statistic of the Weibull Inverse Lomax distribution. Suppose is a random sample from a distribution with pdf f(x) and Let denotes the corresponding order statistics obtained from this sample. Then
(21)
Where f(x) and F(x) are the pdf and cdf of Weibull Inverse Lomax distribution. Using the binomial expansion on
,
We have by substituting back in the above equation
(22)
By expanding the last term and further simplifications and algebra, we have
(23)
Where
and
denotes the Inverse lomax density function with parameters
Entropy
Rényi Entropy
The entropy of a random variable X is a measure of uncertain variation. we defined Rényi entropy by
By replacing f(x) with equation (13) we have
which can be reduced to
(24)
Where
q-entropy
The q-entropy, say is defined by ,
Where . From equation (24), we can obtain
(25)
Where
Estimation
Many parameter estimation techniques have been advocated in the literature, but the maximum likelihood method is the most frequently used. Furthermore, the MLEs have desirable properties and can be used to establish confidence intervals. The estimate of normality for these estimators is readily treated either numerically or analytically in the theory of large sample distribution. In this section, we determine the maximum likelihood estimates (MLEs) of the parameters of the Weibull Inverse Lomax distribution from complete samples only. Let be the observed values from the WIL distribution with parameter space be the parameter vector. The log-likelihood function for θ is given by
(26)
Differentiating with respect to each parameter and setting the result equals to zero, we obtain maximum likelihood estimates (MLEs). The partial derivatives of with respect to each parameter or the score function is given by:
where
(27)
(28)
(29)
(30)
In this section, we illustrate the applicability of the WIL distribution to the monthly remission of the 128 bladder cancer patients as reported by Maxwell et al.23 We estimated the parameters of each model by the method of Maximum Likelihood Estimation (MLE) using Simulated ANNealing (SANN) method. The goodness of fit statistics used in comparing the performances are Akaike Information Criterion AIC and Bayesian Information Criterion. Smaller values of the AIC and BIC statistics indicates better model fittings. Throughout the analysis, we used log-likelihood (- ll) value to derive the AIC and BIC by using the following relations: AIC = −2(−ll) + 2p and BIC = −2(−ll) + plog(n) where p is the number of parameters and n is the sample size. The data is given below:
0.08, 2.09, 3.48, 4.87, 6.94, 8.66, 13.11, 23.63, 0.20, 2.23, 3.52, 4.98, 6.97,
9.02, 13.29, 0.40, 2.26, 3.57, 5.06, 7.09, 9.22, 13.80, 25.74, 0.50, 2.46, 3.64,
5.09, 7.26, 9.47, 14.24, 25.82, 0.51, 2.54, 3.70, 5.17, 7.28, 9.74, 14.76, 26.31,
0.81, 2.62, 3.82, 5.32, 7.32, 10.06, 14.77, 32.15, 2.64, 3.88, 5.32, 7.39, 10.34,
14.83, 34.26, 0.90, 2.69, 4.18, 5.34, 7.59, 10.66, 15.96, 36.66, 1.05, 2.69, 4.23 , 5.41, 7.62, 10.75, 16.62, 43.01, 1.19, 2.75, 4.26, 5.41, 7.63, 17.12, 46.12, 1.26 ,
2.83, 4.33, 5.49, 7.66, 11.25, 17.14, 79.05, 1.35, 2.87, 5.62, 7.87, 11.64, 17.36,
1.40, 3.02, 4.34, 5.71, 7.93, 11.79, 18.10, 1.46, 4.40, 5.85, 8.26, 11.98, 19.13 , 1.76, 3.25, 4.50, 6.25, 8.37, 12.02, 2.02, 3.31, 4.51, 6.54, 8.53, 12.03, 20.28 ,
2.02, 3.36, 6.76, 12.07, 21.73, 2.07, 3.36, 6.93, 8.65, 12.63, 22.69. Firstly, it is usual to begin the analysis with plots of empirical distribution function and the histogram (density plot), as in figure 2a and Table 1. The left-hand plot is the histogram on a density scale and the right-hand plot is the empirical cumulative distribution function (CDF). While figure 2b is the skewness-kurtosis plot as proposed by Cullen & Aral et al.,24,25 in which the values for common distributions are displayed in order to guide the researcher for the choice of distributions to fit the data set. As in our case, Weibull distribution is suggested. For this data, we fit Weibull-Inverse Lomax (WIL) distribution defined in equation (6). Its fit is also compared with the Weibull-Lomax distribution by Tahir et al.,9 Weibull-Frechet by Atify et al.,11 Odd generalized exponential inverse lomax distribution by Falgore et al.,18 and Inverse lomax distribution as in Rahman et al.15 with the pdfs given below:
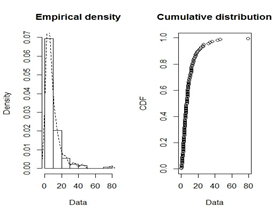
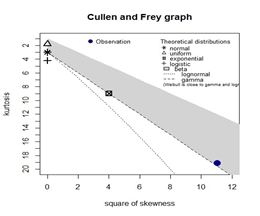
Figure 2 2a is the empirical and cdf plots of the data set and 2b is the Skewness-kurtosis plot for a bladder cancer patients data set.
Minimum |
Maximum |
Median |
Mean |
Est. Sd |
Est.Skewness |
Est.Kurtosis |
0.08 |
79.05 |
6.395 |
9.3656 |
10.5083 |
3.325 |
19.1537 |
Table 1 Summary Statistics of the Cancer patients’ data set
for
We have successfully proposed a flexible WIL distribution by extending the weibull-G family of Bourguignon et al.6 We have derived and studied some properties of this distribution including mean, variance, quantile, moments, moment generating function, entropies and order statistics. The parameters of the distribution were estimated by employing the method of maximum likelihood. Finally, an application of the WIL distribution to real data set is presented to show the importance and flexibility of the distribution. The AIC and BIC in Table 2 shows that the WIL distribution is the best model fitted.
Estimates |
- ll |
AIC |
BIC |
||||
Model |
α |
β |
γ |
λ |
|||
WIL(α,β,γ,λ) |
38.6899 |
0.0932 |
4.1773 |
15.7365 |
-353.4222 |
714.8443 |
726.252 |
WL(α,β,γ,λ) |
13.2986 |
1.3366 |
0.2175 |
10.4948 |
-410.4509 |
828.901 |
840.309 |
WFr(α,β,γ,λ) |
2.3452 |
0.3144 |
0.7016 |
26.8016 |
-621.6075 |
1251.215 |
1262.62 |
OGE-IL(α,β,γ,λ) |
0.8749 |
2.5967 |
1.4153 |
15.8219 |
-412.9428 |
833.8856 |
845.293 |
IL(γ,λ) |
- |
- |
2.0036 |
2.4603 |
-424.6757 |
853.3514 |
868.759 |
Table 1 Amplitude in mill volts of the Lead-1 of electrocardiography in sheep
*Significant (P≤0.05); NSNot significant (P>0.05)
No funding for this project and also no conflicts of interest among the authors.

©2019 Falgore, et al. This is an open access article distributed under the terms of the, which permits unrestricted use, distribution, and build upon your work non-commercially.
2 7