
Research Article Volume 3 Issue 5
On zero-truncation of poisson, poisson-lindley and poisson-sujatha distributions and their applications
Rama Shanker,1 
Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Hagos Fesshaye2
1Department of Statistics, Eritrea Institute of Technology, Eritrea
2Department of Economics, College of Business and Economics, Eritrea
Correspondence: Rama Shanker, Department of Statistics, Eritrea Institute of Technology, Asmara, Eritrea
Received: March 17, 2016 | Published: April 15, 2016
Citation: Shanker R, Fesshaye H. On zero-truncation of poisson, poisson-lindley and poisson-sujatha distributions and their applications. Biom Biostat Int J. 2016;3(4):125-135. DOI: 10.15406/bbij.2016.03.00072
Download PDF
Abstract
In the present paper, firstly the nature of zero-truncated Poisson distribution (ZTPD), zero-truncated Poisson-Lindley distribution (ZTPLD) and zero-truncated Poisson-Sujatha distribution (ZTPSD) have been discussed with graphs of their probability functions for different values of their parameter. Over-dispersion, equi-dispersion and under-dispersion of ZTPLD and ZTPSD have been discussed using index of dispersion. A simple and interesting method of finding moments of ZTPSD has been suggested and thus the first two moments about origin and the variance have been obtained. The estimation of parameter of ZTPD, ZTPLD and ZTPSD has been discussed using maximum likelihood estimation and method of moments.
The goodness of fit of ZTPD, ZTPLD, and ZTPSD using maximum likelihood estimate in zero-truncated data arising from demography, biological sciences and migration has been discussed and observed that in most data-sets relating to demography and biological sciences, ZTPSD gives better fit than ZTPD and ZTPLD.
Keywords: zero-truncated distribution, poisson-lindley distribution, poissonsujatha distribution, moments, estimation of parameter, goodness of fit
Introduction
Zero-truncated distributions, in probability theory, are certain discrete distributions having support the set of positive integers. These distributions are applicable for the situations when the data to be modeled originate from a mechanism that generates data excluding zero-counts.
Let
is the original distribution with support non negative positive integers. Then the zero-truncated version of
with the support the set of positive integers is given by
(1.1)
The Poisson-Lindley distribution (PLD) having probability mass function (p.m.f.)
(1.2)
has been introduced by Sankaran1 to model count data. Recently, Shanker & Hagos2 have done an extensive study on its applications to Biological Sciences and found that PLD provides a better fit than Poisson distribution to almost all biological science data. The PLD arises from the Poisson distribution when its parameter
follows Lindley3 with probability density function (p.d.f.)
(1.3)
Detailed study of Lindley distribution (1.3) has been done by Ghitany et al.4 and shown that (1.3) is a better model than exponential distribution for modeling some lifetime data. Recently, Shanker et al.5 showed that (1.3) is not always a better model than the exponential distribution for modeling lifetime’s data. In fact, Shanker et al.6 has done a very extensive and comparative study on modeling of lifetime data using exponential and Lindley distributions and discussed various lifetime data-sets to show the superiority of Lindley over exponential and that of exponential over Lindley distribution. The PLD has been extensively studied by Sankaran8 and Ghitany & Mutairi7 and its various properties have been discussed by them. The Lindley distribution and the PLD have been generalized by many researchers. Shanker & Mishra8 obtained a two parameter Poisson-Lindley distribution by compounding Poisson distribution with a two parameter Lindley distribution introduced by Shanker & Mishra.9 A quasi Poisson-Lindley distribution has been introduced by Shanker & Mishra10 by compounding Poisson distribution with a quasi Lindley distribution introduced by Shanker & Mishra.11 Shanker et al.12 obtained a discrete two parameter Poisson-Lindley distribution by mixing Poisson distribution with a two parameter Lindley distribution for modeling waiting and survival times data introduced by Shanker et al.13 Further, Shanker & Tekie14 obtained a new quasi Poisson-Lindley distribution by compounding Poisson distribution with a new quasi Lindley distribution introduced by Shanker & Amanuel.15
Recently Shanker16 has obtained Poisson-Sujatha distribution (PSD) having p.m.f.
(1.4)
to model count data in different fields of knowledge. The PSD arises from the Poisson distribution when its parameter
follows Shanker R17 with probability density function (p.d.f.)
(1.5)
Detailed discussion about its various properties, estimation of the parameter and applications for modeling lifetime data has been mentioned in Shanker17 and shown by Shanker17 that (1.5) is a better model than the exponential and Lindley3 distributions for modeling lifetime data. Shanker & Hagos18,19 has also obtained the size-biased and zero-truncated version of PSD and discussed their properties, estimation of parameter and applications in different fields of knowledge.
In this paper, the nature of zero-truncated Poisson distribution (ZTPD), zero-truncated Poisson-Lindley distribution (ZTPLD) and zero-truncated Poisson-Sujatha distribution has been compared and studied using graphs for different values of their parameter. A simple method for obtaining the moments of ZTPSD has been suggested and the first two moments about origin and variance have been obtained. ZTPD, ZTPLD and ZTPSD have been fitted to a number of data -sets from demography and biological sciences to study their goodness of fit and superiority of one over the others.
Zero-truncated poisson, poisson-lindley and poisson-sujatha distributions
Zero-truncated poisson distribution (ZTPD)
Using (1.1) and the p.m.f. of Poisson distribution, the p.m.f. of zero-truncated Poisson distribution (ZTPD) given by
(2.1.1)
was obtained independently by Plackett20 and David & Johnson21 to model count data excluding zero counts. An extension of a truncated Poisson distribution and estimation in a truncated Poisson distribution when zeros and some ones are missing has been discussed by Cohen.22,23 Tate & Goen24 have discussed minimum variance unbiased estimation (MVUE) for the truncated Poisson distribution.
Zero-truncated poisson-lindley distribution (ZTPLD)
Using (1.1) and (1.2), the p.m.f. of zero-truncated Poisson- Lindley distribution (ZTPLD) given by
(2.2.1)
was obtained by Ghitany et al.25 to model count data for the missing zeros.
Shanker et al.2 have done extensive study on the comparison of ZTPD and ZTPLD with respect to their applications in data - sets excluding zero-counts and showed that in demography and biological sciences ZTPLD gives better fit than ZTPD while in social sciences ZTPD gives better fit than ZTPLD.
Zero-truncated poisson-sujatha distribution (ZTPSD)
Using (1.1) and (1.4), the p.m.f. of zero-truncated Poisson-Sujatha distribution (ZTPSD) can be obtained as
(2.3.1)
The ZTPSD can also arise from the size-biased Poisson distribution (SBPD) with p.m.f.
(2.3.2)
When its parameter
follows a distribution having p.d.f.
(2.3.3)
The p.m.f. of ZTPSD is thus can be obtained as
(2.3.4)
which is the p.m.f. of ZTPSD with parameter
.
Shanker & Hagos19 have detailed study about its mathematical and statistical properties, estimation of parameter, and applications and showed that in many ways it has interesting advantage over ZTPLD and ZTPD.
To study the nature and behaviors of ZTPD, ZTPLD and ZTPSD for different values of their parameter, a number of graphs of their probability functions have been drawn and presented in Figure 1.
Moments and related measures of ZTPSD
The
th moment about origin of ZTPSD (2.3.1) can be obtained as
(3.1)
Clearly the expression under the bracket in (3.1) is the
th moment about origin of the SBPD. Taking
in (3.1) and using the first moment about origin of the SBPD, the first moment about origin of the ZTPSD (2.3.1) can be obtained as
(3.2)
Again taking
in (3.1) and using the second moment about origin of the SBPD, the second moment about origin of the ZTPSD (2.3) can be obtained as
(3.3.3)
Similarly, taking
in (3.1) and using the respective moments of SBPD, the third and the fourth moment about origin of ZTPSD can be obtained. The variance of ZTPSD (2.3. 1) are thus obtained as
The index of dispersion of ZTPSD (2.3.1) is given by
It can be easily verified that the ZTPSD is over dispersed
, equi-dispersed
and under dispersed
for
1.548328 respectively. It is to noted that ZTPLD is over dispersed
, equi-dispersed
and under dispersed
for
1.258627 respectively.
Estimation of the parameter
Estimation of parameter of ZTPD
Let
be a random sample of size
from the ZTPD (2.1.1). The maximum likelihood estimate (MLE) and method of moment estimate (MOME) of
of ZTPD (2.1.1) is given by the solution of the following non linear equation
, where
is the sample mean.
Estimation of parameter of ZTPLD
Maximum likelihood estimate (MLE):
The maximum likelihood estimate
of
of ZTPLD is the solution of the following non-linear equation
Where
is the sample mean. This non-linear equation can be solved by any numerical iteration methods such as Newton-Raphson method, Bisection method, Regula-Falsi method etc. Ghitany et al.25 showed that the MLE
of
is consistent and asymptotically normal.
Method of moment estimate (MOME): Equating the population mean to the corresponding sample mean, the MOME
of
of ZTPLD (2.2.1) is the solution of the following cubic equation
, where
is the sample mean. Ghitany et al.25 showed that the MOME
of
is consistent and asymptotically normal.
Estimation of parameter of ZTPSD
Maximum likelihood estimate (MLE): The maximum likelihood estimate
of
of ZTPSD is the solution of the following non-linear equation
Where
is the sample mean. This non-linear equation can be solved by any numerical iteration methods such as Newton-Raphson, Bisection method, Regula-Falsi method etc.
Method of moment estimate (MOME): Equating the population mean to the corresponding sample mean, the method of moment estimate (MOME)
of
of ZTPSD is the solution of the following non-linear equation
Where
is the sample mean?
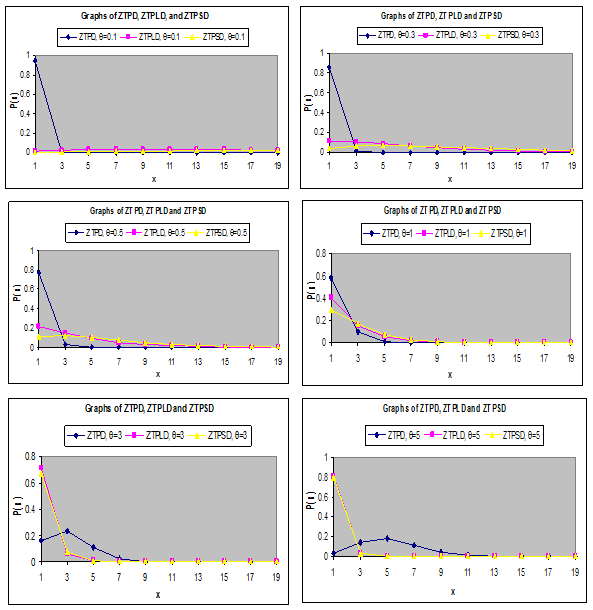
Figure 1 Graph of probability mass functions of ZTPD, ZTPLD and ZTPSD for different values of their parameter.
Applications and goodness of fit
In this section, an attempt has been made to test the suitability of ZTPD, ZTPLD and ZTPSD in describing the neonatal deaths as well as of infant and child deaths experienced by mothers. The data-sets considered here are the data of Sri Lanka and India. The data-sets of Meegama26 have been used as the data of Sri Lanka whereas the data from the survey conducted by Lal27 and the survey of Kadam Kuan, Patna, conducted in 1975 and referred to by Mishra28 have been used as the data of India. Further, ZTPD, ZTPLD, and ZTPSD have also been fitted to data on migration. It is obvious from the fitting of ZTPD, ZTPLD and ZTPSD that ZTPSD and ZTPLD are competitive distributions for modeling data from demography (Table A1-A8).
Number of neonatal deaths |
Observed number of mothers |
Expected frequency |
ZTPD |
ZTPLD |
ZTPSD |
1 |
409 |
399.7 |
408.1 |
408.2 |
2 |
88 |
102.3 |
89.4 |
89.2 |
3 |
19 |
|
19.3
|
19.3
|
4 |
5 |
5 |
1 |
Total |
522 |
522.0 |
522.0 |
522.0 |
ML Estimate |
|
|
|
|
|
|
3.464 |
0.145 |
0.113 |
d.f. |
|
1 |
2 |
2 |
P-value |
|
0.0627 |
0.9301 |
0.945 |
Table A1 The number of mothers of the rural area having at least one live birth and one neonatal death
Number of Neonatal Deaths |
Observed number of mothers |
Expected frequency |
ZTPD |
ZTPLD |
ZTPSD |
1 |
71 |
66.5 |
72.3 |
72.1 |
2 |
32 |
35.1 |
28.4 |
28.6 |
3 |
7 |
|
10.9
|
10.9
|
4 |
5 |
5 |
3 |
Total |
118 |
118.0 |
118.0 |
118.0 |
ML Estimate |
|
|
|
|
|
|
0.696 |
2.274 |
2.215 |
d.f. |
|
1 |
2 |
2 |
P-value |
|
0.4041 |
0.3208 |
0.3303 |
Table A2 The number of mothers of the estate area having at least one live birth and one neonatal death
Number of infant and child deaths |
Observed number of mothers |
Expected frequency |
ZTPD |
ZTPLD |
ZTPSD |
1 |
176 |
164.3 |
171.6 |
171.6 |
2 |
44 |
61.2 |
51.3 |
51.3 |
3 |
16 |
|
15
|
15.1
|
4 |
6 |
5 |
2 |
Total |
244 |
244.0 |
244.0 |
244.0 |
ML Estimate |
|
|
|
|
|
|
7.301 |
1.882 |
1.869 |
d.f. |
|
1 |
2 |
2 |
P-value |
|
0.0069 |
0.3902 |
0.3927 |
Table A3 The number of mothers of the urban area with at least two live births by the number of infant and child deaths
Number of infant and child deaths |
Observed number of mothers |
Expected frequency |
ZTPD |
ZTPLD |
ZTPSD |
1 |
745 |
708.9 |
738.1 |
738.1 |
2 |
212 |
255.1 |
214.8 |
214.9 |
3 |
50 |
61.2 |
61.3 |
61.3 |
4 |
21 |
|
17.2
|
17.2
|
5 |
7 |
6 |
3 |
Total |
1038 |
1038.0 |
1038.0 |
1038.0 |
ML Estimate |
|
|
|
|
|
|
37.046 |
4.773 |
4.909 |
d.f. |
|
2 |
3 |
3 |
P-value |
|
0 |
0.1892 |
0.1785 |
Table A4 The number of mothers of the rural area with at least two live births by the number of infant and child deaths
Number of Infant Deaths |
Observed number of Mothers |
Expected Frequency |
ZTPD |
ZTPLD |
ZTPSD |
1 |
683 |
659.0 |
674.4 |
674.7 |
2 |
145 |
177.4 |
154.1 |
153.8 |
3 |
29 |
|
34.6
|
34.7
|
4 |
11 |
5 |
5 |
Total |
873 |
873.0 |
873.0 |
873.0 |
ML Estimate |
|
|
|
|
|
|
8.718 |
5.310 |
5.463 |
d.f. |
|
1 |
2 |
2 |
P-value |
|
0.0031 |
0.0703 |
0.0651 |
Table A5 The number of literate mothers with at least one live birth by the number of infant deaths
Number of child deaths |
Observed number of mothers |
Expected frequency |
ZTPD |
ZTPLD |
ZTPSD |
1 |
89 |
76.8 |
83.4 |
83.3 |
2 |
25 |
39.9 |
32.3 |
32.5 |
3 |
11 |
|
12.2
|
12.2
|
4 |
6 |
5 |
3 |
6 |
1 |
Total |
135 |
135.0 |
135.0 |
135.0 |
ML Estimate |
|
|
|
|
|
|
7.90 |
3.428 |
3.523 |
d.f. |
|
1 |
2 |
2 |
P-value |
|
0.0049 |
0.1801 |
0.1717 |
Table A6 The number of mothers of the completed fertility having experienced at least one child death
Number of neonatal deaths |
Observed number of mothers |
Expected frequency |
ZTPD |
ZTPLD |
ZTPSD |
1 |
567 |
545.8 |
561.4 |
561.5 |
2 |
135 |
162.5 |
139.7 |
139.5 |
3 |
28 |
32.3 |
34.2 |
34.2 |
4 |
11 |
|
|
|
5 |
5 |
Total |
746 |
746.0 |
746.0 |
746.0 |
ML Estimate |
|
|
|
|
|
|
26.855 |
3.839 |
3.824 |
d.f. |
|
2 |
2 |
2 |
P-value |
|
0.0 |
0.1467 |
0.1477 |
Table A7 The number of mothers having at least one neonatal death
Number of migrants |
Observed frequency |
Expected frequency |
ZTPD |
ZTPLD |
ZTPSD |
1 |
375 |
354.0 |
379.0 |
378.3 |
2 |
143 |
167.7 |
137.2 |
137.8 |
3 |
49 |
53.0 |
48.4 |
48.7 |
4 |
17 |
|
16.8
|
16.8
|
5 |
2 |
6 |
2 |
7 |
1 |
8 |
1 |
Total |
590 |
590.0 |
590.0 |
590.0 |
ML Estimate |
|
|
|
|
|
|
8.933 |
1.031 |
0.912 |
d.f. |
|
2 |
3 |
3 |
P-value |
|
0.0115 |
0.7937 |
0.8225 |
Table A8 Number of households having at least one migrant according to the number of migrants, reported by Singh & Yadav29
Biological sciences
In this section, an attempt has been made to test the goodness of fit of ZTPD, ZTPLD and ZTPSD on many data- sets relating to biological sciences and it is obvious from the fitting of these distributions that ZTPSD gives much closer fit than ZTPD and ZTPLD in almost all cases. Thus in biological sciences ZTPSD is a better model than ZTPD and ZTPSD to model zero-truncated count data (Table B1-B6).
Number of european red mites |
Observed frequency |
Expected frequency |
ZTPD |
ZTPLD |
ZTPSD |
1 |
38 |
28.7 |
36.1 |
35.5 |
2 |
17 |
25.7 |
20.5 |
20.8 |
3 |
10 |
15.3 |
11.2 |
11.5 |
4 |
9 |
|
5.9
|
6.1
|
5 |
3 |
6 |
2 |
7 |
1 |
8 |
0 |
Total |
80 |
80.0 |
80.0 |
80.0 |
ML Estimate |
|
|
|
|
|
|
9.827 |
2.467 |
2.444 |
d.f. |
|
2 |
3 |
3 |
P-value |
|
0.0073 |
0.4813 |
0.4854 |
Table B1 Number of European red mites on apple leaves, reported by Garman30
Number of yeast cells counts per mm square |
Observed frequency |
Expected frequency |
ZTPD |
ZTPLD |
ZTPSD |
1 |
128 |
121.3 |
127.6 |
127.4 |
2 |
37 |
49.2 |
40.9 |
41 |
3 |
18 |
|
|
|
4 |
3 |
5 |
1 |
6 |
0 |
Total |
187 |
187.0 |
187.0 |
187.0 |
ML Estimate |
|
|
|
|
|
|
5.228 |
1.034 |
1.013 |
d.f. |
|
1 |
1 |
1 |
P-value |
|
0.0222 |
0.3092 |
0.3141 |
Table B2 Number of yeast cell counts observed per mm square, reported by Student31
Number of leaf spot grade |
Observed frequency |
Expected frequency |
ZTPD |
ZTPLD |
ZTPSD |
1 |
18 |
14.2 |
23.0 |
21.7 |
2 |
15 |
18.7 |
16.3 |
16.5 |
3 |
10 |
16.5 |
11.1 |
11.6 |
4 |
14 |
10.9 |
7.3 |
7.8 |
5 |
13 |
9.7 |
12.3 |
12.4 |
Total |
70 |
70.0 |
70.0 |
70.0 |
ML Estimate |
|
|
|
|
|
|
6.311 |
7.476 |
5.943 |
d.f. |
|
3 |
3 |
3 |
P-value |
|
0.0974 |
0.0582 |
0.1144 |
Table B3 The number of leaf spot grade of Ichinose variety of Mulberry, reported by Khurshid32
Number of leaf spot grade |
Observed frequency |
Expected frequency |
ZTPD |
ZTPLD |
ZTPSD |
1 |
37 |
28.5 |
36.7 |
35.9 |
2 |
16 |
26.7 |
21.4 |
21.8 |
3 |
15 |
16.7 |
12.0 |
12.4 |
4 |
8 |
|
6.6 |
6.8 |
5 |
8 |
7.3 |
7.1 |
Total |
84 |
84.0 |
84.0 |
84.0 |
ML Estimate |
|
|
|
|
|
|
8.329 |
2.477 |
2.446 |
d.f. |
|
2 |
3 |
3 |
P-value |
|
0.0155 |
0.4795 |
0.4851 |
Table B4 The number of leaf spot grade of Kokuso-20 variety of Mulberry, reported by Khurshid32
Number of sites with particles |
Observed frequency |
Expected frequency |
ZTPD |
ZTPLD |
ZTPSD |
1 |
122 |
115.9 |
124.8 |
124.4 |
2 |
50 |
57.4 |
46.8 |
47.0 |
3 |
18 |
18.9 |
17.1 |
17.2 |
4 |
4 |
|
|
|
5 |
4 |
Total |
198 |
198.0 |
198.0 |
198.0 |
ML Estimate |
|
|
|
|
|
|
2.140 |
0.510 |
0.460 |
d.f. |
|
2 |
2 |
2 |
P-value |
|
0.3430 |
0.7749 |
0.7945 |
Table B5 The number of counts of sites with particles from Immunogold data reported by Mathews & Appleton33
Number of times hares caught |
Observed frequency |
Expected frequency |
ZTPD |
ZTPLD |
ZTPSD |
1 |
184 |
176.6 |
182.6 |
182.6 |
2 |
55 |
66.0 |
55.3 |
55.3 |
3 |
14 |
|
16.4
|
16.4
|
4 |
4 |
5 |
4 |
Total |
261 |
261.0 |
261.0 |
261.0 |
ML Estimate |
|
|
|
|
|
|
2.450 |
0.610 |
0.575 |
d.f. |
|
1 |
2 |
2 |
P-value |
|
0.1175 |
0.7371 |
0.7501 |
Table B6 The number of snowshoe hares counts captured over 7 days, reported by Keith & Meslow34,35
Concluding remarks
In this paper, the nature and behavior of ZTPD, ZTPLD and ZTPSD have been studied by drawing different graphs of their probability functions for the different values of their parameter. A very simple and easy method for finding moments of ZTPSD has been suggested. An attempt has been made to study the goodness of fit of ZTPD, ZTPLD and ZTPSD to count data relating to demography and biological sciences and it has been observed that ZTPSD is a better model than the ZTPD and ZTPLD in almost all data-sets relating to mortality, migration and biological sciences.
Acknowledgments
Conflicts of interest
Author declares that there are no conflicts of interest.
References
- Sankaran M. The discrete Poisson-Lindley distribution. Biometrics. 1970;26:145–149.
- Shanker R, Hagos F. On Poisson-Lindley distribution and Its Applications to Biological Sciences. Biometrics and Biostatistics International Journal. 2015;2(4):1–5.
- Lindley DV. Fiducial distributions and Bayes’ Theorem. Journal of the Royal Statistical Society. 1958;20(1):102–107.
- Ghitany ME, Atieh B, Nadarajah S. Lindley distribution and Its Applications. Mathematics Computation and Simulation. 2008a;78(4):493–506.
- Shanker R, Hagos F, Sujatha S. On modeling of Lifetimes data using exponential and Lindley distributions. Biometrics and Biostatistics International Journal. 2015;2(5):1–9.
- Shanker R, Hagos F, Sujatha S, et al. On Zero-truncation of Poisson and Poisson-Lindley distributins and Their Applications. Biometrics and Biostatistics International Journal. 2015;2(6):1–14
- Ghitany ME, Al Mutairi DK. Estimation Methods for the discrete Poisson-Lindley distribution. Journal of Statistical Computation and Simulation. 2009;79(1):1–9.
- Mishra A. A two-parameter Poisson-Lindley distribution. International Journal of Statistics and Systems. 2014;9(1):79–85.
- Shanker R, Mishra A. A two-parameter Lindley distribution. Statistics in Transition new Series. 2013a;14(1):45–56.
- Shanker R, Mishra A. A quasi Poisson-Lindley distribution. Accepted in Journal of Indian Statistical Association. 2015.
- Shanker R, Mishra A. A quasi Lindley distribution. African journal of Mathematics and Computer Science Research. 2013b;6(4):64–71.
- Shanker R, Sharma S, Shanker R. A Discrete two-Parameter Poisson Lindley Distribution. Journal of Ethiopian Statistical Association. 2012;21:15–22.
- Shanker R, Sharma S, Shanker R. A two-parameter Lindley distribution for modeling waiting and survival times data. Applied Mathematics. 2013;4(2):363–368.
- Shanker R, Tekie AL. A new quasi Poisson-Lindley distribution. International Journal of Statistics and Systems. 2013;9(1):87–94.
- Shanker R, Amanuel AG. A new quasi Lindley distribution. International Journal of Statistics and Systems. 2013;6(4):143–156.
- Shanker R. The discrete Poisson-Sujatha distribution. International Journal of Probability and Statistics. 2016b;5(1):1–9.
- Shanker R. Sujatha distribution and Its Applications. Accepted for publication in “Statistics in Transition-new Series”. 2016a.
- Shanker R, Hagos F. Size-Biased Poisson-Sujatha distribution with Applications, Communicated. 2016a.
- Shanker R, Hagos F. Zero-truncated Poisson-Sujatha distribution with Applications. Communicated. 2016b.
- Plackett RL. The truncated Poisson-distribution. Biometrics. 1953;9(4):485–488.
- David FN, Johnson NL. The truncated Poisson. Biometrics. 1952;8:275–285.
- Cohen AC. An extension of a truncated Poisson distribution. Biometrics. 1960a;16(3):446–450.
- Cohen AC. Estimation in a truncated Poisson distribution when zeros and some ones are missing. Journal of American Statistical Association. 1960b;55:342–348.
- Tate RF, Goen RL. MVUE for the truncated Poisson distribution. Annals of Mathematical Statistics. 1959;29:755–765.
- Ghitany ME, Al Mutairi DK, Nadarajah S. Zero-truncated Poisson-Lindley distribution and its Applications. Mathematics and Computers in Simulation. 2008b;79(3):279–287.
- Meegama SA. Socio-economic determinants of infant and child mortality in Sri Lanka, an analysis of postwar experience. International Statistical Institute. 1980;55.
- Lal DN. Patna in 1955: A Demographic Sample Survey, Demographic Research Center, Department of Statistics, Patna University, Patna, India. 1955.
- Mishra A. Generalizations of some discrete distributions. Patna University, Patna, India. 1979.
- Singh SN, Yadav RC. Trends in rural out-migration at household level. Rural Demography. 1971;8:53–61.
- Garman P. The European red mites in Connecticut apple orchards, Connecticut. Agri Exper Station Bull. 1953;252:103–125.
- Student. On the error of counting with a haemacytometer. Biometrika. 1907;5(3):351–360.
- Khursid AM. On size-biased Poisson distribution and Its use in zero-truncated case. Journal of the Korean Society for Industrial and Applied Mathematics. 2008;12(3):153–160.
- Mathews JNS, Appleton DR. An application of the truncated Poisson distribution to Immunogold assay. Biometrics. 1953;49(2):617–621.
- Keith LB, Meslow EC. Trap response by snowshoe hares. The Journal of Wildlife Management. 1968;32(4):795–801.
- Finney DJ, Varley GC. An example of the truncated Poisson distribution. Biometrics. 1955;11(3):387–394.

©2016 Shanker, et al. This is an open access article distributed under the terms of the,
which
permits unrestricted use, distribution, and build upon your work non-commercially.


