Zero-truncated poisson distribution (ZTPD)

Using (1.1) and the p.m.f. of Poisson distribution, the p.m.f. of zero-truncated Poisson distribution (ZTPD) given by
$P_1\left(x;\theta \right)=\frac{{\theta }^x}{\left(e^{\theta }-1\right)x!};x=1,2,3,\mathrm{....},\theta >0$ (2.1.1)
was obtained independently by Plackett¹ and David et al.¹⁶ to model count data that structurally excludes zero counts. An extension of a truncated Poisson distribution and estimation in a truncated Poisson distribution when zeros and some ones are missing has been discussed by Cohen.^17,18 Tate et al.¹⁹ has discussed minimum variance unbiased estimation (MVUE) for the truncated Poisson distribution.

Zero-truncated poisson-Lindley distribution (ZTPLD)

Using (1.1) and (1.2), the p.m.f. of zero-truncated Poisson- Lindley distribution (ZTPLD) given by
$P_2\left(x;\theta \right)=\frac{{\theta }^2}{{\theta }^2+3\theta +1}\frac{x+\theta +2}{{\left(\theta +1\right)}^x};x=1,2,3,\mathrm{....},\theta >0$ (2.2.1)
was obtained by Ghitany et al.²⁰ to model count data for the missing zeros. It has been shown by Ghitany et al.²⁰ that ZTPLD can also arise from the size-biased Poisson distribution (SBPD) with p.m.f.
$f\left(x|\lambda \right)=\frac{e^{-\lambda }{\lambda }^{x-1}}{\left(x-1\right)!};x=1,2,3,\mathrm{...},\lambda >0$ (2.2.2)
when its parameter $\lambda$ follows a distribution having p.d.f.
$h\left(\lambda ;\theta \right)=\frac{{\theta }^2}{{\theta }^2+3\theta +1}\left[\left(\theta +1\right)\lambda +\left(\theta +2\right)\right]e^{-\theta \lambda };\lambda >0,\theta >0$  (2.2.3)
Thus the p.m.f. of ZTPLD is obtained as
$P\left(X=x\right)={\displaystyle \underset{0}{\overset{\infty }{\int }}f\left(x|\lambda \right)}\cdot h\left(\lambda ;\theta \right)d\lambda$
$={\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{e^{-\lambda }{\lambda }^{x-1}}{\left(x-1\right)!}}\cdot \frac{{\theta }^2}{{\theta }^2+3\theta +1}\left[\left(\theta +1\right)\lambda +\left(\theta +2\right)\right]e^{-\theta \lambda }d\lambda$  (2.2.4)
$=\frac{{\theta }^2}{\left({\theta }^2+3\theta +1\right)\left(x-1\right)!}{\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-\left(\theta +1\right)\lambda }}\cdot \left[\left(\theta +1\right){\lambda }^x+\left(\theta +2\right){\lambda }^{x-1}\right]d\lambda$
$=\frac{{\theta }^2}{{\theta }^2+3\theta +1}\left[\frac{x}{{\left(\theta +1\right)}^x}+\frac{\left(\theta +2\right)}{{\left(\theta +1\right)}^x}\right]$
$=\frac{{\theta }^2}{{\theta }^2+3\theta +1}\frac{x+\theta +2}{{\left(\theta +1\right)}^x};x=1,2,3,\mathrm{...},\theta >0$
which is the p.m.f. of ZTPLD with parameter$\theta$ .
To study the nature and behaviors of ZTPD and ZTPLD for different values of its parameter, a number of graphs of their probability densities have been drawn and presented in Figure 1.

Moments of ZTPD

 The $r$ th factorial moment of the ZTPD (2.1.1) can be obtained as
${\mu }_{\left(r\right)}{}^{\prime }=E\left[X^{\left(r\right)}\right]=\frac{1}{e^{\theta }-1}{\displaystyle \sum _{x=1}^{\infty }{x}^{\left(r\right)}}\frac{{\theta }^x}{x!}$ , where $X^{\left(r\right)}=X(X-1)(X-2)\mathrm{...}(X-r+1)$
$=\frac{{\theta }^r}{e^{\theta }-1}{\displaystyle \sum _{x=r}^{\infty }\frac{{\theta }^{x-r}}{\left(x-r\right)!}=\frac{{\theta }^r{e}^{\theta }}{e^{\theta }-1}}$ (3.1.1)
Substituting $r=1,2,3,\text{and}\text{4}$ in (3.1.1), the first four factorial moments can be obtained and, therefore, using the relationship between factorial moments and moments about origin, the first four moments about origin of ZTPD (2.1.1) are obtained as
${\mu }_1{}^{\prime }=\frac{\theta e^{\theta }}{e^{\theta }-1}$
${\mu }_2{}^{\prime }=\frac{\theta e^{\theta }}{e^{\theta }-1}\left(\theta +1\right)$
${\mu }_3{}^{\prime }=\frac{\theta e^{\theta }}{e^{\theta }-1}\left({\theta }^2+3\theta +1\right)$
${\mu }_3{}^{\prime }=\frac{\theta e^{\theta }}{e^{\theta }-1}\left({\theta }^3+6{\theta }^2+7\theta +1\right)$

Generating Function: The probability generating function of the ZTPD (2.1.1) is obtained as
$P_X\left(t\right)=E\left(t^X\right)=\frac{1}{e^{\theta }-1}{\displaystyle \sum _{x=1}^{\infty }\frac{{\left(\theta t\right)}^x}{x!}}=\frac{1}{e^{\theta }-1}\left[{\displaystyle \sum _{x=0}^{\infty }\frac{{\left(\theta t\right)}^x}{x!}-1}\right]=\frac{e^{\theta t}-1}{e^{\theta }-1}$
The moment generating function of the ZTPD (2.1.1) is thus given by
$M_X\left(t\right)=E\left(e^{tX}\right)=\frac{e^{\theta e^t}-1}{e^{\theta }-1}$

Moments of ZTPLD

The $r$ th factorial moment of the ZTPLD (2.2.1) can be obtained as
${\mu }_{\left(r\right)}{}^{\prime }=E\left[X^{\left(r\right)}|\lambda \right]$ , where $X^{\left(r\right)}=X(X-1)(X-2)\mathrm{...}(X-r+1)$
Using (2.2.4), we get
${\mu }_{\left(r\right)}{}^{\prime }={\displaystyle \underset{0}{\overset{\infty }{\int }}\left[{\displaystyle \sum _{x=1}^{\infty }{x}^{\left(r\right)}\frac{e^{-\lambda }{\lambda }^{x-1}}{\left(x-1\right)!}}\right]}\cdot \frac{{\theta }^2}{{\theta }^2+3\theta +1}\left[\left(\theta +1\right)\lambda +\left(\theta +2\right)\right]e^{-\theta \lambda }d\lambda$
$={\displaystyle \underset{0}{\overset{\infty }{\int }}\left[{\lambda }^{r-1}{\displaystyle \sum _{x=r}^{\infty }x\frac{e^{-\lambda }{\lambda }^{x-r}}{\left(x-r\right)!}}\right]}\cdot \frac{{\theta }^2}{{\theta }^2+3\theta +1}\left[\left(\theta +1\right)\lambda +\left(\theta +2\right)\right]e^{-\theta \lambda }d\lambda$
Taking $x+r$ in place of $x$ , we get
${\mu }_{\left(r\right)}{}^{\prime }={\displaystyle \underset{0}{\overset{\infty }{\int }}{\lambda }^{r-1}\left[{\displaystyle \sum _{x=0}^{\infty }\left(x+r\right)\frac{e^{-\lambda }{\lambda }^x}{x!}}\right]}\cdot \frac{{\theta }^2}{{\theta }^2+3\theta +1}\left[\left(\theta +1\right)\lambda +\left(\theta +2\right)\right]e^{-\theta \lambda }d\lambda$
It is obvious that the expression within the bracket is $\lambda +r$ and hence, we have
${\mu }_{\left(r\right)}{}^{\prime }=\frac{{\theta }^2}{{\theta }^2+3\theta +1}{\displaystyle \underset{0}{\overset{\infty }{\int }}{\lambda }^{r-1}\left(\lambda +r\right)}\cdot \left[\left(\theta +1\right)\lambda +\left(\theta +2\right)\right]e^{-\theta \lambda }d\lambda$
Using gamma integral and little algebraic simplification, we get finally, a general expression for the $r$ th factorial moment of the ZTPLD (2.2.1) as
${\mu }_{\left(r\right)}{}^{\prime }=\frac{r!{\left(\theta +1\right)}^2\left(r+\theta +1\right)}{{\theta }^r\left({\theta }^2+3\theta +1\right)};r=1,2,3,\mathrm{...}$ (3.2.1)
Substituting $r=1,2,3,\text{and}4$ in (3.2.1), the first four factorial moment can be obtained and then using the relationship between factorial moments and moments about origin, the first four moments about origin of the ZTPLD (2.2.1) are given by
${\mu }_1{}^{\prime }=\frac{{\left(\theta +1\right)}^2\left(\theta +2\right)}{\theta \left({\theta }^2+3\theta +1\right)}$
${\mu }_2{}^{\prime }=\frac{{\left(\theta +1\right)}^2\left({\theta }^2+4\theta +6\right)}{{\theta }^2\left({\theta }^2+3\theta +1\right)}$
${\mu }_3{}^{\prime }=\frac{{\left(\theta +1\right)}^2\left({\theta }^3+8{\theta }^2+24\theta +24\right)}{{\theta }^3\left({\theta }^2+3\theta +1\right)}$
${\mu }_4{}^{\prime }=\frac{{\left(\theta +1\right)}^2\left({\theta }^4+16{\theta }^3+78{\theta }^2+168\theta +120\right)}{{\theta }^4\left({\theta }^2+3\theta +1\right)}$

Generating function: The probability generating function of the ZTPLD (2.2.1) is obtained as
$P_X\left(t\right)=E\left(t^X\right)=\frac{{\theta }^2}{{\theta }^2+3\theta +1}{\displaystyle \sum _{x=1}^{\infty }{t}^x}\frac{x+\theta +2}{{\left(\theta +1\right)}^x}$
$=\frac{{\theta }^2}{{\theta }^2+3\theta +1}\left[{\displaystyle \sum _{x=1}^{\infty }x{\left(\frac{t}{\theta +1}\right)}^x+\left(\theta +2\right){\displaystyle \sum _{x=1}^{\infty }{\left(\frac{t}{\theta +1}\right)}^x}}\right]$
$=\frac{{\theta }^{2}t}{{\theta }^2+3\theta +1}\left[\frac{\theta +1}{{\left(\theta +1-t\right)}^2}+\frac{\theta +2}{\theta +1-t}\right]$
The moment generating function of the ZTPLD (2.2.1) is thus given by
$M_X\left(t\right)=E\left(e^{tX}\right)=\frac{{\theta }^2{e}^t}{{\theta }^2+3\theta +1}\left[\frac{\theta +1}{{\left(\theta +1-e^t\right)}^2}+\frac{\theta +2}{\theta +1-e^t}\right]$

Using (2.2.4), the $r$ th moment about origin of ZTPLD (2.2.1) can be obtained as
${{\mu }^{\prime }}_r=E\left[E\left(X^r|\lambda \right)\right]$  
$=\frac{{\theta }^2}{{\theta }^2+3\theta +1}{\displaystyle \underset{0}{\overset{\infty }{\int }}\left[{\displaystyle \sum _{x=1}^{\infty }{x}^r}\frac{e^{-\lambda }{\lambda }^{x-1}}{\left(x-1\right)!}\right]}\cdot \left[\left(\theta +1\right)\lambda +\left(\theta +2\right)\right]e^{-\theta \lambda }d\lambda$  (4.1)
It is obvious that the expression under the bracket in (4.1) is the $r$ th moment about origin of the SBPD. Taking $r=1$  in (4.1) and using the first moment about origin of the SBPD, the first moment about origin of the ZTPLD (2.2.1) is obtained as
${{\mu }^{\prime }}_1=\frac{{\theta }^2}{{\theta }^2+3\theta +1}{\displaystyle \underset{0}{\overset{\infty }{\int }}\left(\lambda +1\right)}\left[\left(\theta +1\right)\lambda +\left(\theta +2\right)\right]e^{-\theta \lambda }d\lambda$  $=\frac{{\left(\theta +1\right)}^2\left(\theta +2\right)}{\theta \left({\theta }^2+3\theta +1\right)}$  (4.2)
Again taking $r=2$  in (4.1) and using the second moment about origin of the SBPD, the second moment about origin of the ZTPLD (2.2.1) is obtained as
${{\mu }^{\prime }}_2=\frac{{\theta }^2}{{\theta }^2+3\theta +1}{\displaystyle \underset{0}{\overset{\infty }{\int }}\left({\lambda }^2+3\lambda +1\right)}\left[\left(\theta +1\right)\lambda +\left(\theta +2\right)\right]e^{-\theta \lambda }d\lambda$
$=\frac{{\left(\theta +1\right)}^2\left({\theta }^2+4\theta +6\right)}{{\theta }^2\left({\theta }^2+3\theta +1\right)}$ (4.3)
Similarly, taking $r=3\text{and}4$ in (4.1) and using the respective moments of SBPD, we get finally, after a little simplification, the third and the fourth moments about origin of the ZTPLD (2.2.1) as
${{\mu }^{\prime }}_3=\frac{{\left(\theta +1\right)}^2\left({\theta }^3+8{\theta }^2+24\theta +24\right)}{{\theta }^3\left({\theta }^2+3\theta +1\right)}$ (4.4)
${{\mu }^{\prime }}_4=\frac{{\left(\theta +1\right)}^2\left({\theta }^4+16{\theta }^3+78{\theta }^2+168\theta +120\right)}{{\theta }^4\left({\theta }^2+3\theta +1\right)}$ (4.5)

Estimation of parameter of ZTPD

Maximum likelihood estimate (MLE): Let $x_1,x_2,\mathrm{...},x_n$  be a random sample of size $n$ from the ZTPD (2.1.1). The MLE $\widehat{\theta }$  of $\theta$ of ZTPD (2.1.1) is given by the solution of the following non linear equation.
 $e^{\theta }\left(\overline{x}-\theta \right)-\overline{x}=0$ , where$\overline{x}$ is the sample mean

Method of moment estimate (MOME): Let $x_1,x_2,\mathrm{...},x_n$ be a random sample of size $n$ from the ZTPD (2.1.1). Equating the first population moment about origin to the corresponding sample moment, the MOME $\tilde{\theta }$ of $\theta$ of ZTPD (2.1.1) is the solution of the following non linear equation.
$e^{\theta }\left(\overline{x}-\theta \right)-\overline{x}=0$ , where $\overline{x}$ is the sample mean
Thus both MLE and MOME give the same estimate of the parameter $\theta$ of ZTPD (2.1.1).

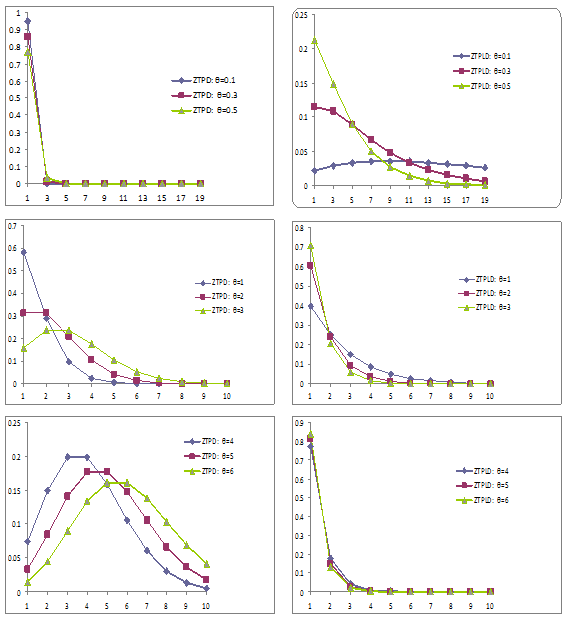
Figure 1 Graph of probability functions of ZTPD and ZTPLD for different values of their parameter. The left hand side graphs are for ZTPD and right hand side graphs are for ZTPLD.

Estimation of parameter of ZTPLD

Maximum likelihood estimate (MLE): Let $x_1,x_2,\mathrm{...},x_n$ be a random sample of size $n$ from the ZTPLD (2.2.1) and let $f_x$ be the Observed frequency in the sample corresponding to $X=x(x=1,2,3,\mathrm{...},k)$ such that ${\displaystyle \sum _{x=1}^k{f}_x}=n$ , where$k$  is the largest observed value having non-zero frequency. The likelihood function $L$ of the ZTPLD (2.2.1) is given by
$L={\left(\frac{{\theta }^2}{{\theta }^2+3\theta +1}\right)}^n\frac{1}{{\left(\theta +1\right)}^{{\displaystyle \sum _{x=1}^{k}x{f}_x}}}{{\displaystyle \prod _{x=1}^k\left(x+\theta +2\right)}}^{f_x}$  (5.1.1)
The log likelihood function is given by
$\log L=n\log \left(\frac{{\theta }^2}{{\theta }^2+3\theta +1}\right)-{\displaystyle \sum _{x=1}^{k}x{f}_x\log \left(\theta +1\right)}+{\displaystyle \sum _{x=1}^k{f}_x\log \left(x+\theta +2\right)}$
and the log likelihood equation is thus obtained as
$\frac{d\log L}{d\theta }=\frac{2n}{\theta }-\frac{n\left(2\theta +3\right)}{{\theta }^2+3\theta +1}-\frac{n\overline{x}}{\theta +1}+{\displaystyle \sum _{x=1}^k\frac{f_x}{x+\theta +2}}$
The maximum likelihood estimate $\widehat{\theta }$ of $\theta$ is the solution of the equation $\frac{d\log L}{d\theta }=0$ and is given by the solution of the following non-linear equation
$\frac{2n}{\theta }-\frac{n\left(2\theta +3\right)}{{\theta }^2+3\theta +1}-\frac{n\overline{x}}{\theta +1}+{\displaystyle \sum _{x=1}^k\frac{f_x}{x+\theta +2}}=0$  (5.1.2)
where $\overline{x}$ is the sample mean. This non-linear equation can be solved by any numerical iteration methods such as Newton- Raphson method, Bisection method, Regula –Falsi method etc. Ghitany et al.²⁰ showed that the MLE $\widehat{\theta }$  of $\theta$ is consistent and asymptotically normal.

Method of moment estimate (MOME): Let $x_1,x_2,\mathrm{...},x_n$  be a random sample of size $n$  from the ZTPLD (2.2.1). Equating the first population moment about origin to the corresponding sample moment, the MOME $\widehat{\theta }$  of $\theta$  of ZTPLD (2.2.1) is the solution of the following cubic equation.
$\left(\overline{x}-1\right){\theta }^3+\left(3\overline{x}-4\right){\theta }^2+\left(\overline{x}-5\right)\theta -2=0;\overline{x}>1$ , where $\left(\overline{x}-1\right){\theta }^3+\left(3\overline{x}-4\right){\theta }^2+\left(\overline{x}-5\right)\theta -2=0;\overline{x}>1$ is the sample mean. Ghitany et al.²⁰ showed that the MOME $\widehat{\theta }$  of $\theta$ is consistent and asymptotically normal.

In this section, both ZTPD and ZTPLD have been fitted to a number of data-sets using maximum likelihood estimates relating to demography, biological sciences, and social sciences to test their goodness of fits and it has been observed that in most of the cases ZTPLD gives much closer fits than ZTPD and in some cases ZTPD gives much closer fits than ZTPLD.

Mortality
Mortality does not depend only on biological factors; it depends upon the prevailing health conditions, medical facilities, the socio-economic and cultural factors. In developing and under-developed countries, the mortality among infants and children is found much higher than that among youngsters. The high infant mortality has thrown a serious challenge to the medical personnel and is considered as one of the sensitive position of existing medical and health facilities in the population.

In this section, an attempt has been made to test the suitability of ZTPD and ZTPLD in describing the neonatal deaths as well as of infant and child deaths experienced by mothers. The data-sets considered here are the data of Sri Lanka and India. The data-sets of Meegama et al.²¹ have been used as the data of Sri Lanka whereas the data from the survey conducted by Lal²² and the survey of Kadam Kuan, Patna, conducted in 1975 and referred to by Mishra²³ have been used as the data of India. It is obvious from the fittings of ZTPD and the ZTPLD that ZTPLD gives much closer fits in almost all cases except in Table 2. Hence, in case of demographic data, ZTPLD is a better alternative than ZTPD to model count data.

Biological sciences
In this section, an attempt has been made to test the goodness of fit of both ZTPD and ZTPLD on many data- sets relating to biological sciences. It has been observed that ZTPLD gives much closer fits than ZTPD in almost all cases except in Table 11 regarding the distribution of the number of leaf spot grade of Ichinose variety of Mulberry. Thus in biological sciences ZTPLD is a better model than ZTPD to model zero-truncated count data.

Social Sciences
In this section, an attempt has been made to test the goodness of fit test of both ZTPD and ZTPLD on many data-sets relating to social sciences, such as migration, Number of accidents and free-forming small Group size. It has been observed that the ZTPD gives much closer fits than ZTPLD in almost all cases except the distribution of the number of household having at least one migrant in Table 15.

In this paper, the nature and behavior of ZTPD and ZTPLD have been studied by drawing different graphs for the different values of its parameter. A general expression for the th factorial moment has been given and the first four moments about origin has been obtained. Also a very simple and easy method for finding moments of ZTPLD has been suggested. An attempt has been made to study the goodness of fit of both ZTPD and ZTPLD to count data relating to demography, biological sciences, and social sciences and it has been found that ZTPLD is a better model than the ZTPD in almost all data-sets relating to mortality and biological sciences whereas ZTPD is a better model than ZTPLD in almost all data-sets relating to social sciences.. Thus, ZTPLD has an advantage over ZTPD for modeling zero-truncated count data in mortality and biological sciences whereas ZTPD has an advantage over ZTPLD for modeling zer-truncated count data in social sciences.