The purpose of this study was to use a modified susceptible-exposed-infectious-recovered (SEIR) compartmental mathematical model to forecast the dynamics of the COVID-19 epidemic in the high and low pandemic cases that occurred in the State of Paraná, Brazil in 2021. Subsequently, the findings of this analysis were compared. The model parameters were adjusted based on official reports from the State of Paraná, Brazil. As a result, it can be observed that the parameters for susceptible population (S) and exposed population (E) tend to decay over time, with a more drastic drop for S and a slower decrease for E in high pandemics. Conversely, the parameter for infected population (I) tends to rise and decay over time, with a tendency to grow in high pandemics. Additionally, the parameter for recovered population (R) tends to rise over time, with a much higher growth rate in low pandemics than in high pandemics, as expected. The numerical simulation appears to align with reality, which is consistent with the scenario in various cities worldwide. Additionally, the implemented model has several advantages, including accurate adjustments despite the simplicity of the hypotheses and projections that are comparable to those of more complex models. The findings presented may provide useful suggestions for the prevention and management of COVID-19 outbreaks in different countries and regions.

Keywords: COVID-19 epidemic, epidemiological models, vaccine, SEIR model, spread and control, numerical simulation

The coronavirus disease 2019 (COVID-19), caused by SARS-CoV-2 (severe acute respiratory syndrome-coronavirus 2), has rapidly spread worldwide since December 2019, resulting in a significant number of infections and deaths globally. In Brazil, there have been a considerable number of deaths as of August 16, 2021, according to the COVID-19 Data Report from the Center for Systems Science and Engineering (CCSE) at Johns Hopkins University 2021.¹ According to the Paraná Health Secretariat,² as of September 13, 2021, Brazil has reported 20,999,779 infections and 586,851 deaths, with the state of Paraná accounting for 1,473,335 infections and 37,896 deaths. To address the spread of the virus, various control measures, including social distancing and mask-wearing, have been implemented by countries worldwide. Unfortunately, the virus has spread rapidly in recent months, leading to a shortage of hospital beds.

The vaccination process against COVID-19 is a crucial aspect of public health, and healthcare professionals are at the forefront of this effort. The use of licensed COVID-19 vaccines has shown promising results in preventing hospitalizations and fatalities caused by infectious diseases. Recent data suggests that these vaccines are playing a significant role in controlling the spread of the disease. According to the World Health Organization,³ until widespread vaccination is achieved, it is important for both vaccinated and unvaccinated individuals to be aware of the additional protective behaviors necessary to control the pandemic locally.

Vaccination has been proven to reduce deaths and severe illness from COVID-19, as well as transmission of the virus. Therefore, it is crucial to vaccinate as many people as possible and reduce the spread of the disease. It is important to consider vaccinating a significant proportion of the population, not only to protect those who receive the vaccine, but also to safeguard vulnerable individuals who cannot receive vaccines or remain at risk of infection even after vaccination. It is worth noting that failing to vaccinate widely may allow the virus to continue circulating.

The COVID-19 pandemic has been a significant challenge to global health and human life. Many epidemic models have been developed to assist world leaders and the World Health Organization in making decisions. In order to understand and analyze the epidemic trend, it is necessary to use parameter optimization algorithms to obtain the model mechanisms.

In the considered transmission model, the total human population is divided into four sub-compartments. The 'S' compartment represents the susceptible population, which is the section of the human population that can become infectious if exposed to the virus. The 'E' compartment denotes the exposed population, which represents the human population that is infected but not yet infectious or suspected to be infected. The term 'infected population' refers to individuals who have developed the full symptoms of COVID-19 and can transmit the virus to others through contact. It is important to note that this definition excludes individuals who are asymptomatic but still capable of spreading the virus. The section of the population that has fully recovered after treatment and is free from the disease is denoted by R. This has been discussed by various authors, including Yadava and Verma,⁴ Savioli et al.,⁵ Carcione et al.,⁶ Lopez and Rodo,⁷ Din and Algehyne,⁸ and Cintra and Fontinele.⁹

The following system of ordinary differential equations presents a transmission model for the COVID-19 pandemic.

$\frac{dS}{dt}=-\frac{\beta SI}{N}$   (1)

$\frac{dE}{dt}=\frac{\beta SI}{N}-aE$   (2)

$\frac{dI}{dt}=aE-\gamma I$   (3)

$\frac{dRt}{dt}=\gamma I$   (4)

The dynamical system of equations describes the rate of disease transmission between exposed and susceptible individuals as β, and between infected and susceptible individuals as α. The average disease incubation period is denoted by α − 1, while γ represents the rate of recovery and infectious period as γ − 1. Figure 1 shows a schematic diagram of the transmission model for the COVID-19 pandemic.

Figure 1 A schematic diagram showing the transmission model for COVID-19 pandemic.

The basal reproduction rate or basic reproduction ratio, $R_t$ is a crucial parameter in any epidemic. It is the classical epidemiological measure associated with the reproductive power of the disease, defined as the growth rate times the time of infection.⁶ (Carcione et al. [6]).

$R_t=b/\alpha$   (5)

If $R_t$  is greater than 1, the epidemic will experience exponential growth at the beginning of the contagious process. If $R_t$ is less than 1, the epidemic will experience exponential attenuation until it ends. Therefore, $R_t$ is a crucial parameter for controlling epidemics.

To study the effectiveness of vaccines in the state of Paraná, Brazil in 2021, numerical simulations were conducted. The simulations compared the high contamination rate in February, when the vaccination percentage was low, to the low contamination rate in September, when a high percentage of people were vaccinated. To conduct the simulation, we used data from the Paraná Health Department² and Ministério da Saúde Secretaria de Vigilância em Saúde.¹⁰

The data for February 20, 2021 is as follows: $I_o\left(confirmed\right)$ 607,632, initial number of infected individuals, $R_o$ - 449.980 recovered individuals, and $E_o$ (notified or suspected) is 1,529,476, initial number of exposed individuals. The population number of the State of Paraná is N=11,516,840. Therefore, $S_o=N-E_o-I_o-R_o$ =8,929,752, which is the initial number of susceptible individuals. The baseline reproduction index, $R_t$ is calculated as 1.5 with an α value of 1/5.2 [day^-1]. Using the formula $R_t=\beta /\alpha$ , we can determine that β=1.5/5.2 [day^-1]. The recovery rate, γ, is calculated as 1/D [day^-1], where D is the average duration of recovery. According to George,¹¹ Lauer et al.,¹² and Rees et al.,¹³ the average recovery duration is 10 days, which is used in this paper. As of the current date, 8,006,419 people have been vaccinated, resulting in a vaccination proportion of $\delta =277,707/N=0.024$ .

Meanwhile, as of September 13, 2021, there were 1,473,335 confirmed cases of infection ($I_o$ ), 1,382,448 cases of recovery ($R_o$ ), and 5,005,082 cases of exposure ($E_o$ ) in the State of Paraná, with a total population (N) of 11,516,840. Therefore, the initial number of susceptible individuals ($S_o$ ) is 4,905,975. The baseline reproduction index, $R_t$ is calculated as 0.8 with α=1/5.2 [day^-1]. Since, $R_t=\beta /\alpha$ we can calculate β as 0.8/5.2 [day^-1]. As of the reported data,² the number of vaccinated individuals is 8,006,419, resulting in a vaccination proportion of $\delta =0.695$ .

Next, we present the results and discussion of the numerical simulation of the COVID-19 epidemic using the susceptible-exposed-infectious-removed (SEIR) model. The model parameters were calibrated using the officially reported data from the State of Paraná, Brazil, considering both high and low pandemic scenarios.²

The simulation utilized Equations 1-5 and their corresponding parameters as defined in Din R et al.⁸ from the previous section. It was conducted to model the scenario where the population of the state of Paraná-Brazil had a low vaccination rate (2.4%) in February 2021.² The results of the simulation for a 30-day period are presented in Figure 2. The baseline reproduction index was set to $R_t=1.5$ , as per Parana Health Secreteriat² indicating a high level of contagion during a severe pandemic. Figure 2 shows that susceptibility (S) decreases drastically over time. Exposure (E) declines slowly, with a slight increase after five days and a subsequent slight decrease after 15 days. The infectious process (I) grows exponentially until it reaches a maximum at 25 days, after which it decreases slowly. Thus, the numerical simulation demonstrates a high infection rate during the peak of the pandemic and with a low vaccination rate, which is consistent with the reality of hospitals lacking beds and the population being forced into lockdown. However, the recovery rate grew almost linearly and had a high growth rate in relation to the contamination rate, which may have been influenced by the vaccination rate and lockdown measures.

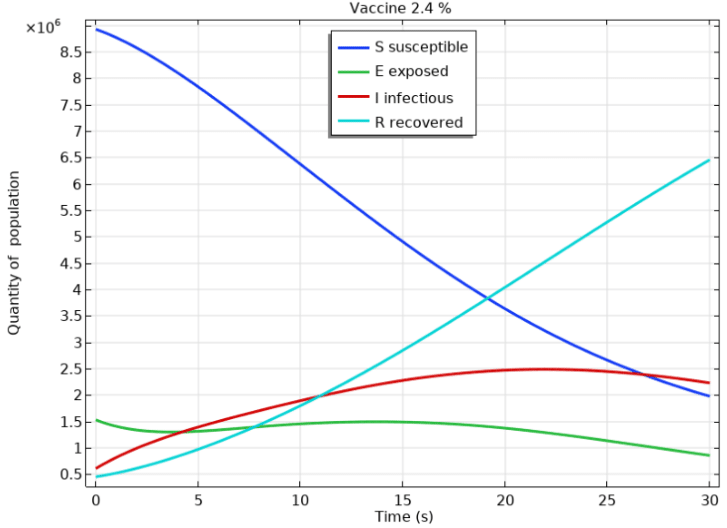
Figure 2 Shows a numerical simulation of the COVID-19 epidemic using the SEIR model for a severe pandemic case.

According to Parana Health Secreteriat² for the case with a 69.5% vaccine and a baseline reproduction index of $R_t$ =0.8 (indicating low contamination), Figure 3 shows a rapid decay of susceptibility (S) over time. It is important to note that the initial conditions for Figure 3 are different from those in Figure 2, where the drop is more drastic. Furthermore, the Exposure (E) also decays rapidly relative to S, but this drop is more abrupt compared to the same parameter in Figure 2. The infection parameter (I) rises quickly in the first few days, then gradually decreases until the end of the period. This parameter exhibits a similar trend to that in Figure 2, where it increases over time. The numerical simulation is consistent with the COVID-19 event, as the high pandemic trend justifies the obtained result. The language used is clear, objective, and value-neutral, with no biased or emotional language. The text is free from grammatical errors, spelling mistakes, and punctuation errors. The content of the improved text is as close as possible to the source text, with no additional aspects added. Additionally, the parameter recovery (R) shows a drastic increase, which is much higher than in Figure 2. This indicates that at low pandemic levels, the recovery rate is much higher.

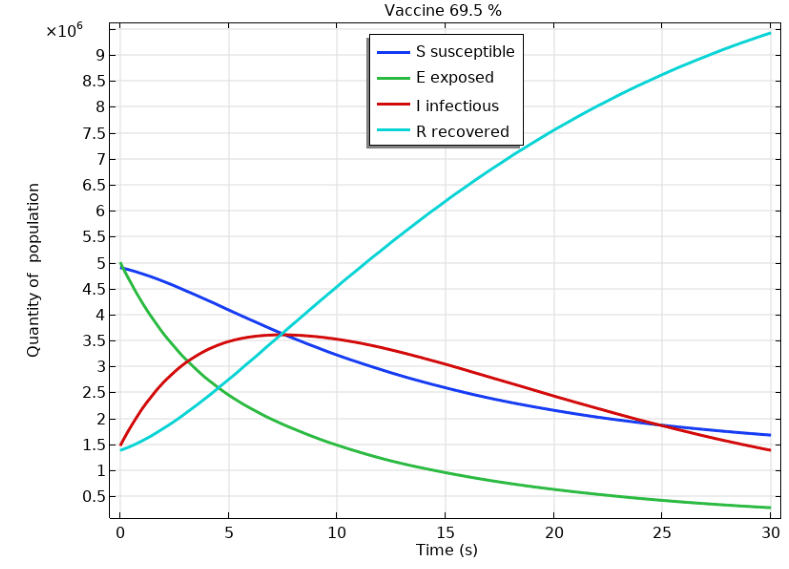
Figure 3 Displays a numerical simulation of the COVID-19 epidemic using the SEIR model for a case with a 69.5% vaccination rate.

The results of this work were comparable to those of Yadava and Verma,⁴ Savioli et al.,⁵ Carcione and Santos,⁶ Lopez and Rodo.⁷ The presented result is approximately consistent with the officially reported data from the State of Paraná, Brazil.² To achieve a more accurate simulation of reality, the data provided by health agencies needs to be more precise. However, this model did not take into account factors such as confinement, social distancing, lockdowns, psychological impacts, the emergence of new virus mutations, and emotional aspects. We will continue to study and refine the model. The objective of this task is to comprehend the mechanisms and phenomenology of the emergence of new coronavirus variants, as well as their spread and control.

The model parameters were calibrated using officially reported data from the State of Paraná, Brazil, for both high and low pandemic scenarios of the COVID-19 virus. The parameters for susceptible population (S) and exposed population (E) decayed as a function of time, with a drastic drop for S and a slower decrease for E in the high pandemic scenario. However, the parameter for infected population (I) rose and decayed as a function of time, with a tendency to grow in the high pandemic scenario. However, the R parameter for the recovered population increases over time. In low pandemics, this parameter exhibits much higher growth behavior than in high pandemics, as expected. Therefore, the numerical simulation is consistent with reality.

The current outcome aligns with the situation in various cities and countries worldwide. This is due to a significant percentage of the population being vaccinated, resulting in a decrease in lockdown measures. Additionally, schools, colleges, some universities, and government employees have resumed in-person activities, while companies are returning to normal operations. Although some individuals are wearing fewer masks, and more people are traveling, it is important to continue following safety guidelines. Our COVID-19 modeling predicts encouraging results: fewer infections and more recoveries worldwide.

The implemented model has several advantages. Firstly, despite the simplicity of the hypotheses, the adjustments obtained were quite accurate. Secondly, the projections made do not differ much from those of more complex models. Additionally, the instantaneous increment of cumulative diagnosed people depends on the history of cumulative infected people, which takes into consideration the latent period.

The results may offer valuable recommendations for preventing and managing COVID-19 outbreaks in various regions and nations.

It is important to exercise caution when interpreting the results at this stage of the epidemic, as small variations in observed data can lead to significant changes in trends. Despite this limitation, the substantial increase in cases indicates that the findings are robust.

Overall, the model appears to be stable, as demonstrated by the uncertainty analysis. Additionally, the updated parameters align closely with the actual reported data, indicating the initial projections of the model were not significantly off. This adds value to the work and supports the previous discussion.

Models are utilized to predict and comprehend the spread of infectious diseases and the factors that affect their dynamics. It has been clear to scientists for many decades that quarantine, social distancing, and strict health and safety standards are essential to stop the spread of a virus, even if the predictions are inaccurate. Quarantine was even implemented in medieval times to fight the black death before the existence of viruses was known. The pandemic has revealed the failure of policy-makers. Basic modeling results show that earlier adoption of measures can save thousands of lives and prevent the pandemic. The interface of science, society, and politics remains uneasy, even in highly developed countries, indicating a disregard for scientific evidence. Additionally, one of the consequences is that some of these countries do not invest enough in research and development and must acquire new technology from overseas at a much higher cost

None.

The authors declare there is not any conflict of interest.

None.

1. Johns Hopkins University (2021) COVID-19 Data Report from the Center for Systems Science and Engineering (CCSE).
2. Paraná Health Secretariat. Coronavirus(COVID-19). Secreteria Da Suade. 2021.
3. World Health Organization (W.H.O). Statement for healthcare professionals: How COVID-19 vaccines are regulated for safety and effectiveness (Revised March 2022). 2021.
4. Yadava RP, Verma R. A numerical simulation of fractional order mathematical modeling of COVID-19 disease in case of Wuhan China. Chaos Solitons Fractals. 2020;140:110124.  
5. Savioli GB, Carcione JM, Santos JE, et al. A numerical simulation of the COVID-19 epidemic in Argentina using the SEIR model. Latin American Applied Research. 2021;51(3):179–184.
   
6. Carcione JM, Santos JE, Bagaini C, et al. A simulation of a COVID-19 epidemic based on a deterministic SEIR model. Front Public Health. 2010;8:230.
   
7. Lopez L, Rodo X. A modified SEIR model to predict the COVID-19 outbreak in Spain and Italy: simulating control scenarios and multi-scale epidemics. Results in Physics. 2021;21:103746.
   
8. Din R, Algehyne EA. Mathematical analysis of COVID-19 by using SIR model with convex incidence rate. Results in Physics. 2021;23:103970.
9. Cintra HPC, Fontinele FN. Estimative of real number of infections by COVID-19 in Brazil and possible scenarios. Infectious Disease Modelling. 2010;5:720–736.
   
10. Ministério da Saúde Secretaria de Vigilância em Saúde. 2021.
11. George N, Tyagi NK, Prasad JB. COVID-19 pandemic and its average recovery time in Indian states. Clinical Epidemiology and Global Health. 2021;11:100740.
    
12. Lauer SA, Grantz BA, Bi Qifang MHS, et al. The incubation period of coronavirus disease 2019 (COVID-19) from publicly reported confirmed cases: estimation and application. Ann Intern Med. 2020;172(9):577–582.
13. Rees EM, et al. COVID-19 length of hospital stay: a systematic review and data analysis. BMC Med. 2020;18(1):1–14..