Recently, Markov chain Monte Carlo (MCMC) estimation method is explosively popular in a variety of latent variable models including those in structural equation modeling (SEM). In the SEM framework, different MCMC approaches developed according to choices in the construction of the likelihood function as may be suitable for different types of data. However, despite their theoretical appeal over traditional estimation routines, the features and differences between various types of SEM MCMC approaches are not well understood. In this paper, two major MCMC approaches (i.e., the moment-level data approach and the subject-level data approach) are compared using two a two-factor model with a directional path on real data sets.

Keywords: structural equation modeling, markov chain monte carlo, parameter estimation, bayesian inference

Structural equation modeling and traditional estimation algorithms

Structural equation modeling¹ has been used in a variety of research applications in the social and behavioral sciences. A broad-spectrum aim of SEM can be expressed as testing the hypothesis that the population-level covariance matrix for a set of measured indicator variables is equal to the model-implied covariance matrix based on the hypothesized factor model. And, this relationship can be expressed as Σ = Σ(θ) where Σ represents the population covariance matrix of a set of observed indicator variables and Σ(θ)   represents the model implied covariance matrix as a function of θ, a vector of model parameters.

Assuming multivariate normality of the observed variables, common parameter estimation routines, including maximum likelihood,¹ normal theory generalized least square,² and weighted least squares method³ can provide consistent, efficient, and unbiased parameter estimates and asymptotic standard errors along with an omnibus test of model fit if sample size is adequate, and the model is properly specified (Bollen,¹ for more details of these estimation routines). 

All of these traditional model parameter estimation procedures involve a numerical search algorithm using the first and/or second derivatives of the target function to minimize.⁴ These estimation methods are known as gradient-based or Newtonian search algorithms: using the first and/or second derivatives, the algorithm iteratively searches the parameter estimates by minimizing (or maximizing) the target function (for more details of the general gradient-based search algorithms, see Süli & Mayers;⁵ for more specific SEM application of the gradient-based search algorithms, see Lee,⁴).

A traditional estimation algorithm (e.g., ML) seeks the global maximum of the fit function and is analogous to climbing a mountain where the final goal is to arrive at the highest peak of the mountain. A noteworthy challenge of this traditional estimation algorithm is the fact that there might be multiple hilltops that appear to be the highest peak of the mountain, and that the search may lead to on of these points. This is the well known problem of local maxima. Problems associated with non-convergence or convergence to local maxima tend to worsen as sample size decreases³ and/or the model is complex (e.g., missing data and/or non-normal data; Lee,⁴). Because it is common in social and behavioral research to analyze data from small samples (e.g., less than 100) and substantive theories often dictate the propriety of a more complex hypothesized model, these disadvantages of traditional estimation routines may limit the application of SEM in applied research.

Simulation based estimation 

Recently, simulation-based estimation methods known as Markov chain Monte Carlo (MCMC) techniques have drawn an increasing amount of attention in statistical modeling. MCMC provides a virtually universal tool to deal with integration or optimization problems.^6-8 MCMC estimation approaches have been shown to have methodological advantages in SEM, including reliable parameter estimation with small samples, flexibility of handling missing data, modeling ordinal data, nonlinear relationships, and finite mixture models.^4,9-13

Although the technical advantages of MCMC over the traditional methods have been advocated for some time, the details of MCMC estimation are not widely understood among SEM researchers, in part because of the variety of MCMC algorithms, computational complexity, and a host of technical matters involved in running MCMC estimation (e.g., determination of the numbers of simulation iterations, configuration of Markov chains for fast convergence; Gilks, et al.,¹⁴). This is in part due to the lack of detailed illustrations in the literature of this algorithm for SEM.¹⁵ The implementation of MCMC algorithms requires efficient computational strategies, as well as SEM-specific choices for various technical components (e.g., determination of the numbers of simulation iterations, configuration of Markov chains for fast convergence; Gilks, et al.,¹⁴). One choice that may lead to differences in performance of the algorithm involves the construction of the likelihood function. In SEM, we may employ a likelihood function based on either the subject-level data or moment-level data. However, there is a relative absence of methodological points. This is the well known problem of local maxima. Problems associated with non-convergence or convergence to local maxima tend to worsen as sample size decreases³ and/or the model is complex (e.g., missing data and/or non-normal data; Lee,⁴). Because it is common in social and behavioral research to analyze data from small samples (e.g., less than 100) and substantive theories often dictate the propriety of a more complex hypothesized model, these disadvantages of traditional estimation routines may limit the application of SEM in applied research. 

Simulation based estimation 

Recently, simulation-based estimation methods known as Markov chain Monte Carlo (MCMC) techniques have drawn an increasing amount of attention in statistical modeling. MCMC provides a virtually universal tool to deal with integration or optimization problems.^6-8 MCMC estimation approaches have been shown to have methodological advantages in SEM, including reliable parameter estimation with small samples, flexibility of handling missing data, modeling ordinal data, nonlinear relationships, and finite mixture models.^4,9-13

Although the technical advantages of MCMC over the traditional methods have been advocated for some time, the details of MCMC estimation are not widely understood among SEM researchers, in part because of the variety of MCMC algorithms, computational complexity, and a host of technical matters involved in running MCMC estimation (e.g., determination of the numbers of simulation iterations, configuration of Markov chains for fast convergence; Gilks, et al.,¹⁴). This is in part due to the lack of detailed illustrations in the literature of this algorithm for SEM.¹⁵ The implementation of MCMC algorithms requires efficient computational strategies, as well as SEM-specific choices for various technical components (e.g., determination of the numbers of simulation iterations, configuration of Markov chains for fast convergence; Gilks, et al.,¹⁴). One choice that may lead to differences in performance of the algorithm involves the construction of the likelihood function. In SEM, we may employ a likelihood function based on either the subject-level data or moment-level data. However, there is a relative absence of methodological literature that illustrates the properties and differences of these new developments in MCMC estimation for SEM. Consequently, researchers interested in choosing MCMC methods in SEM may encounter difficulties in understanding and/or selecting an appropriate MCMC approach according to their own research scenario. 

The main purpose of this paper is to illustrate the two major SEM MCMC approaches (i.e., the moment-level data approach and the subject-level data approach). A subject-level approach estimates a model with raw response data. The moment-level approach estimates a model with summary statistics as data. This latter approach is based on the familiar Wishart probability density distribution,¹ which is also at the root of the well-known maximum likelihood (ML) fit function for SEM. We also show how the moment-level MCMC method reduces computational loads and simplifies the MCMC process as compared to the subject-level approach. A comparison of estimates by traditional ML, the moment-level MCMC approach, and the subject-level MCMC approach within the context of examples are provided. 

Background and theoretical framework

Markov chain monte carlo estimation in structural equation modeling: Recently, MCMC approaches have received much attention in SEM as an alternative that overcomes limitations of the gradient-based traditional estimation methods.⁴ MCMC methods constitute an extremely flexible approach to estimate the parameters of complex multivariate systems that are impossible to solve in closed form or even difficult to numerically solve by the traditional estimation methods. MCMC can (a) provide an exhaustive exploration of a complex high-dimensional parameter space of random variables, (b) partition the joint densities into a set of marginal densities of parameters of interest, and (c) yield the density of any additional parameter as a function of those model parameters. Furthermore, its flexibility allows MCMC to accommodate complex models such as those with nonlinear effects,¹⁰ mediation effect analysis,¹⁶ coefficient alpha,¹⁷ Polychoric correlation,¹⁸ and discontinuous and/or ordered categorical data.¹⁹ 

MCMC also allows us to explicitly investigate the sensitivity of prior distributions for parameters when used in the context of Bayesian inference. Because MCMC algorithms are designed to empirically sample from a target density of parameters of interest, this method naturally aligns with the Bayesian perspective on statistical inference in which parameters are treated as random variables.

Although these methodological advantages of new estimation methods in SEM have been demonstrated in the last decade,^11-20 for more details of advantages of Bayesian approach over the traditional estimation methods), the fundamentals and technical details of these new developments are not well understood. For the purpose of illustrating these new developments, we discuss MCMC estimation in terms of two facets that researchers face when employing MCMC for SEM: the mechanics of the sampling algorithms and the likelihood function. 

Overview of MCMC sampling algorithms

MCMC is a Monte Carlo simulation based estimation method which empirically samples from a possibly complex multivariate distribution, often by strategically decomposing the joint distribution into more manageable univariate or smaller multivariate densities using Markov chain property. The MCMC approach simultaneously samples from one or more dimensions of a target distribution while moving throughout the support of the distribution.¹⁴ The term “Monte Carlo” is in reference to the nature of random simulation process the while “Markov chain” refers to the process whose property is that future states are independent of the past states given the present state. This process creates a set of univariate or smaller multivariate chains of values that are samples of values drawn from the target distribution. The target distribution needs to be specified only up to a constant of proportionality. This makes MCMC well suited to estimation in Bayesian approaches to SEM and other latent variable models in which analytical solutions to posterior distributions are often intractable.^21,22 In such cases, the Markov chain is constructed so that the target distribution is the posterior distribution of the unknown entities in the model. 

A key component of MCMC estimation is the sampling algorithm to generate samples from the target distribution. Among the dozens of MCMC sampling algorithms that have been developed over last three decades, the Metropolis algorithm or and its extension to the Metropolis-Hastings algorithm are the most popular algorithms^23,24 for the original introduction; see Gilks, Richardson, & Spiegelhater,¹⁴ for a presentation of various hybrid Metropolis algorithms). An advantage of using the Metropolis type of algorithm over other MCMC algorithm is that it is easy to implement when sampling from multivariate distributions. Specifically, the structure of this algorithm is fairly simple and does not involve complex numerical procedure such as adapting an enveloping function required in rejection sampling method.¹⁴ 

Overview of metropolis algorithm

Let g(θ) denote a distribution of interest that we wish to sample from. In the Bayesian framework, this may be more fully denoted as the posterior distribution g(θ|Y) where Y is observed data. For the simplicity of presentation, we will denote g(θ|Y) as g(θ) through this paper. The Metropolis algorithm for SEM can then be more formally described in a series of six steps that comprise one iteration of the algorithm:

Step 1: Establish the set of starting values for the parameters: θ ^j=0

Step 2: Set j = j + 1, and draw sample a set of candidate values, θ^c, from a set of symmetric proposal distributions denoted by q(θ^c | θ ^j-1)

Step 3: Compute the ratio {g(θ ^c)/g(θ ^j-1) and determine whether it is smaller or larger than 1. Choose the smaller of the two and denote it by α.

Step 4: Draw a random value u from a uniform distribution defined over (0,1). 

Step 5: Compare α with u. If α > u, then set θ ^j= θ ^c, otherwise, set θ ^j= θ ^j-1. 

Step 6: Return to the step 2 until enough candidate values are sampled.

In simple terms, at each MCMC iteration, the Metropolis algorithm takes the current estimate of each parameter value (θ^j-1) and compares it to a plausible candidate (θ^c), which is drawn from a so-called proposal distribution (q) which is symmetric with respect to its arguments. If the proposed value is more likely than the current value it is chosen as the next value for the parameter (θ^j-1); if it is less likely, the proposed value will be accepted with some probability α. 

The major computational step in the algorithm is the computation of the ratio (i.e., the Metropolis ratio) of the two target distribution values at θ^c and θ ^j-1, which are denoted by g(θ^c) and g(θ ^j-1), respectively. Furthermore, in a Bayesian framework, this target distribution is the posterior distribution which is proportional to L(θ)×P(θ), where L(θ) is a SEM likelihood function and P(θ) is the set of prior distributions for θ. In other words, this computation of the Metropolis ratio is determined by a SEM likelihood function L(θ) and the prior distribution P(θ). If one adopts a non-informative prior distribution (over all parameters), the Metropolis ratio effectively reduces to the ratio of the two likelihood function values at θ ^c and θ ^j-1, denoted by L(θ ^c) and L(θ ^j-1), respectively.

The incorporating the prior distribution is a distinctive advantage of the Bayesian approach over the traditional approaches (see e.g., Scheines et al.,¹¹). However, critics also have noted that improperly specified prior distributions can compromise the veracity of the results (Jeffereys,²⁵ or Edwards,²⁶ for more discussion on the criticism on the use of prior). The current work employs suitable diffuse prior distributions to (a) illustrate the similarity of the results of MCMC estimation to that of traditional estimation approache under diffuse priors and (b) properly focus on the principles of and choices of estimation that concern the likelihood function. Specifically, we consider two major approaches to construct the likelihood function in SEM, and illustrate the implications of the differences between two approaches. 

After computing the ratio α, the third step involves comparing the value of the ratio to 1 and choosing the value that is smaller amongst the two. Note that the value of 1 indicates that the proposed and the current value are either equally likely (i.e., L(θ ^c) = L(θ ^j-1) or the proposed value is more likely than the current value (i.e., L(θ ^c) > L(θ ^j-1) while a value of the ratio smaller than 1 indicates that the proposed value is less likely than the current value (i.e., L(θ ^c) < L(θ ^j-1). 

Since the Metropolis algorithm simulates a random sample from the posterior distribution under Markov chain properties, a proposed value that is less likely than a current value is not automatically discarded. Whether a proposed value that is less likely is accepted is decided by a random draw. Specifically, after randomly drawing a value u from a uniform distribution defined over the interval (0,1) one needs to compare α and u to decide whether the proposed value should be accepted. If α  is greater than the value for u, the proposed value is accepted as the j^th iteration value for θ; if α is smaller than the value for u, the current parameter value is accepted as the j^th iteration value. Thus, proposed values that are at least as likely as current values are always accepted whereas proposed values that are less likely than current values are sometimes accepted in accordance with a random process. This randomness of the selection process is essential to make sure the chain (a) does not get stuck on one or multiple value(s), and (b) exhaustively searches entire possible value range of the parameter. That it, is essential to ensure that the chain converges to the target distribution of interest.¹⁴ 

The Metropolis algorithm has been further generalized to the case of a non-symmetric proposal distribution, i.e., the Metropolis-Hastings algorithm (Hastings,²⁷). By the nature of some SEM parameters, e.g., error variances, symmetric proposal distribution (e.g., Gaussian proposal ranges from – ∞ to + ∞) may not be relevant. In such cases, an asymmetric proposal distribution (e.g., log-Gaussian rages from 0 to + ∞) might be more appropriate, and the Step 3 ratio (the Metropolis-Hastings ratio for this case) computation becomes more complex than that of Metropolis algorithm. Technical details of this algorithm are beyond scope of this paper; Gilks et al.,¹⁴ or Lynch.²⁸

Choices in implementing mcmc estimation with the metropolis or metropolis-hasting algorithm

There are three critical places within the algorithm that impact its efficiency for a particular application. These are (a) choosing the starting values in step 1, (b) choosing the proposal distribution for use in step 2, and (c) choosing the length of the cycle to end after step 6 at some point in time. 

In one respect, the choice of the starting values for the parameters is not a critical issue because MCMC theory states that the distribution produced by the Markov chain will converge to the target distribution of interest irrespective of the chosen starting value.²⁹ However, poorly chosen starting values may cause the algorithm to require more iterations before it converges (i.e., it requires a longer burn-in period), which results in longer MCMC run times. Therefore, even though the choice of starting values is irrelevant from a theoretical perspective, it is critical from a practical perspective. Choi,³⁰ for more detail discussion of the starting value issue for the Metropolis algorithm in the context of SEMs.

Another key choice in the Metropolis (or Metropolis-Hasting) algorithm is the choice of the proposal distribution in the second step. Interestingly, the convergence of a Markov chain formed via a Metropolis sampler to the posterior distribution does not depend on the shape of proposal distribution, subject to broad regularity conditions (e.g., that the proposal distribution is symmetric for Metropolis algorithm, that it is defined over the support of the posterior; Gilks et al.,¹⁴). Yet, just as with the choice of starting values above, the choice of proposal distribution shape is practically important because it determines how quickly the chain converges to the posterior distribution. Choi et al.,³¹ illustrated the impact of the choice of a proposal distribution in terms of its jump size on the convergence of Metropolis algorithm using a popular SEM example. This article shows the Metropolis algorithm converges quickly only when the jump size is optimally chosen (for the jump size issue in the context of Item Response Theory model, Levy,³²). In other words, the efficiency of the Metropolis algorithm in practice depends on this choice of proposal distribution. Many researchers have focused on the choice of the proposal distribution or dynamically-update the proposal distribution of the Metropolis or Metropolis-Hastings algorithm, which are referred to as hybrid Metropolis algorithms (Gilks et al.,¹⁴). The software package employed in the current work, AMOS 7.0 (Arbuckle,³³) adopts Metropolis-Hastings algorithm with an adaptive algorithms, optimally selects the proposal distribution parameter, e.g., jump size. For a more detailed discussion of the proposal distribution characteristic (i.e., jump size) issue for the Metropolis algorithm in the context of SEMs, Choi.³⁰

The third choice in the Metropolis algorithm pertains to the length of the estimation cycle. Theoretically, an MCMC estimation requires sufficiently many iterations (i.e., MCMC runs or MCMC cycles) to fully converge to the posterior distribution but, of course, in practice the cycle has to be stopped at some point. The algorithm is stopped when a sample is obtained that is large enough to provide an accurate estimates (i.e., point and interval) of the parameter. Therefore, given the requirement of a large number of MCMC iterations, it is important to consider the computational load in the evaluating the likelihood function, as that has a large impact on the overall computational time of MCMC estimation. A frequently advanced criticism of the use of MCMC estimation in practice is the estimation time necessary to reach convergence of the chains and adequately sample from the target distribution. As discussed below, the differences in computational load plays a central role in the distinction between the alternative approaches in constructing the likelihood. 

This length of estimation cycle is also related to a determination of the point in the Markov chain after which chain has reached its stationary distribution and seems to behave consistently (i.e., the point at which the burn-in period ends), which can only be roughly gauged based on plots. The samples before this point are recommended to be discarded and the samples after this point are selected as samples from the posterior distribution. It is important to note, though, that there may be dependencies amongst the sampled points due to the way the algorithm functions for a particular SEM so that not every observation may be sampled in practice.

Overview of gibbs sampling algorithm

Another popular MCMC algorithm is the Gibbs sampler (Gelfand & Smith;³⁴ Geman & Geman,³⁵). Suppose that the parameter vector of interest is $\theta =({\theta }_1,\dots ,{\theta }_p)$ where p is the number of SEM parameters of interest. The Gibbs sampling algorithm can then be more formally described in a series of three steps that comprise one iteration of the algorithm:

Step 1: Establish the set of starting values for the parameters: θ ^j=0

Step 2: Set j = j + 1, and draw sample a value, θ, from each conditional distribution:

$\begin{array}{c}g\left({\theta }_1\right|{\theta }_2,\dots ,{\theta }_p,Y)\\ g\left({\theta }_2\right|{\theta }_1,{\theta }_3,\dots ,{\theta }_p,Y)\\ \dots \\ g\left({\theta }_p\right|{\theta }_1,\dots ,{{\theta }_p}_{-1},Y)\end{array}$

Step 3: Return to the step 2 until enough values are sampled.

In simple terms, at each iteration, the Gibbs sampling algorithm samples each parameter value from the conditional distribution of each parameter given all other entities. The Gibbs sampler may be viewed as a special case of the Metropolis sampler in which every candidate value is accepted. From this perspective, the conditional distributions are the proposal distributions of the Metropolis algorithm and the Metropolis ratio is always 1. The rationale behind Gibbs sampling algorithm is that it is possible to sample from the joint posterior distribution by successfully sampling individual parameters from the set of p conditional distributions (Lynch,²⁸). Therefore, this MCMC algorithm will sample one value of each individual parameter from respective conditional distributions during one MCMC iteration, i.e., one cycle of Gibbs sampling. According to the MCMC theory, under general conditions, the sampled values from this algorithm will converge to the target distribution of interest.^34,29

Choices in implementing mcmc estimation with the gibbs sampling algorithm

Similar to the Metropolis algorithm, although the Gibbs sampling algorithm is also conceptually relatively simple, however, there are also three critical places within it that impact its efficiency for SEM. These are (a) choosing the starting values in step 1, (b) setting up the conditional distributions for use in step 2, and (c) choosing the length of the cycle to end after step 3 at some point in time. Issues surrounding (a) the starting values and (c) the length of the cycle are essentially same to those of the Metropolis algorithm. Although the Gibbs sampling algorithm is free from the concerning on selecting and/or dynamically tuningproposal distribution characteristics, where the process differs is in the construction of conditional distributions. Therefore, in this section, we will focus on the issue of setting up the conditional distributions for parameters.

Lee illustrates the Gibbs sampling for standard SEM under certain choices of prior distributions with analytically derived conditional distributions for SEM parameters. More generally, it is mathematically challenging (or even impossible for some cases) to derive all conditional distributions and similarly computationally challenging to set up all conditional distributions into custom MCMC code in practice. 

One way of overcoming these challenges would be directly sampling from the target (i.e., posterior) distribution within the Gibbs sampling algorithm framework using an envelope function, so called the adaptive rejection sampling (ARS; Gilks et al.,¹⁴). In other words, this ARS method requires the full conditional distribution with parameters (the joint posterior distribution in the hierarchical setting for all parameters) instead all conditional distributions for parameters (Gilks et al.,¹⁴). There are several ARS algorithms according to the ways of developing an envelope function. For example, Ripley³⁵ proposed an envelope function based on the log of the target distribution (i.e., posterior distribution). This method involves the envelope function evaluations of which are often computationally very expensive in applications of Gibbs sampling. To overcome this computational cost in evaluating envelope function, Gilks and Wild³⁷ proposed a method of constructing the envelope from a set of tangents to the log-density. Such evaluations are typically very expensive computationally in applications of Gibbs sampling. Gilks³⁷ also proposed a method using secants intersecting on the log-density. These two methods assume that the log density is concave, which is usually true for most of social and behavioral statistical methods include SEMs. WinBUGS 1.4 (Spiegelhalter et al.,³⁸) employs Gibbs sampling with this ARS algorithm. Details of this program application for SEM will be illustrated in a later section of this paper.

Constructing the likelihood function for MCMC

Another key component of MCMC estimation in SEM is the likelihood function which determines the target distribution function. There are two major approaches to constructing the likelihood function, the moment-level (or summary-level) data approach and the subject-level (or raw-level) data approach. As discussed in details in the following subsections, these differ principally in the type of data involved. 

The moment-level (or summary-level) data approach 

The moment-level data approach constructs the likelihood function in terms of the sample variances and covariances in the covariance matrix S. This approach uses the familiar Wishart probability density function (Bollen, [1]; Mardia, et al.,³⁹):

$\frac{{\left|S\right|}^{(n^{\ast }-J-1)/2}\exp \left\{-(n^{*}/2)tr\left[{\mathbf{S\Sigma }}^{-1}\right(\theta )\right\}{(n^{*}/2)}^{J{n}^{*}/2}}{{\pi }^{J(J-1)/4}{\left|\mathbf{\Sigma }\left(\theta \right)\right|}^{n^{*}/2}{\displaystyle \prod _{i=1}^J\mathbf{\Gamma }\left[(1/2)(n^{\ast }+1-i)\right]}}$              (1) 

 where J is the rank of matrix Σ; n* is n, the sample size, – 1; Γ is a gamma function; S is a covariance matrix as observed data. This function is also at the root of the well-known maximum likelihood (ML) fit function for traditional SEM (Bollen,¹), as the likelihood function. Traditional statistical inference in SEM is based on probability models relating the observed covariance matrix, S, to the unknown parameters and the model-implied covariance matrix, Σ(θ). The Wishart distribution function based likelihood function, denoted LMoment (S|Σ(θ)) = W(S|Σ(θ)). This probability density function returns the probability of our data, S, given the model Σ(θ) that is composed of parameters θ, and p. In other words, this likelihood function summarizes the information about SEM parameters θ and may be defined as the conditional distribution of the data and taken as a function of θ.  Without a loss in generality, we will denote W(S|Σ(θ)) as W(S, Σ(θ)) and LMoment (S|Σ(θ)) as LMoment (S, Σ(θ)) throughout this paper.

Conceptually, ML estimates θ as unknown fixed points that maximize the likelihood function using the gradient-based iterative numerical algorithms. In contrast, the Bayesian approach (using MCMC estimation) treats θ as random and seeks the distributions of the parameters in θ given S. Specially, the target (or posterior) distribution of interest for this case g _Moment (θ) is proportional to L_Moment (S, Σ(θ))×P(θ) or W(S, Σ(θ))⋅Π(θ). Therefore, the major task of the moment-level data approach SEM MCMC algorithm is constructing a sampling algorithm to draw samples from W(S, Σ(θ))×P(θ). 

The gist of this approach is the nature of Wishart function based likelihood function takes the covariance matrix (S) as data. Consequently, in the implementation of MCMC, there are several methodological characteristics of this particular approach. First, because of the simple structure of the likelihood function, this moment-level data approach naturally goes well with the Metropolis algorithm; the Metropolis ratio is simply becomes 

g(θ ^c)/g(θ ^j-1) = {W(S, Σ(θ ^c)) ×P(θ ^c)} / {W(S, Σ(θ ^j-1)) ×P(θ ^j-1)}. Again, in case of non-informative priors for all parameters, the Metropolis ratio is simply ratio of two Wishart distribution values, i.e., W(S, Σ(θ ^c)) / W(S, Σ(θ ^j-1)). 

Second, this Wishart distribution based SEM likelihood function is very well known. Also, building the model implied covariance matrix given the structural equations can be easily implemented by matrix algebra (Bollen,¹). Therefore, the implementation part of this approach is quite straightforward.

Third, because the fact that this approach takes the covariance matrix, i.e., the second-order moments, as data, the numerical cost does not increase as sample size increases. A critical aspect of MCMC implementation is that it requires many iterations, and one of the key issue in the MCMC literature is reducing the computational time. So, consequently, the independence of the numerical cost of evaluating this likelihood function from the sample size is advantageous in light of the large number of iterations necessary for convergence and adequately sampling from the target distribution. Moreover, much of the SEM literature analyzes and reports results in terms of first- and second-order moments instead of raw data. Therefore, this MCMC estimation process that requires only summary-level data (i.e., the sample covariance matrix) is desirable.

Fourth, the use of the Wishart probability density function in constructing the likelihood follows from an assumption that the observed variables are normally distributed (Bollen,¹). Although ML parameter estimates under such assumptions are often robust to violations of normality, the estimates of the standard errors and the model χ² can be severely biased (Browne;⁴⁰ Yuan & Bentler,⁴¹). An extension of this approach to non-normally distributed data (including discrete data) is not straightforward. Although WLS (Browne,³) has been developed and been widely used to address this issue within the traditional gradient-based estimation paradigm, corresponding developments in MCMC estimation in SEM have not yet been developed for analyzing moment-level data.

Fifth, this approach can be implemented by the popular SEM software AMOS 7.0 (Arbuckle,³³). In AMOS, the researcher can specify, estimate, assess, and present a model using an intuitive path diagram to show hypothesized relationships among variables. AMOS also has many beneficial features on MCMC based Bayesian inference. Based on this program, users can easily investigate the posterior distribution (i.e., the converged target distribution), trace plot (the MCMC chain time-series plot utilized to assess convergence), autocorrelation plot (the autocorrelation plot of each MCMC chain to assess convergence and the serial dependence of values in the chain), and other detail MCMC options (maximum MCMC runs, number of burn-in, convergence criterion, thinning) through the user-friendly graphical interface (Arbuckle,³³ for more details of MCMC options). The default prior distribution in AMOS is uniform from -3.4*10^38 to -3.4*10^38) prior for all parameters. For all practical purposes, this prior is uniform over the values for parameters in SEM; as such, the target (posterior) distribution will essentially just be the normalized version of the likelihood function. Users can configure the prior distribution also through user-friendly graphical interface, so one can easily perform this kind of prior sensitivity analysis (Arbuckle,³³). In the illustration section of this paper, we will use AMOS 7.0 for the moment-level data approach.

The subject-level (or raw-level) data approach

Another way of constructing the likelihood involves specifying the conditional probability based on the subject-level observed data, Y. Let P(Y_ij | θ) denote the probability model for the observed value from subject i to measured variable j given the model parameters θ. In this formulation, the model parameters θ include the (unknown) values of the latent variables for each subject. These terms play a central role in the model construction in the subject-level approach. Specifically, by mean-centering the measured variables and following the usual assumptions of normality, independence of errors, and independence over subjects, P(Y_ij | θ) is specified as normally distributed where (a) the mean is obtained as the sum of the products obtained by multiplying the subject’s factor scores by the corresponding loadings for that measured variable, and (b) the variance is the error variance for that measured variable. The likelihood for the complete data is constructed by aggregating over measured variables and subjects as 

 L_Subject (Y |θ) = P(Y |θ) = $\prod _i\prod _{j}P\left(Y_{ij}\right|\theta )$ ,                    (2)

There are several methodological characteristics of this particular approach. First, because the likelihood function involves the product over subjects and measured variables, the numerical cost increases by sample size and/or the number of measured variables. To the extent that the MCMC process involves evaluating the likelihood at every iteration, and many iterations are necessary, such a procedure may require considerable estimation time. A related issue is the presence of the latent subject variables in this approach. In conducting MCMC at the subject-level, values for each subject’s latent variable will be drawn at each iteration in the MCMC process. If M is the number of latent variables, the subject-level approach requires that N×M more parameters need to be drawn at each iteration of the MCMC process in the subject-level approach as compared to the moment-level approach. Thus, MCMC estimation at the subject-level can be quite computationally expensive and time consuming. In addition, numerical problems may occur while computing the product of individual level probabilities. Furthermore, large numbers of parameters can worsen this situation. Therefore, this option may quickly become practically infeasible with large samples. The dependence of the numerical cost on sample size would be critical information for someone who is considering the subject-level data approach.

In contrast to the moment-level approach, this approach is versatile enough to be adapted to model non-normal or discrete data (Lee & Song;⁴² Lee & Zhu;⁴³ Shi & Lee,¹⁹). This methodological versatility of the subject-level approach should be appealing to researchers using complex models. Third, setting up the necessary conditional distributions or full conditional distributions may require considerable programming skill, especially as the model gets complex (e.g., with more increasingly complex relationships among factors, or discrete data). Fortunately, this subject-level approach may be implemented in WinBUGS, a freely available software package that employs Gibbs sampling and several of its variants.³⁸ The computational burden of constructing the conditional distributions and enacting Gibbs sampling (possibly involving ARS) is handled by the program. Using WinBUGS, SEM researchers can estimate their model without great difficulty merely by specifying the model in accordance with the WinBUGS language. 

In the illustrations below, we employ WinBUGS to enact the subject-level parameterization (code for running the model is given in the appendix). WinBUGS offers a variety of distributional forms for specifying prior distributions. To mimic the moment-level data approach illustration done in AMOS, we employ diffuse uniform prior distributions. The prior distributions for the loadings, structural coefficients, and covariances are each U(-10000, 10000). The prior distributions for each variance (i.e., of factors or errors) are each U(0, 100000). Alternative choices for prior distributions include generalized conjugate priors (Press, 1989; Rowe, 2003) using inverse-gamma and inverse-Wishart distributions for variances and covariance matrices and normal distributions for loadings and structural coefficients;⁹ Rowe;⁴⁴ Spiegelhalter et al.,³⁸). Still other parameterizations involve placing uniform or folded-noncentral t prior distributions on standard deviations (Gelman,⁴⁵). Although there are many technical details regarding the implementation of the MCMC algorithm (e.g., initial values, convergence criteria, jump sizes, etc.), the purpose of the current work is to compare the moment-level and subject-level approaches to MCMC estimation in SEM. Note that WinBUGS program does not support the likelihood functions for the moment-data approach, therefore, one can utilize the moment-data approach only in conventional SEM software such as AMOS or Mplus. In the next section, these approaches are compared in the context of real-data examples.

Illustration

As an illustration, this study utilized a publicly available data obtained from the Program for International Student Assessment (PISA) 2003 dataset. PISA is organized by the Organization for Economic Cooperation and Development (OECD), an intergovernmental organization of industrialized countries, and is a system of international assessments, which focus on the capabilities of 15 year-olds within three domains of literacy (mathematical, scientific, and reading) (NCES,⁴⁶). Starting in 2000, PISA has been administered every three years. In 2003, the U.S. had 274 schools and 5,456 students participate.

In this illustration, we use the model depicted in Figure 1, in which we hypothesize the student-teacher relationship factor (STUREL) indicated by the five items (ST26Q01 to ST26Q05) influences the students’ attitudes towards school factor (ATSCHL) indicated by the four items (ST26Q01 to ST26Q05). See Table 1 for more detailed description of these measures. Also, for the purpose of investigating the sample size impact on the computational burdens of both approaches, we analyzed two different sample sizes, the large sample scenario (n = 5, 176; all U.S. student participations with complete data) and the small sample size scenario (n = 100; the first 100 student respondents with complete data). See Table 2 for the summary statistics for both sample size scenarios.

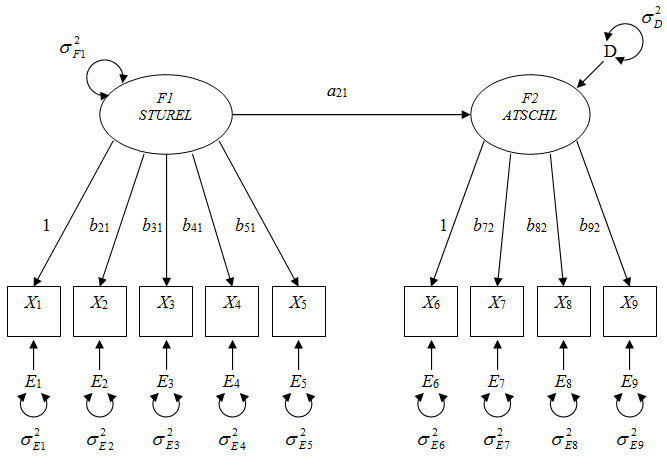
Figure 1 The example SEM diagram. b is loading parameter; F is factor; X is indicator; E is error; ${\sigma }_{}^2$ is variance.

Traditional estimation method results

ML estimation was carried out using AMOS 7.0. The data-model fit for the model with the untransformed data was satisfactory for both small sample size case (e.g., χ2 = 38.195 with df = 26 [p=.058], RMSEA [Root Mean Square Error of Approximation] = .069, CFI [Comparative Fit Index] = .965), and large sample size case (e.g., χ2 = 617.248 with df = 26 [p<.001], RMSEA [Root Mean Square Error of Approximation] = .066, CFI [Comparative Fit Index] = .954). ML parameter estimates for both sample size data are summarized in Tables 3 and 4. 

Moment-level data approach MCMC Rresults

MCMC estimation for Moment-level Data approach was also carried out using AMOS 7.0 using the covariance matrices and means vector in Table 2 for both sample size scenarios. AMOS takes ML estimates as starting values, and we’ve set up 5,000 burn-in and tried 50,000 MCMC run after burn in. i.e., 55,000 total MCMC run. Regarding prior, we adapted diffuse priors for all parameters with the default prior distribution in AMOS 7.0, i.e., uniform from -3.4*10^38 to -3.4*10^38.

MCMC estimates using Moment-level data approach, i.e., the Wishart likelihood function with covariance data, are summarized in Table 3 and Table 4. Marginal densities and trace plots (chain histories) are also provided in Figure 2 and Figure 3. Note that, due to the space issue, the results of three error variances (${\hat{\sigma }}_{E7}^2$,${\hat{\sigma }}_{E8}^2$, and ${\hat{\sigma }}_{E9}^2$) were omitted. This chain history results suggest that convergence was reached. The rapid change in the history indicates the chain is mixing quite well and explores the support of the distribution, as shown in the marginal densities for the parameters. Also, not only the MCMC estimations were performed in relative short periods of time, but also both sample size scenarios yield almost same estimation time as we expected (55,000 MCMC runs in 45 seconds for small sample size and 47 seconds for large sample size using Pentium 4 CPU personal computer). Furthermore, table 3 and Table 4 confirm that estimates based on this MCMC algorithm (again, with diffuse prior) are comparable to those obtained for both sample size cases.

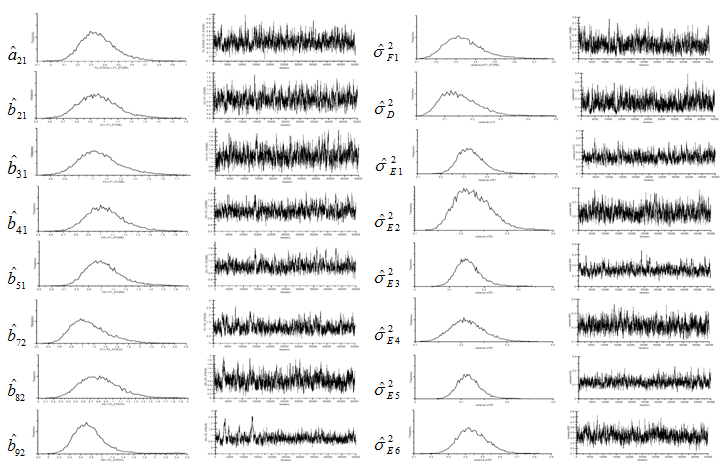
Figure 2 Marginal Densities and Trace Plots of Moment-level Data Approach for Small Sample (n=100) Example.

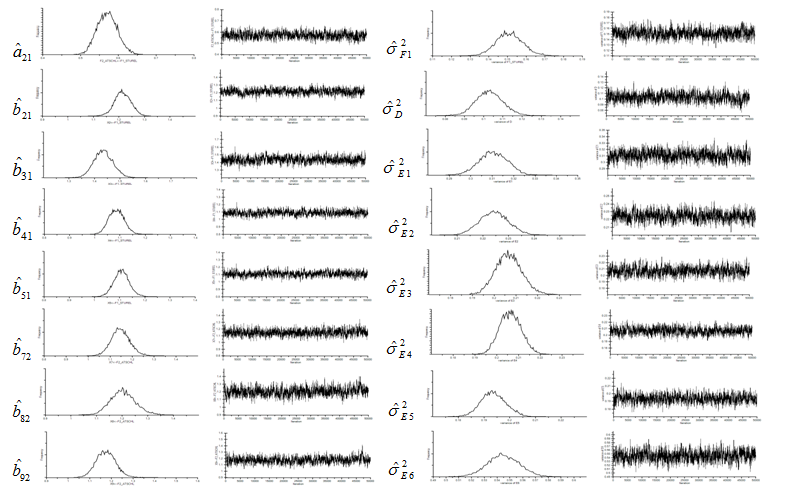
Figure 3 Marginal Densities and Trace Plots of Moment-level Data Approach for Large Sample (n=5,176) Example.

Subject-level data approach MCMC results

The results of the MCMC estimation using the subject-level data approach are summarized in Table 3 and Table 4. Marginal densities and trace plots (not shown on space considerations; available from the authors upon request) were comparable to those from the moment-level approach, indicating convergence, adequate mixing, and sampling throughout the support of the distribution. The estimation in WinBUGS took 122 seconds with the small sample and 13,187 seconds (3 hours and 40 minutes) with the large sample. As is evident from Tables 3 and 4, the posterior distributions (as summarized by their means, medians, standard deviations, and 95% credibility intervals) in the moment- and subject-level data approaches are nearly identical to each other. Owing to the use of diffuse prior distributions, the posterior means and medians are close to the ML estimates.

The principal difference between the moment- and subject-level data approaches was the time taken to conduct the estimation. For the moment-level approach, the computational time was comparable for the two sample sizes. For the subject-level approach, the computational time for the large sample was considerably larger and may prove to be prohibitively large for researchers. The additional computational burden of the subject-level approach is due to the need to draw a value for every latent factor for every subject. This implies that N×M parameters (where M is the number of latent factors) need to be drawn at each iteration of the MCMC process in the subject-level approach above and beyond those required by the moment-level approach.                

MCMC estimation often requires large numbers of iterations (Gilks, et al.,¹⁴), necessitating efficient computational strategies. As this example shows, considerable differences (by a factor of 293 for large sample case) between computational speeds may be observed between a subject-level data and moment-level data approach. Therefore, we can easily expect that the full-information MCMC approach quickly becomes infeasible or impractical as sample size increases. This was evident in the current, relatively simple example of a model with two latent factors and nine observables. Similarly, the difference in the computational burdens would likely be larger in the context of models with more latent variables. This may be exacerbated by more complex models which may require more iterations for convergence and/or mix more slowly, necessitating more iterations after convergence to adequately represent the posterior. In such cases, the computational simplicity of the moment-level approach may offer even greater efficiencies in estimation.^47-57 

Markov chain Monte Carlo (MCMC) estimation method is increasingly popular in a variety of latent variable models such as SEM. In the SEM framework, one can apply different MCMC approaches according to different types of data. In this paper, two major MCMC approaches (i.e., the moment-level data approach and the subject-level data approach) were compared using two a two-factor model with a directional path on real data sets. Firstly, this paper illustrated the two major SEM MCMC approaches (i.e., the moment-level data approach and the subject-level data approach). Then, we showed how the moment-level MCMC method reduces computational loads and simplifies the MCMC process as compared to the subject-level approach. Specifically, in this paper example we saw considerable differences (by a factor of 293 for large sample case) between computational speeds between a subject-level data and moment-level data approach. Given the fact that MCMC estimation often requires large numbers of iterations (Gilks, et al.,¹⁴), efficient computational strategies are much needed in practice. Moreover, the difference in the computational burdens would likely be larger in the context of models with more latent variables. In such cases, the computational simplicity of the moment-level approach may offer even much greater efficiencies in estimation, and these computational advantages of the moment-level data approach over the subject-level data approach are much appreciated and desirable.

In sum, the current paper makes three contributions to the emerging SEM literature on MCMC estimation. First, recently the most enlightened estimation method in SEM, MCMC estimation methods were compared not only methodological view, but also practical point of view. Second, it is illustrated that the methodological feasibility of MCMC estimation in SEM can be secured by the moment-level data MCMC approach using real-datasets. This is especially relevant in situations in which the data set is large or when only summary information is available. Third, because the Wishart distribution function (similar to the well-known ML function) was used, this the moment-level data MCMC approach can simplify the MCMC process and provide a more intuitive understanding of MCMC estimation process to SEM users. Finally, this research may lead to a natural way to implement or improve MCMC estimation into conventional SEM software. 

All analysis in this paper are based on diffuse prior case. As mentioned before, MCMC also allows us to explicitly investigate the sensitivity of prior distributions for parameters when used in the context of Bayesian inference. The capability of cooperating prior into the estimation procedure would be a distinctive advantage of Bayesian approach over the traditional approaches. Investigating the appropriate use and/or advantages of using prior in the context of SEM is unanswered and remains as future study.

Finally, our elaboration this paper has only focused on the metrical indicator case (observed data is ratio or interval) which requires normality assumption. Given popularity of ordinal data in social and behavioral research, comparing and providing practical/mythological guideline on MCMC estimation methods with such data would greatly help researchers who are interested in analyzing such data with SEM models.

None.

Author declares that there are no conflicts of interest.

1. Bollen KA. Structural equation modeling with latent variables. Wiley, New York, USA. 1989.
2. Browne MW. Generalized least-squares estimators in the analysis of covariance structures. South African Statistical Journal. 1974;8(1):1–24.
3. Browne MW. Asymptotically distribution-free methods for the analysis of covariance structures. British Journal of Mathematical and Statistical Psychology. 1984;37(1):62–83.
4. Lee SY. Structural equation modeling: a bayesian approach. USA: West Sussex, John Wiley & Sons Ltd; 2007:458.
5. Süli E, Mayers D. An Introduction to Numerical Analysis. India: Cambridge University Press; 2003:429.
6. Andrieu C, Freitas N, De Doucet NA, et al. An introduction to MCMC for machine learning. Machine Learning. 2003;50:5–43.
7. Dyer M, Frieze A, Kannan R. A random polynomial-time algorithm for approximating the volume of convex bodies. Journal Association Computing Machines. 1991;38(1):1–17.
8. Jerrum M, Sinclair A. The Markov chain Monte Carlo method: an approach to approximate counting and integration. Approximation algorithms for NP-hard problems In: DS Hochbaum, et al. ed. Bostan, PWS Publishing; 1996:482–520.
9. Arminger G, Muthén BO. A Bayesian approach to nonlinear latent variable models using the Gibbs sampler and the Metropolis-Hastings algorithm. Psychometrika. 1998;63(3):271–300.
10. Lee SY, Song XY. Model comparison of nonlinear structural equation models with fixed covariates. Psychometrika. 2003;68(1):27–47.
11. Scheines R, Hoijtink H, Boomsma A. Bayesian estimation and testing of structural equation models. Psychometrika. 1999;64(1):37–52.
12. Song XY, Lee SY. Bayesian estimation and test for factor analysis model with continuous and polytomous data in several populations. British Journal of Mathematical and Statistical Psychology. 2001;54(2): 237–263.
13. Song XY, Lee SY. A Bayesian approach for multigroup nonlinear factor analysis. Structural Equation Modeling: A Multidisciplinary Journal. 2002;9(2):523–553.
14. Gilks WR, Richardson S, Spiegelhalter DJ. Markov chain Monte Carlo in practice. New York, USA: Chapman and Hall; 1996:504.
15. Levy R, Choi J. An introduction to Bayesian Structural Equation Modeling. In: Hancock GR, Mueller RO. Structural equation modeling: a second course. 2nd ed. CT: Information Age Publishing, Inc. 2013.
16. Chen J, Choi J, Stapleton L, et al. An empirical evaluation of mediation effect analysis with manifest and latent variables using markov chain monte carlo and alternative estimation methods. Structural Equation Modeling: A Multidisciplinary Journal. 2014;21(2):253–262.
17. Choi J, Dunlop M, Chen J, et al. A comparison of different approaches for coefficient alpha for ordinal data. Journal of Educational Evaluation. 2011;24(2):485–506.
18. Choi J, Kim S, Chen J, et al. A Comparison of Maximum Likelihood and Bayesian Estimation for Polychoric Correlation using Monte Carlo Simulation. Journal of Educational and Behavioral Statistics. 2011;36(4):523–549.
19. Shi JQ, Lee SY. Bayesian sampling-based approach for factor analysis models with continuous and polytomous data. British Journal of Mathematical and Statistical Psychology. 1998;51(2):233–252.
20. Lee SY, Song XY. Evaluation of the Bayesian and maximum likelihood approaches in analyzing structural equation models with small sample sizes. Multivariate Behavioral Research. 2004;39(4):653–686.
21. Levy R, Mislevy RJ. Bayesian Psychometric Modeling. USA, FL: Chapman & Hall/CRC; 2016:466.
22. Levy R, Mislevy RJ, Behrens JT. Markov chain Monte Carlo in educational research. In: Gelman A, et al. ed. Handbook of Markov chain Monte Carlo: Methods and applications. 2010.
23. Metropolis N, Ulam S. The Monte Carlo method. Journal of American Statistical Association 1949;44(247):335–341.
24. Metropolis N, Rosenbluth A, Rosenbluth R, et al. Equation of state calculations by fast computing machines. Journal of Chemical Physics. 1953;21:1087–1091.
25. Jeffreys Sir H. Theory of Probability. New York, USA: Oxford University Press; 1961:470.
26. Edwards AWF. Likelihood (Expanded Edition). USA: Johns Hopkins University Press; 1992:296.
27. Hastings WK. Monte Carlo sampling methods using Markov chains and their applications. Biometrika. 1970;57(1):97–109.
28. Lynch SM. Introduction to applied Bayesian statistics and estimation for social scientists. New York: Springer; 2007;359.
29. Tierney L. Markov chains for exploring posterior distributions. Ann Statist. 1994;22(4):1701–1728.
30. Choi J. Estimating Structural Equation Models within a Bayesian Framework: A Concrete Example of a Markov chain Monte Carlo Method. 2017.
31. Choi AN, Lee MS, Cheong KJ, et al. Effects of group music intervention on behavioral and psychological symptoms in patients with dementia: a pilot-controlled trial. Int J Neurosci. 2009;119(4):471–481.
32. Levy R. Posterior predictive model checking for multidimensionality in item response theory and Bayesian networks. USA: University of Maryland; 2006:1–219.
33. Arbuckle JL. Amos 7.0 User’s Guide. SPSS Inc, Chicago, Illinois, USA, 2006:1–583.
34. Gelfand AE, Smith AFM. Sampling-based approaches to calculating marginal densities. Journal of the American Statistical Association. 1990;85(410):398–409.
35. Geman S, Geman D. Stochastic relaxation, Gibbs distribution and Bayesian restoration of images. IEE Transactions on Pattern Analysis and Machine Intelligence. 1984;6(6):721–741.
36. Ripley B. Stochastic Simulation. New York: Wiley; 1987:237.
37. Gilks WR. Derivative-free adaptive rejection sampling for Gibbs sampling. In: Bernardo J, et al. ed. Oxford University Press; 1992.
38. Spiegelhalter DJ, Thomas A, Best NG, et al. WinBUGS version 1.4: user manual. Cambridge Medical Research Council Biostatistics Unit, UK, 2003:1–60.
39. Mardia KV, Kent JT, Bibby JM. Multivariate Analysis. 1st ed. USA: Academic Press; 1979:521.
40. Browne MW. Robustness of statistical inference in factor analysis and related models. Biometrika. 1987;74:375–384.
41. Yuan KH, Bentler PM. Normal theory based test statistics in structural equation modelling. British Journal of Mathematical and Statistical Psychology. 1998;51(2):289–309.
42. Lee SY, Song XY. Bayesian model selection for mixtures of structural equation models with an unknown number of components. British Journal of Mathematical and Statistical Psychology. 2003;56(1):145–165.
43. Lee SY, Zhu HT. Statistical analysis of nonlinear structural equation models with continuous and polytomous data. British Journal of Mathematical and Statistical Psychology. 2000;53:209–232.
44. Rowe DB (2003) Multivariate Bayesian statistics: Models for source separation and signal unmixing. USA: CRC Press; 2003.
45. Gelman A. Prior distributions for variance parameters in hierarchical models. Bayesian Analysis. 2006;1:515–534.  
46. NCES. Program for international student assessment (PISA). 2008.
47. Gelman A. Inference and monitoring convergence. In: Gilks WR, et al. editors. Markov Chain Monte Carlo in Practice, London: Chapman and Hall; 1996:131-143.
48. Gelman A, Carlin JB, Stern HS, et al. Bayesian data analysis. London: Chapman & Hall, USA, 1995:690.
49. Gill J. Bayesian Methods: A Social and Behavioral Sciences Approach. FL: Chapman & Hall/CRC, USA, 2002:724.
50. Gilks WR, Best NG, Tan KKC. Adaptive rejection Metropolis sampling. Applied Statistics. 1995;44:455–472.
51. Gilks WR, Wild P. Adaptive rejection sampling for Gibbs sampling. Applied Statistics. 1992;41:37–348.
52. Jöreskog K. A general approach to confirmatory maximum likelihood factor analysis. Psychometrika. 1969;34(2):183–202.
53. Muthén LK, Muthén BO. Mplus user’s guide. 3rd ed. Muthén & Muthén, CA, USA. 2004.
54. Press SJ. Bayesian statistics: Principles, models and applications. Wiley, New York; 1989:256.
55. Roberts GO, Gelman A, Gilks WR. Weak convergence and optimal scaling of random walk metropolis algorithms. Annals of Applied Probability. 1997;7(1):110–120.
56. Roberts GO, Rosenthal JS. Optimal scaling of discrete approximations to langevin difusions. Journal of Royal Statistical Society Series B: Statistical Methodology. 1998;60(1):255–268.
57. The MathWorks. Matlab (Version 6.1). Natick, MA. 2003.