The modeling and analysis of lifetime data are becoming a challenge for the statistician and policy makers because the lifetime data are in general stochastic in nature. During recent decades several one parameter lifetime distributions have been proposed by researchers but they are not suitable due to the nature of the distribution and the stochastic nature of the data. In this paper an attempt has been made to propose a new one parameter lifetime distribution named Komal distribution. The statistical properties, estimation of parameter and application of the distribution to a lifetime dataset have been presented.

Keywords: lifetime distributions, statistical properties, estimation of parameter, applications

In the present era, modeling of lifetime data is a serious challenge because the lifetime data are stochastic in nature. It has been observed that policy makers are struggling to find a suitable distribution for lifetime data. During recent decades several one parameter lifetime distributions have been proposed in Statistics literature but due to distributional nature or the nature of the lifetime data, these proposed distributions do not give proper fit. Several researchers in the field of distribution theory are trying to propose a new lifetime distribution as per the stochastic nature of lifetime data. Upto 1958, there was only one lifetime distribution named exponential distribution which was in use for the analysis and modeling of lifetime data. Lindley¹ proposed another lifetime distribution known as Lindley distribution and Ghitanty et al.² after detailed study on its statistical properties and application observed that Lindley distribution gives much closure fit than exponential distribution. While working on the comparative study of exponential and Lindley distribution, Shanker et al.³ observed that exponential and Lindley distributions are competing well and there were some datasets where these two distributions do not provide good fit. Shanker^4,5 proposed two new one parameter lifetime distributions namely Shanker distribution and Akash distribution which gave much better fit than both exponential and Lindley distribution. Shanker et al.⁶ provides a comparative study on applications of exponential, Lindley and Akash distribution. Further, Shanker & Hagos⁷ presented a detailed study on applications of exponential, Lindley, Shanker and Akash distribution and showed that still there are some datasets where these distributions did not provide better fit. Further, Shanker⁸ introduced Sujatha distribution which provides much better fit than exponential, Lindley, Shanker and Akash distribution. Again, Shanker⁹ proposed another one parameter lifetime distribution named Garima distribution to model data arising from behavioral sciences, but this also does not give good fit on several real lifetime datasets. Now the question is to search a distribution which is both flexible and tractable in nature to capture the variation in the datasets. When a distribution does not give good fit, then some researchers prefer to transform the dataset to satisfy the assumptions of the distribution but this is not a preferable method because the original nature of the dataset gets lost. Some researchers also prefer to modify the distribution by adding extra shape parameter or scale parameter distribution to suit the nature of the dataset. But, instead of transforming the original dataset or modifying the distribution suiting to dataset, it is better to search a new distribution which provides better fit for the given datasets when the existing distributions fails to provide good fit.

In the present paper an attempt has been made to propose a new one parameter lifetime distribution, named Komal distribution, which would provide a better fit over exponential, Lindley, Shanker, Akash and Sujatha distributions. Some of its statistical properties, estimation techniques of parameter and an application to a real lifetime dataset has been discussed and presented.

Taking the convex combination of exponential $\left(\theta \right)$  and gamma $\left(2,\theta \right)$  distributions with respective mixing proportions $\frac{\theta \left(\theta +1\right)}{{\theta }^2+\theta +1}$  and $\frac{1}{{\theta }^2+\theta +1}$ , a new probability density function (pdf) can be expressed as

$f\left(x;\theta \right)=\frac{{\theta }^2}{{\theta }^2+\theta +1}\left(1+\theta +x\right)e^{-\theta x};x>0,\theta >0$

We would call this new distribution as ‘Komal distribution’. Like other one parameter lifetime distributions, Komal distribution has been derived as a convex combination of exponential distribution and gamma distribution, it is expected to give better fit over exponential and other one parameter distributions derived using convex combinations of exponential distribution and gamma distribution. The cumulative distribution function (cdf) of Komal distribution can thus be obtained as

$F\left(x;\theta \right)=1-\left[1+\frac{\theta x}{{\theta }^2+\theta +1}\right]e^{-\theta x};x>0,\theta >0$

The behaviour of the pdf and the cdf of Komal distribution for varying values of parameter $\theta$  have been presented in Figures 1 & 2 respectively.

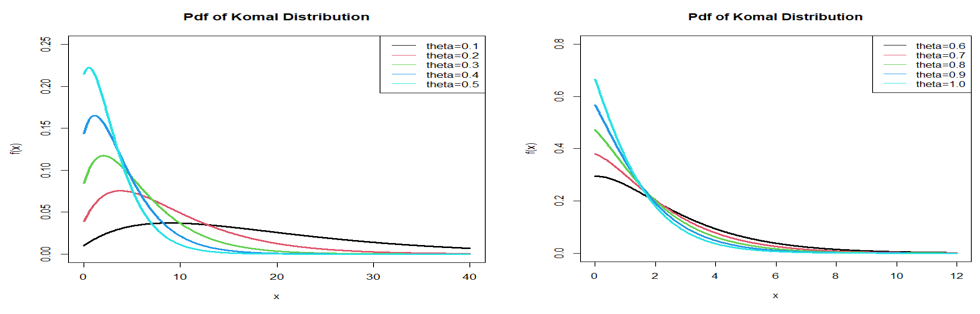
Figure 1 Graphs of the pdf of Komal distribution for selected values of the parameter.

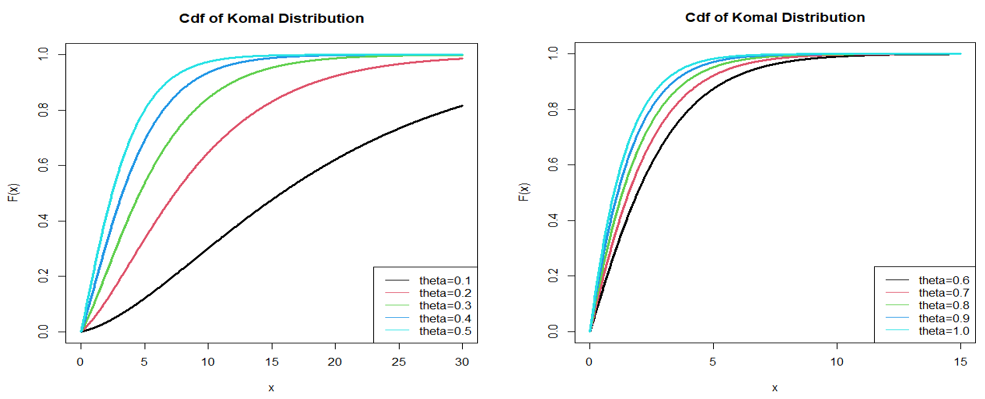
Figure 2 Graphs of the cdf of Komal distribution for selected values of the parameter.

As we know that moments are essential to know the descriptive nature such as coefficient of variation, skewness, kurtosis and index of dispersion of any distribution. Following the approach of obtaining the $r$ th moment of Shanker distribution and Akash distribution by Shanker^4,5, the $r$ th moment about origin ${\mu }_r{}^{\prime }$ of Komal distribution can be obtained as

${\mu }_r{}^{\prime }=E\left(X^r\right)=\frac{{\theta }^2}{{\theta }^2+\theta +1}{\displaystyle \underset{0}{\overset{\infty }{\int }}{x}^r\left(1+\theta +x\right)}{e}^{-\theta x}dx$  

$=\frac{r!\left({\theta }^2+\theta +r+1\right)}{{\theta }^r\left({\theta }^2+\theta +1\right)};r=1,2,3,\cdot \cdot \cdot$   (3.1)

Substituting $r=1,2,3,4$ in (3.1), the first four moments about origin of Komal distribution can be obtained as

${\mu }_1{}^{\prime }=\frac{{\theta }^2+\theta +2}{\theta \left({\theta }^2+\theta +1\right)}$  ,${\mu }_2{}^{\prime }=\frac{2\left({\theta }^2+\theta +3\right)}{{\theta }^2\left({\theta }^2+\theta +1\right)}$

${\mu }_3{}^{\prime }=\frac{6\left({\theta }^2+\theta +4\right)}{{\theta }^3\left({\theta }^2+\theta +1\right)}$  ,${\mu }_4{}^{\prime }=\frac{24\left({\theta }^2+\theta +5\right)}{{\theta }^4\left({\theta }^2+\theta +1\right)}$ .

The moments about the mean of Komal distribution, using relationship between moments about the mean and the moments about the origin, can thus be obtained as

${\mu }_2=\frac{{\theta }^4+2{\theta }^3+5{\theta }^2+4\theta +2}{{\theta }^2{\left({\theta }^2+\theta +1\right)}^2}$   

${\mu }_3=\frac{2\left({\theta }^6+3{\theta }^5+9{\theta }^4+13{\theta }^3+12{\theta }^2+6\theta +2\right)}{{\theta }^3{\left({\theta }^2+\theta +1\right)}^3}$  

${\mu }_4=\frac{3\left(3{\theta }^8+12{\theta }^7+42{\theta }^6+84{\theta }^5+119{\theta }^4+112{\theta }^3+76{\theta }^2+32\theta +8\right)}{{\theta }^4{\left({\theta }^2+\theta +1\right)}^4}$ .

The descriptive constants including coefficient of variation (CV), coefficient of skewness (CS), coefficient of kurtosis (CK) and the index of dispersion (ID) of Komal distribution are thus obtained as

$CV=\frac{\sqrt{{\mu }_2}}{{\mu }_1{}^{\prime }}=\frac{\sqrt{{\theta }^4+2{\theta }^3+5{\theta }^2+4\theta +2}}{{\theta }^2+\theta +2}$  

$CS=\frac{{\mu }_3{}^2}{{\mu }_2{}^3}=\frac{4{\left({\theta }^6+3{\theta }^5+9{\theta }^4+13{\theta }^3+12{\theta }^2+6\theta +2\right)}^2}{{\left({\theta }^4+2{\theta }^3+5{\theta }^2+4\theta +2\right)}^3}$  

$CK=\frac{{\mu }_4}{{\mu }_2{}^2}=\frac{3\left(3{\theta }^8+12{\theta }^7+42{\theta }^6+84{\theta }^5+119{\theta }^4+112{\theta }^3+76{\theta }^2+32\theta +8\right)}{{\left({\theta }^4+2{\theta }^3+5{\theta }^2+4\theta +2\right)}^2}$  

  $ID=\frac{{\mu }_2}{{\mu }_1{}^{\prime }}=\frac{{\theta }^4+2{\theta }^3+5{\theta }^2+4\theta +2}{\theta \left({\theta }^2+\theta +1\right)\left({\theta }^2+\theta +2\right)}$ .

Behaviour of coefficient of variation (CV), coefficient of skewness (CS), coefficient of kurtosis (CK) and index of dispersion (ID) of Komal distribution for changing values of parameter are shown in the Figure 3. The coefficient of variation and the coefficient of skewness are non-decreasing whereas the coefficient of kurtosis and the index of dispersion are non-increasing.

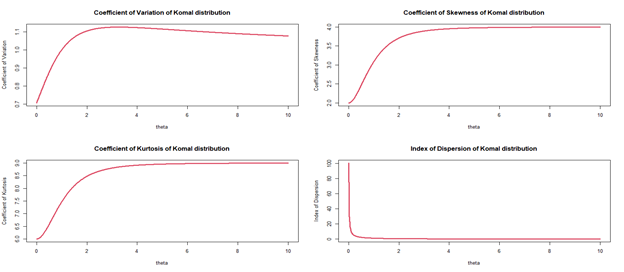
Figure 3 Graph of CV, CS, CK and ID of Komal distribution for values of the parameter.

Hazard rate function

The hazard rate function of a random variable $X$ having pdf $f\left(x;\theta \right)$ and cdf $F\left(x;\theta \right)$ is defined as

$h\left(x,\theta \right)=\underset{\Delta x\to 0}{\lim }\frac{P\left(X<x+\Delta x|X>x\right)}{\Delta x}=\frac{f\left(x;\theta \right)}{1-F\left(x;\theta \right)}$  

Thus, the hazard rate function of Komal distribution can be obtained as

 $h\left(x,\theta \right)=\frac{{\theta }^2\left(1+\theta +x\right)}{\left({\theta }^2+\theta +1+\theta x\right)}$ .

This gives $h\left(0,\theta \right)=\frac{{\theta }^2\left(\theta +1\right)}{{\theta }^2+\theta +1}=f\left(0,\theta \right)$ . The behaviour of the hazard rate function of Komal distribution for various values of parameter $\theta$ is shown in the following Figure 4. The hazard rate of Komal distribution is monotonically non-decreasing. Further, as the values of parameter increases, the hazard rate of Komal distribution scaled up.

Figure 4 Graphs of the hazarad rate function of Komal distribution for selected values of the parameter.

Mean residual life function

Let $X$ be a random variable over the support $\left(0,\infty \right)$  representing the lifetime of a system. Mean Residual life (MRL) function measures the expected value of the remaining lifetime of the system, provided it has survived up to time $x$ . Let us consider the conditional random variable $X_x=\left(X-x|X>x\right);x>0$ . Then, the MRL function, denoted by $m\left(x\right)$ , is defined as

$m\left(x\right)=E\left(X_x\right)=\frac{1}{S\left(x\right)}{\displaystyle \underset{x}{\overset{\infty }{\int }}\left[1-F\left(t\right)\right]}dt$

The MRL function of Komal distribution can thus be obtained as

$m\left(x\right)=\frac{1}{\left\{{\theta }^2+\theta +1+\theta x\right\}{e}^{-\theta x}}{\displaystyle \underset{x}{\overset{\infty }{\int }}t\left({\theta }^2\left(1+\theta +t\right)\right)}{e}^{-\theta t}dt-x$   $=\frac{{\theta }^2+\theta +2+\theta x}{\theta \left({\theta }^2+\theta +1+\theta x\right)}$ .

This gives $m\left(0\right)=\frac{{\theta }^2+\theta +2}{\theta \left({\theta }^2+\theta +1\right)}={\mu }_1{}^{\prime }$ . The behaviour of the mean residual life function of Komal distribution for various values of parameter is shown in the following Figure 5. It is clear that the mean residual life function of Komal distribution is monotonically non-increasing.

Figure 5 Graphs of the mean residual life function of Komal distribution for values of parameter.

Stochastic ordering

In Probability theory and statistics, a stochastic order quantifies the concept of one random variable being bigger than another. A random variable $X$  is said to be smaller than a random variable $Y$  in the

1. Stochastic order $\left(X{\le }_{st}Y\right)$ if $F_X\left(x\right)\ge F_Y\left(y\right)$  for all $x$
2. Hazard rate order $\left(X{\le }_{hr}Y\right)$ if $h_X\left(x\right)\ge h_Y\left(y\right)$  for all $x$
3. Mean residual life order $\left(X{\le }_{mrl}Y\right)$ if $m_X\left(x\right)\ge m_Y\left(y\right)$  for all $x$  
4. Likelihood ratio order $\left(X{\le }_{lr}Y\right)$ if $\frac{f_X\left(x\right)}{f_Y\left(y\right)}$  decrease in $x$

The following results due to Shaked & Shantikumar¹⁰ are well known for establishing stochastic ordering of distributions

Theorem: Let $X~$  Komal distribution $\left({\theta }_1\right)$  and $Y~$  Komal $\left({\theta }_2\right)$ . If  ${\theta }_1>{\theta }_2$, then $X{<}_{lr}Y$  hence $X{<}_{hr}Y$ , $X{<}_{mrl}Y$  and $X{<}_{st}Y$ .

Proof: We have

$\frac{f_X\left(x;{\theta }_1\right)}{f_Y\left(x;{\theta }_2\right)}=\left[\frac{{\theta }_1{}^2\left({\theta }_2{}^2+{\theta }_2+1\right)}{{\theta }_2{}^2\left({\theta }_1{}^2+{\theta }_1+1\right)}\right]\left(\frac{1+{\theta }_1+x}{1+{\theta }_2+x}\right)e^{-\left({\theta }_1-{\theta }_2\right)x}$ .

This gives

$\log \left[\frac{f_X\left(x;{\theta }_1\right)}{f_Y\left(x;{\theta }_2\right)}\right]=\log \left[\frac{{\theta }_1{}^2\left({\theta }_2{}^2+{\theta }_2+1\right)}{{\theta }_2{}^2\left({\theta }_1{}^2+{\theta }_1+1\right)}\right]+\log \left(\frac{1+{\theta }_1+x}{1+{\theta }_2+x}\right)-({\theta }_1-{\theta }_2)x$  

Therefore, $\frac{d}{dx}\log \left[\frac{f_X\left(x;{\theta }_1\right)}{f_Y\left(x;{\theta }_2\right)}\right]=\frac{{\theta }_2-{\theta }_1}{\left(1+{\theta }_1+x\right)\left(1+{\theta }_2+x\right)}-({\theta }_1-{\theta }_2)$

Thus, for ${\theta }_1>{\theta }_2$ , $\frac{d}{dx}\log \left[\frac{f_X\left(x;{\theta }_1\right)}{f_Y\left(x;{\theta }_2\right)}\right]<0$ . this means that $X{<}_{lr}Y$  hence $X{<}_{hr}Y$ , $X{<}_{mrl}Y$  and $X{<}_{st}Y$ .

Method of moment estimate

 Since Komal distribution has one parameter, equating the population mean to the corresponding sample mean $\left(\overline{x}\right)$ , we get the third-degree polynomial equation of parameter $\theta$  in the form

$\overline{x}{\theta }^3+\left(\overline{x}-1\right){\theta }^2+\left(\overline{x}-1\right)\theta -2=0$   .

Solving this third-degree polynomial equation using Newton-Raphson method, we can easily get the moment estimate of the parameter.

Maximum likelihood estimate

Suppose $\left(x_1,x_2,x_3,\mathrm{...},x_n\right)$  be a random sample of size $n$  from Komal distribution. The log likelihood function, $\log L$  of Komal distribution is given by

$\log L={\displaystyle \sum _{i=1}^n\log f\left(x_i;\theta \right)}=n\left\{2\log \theta -\log \left({\theta }^2+\theta +1\right)\right\}+{\displaystyle \sum _{i=1}^n\log \left(1+\theta +x_i\right)-n\theta \overline{x}}$  

The maximum likelihood estimate (MLE) $\left(\widehat{\theta }\right)$  of the parameters $\left(\theta \right)$  of Komal distribution is the solution of the following log likelihood equation

$\frac{d\log L}{d\theta }=\frac{2n}{\theta }-\frac{n\left(2\theta +1\right)}{{\theta }^2+\theta +1}+{\displaystyle \sum _{i=1}^n\frac{1}{1+\theta +x_i}}-n\overline{x}=0$  

This gives

  ${\displaystyle \sum _{i=1}^n\frac{1}{1+\theta +x_i}}+\frac{n\left(\theta +2\right)}{\theta \left({\theta }^2+\theta +1\right)}-n\overline{x}=0$ .

This is a non-linear equation in $\theta$ . This can be solved using Newton-Raphson method available in R software to get the maximum likelihood estimate (MLE) of the parameter $\theta$  by taking the moment estimate of the parameter as the initial value. It should be noted that the method of moment estimate of the parameter will not be the same as that of the MLE.

The application and the goodness of fit of Komal distribution has been discussed with a failure time dataset. Following failure time dataset has been considered.

Data set: The following skewed to right dataset relating to the failure times of 20 electric bulbs discussed by Murthy et al.¹¹ is considered and the observations are:

1.32, 12.37, 6.56, 5.05, 11.58, 10.56, 21.82, 3.60, 1.33, 12.62, 5.36, 7.71, 3.53, 19.61, 36.63,

0.39, 21.35, 7.22, 12.42, 8.92.

The values ML estimates of parameter and its standard error in parenthesis, $-2\log L$ , AIC (Akaike Information Criterion), AICC (Akaike Information Criterion corrected), BIC (Bayesian Information criterion), K-S (Kolmogorov-Smirnov) for the considered distributions for the given dataset have been computed and presented in table 2. The formulae for computing AIC, AICC, BIC and K-S Statistics are as follows:

  $AIC=-2logL+2k$ , $AICC=AIC+\frac{2k(k+1)}{n-k-1}$ , $BIC=-2logL+k\log n$ , $D=\underset{x}{Sup}|F_n\left(x\right)-F_0\left(x\right)|$  .

$\text{where }k=\text{ number of parameter},n=\text{ sample size}$

The pdf and the cdf of the fitted distributions are given in the Table 1.

The fitted plots of considered distributions for the given datasets have been presented in Figure 6. The goodness of fit in Table 2 and the fitted plots of distributions for the dataset in figure 6 show that Komal distribution provides best fit over exponential, Lindley, Shanker, Akash and Sujatha distributions and therefore Komal distribution can be considered as the most suitable lifetime distribution for modeling lifetime data from biomedical science and engineering.

Figure 6 Fitted plots of distributions considered for dataset.

In this paper a new lifetime distribution named Komal distribution for analysing and modeling lifetime data from biomedical science and engineering has been proposed. Some of its important statistical properties, estimation of parameter and application to a real lifetime dataset from survival analysis has been presented. Since the distribution is new one, it would be of great hope and expectation that this will capture the attention of researchers working in biomedical science, engineering and insurance to model lifetime data in their respective fields. As the distribution has flexibility, tractability and practicability, future of the distribution would be quite bright among researchers in biomedical sciences and engineering.

The author is thankful to the editor in chief of the journal and the anonymous reviewer of the paper for fruitful comments.

The author declares that there are no conflicts of interest.

None.

1. Lindley DV. Fiducial distributions and Bayes’ theorem. Journal of the Royal Statistical Society, Series B. 1958;20(1):102–107.
2. Ghitany, M.E., Atieh, B, Nadarajah S. Lindley distribution and its application, mathematics computing and simulation. 2008;78:493–506.
3. Shanker R, Hagos F, Sujatha S. On modeling of lifetimes data using exponential and Lindley distributions. Biom Biostat Int J. 2015;2(5):140–147.
4. Shanker R. Shanker distribution and its applications. International Journal of Statistics and Applications. 2015a;5(6):338–348.
5. Shanker R. Akash distribution and its applications. International Journal of Probability and Statistics. 2015b;4(3):65–75.
6. Shanker R, Hagos F, Sujatha, S. On modeling of lifetime data using one parameter Akash, Lindley and exponential distributions. Biom Biostat Int J. 2016;3(2):54–62.
7. Shanker R, Hagos F. On modeling of lifetime data using Akash, Shanker, Lindley and exponential distributions. Biom Biostat Int J. 2016;3(6):214–224.
8. Shanker R. Sujatha distribution and its applications. Statistics in Transition-New Series. 2016a;17(3):391–410.
9. Shanker R. Garima distribution and Its application to model behavioral science data. Biom Biostat Int J. 2016b;4(7):275–281.
10. Shaked M, Shanthikumar JG. Stochastic orders and their applications. New York: Academic Press; 1994.
11. Murthy DNP, Xie M, Jiang R. Weibull models. New York: John Wiley & Sons; 2004.