Current joint models for longitudinal and time to event data are not sufficient for longitudinal ordinal outcomes. Three joint models for longitudinal ordinal variables and time to event data were suggested. In each joint model, cumulative logit, or continuation-ratio logit and or cumulative probit mixed effects models for the longitudinal ordinal outcome is associated with the time to event variable by random effects approach. Joint modeling likelihood approach, including ordinal repeated measure sub-model and time to event sub-model were constructed. A SAS macro on importance sampling procedure utilizing adaptive gaussian quadrature and conjugate gradient technique algorithm was used to obtain the maximum likelihood estimates of the parameters. This joint model provides inferences for both the longitudinal ordinal variables and time to event simultaneously. Also, a simulation study on various scenarios (concerning different sample size and different correlations among ordinal longitudinal variables) was conducted. The method was applied to the Tehran Lipid and Glucose Study (TLGS) data. The results in simulation study and real data set supports the applicability of the model.

Keywords: longitudinal data, survival, joint modeling, ordinal

TLGS, tehran lipid and glucose study; CONGRA, conjugate gradient; CLM, cumulative logit mixed effect model

In follow-up studies, both longitudinal and survival data are typically recorded for each sample unit. Since separate longitudinal and survival models are not ideal in this case, by the way the association between these two sets should be considered.¹ In the past, the method was used to calculate this association that today of these methods is known as naïve methods. These methods can be cited Cox and two-stage models.^2,3 Although these methods have advantages such as easy and quick calculation but using these methods the bias caused by measurement error or informative censoring of longitudinal variable cannot completely handled.^4,5

Another way to use it more and more, the use of the class of models called "joint models for longitudinal and survival data " that actually includes the association structure between repeated measures and survival times is repetitive.^6,7 This model was first proposed by Schluchter .⁸ Tsiatis and Davidian reviewed the motivation for and development of joint models; they deal with the structure of the likelihood for model parameters that illuminates the nature of common assumptions, and explain some suggestions for application and inference.⁹ in brief, using joint models, because of the correlation structure between variables it is possible to measure the similarity of the change in the different response variables from the model in addition to, the changes in the levels of one of the variables respond to changes at other levels leads to shall appear.¹⁰ However, most of the investigations are associated with continuous repeated measurements and studies considering the ordinal longitudinal variables are rare.^11-13 In many situations instead of observing continuous outcomes, repeated ordinal outcomes are recorded over time. The joint modeling of ordinal longitudinal outcomes and the time to event data are quite enthusiastic in practice, however, have been less considered since turned out to be a little difficult and necessitates a very different methodology in modeling.^11-14 Since, the data from ordinal level measurements increases the complexity of the likelihood, in this paper a methodology was developed whereby a joint likelihood, based on ordered longitudinal variable and time to event data, is maximized. This model consists of two parts: (I) different type of mixed effects ordinal regression sub-model to ordinal level trajectories which is a proportional odds model for the longitudinal ordinal measurements¹⁵ and (II) a parametric time to event model or survival sub-model.^16,17 The two sub-models were linked via the joint distribution of the random effects in (I) and (II). The longitudinal sub-models used are cumulative logit, continuation-ratio logit and cumulative probit mixed effects models.¹⁵

Also, conjugate gradient (CONGRA) algorithm and importance sampling utilizing gaussian quadrature are used to optimize the joint likelihood function and approximate the integral likelihood function on random effects for jointly estimate the parameters addressed in longitudinal and time to event sub-models simultaneously as well as the association parameter and their precision.^18,19

The rest of the paper is organized as follows: Section 2 describes the model and the likelihood. Section 3 describes computational method description (algorithm and execution). Section 4 describes a simulation study and the protocol. Section 5 describes application of the findings of the study on real data and finally sections 6 and 7 include discussion and concluding remarks on finding of this study.

As noted, this model consists of two parts: (I) The longitudinal sub-models used are cumulative logit, continuation-ratio logit and cumulative probit mixed effects models and (II) a parametric time to event model or survival sub-model.^16,17 The two sub-models were linked via the joint distribution of the random effects in (I) and (II). Assuming that there are N subjects in the study,$Y_i\left(t\right)$ denotes longitudinal ordinal variable in time t for subject $i(i=1.\dots .N)$ with $K$ categories. It is essential to note that in fact, there is no possibility of observing $Y_i\left(t\right)$ at any point in time and these observations are available only in specific time. Thus, longitudinal data observed includes measurements $Y_{ij}=\{Y_i\left(t_{ij}\right) ;j=1.\dots .n_i\}$ and is equal to the values of longitudinal measurements observed over $n_i$ times for subject $i$. The proportional odds version of cumulative logit mixed effect model (CLM) for longitudinal ordinal outcome by conditioning on random component $(U_i~\mathcal{N}\left(0.{\Sigma }_U\right))$ defined as

$\text{logit}\left(P(Y_i\left(t\right)\le k)\right|u;x)=log\left[\frac{P(Y_i\left(t\right)\le k)}{1-P(Y_i\left(t\right)\le k)}|u;x\right]={\alpha }_k-\left[{\beta }^{\text{'}}{X}_i\left(t\right)+{U^{\text{'}}}_i{Z}_i\left(t\right)\right]. (k=1.\dots .K-1)$ (1)

Where $X_i\left(t\right)$ and $Z_i\left(t\right)$ are the design matrix of fixed and random effects; ${\alpha }_{\text{k}}$ and β are category cut points and the vector of regression coefficients, respectively.^15,20 Proportional-odds cumulative logit model is possibly the most popular logistic regression model for ordinal data.²¹

The continuation-ratio logits model(CRM) can be considered as such condition.

$logit\left(P(Y_i\left(t\right)=k\text{|}Y\ge k)\right)=log\left[\frac{P(Y_i\left(t\right)=k\text{|}Y\ge k)}{1-P(Y_i\left(t\right)=k\text{|}Y\ge k)}\right]$
$={\alpha }_k-\left[{\beta }^{\text{'}}{X}_i\left(t\right)+{U^{\text{'}}}_i{Z}_i\left(t\right)\right]. (k=1.\dots .K-1)$                    (2)

This model is applicable in cases where an subject should be present before being placed in category j in a higher category.¹⁵

The cumulative probit model (CPM) also can be written in this position which probit link function is the inverse of the standard normal cdf $\left({\Phi }^{-1}\right)$.

${\Phi }^{-1}\left(P(Y_i\left(t\right)\le k)\right)={\alpha }_k-\left[{\beta }^{\text{'}}{X}_i\left(t\right)+{U^{\text{'}}}_i{Z}_i\left(t\right)\right]. (k=1.\dots .K-1)$                     (3)

In cases where the main emphasis is on models with latent variables, particularly in econometrics; the cumulative probit model is used more than the cumulative logit model.²² For longitudinal sub-model, because of the similarity process, only cumulative logit mixed effect model is expressed in the following manner.

Considering a model (1) that $Y_i\left(t\right)$ are independent and identically distributed as

$\left\{\begin{array}{l}{\pi }_{ik}\left(t\right)=P(Y_i\left(t\right)=k\text{|}u;x)=\frac{exp({\alpha }_k-\left[{\beta }^{\text{'}}{X}_i\left(t\right)+{U^{\text{'}}}_i{Z}_i\left(t\right)\right])}{1+exp({\alpha }_k-\left[{\beta }^{\text{'}}{X}_i\left(t\right)+{U^{\text{'}}}_i{Z}_i\left(t\right)\right])}-\frac{\exp ({\alpha }_{k-1}-\left[{\beta }^{\text{'}}{X}_i\left(t\right)+{U^{\text{'}}}_i{Z}_i\left(t\right)\right])}{1+\exp ({\alpha }_{k-1}-\left[{\beta }^{\text{'}}{X}_i\left(t\right)+{U^{\text{'}}}_i{Z}_i\left(t\right)\right])}\\ m_i\left(t\right)=E(Y_i\left(t\right)\text{|}u;x)=g^{-1}\left[{\beta }^{\text{'}}{X}_i\left(t\right)+{U^{\text{'}}}_i{Z}_i\left(t\right)\right]\\ \\ U_i~\mathcal{N}\left(0.{\Sigma }_U\right)\left(4\right)\end{array}\right\}$

Where $m_i\left(t\right)$ is unobserved real value of longitudinal measurement at time t and $g(.)$ is monotonic link function. Because the value of $Y_i\left(t\right)$ contains the measurement error, then, $m_i\left(t\right)$ is different from $y_{\text{i}}\left(\text{t}\right)$.

We assume are lative risk regression sub-model for the time to event data. Then the time to event sub-modelis as follows:

$\begin{array}{l}{h}_i(t\text{|}{\mathcal{M}}_i\left(t\right).w_i)=\underset{dt\to 0}{\lim }Pr\{t\le T_i^{*}⟨t+dt|T_i^{*}\ge t.{\mathcal{M}}_i\left(t\right).w_i\}/dt \\ =h_o\left(t\right)exp\{w_i+\alpha m_i\left(t\right)\}. t>0\end{array}$                           (5)

Where $T_{\text{i}}^{\text{*}}$ in is real survival time, ${\mathcal{M}}_i\left(t\right)=\{m_i\left(s\right).0\le s<t\}$ is the history of unobserved real value of longitudinal measurement up to time t, $h_o\left(t\right)$ is the baseline hazard function, ${\omega }_{\iota }$is the vector of covariates corresponding to regression coefficients of γ, and finally the α is the association parameter for the expectation of the longitudinal endpoint and survival. Hence with this formulation, one assumes that the risk of an event at time t is dependent on the true value of the longitudinal outcome at that time.⁶ However, this assumption is unacceptable for survival function. Because in the terms of survival function, the model is as follow which will be incorporated in the joint model:

$S_i(t\text{|}{\mathcal{M}}_i\left(t\right).w_i)= Pr\left\{T_i^{*}>t|{\mathcal{M}}_i\left(t\right).w_i\right\}$
$=exp\left(\underset{0}{\overset{t}{{\displaystyle \int }}}{h}_0\left(s\right)exp\left\{\stackrel{\text{'}}{\gamma }+\alpha m_i\left(s\right)\right\}ds\right)$               (6)

Among the methods to estimate the parameters in a joint model (23-28), the most popular is the method of maximum Likelihood.^29,30 According this method, to combine the two sub-models of (I) and (II), the distribution of observed outcomes of $\{T_i.{\delta }_i.y_i\}$ is required where ${\delta }_i$ denotes the event indicator andadditionally, the time independent vector of random component $u_i$. This component covers the association between the longitudinal and time to event sub-models as well as the relationship among the longitudinal measurements.

$p(T_i.{\delta }_i.y_i\text{|}{u}_i;\theta )=p\left((T_i.{\delta }_i\text{|}{u}_i;\theta )p\left(y_i\right|u_i;\theta \right)$                     (6)

$p(y_i\text{|}{u}_i;\theta )=\prod _{j}p\left(y_i\left(t_{ij}\right)|u_i;\theta \right)$                     (7)

Where $\theta ={({\theta }_t^T.{\theta }_y^T.{\theta }_u^T)}^T$ is the vector of parameters in time to event and longitudinal and random effects and $y_i$ is the $n_{\text{i}}\times 1$ dimensional vector of longitudinal measurements for i-th subject in the study. Assuming that the missing mechanism and visiting process are independent of real time to event and future longitudinal measurements, the i-th subject contributes the log likelihood as follow:

$logp(T_i.{\delta }_i.y_i\text{|}{u}_i;\theta )=log{\int }^{\text{}}p(T_i.{\delta }_i.y_i\text{|}{u}_i;\theta )d{u}_i$                       (8)

$=log{\int }^{\text{}}p(T_i.{\delta }_i\text{|}{u}_i;{\theta }_t.\beta )\left[\prod _{j}p\left(y_i\left(t_{ij}\right)\right|u_i;{\theta }_y)\right]p(u_i;{\theta }_u)d{u}_i$

or

$\begin{array}{l}\text{logp}\left({{\rm T}}_{\text{i}}.{\delta }_{\text{i}}.{\text{y}}_{\text{i}}|{\upsilon }_{\text{i}};\theta \right)\\ =log\int \prod _{t=1}^{n_i}\prod _{k=1}^k(\frac{exp({\alpha }_k-\left[{\beta }^{\text{'}}{X}_i\left(t\right)+{U^{\text{'}}}_i{Z}_i\left(t\right)\right])}{1+exp({\alpha }_k-\left[{\beta }^{\text{'}}{X}_i\left(t\right)+{U^{\text{'}}}_i{Z}_i\left(t\right)\right])}\\ {\frac{-exp({\alpha }_{k-1}-\left[{\beta }^{\text{'}}{X}_i\left(t\right)+{U^{\text{'}}}_i{Z}_i\left(t\right)\right])}{1+exp({\alpha }_k-\left[{\beta }^{\text{'}}{X}_i\left(t\right)+{U^{\text{'}}}_i{Z}_i\left(t\right)\right])})}^{d_{ikt}}\\ \times {\left(2\pi \right)}^{-\frac{q_u}{2}}det{\left(D\right)}^{-\frac{1}{2}}exp(-D^{-1}{u}_i/2)\}\\ \times {\left[h_o\left(T_i\right)exp\{w_i+\alpha m_i\left(T_i\right)\}\right]}^{{\delta }_i}\\ \times exp\left(\underset{0}{\overset{T_i}{\int }}{h}_0\left(s\right)exp\{w_i+\alpha m_i\left(s\right)\}\right)\end{array}$                             (9)

To clearly define the baseline hazard one straight forward choice is exponential hazard function which was used in this study. Also by assuming normal distribution for random component the likelihood would be of form below:

$p(y_i\text{|}{u}_i;\theta )p(u_i;\theta )=\prod _{j}p\left\{y_i\left(t_{ij}\right)|u_i;{\theta }_y\right\}p(u_i;{\theta }_b)$

$=\prod _{j}p\left\{y_i\left(t_{ij}\right)|u_i;{\theta }_y\right\}\times {\left(2\pi \right)}^{-\frac{q_b}{2}}det{\left(D\right)}^{-\frac{1}{2}}exp(-u_i^T{D}^{-1}{u}_i/2)$

$=\left\{\prod _{t=1}^{n_i}\prod _{k=1}^K{\left({\pi }_{\text{ikt}}\right)}^{d_{ikt}}\right\}\times {\left(2\pi \right)}^{-\frac{q_b}{2}}det{\left(D\right)}^{-\frac{1}{2}}exp(-u_i^T{D}^{-1}{u}_i/2)$                     (10)

The logarithm of likelihood function $\mathcal{l}\left(\theta \right)=\sum _{i}logp({{\rm T}}_i.{\delta }_i.y_i;\theta )$ is maximized with respect to $\theta$ using a standard algorithm.^31,32

There are various optimization techniques for this likelihood function. Choosing an optimization algorithm depends on many factors for particular a problem that usually by trial and error can be achieved.^18,33-36 In this paper we used Conjugate Gradient algorithm to optimize the likelihood function.¹⁸ CONGRA algorithm is best for large problems where the objective function and the gradient can be computed much faster than the Hessian and where too much memory is required to store the (approximate) Hessian. Although this algorithm requires many iterations but each iteration can be much faster.³⁷ The main benefit of the technique is that the likelihood can be maximized straight forwardly by popular statistical packages such as SAS (Proc NLMIXED) which was used to estimate the parameters in this study. The inverse of Hessian matrix was computed to estimate the covariance matrix of the parameter estimates. Then the square root of the main diagonal entries of this matrix has given the standard error of each parameter.³⁷ Also, importance sampling utilizing gaussian quadrature method is used to approximate the integral likelihood function on random effects.³⁸ In this approach, obtaining the starting values the algorithm continue until converge with respect to the following criteria:¹⁸

$max\left\{|{\theta }^{\left(it\right)}-{\theta }^{(it-1)}|/(\left|{\theta }^{(it-1)}\right|+{ϵ}_1\right\}<{ϵ}_2$

$\mathcal{l}\left({\theta }^{\left(it\right)}\right)-\mathcal{l}\left({\theta }^{(it-1)}\right)<{ϵ}_3\{\left|\mathcal{l}\left({\theta }^{(it-1)}\right)\right|+{ϵ}_3\}$(11)

Where ${\theta }^{\left(\text{it}\right)}$ is the value of parameters in the i-th iteration of $\mathcal{l}\left(\theta \right)=\sum _{}logp(.{\delta }_i.y_i;\theta )$.

To address the conditions under which the model would perform optimally, the simulation study was designed by various scenarios to assess the effect of changing in sample size (n=100, 200 and 500) and amount of correlation (r=0.1, 0.3, 0.5) among longitudinal measurements in 100 Monte Carlo samples. A user defined code in SAS 9.4 was used to generate the data in time to event sub-model and the GenOrd Package in R was used to generate data in longitudinalsub-model.^39-41

To generate data in time to event sub-model, considering the exponential distribution for time to event, first the mean response was considered as a linear combination of $mu=b_{s_0}+b_{s_1}{X}_1$ in which the $b_{s_0}$ and$b_{s_1}$ are the intercept and slope of the regression. Also the covariate in the model is considered to be normally distributed $(X_1~N\left(0.1\right))$. Afterwards to define the event as a binary variable (1: event, 0: non-event), a uniform random variable with mean equal to the mean of the aforementioned exponential distribution ( $(u~U(L.U))$ ) so that for time to event values higher than the value of this variable the observation considered as censor.

In the longitudinal sub-model, the ordinal variables were generated by a determined correlation matrix and marginal distribution. The marginal distribution of the variables is related to one another by Copula function; in the first step, the Gaussian copula functions are constructed to achieve the desired correlation matrix of variables. Then in the next step, samples are generated from the target distribution. In the GenOrd Package, Pearson and Spearman correlation coefficients are available. Also, the agreement between defined correlation and observed correlation among generated data, are tested and the boundaries of acceptable correlations are provided for defined marginal distribution.⁴¹ Finally, the generated data for these sub-models are integrated in the SAS to fit the proposed joint model of time to event and ordinal longitudinal outcome.

The results of simulations are presented in Figure 1 and Figure 2 considering bias, bias percentage and mean square of error (MSE) as the measure of evaluation.⁴² The charts of Figure 1 showed that by increasing the sample size, bias, bias percentage and MSE is reduced in constant correlation among longitudinal measurements scenario. In particular, for n=50 to the other samples, bias, bias and MSE of the difference is obvious more. Also, according to the charts of Figure 2, mostly by increasing the correlation among longitudinal measurements, bias, bias percentage and MSE is reduced in constant sample size scenario.

Figure 1 The charts of bias, bias percentage and MSE of parameters by increasing the sample size in constant correlation among longitudinal measurements scenario.

Figure 2 The charts of bias, bias percentage and MSE of parameters by increasing correlation among longitudinal measurements in constant sample size scenario.

Hypertension is one of the most important modifiable risk factors for coronary heart diseases and problems are significant negative consequences on health and economy as well.⁴³ studies show that treatment and control of hypertension can reduce the risk of cardiovascular disease and its complications.^44-47 With respect to the blood pressure (BP) is changing with over time and life styles, thus the regular monitoring of these repeated measurements provide more useful information than a single measurement. In addition, the intervention and control other risk factors that affect both hypertension and CHD, is of great importance. Typically, classical modeling does not consider dependencies between longitudinal measures of anthropometric indices and CHD incidence. Therefore, in this study we utilized a joint modeling of longitudinal measures of BP levels and CHD risk, to know whether this outcome can be a significant indicator of predicting CHD incidence.

This study was performed under the framework of the Tehran Lipid and Glucose Study (TLGS), a community-based longitudinal study in four phases (phase I: (1999-2001), phase II: (2002-2005), phase III: (2006-2008) and phase IV: (2009-2011)), from district 13 of Tehran, the capital city of Iran. A multistage cluster random sampling technique was used to select more than 15000 people ages> 3y. All participants were followed for any hospitalized or death event annually up to 20 March 2012.⁴⁸

In the current study, we first considered all participants age≥30 years and excluded individuals with a history of Cardio Vascular Disease (CVD) or stroke (n=487), participants without any blood pressure data (n=32), and subjects without follow-up of Coronary Heart Diseases (CHD) (n=715). Finally, 3784 women and 2889 men were recruited into the study. Informed written consent was obtained from all participants. The study was approved by the ethics committee of the Research Institute for Endocrine Sciences, Shahid Beheshti University of Medical Sciences, Tehran, Iran.

For the measurement of the ordinal longitudinal variable (BP), definitions and classification is based on ESH/ESC Guidelines for the management of arterial hypertension levels (optimal, normal, high normal and hypertension).⁴⁹ Also coronary heart disease, as the time to event outcome of this study was definite as myocardial infarction, unstable angina pectoris, angiography proven CHD and CHD death. All of them are comparable with ICD10 rubric I20–I25. The event and its corresponding date were confirmed by an outcome committee.⁴⁸ Baseline covariates included in joint model are as follows: the high risk age group, ages 45 and 55 years or higher in men and women respectively; Body Mass Index (BMI) was calculated weight (kg) divided by the square of the height (m²); hypercholesterolemia, serum cholesterol ≥6.2 mmol/l (240 mg/dl) or taking cholesterol lowering medication;; diabetes, fasting plasma glucose ≥7.0 mmol/l (126 mg/dl) or 2 hours post load glucose ≥11.1 mmol/l (200 mg/dl) or taking any medication for diabetes; low HDL cholesterol, HDL cholesterol <1.03 mmol/l (40 mg/dl);tobacco consumption, any tobacco product (cigarette, pipe, water pipe) in the past or currently on a regular or occasional basis; family history of CVD, history of myocardial infarction or stroke or sudden cardiac death in a male first degree relative <55 years or female first degree relative <65 and the high risk age group, ages 45 and 55 years or higher in men and women respectively. Details of data collection in TLGS have been published previously (48).

Figure 3 presents Kaplan-Meier estimates of survival time separated by sex and blood pressure levels in four Phase. It shows that the men at every level of blood pressure were more likely to have CHD than women were the same level of blood pressure. We have used the following CLM, CRM and CPM longitudinal and time to event model to analyze the data set. Wu-Hausman Specification Test is used to choose between fixed effects model or a random effects model in the analysis of data over time(50).CLM mixed effects model with random intercept and random slope is

$\begin{array}{l}logit\left(P(B{P}_i\left(t\right)\le k)\right)=log\left[\frac{P(B{P}_i\left(t\right)\le k)}{1-P(B{P}_i\left(t\right)\le k)}\right]\\ ={\alpha }_k\\ -\left[\begin{array}{l}{{\beta }^{\text{'}}}_1+{{\beta }^{\text{'}}}_2\times Phas{e}_i+{{\beta }^{\text{'}}}_3\times Ag{e}_i+{{\beta }^{\text{'}}}_4\times FamilyHist+{{\beta }^{\text{'}}}_5\times tobacus{e}_i+\\ {{\beta }^{\text{'}}}_6\times Diabete{s}_i+{{\beta }^{\text{'}}}_7\times BM{I}_i+{{\beta }^{\text{'}}}_8\times CHO{L}_i+{{\beta }^{\text{'}}}_9\times HD{L}_i+{U^{\text{'}}}_{1i}+\times Phas{e}_i\end{array}\right]k=\mathrm{1.2.3.} \end{array}$(12)

CRM mixed effects model with random intercept and random slope is

$\begin{array}{l}logit\left(P(B{P}_i\left(t\right)=k|Y\ge k)\right)=log\left[\frac{P(B{P}_i\left(t\right)=k|Y\ge k)}{1-P(B{P}_i\left(t\right)=k|Y\ge k)}\right]\\ ={\alpha }_k\\ -\left[\begin{array}{l}{{\beta }^{\text{'}}}_1+{{\beta }^{\text{'}}}_2\times Phas{e}_i+{{\beta }^{\text{'}}}_3\times Ag{e}_i+{{\beta }^{\text{'}}}_4\times FamilyHist+{{\beta }^{\text{'}}}_5\times tobacus{e}_i+\\ {{\beta }^{\text{'}}}_6\times Diabete{s}_i+{{\beta }^{\text{'}}}_7\times BM{I}_i+{{\beta }^{\text{'}}}_8\times CHO{L}_i+{{\beta }^{\text{'}}}_9\times HD{L}_i+{U^{\text{'}}}_{1i}+{U^{\text{'}}}_{2i}\times Phas{e}_i\end{array}\right]k=\mathrm{1.2.3.}\end{array}$            (13)

CPM mixed effects model with random intercept and random slope is

$\begin{array}{l}{\Phi }^{-1}\left(P(B{P}_i\left(t\right)\le k)\right)\\ ={\alpha }_k\\ -\left[\begin{array}{l}{{\beta }^{\text{'}}}_1+{{\beta }^{\text{'}}}_2\times Phas{e}_i+{{\beta }^{\text{'}}}_3\times Ag{e}_i+{{\beta }^{\text{'}}}_4\times FamilyHist+{{\beta }^{\text{'}}}_5\times tobacus{e}_i+\\ {{\beta }^{\text{'}}}_6\times Diabete{s}_i+{{\beta }^{\text{'}}}_7\times BM{I}_i+{{\beta }^{\text{'}}}_8\times CHO{L}_i+{{\beta }^{\text{'}}}_9\times HD{L}_i+{U^{\text{'}}}_{1i}+{U^{\text{'}}}_{2i}\times Phas{e}_i\end{array}\right]k=\mathrm{1.2.3.}\end{array}$(14)

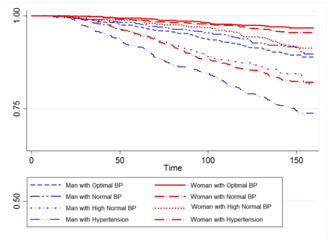
                     Phase I                                           Phase II

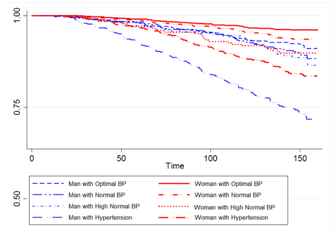
                        Phase III                                           Phase IV

Figure 3 Estimated of Kaplan-Meier survival functions by sex and blood pressure levels in four Phases.

And, for the time to event data, using (5), we have considered a relative risk regression with the exponential function for baseline (according to Anderson-Darling Test) and with proportionality assumption (according to Therneau's Test).

Table 1 shows the results of the joint modeling on the data set. Three longitudinal models are compared using AIC and C criteria which show that the CRM model has the better fit to the data and a decline in standard error estimates. Also the obtained results from joint modeling showed that the risk of coronary heart diseases increases about 20% and 44% times in females and males, respectively, with increasing one level of the blood pressure (P<0.001).

The joint modeling of longitudinal and time-to-event data is a progressing area of statistical research thathas been used extensively in recent years.^51,54 Thismodels also can be used when the main aim of the research is on longitudinal analysis with non-random dropout, and in cases where the target is on survival analysis with consideration of an endogenous time-dependent covariate.⁵⁵ Andrinopoulou et al. suggested a joint model to investigate the degree of association between the trend of the repeated measures of aortic gradient and aortic regurgitation and time-to-events of death and reoperation.⁵⁶

Concerning the endogenous nature of the ordinal longitudinal measures the two stage modeling, as utilized by other studies^3,57,58 didn’t perform in our data well (as indicated by AIC). In such cases, since the models can’t be taking into account the measurement error in time dependent covariates, therefore the estimates of parameters are biased.¹⁰

In this study, the proposed model covers existing methods to handle longitudinal ordinal data using proportional odds models including cumulative logit, probit and continuation ratio models. As identified by Agresti¹⁵ in our data with sequential mechanism the latest model perform better than the others based on AIC. On the other hand, the estimates provided by this model is rather smaller than those provided by cumulative logit and probit models because this model estimates the probability in a defined category with respect to lower or higher order categories while in the probit or cumulative logit models, the probabilities are estimated in global scale.

Additionally, considering AIC and Cox Snell residuals, the exponential model had better fit in this data (results not shown). In this case the inferences are more accurate than the semi parametric cox model.^59,60

Importance sampling procedure was carried out as a simple and effective approach to optimize model’s numerical integration and one of its advantages is the utilizing standard statistical packages such as PROC NLMIXED in SAS. Comparing to other integration approaches, importance sampling technique is a suitable procedure and one of its advantages is the utilizing standard statistical packages such as PROC NLMIXED in SAS to maximize the likelihood easily.¹⁹ NLMIXED is the powerful computational procedure to optimize linear and nonlinear models with normal random effects including various optimization algorithms.³⁷

There was a substantial computation in the models provided; hence the “CONGRA” algorithm was used to optimize the models. The first-derivative method CONGRA is paramount for large computations where the objective function and the gradient can be subtracted much faster than the Hessian and where high amount of memory is required to save the Hessian matrix.³⁷

Also, our simulation study showed that by increasing the sample size as well as correlations among ordinal longitudinal measures, the bias and mean square error of the parameter estimates have improved. These finding are in the line with those found by others,^42,61 which can be reasoned by greater amount of heterogeneity in subjects along with higher correlations among longitudinal measurements. In the joint model with random effect, the independence of time to event and longitudinal process is being guaranteed by conditioned on random effect.⁶²

The values of ​​association parameter (α) is shown a significant association between changes in the two outcomes (P<0.001). In other words, that the risk of coronary heart diseases increases about 23% and 46% times in females and males, respectively, with increasing one level of the blood pressure. If Player and colleagues review, which aims to investigate the relationship between hypertension and cardiovascular disease was conducted, the results showed that with increased incidence of hypertension, the risk of cardiovascular disease increases.⁶³ In a meta-analysis of 68 clinical exam and a 10-year follow-up period, it was shown that mmHg10 reduction in systolic blood pressure or diastolic blood pressure and reduce the incidence of cardiovascular disease is.⁶⁴

One of the main shortcomings of joint models especially those proposed in this model, is the low convergence of corresponding algorithms and hence needing to high amount of computational power. Future direction in this regard can be proposed to investigate faster algorithm and specific software to implement this technique.

Also, the models can be adopted to cover the competing risks in the time to event sub- model. In addition, the longitudinal process is usually multifactorial and can be measured in the multivariate framework and the can be assessed in the longitudinal sub-modelin multivariate fashion.

Taking into account the prior information on parameter estimate as well as to achieve the exact inferences especially in smaller sample size, bayesian form of the proposed models are recommended to be investigated.

The authors acknowledge the TLGS participants and field investigators for their assistance in physical examinations, biochemical and database management.

The authors declare that there are no conflicts of interest.

1. Ibrahim JG, Chu H, Chen LM. Basic concepts and methods for joint models of longitudinal and survival data. Journal of Clinical Oncology. 2010;28(16):2796–2801.
2. Cox DR. Regression models and life–tables. Breakthroughs in statistics: Springer. 1992;527–541.
3. Self S, Pawitan Y. Modeling a marker of disease progression and onset of disease.  AIDS Epidemiology: Springer; 1992:231–255.
4. Proust–Lima C, Séne M, Taylor JM, et al. Joint latent class models for longitudinal and time–to–event data: A review. Stat Methods Med Res. 2014;23(1):74–90.
5. Wu L, Liu W, Yi GY, Huang Y. Analysis of longitudinal and survival data: joint modeling, inference methods, and issues. Journal of Probability and Statistics. 2011;2012.
6. Rizopoulos D. Joint models for longitudinal and time–to–event data: With applications in R: CRC Press. 2012.
7. McCrink L, Marshall AH, Cairns K, et al. editors. Joint modelling of longitudinal and survival data: A comparison of joint and independent models. 58th ISI World Statistical Congress. 2011.
8. Schluchter MD. Methods for the analysis of informatively censored longitudinal data. Statistics in medicine. 1992;11(14‐15):1861–1870.
9. Tsiatis AA, Davidian M. Joint modeling of longitudinal and time–to–event data: an overview. Statistica Sinica. 2004;14(3):809–834.
10. Fieuws S, Verbeke G. Joint modelling of multivariate longitudinal profiles: pitfalls of the random‐effects approach. Statistics in medicine. 2004;23(20):3093–3104.
11. Chakraborty A. Bounded influence function based inference in joint modelling of ordinal partial linear model and accelerated failure time model. Statistical methods in medical research. 2014:0962280214531570.
12. Armero C, Forné C, Rué M, et al. Bayesian joint ordinal and survival modeling for breast cancer risk assessment. Stat Med. 2016;35(28):5267–5282.
13. Rué M, Andrinopoulou ER, Alvares D, et al. Bayesian joint modeling of bivariate longitudinal and competing risks data: An application to study patient‐ventilator asynchronies in critical care patients. Biom J. 2017;59(6):1184–1203.
14. Li N, Elashoff RM, Li G, et al. Joint modeling of longitudinal ordinal data and competing risks survival times and analysis of the NINDS rt‐PA stroke trial. Stat Med. 2010;29(5):546–557.
15. Agresti A. Analysis of ordinal categorical data: John Wiley & Sons; 2010.
16. Harrell Jr FE. Parametric survival models.  Regression Modeling Strategies: Springer.2001;413–442.
17. Harrell F. Regression modeling strategies: with applications to linear models, logistic and ordinal regression, and survival analysis. Springer; 2015.
18. Powell MJD. Restart procedures for the conjugate gradient method. Mathematical programming. 1977;12(1):241–254.
19. Pinheiro JC, Bates DM. Approximations to the log–likelihood function in the nonlinear mixed–effects model. Journal of computational and Graphical Statistics. 1995;4(1):12–35.
20. Hosmer Jr DW, Lemeshow S, Sturdivant RX. Applied logistic regression: John Wiley & Sons; 2013.
21. Fagerland MW, Hosmer DW. Tests for goodness of fit in ordinal logistic regression models. Journal of Statistical Computation and Simulation. 2016;86(17):3398–3418.
22. Cagnone S, Mignani S, Moustaki I. Latent variable models for ordinal data.  Statistical Methods for the Evaluation of Educational Services and Quality of Products. Springer; 2009;17–28.
23. Zeng D, Cai J. Simultaneous modelling of survival and longitudinal data with an application to repeated quality of life measures. Lifetime Data Analysis. 2005;11(2):151–174.
24. Chi YY, Ibrahim JG. Joint models for multivariate longitudinal and multivariate survival data. Biometrics. 2006;62(2):432–445.
25. Hanson TE, Branscum AJ, Johnson WO. Predictive comparison of joint longitudinal–survival modeling: a case study illustrating competing approaches. Lifetime data analysis. 2011;17(1):3–28.
26. R Brown E, G Ibrahim J. A Bayesian semiparametric joint hierarchical model for longitudinal and survival data. Biometrics. 2003;59(2):221–228.
27. Wang Y, Taylor JMG. Jointly modeling longitudinal and event time data with application to acquired immunodeficiency syndrome. Journal of the American Statistical Association. 2001;96(455):895–905.
28. Xu J, Zeger SL. Joint analysis of longitudinal data comprising repeated measures and times to events. Journal of the Royal Statistical Society: Series C (Applied Statistics). 2001;50(3):375–387.
29. Henderson R, Diggle P, Dobson A. Joint modelling of longitudinal measurements and event time data. Biostatistics. 2000;1(4):465–480.
30. Hsieh F, Tseng YK, Wang JL. Joint modeling of survival and longitudinal data: likelihood approach revisited. Biometrics. 2006;62(4):1037–1043.
31. Vila J, Schniter P. editors. Expectation–maximization Bernoulli–Gaussian approximate message passing. Signals, Systems and Computers (ASILOMAR), 2011 Conference Record of the Forty Fifth Asilomar Conference on. IEEE. 2011.
32. Lange K. Elementary optimization. Optimization: Springer. 2004;1–17.
33. Fujiwara K, Okamoto Y, Kameari A, et al. The Newton–Raphson method accelerated by using a line search–comparison between energy functional and residual minimization. IEEE transactions on magnetics. 2005;41(5):1724–1727.
34. Geyer CJ. Trust region optimization. 2015.
35. Dennis J, John E, Moré JJ. Quasi–Newton methods, motivation and theory. SIAM review. 1977;19(1):46–89.
36. Zhu J. Optimization of power system operation: John Wiley & Sons; 2015.
37. Wolfinger RD. editor. Fitting nonlinear mixed models with the new NLMIXED procedure. Proceedings of the 24th Annual SAS Users Group International Conference (SUGI 24). 1999.
38. Pinheiro JC, Bates DM. Mixed–effects Models in S and S–PLUS. New York: Springer–Verlag. 2000.
39. Lee A. Some simple methods for generating correlated categorical variates. Computational statistics & data analysis. 1997;26(2):133–148.
40. Ibrahim NA, Suliadi S. Generating correlated discrete ordinal data using R and SAS IML. Computer methods and programs in biomedicine. 2011;104(3):e122–e132.
41. Ferrari PA, Barbiero A. Simulating ordinal data. 2012;47(4):566–589.
42. Hasle H, Boldsen JL. Childhood conditions and adult height. Journal of biosocial science. 1991;23(01):107–112.
43. Hall JE, Granger JP, Carmo JM, et al. Hypertension: physiology and pathophysiology. Compr Physiol. 2012.
44. James PA, Oparil S, Carter BL, et al. 2014 Evidence–based guideline for the management of high blood pressure in adults: report from the panel members appointed to the Eighth Joint National Committee (JNC 8). JAMA. 2014;311(5):507–520.
45. Collaboration BPLTT. Blood pressure–lowering treatment based on cardiovascular risk: a meta–analysis of individual patient data. The Lancet. 2014;384(9943):591–598.
46. Peterson ED, Gaziano JM, Greenland P. Recommendations for treating hypertension: what are the right goals and purposes? JAMA. 2014;311(5):474–476.
47. Ghoreishian H, Tohidi M, Derakhshan A, et al. Presence of hypertension modifies the impact of insulin resistance on incident cardiovascular disease in a Middle Eastern population: the Tehran Lipid and Glucose Study. Diabet Med. 2015.
48. Khalili D, Sheikholeslami FH, Bakhtiyari M, et al. The Incidence of Coronary Heart Disease and the Population Attributable Fraction of Its Risk Factors in Tehran: A 10–Year Population–Based Cohort Study. PloS One. 2014;9(8):e105804.
49. Mancia G, De Backer G, Dominiczak A, et al. 2007 ESH–ESC practice guidelines for the management of arterial hypertension: ESH–ESC task force on the management of arterial hypertension. Journal of hypertension. 2007;25(9):1751–1762.
50. Nakamura A, Nakamura M. On the relationships among several specification error tests presented by Durbin, Wu, and Hausman. Econometrica: journal of the Econometric Society. 1981;49(6):1583–1588.
51. Crowther MJ. Development and application of methodology for the parametric analysis of complex survival and joint longitudinal–survival data in biomedical research. Department of Health Sciences. 2015;1–261.
52. Ekinci EI, Moran JL, Thomas MC, et al. Relationship Between Urinary Sodium Excretion Over Time and Mortality in Type 2 Diabetes. Diabetes care. 2014;37(4):e62–e63.
53. Njagi EN, Rizopoulos D, Molenberghs G, et al. A joint survival–longitudinal modelling approach for the dynamic prediction of rehospitalization in telemonitored chronic heart failure patients. Statistical Modelling. 2013;13(3):179–198.
54. Zangwill LM, Boer ER, Weinreb RN, et al. Association Between Progressive Retinal Nerve Fiber Layer Loss and Longitudinal Change in Quality of Life in Glaucoma. JAMA Ophthalmol. 2015;133(4):384–390.
55. Barrett J, Diggle P, Henderson R, et al. Joint modelling of repeated measurements and time‐to‐event outcomes: flexible model specification and exact likelihood inference. J R Stat Soc Series B Stat Methodol. 2015;77(1):131–148.
56. Andrinopoulou ER, Rizopoulos D, Geleijnse ML, et al. Dynamic prediction of outcome for patients with severe aortic stenosis: application of joint models for longitudinal and time–to–event data. BMC cardiovascular disorders. 2015;15(1):28.
57. Tsiatis A, Degruttola V, Wulfsohn M. Modeling the relationship of survival to longitudinal data measured with error. Applications to survival and CD4 counts in patients with AIDS. Journal of the American Statistical Association. 1995;90(429):27–37.
58. De Gruttola V, Tu XM. Modelling progression of CD4–lymphocyte count and its relationship to survival time. Biometrics. 1994;50(4):1003–1014.
59. Miller Jr RG. Survival analysis. John Wiley & Sons; 2011.
60. Oakes D. The asymptotic information in censored survival data. Biometrika.1977;64(3):441–448.
61. Reinecke J. Structural equation models in the social sciences. Walter de Gruyter GmbH & Co KG; 2014.
62. Henderson R. Joint modeling of longitudinal and event time data. Encyclopedia of Biostatistics. 2005.
63. Player MS, Peterson LE. Anxiety disorders, hypertension, and cardiovascular risk: a review. Int J Psychiatry Med. 2011;41(4):365–377.
64. Thomopoulos C, Parati G, Zanchetti A. Effects of blood pressure lowering on outcome incidence in hypertension. Journal of Hypertension. 2015;33(2):195–211.