National health systems are vital for ensuring equitable healthcare access and societal well-being. Despite their objectives, such as disease treatment, health promotion, financial sustainability, and quality services, they face complex challenges, particularly in health care access. Portugal's National Health System (NHS) is strained by an increasing and aging population.

This paper, using a 2019 official database, just analyzes the human resources available in public hospitals at subregions level (NUTS III) and one critical outcome related to the surgical activity of these nuclear health units covering thirteen main specialties. Cluster analysis proved to be an effective statistical methodology to detect disparities between regions across the country. Key finding revealed Coimbra Region as having the best health’s human resources followed by two metropolitan areas of Lisboa and Porto in contrast to most of the surrounding subregions.

This investigation underscores the need for target health policies to improve resource distribution within Portugal’s NHS.

Keywords: cluster analysis, healthcare services, health indicators, national health service, Portugal

National Health systems are crucial for the society’s well-being and health as it provides equity in accessing healthcare.^1,2

National health systems are complex and have some fundamental objectives. Besides the treatment of diseases these systems also need to focus on Health promotion and disease prevention, financial sustainability, ability to respond to population expectations and good quality services.^3–7

Despite the efforts, recent studies have demonstrated that National Health systems haven’t totally met their objectives reporting issues in health access.⁸ Authors such as⁹ find it imperative to evaluate healthcare systems to improve their functionality. And access to full statistical information is a critical restriction to such evaluation.

Population growth and ageing are demographic phenomena that have significant implications for health systems around the world.^10,11

According to Statistics Portugal,¹² the estimated resident population in Portugal in 2023 was 10.639.726, 120.000 more people compared to 2022. There is a noticeable upward trend, with this estimate of the resident population having risen for the fifth consecutive year. In 2023, Portugal´s ageing population continued to increase. The National Health System (NHS) is facing growing challenges due to these demographic changes. This study is relevant because it assesses the capacity of the NHS to respond to the needs of a growing and ageing population, identifying areas in need of improvement. It is just a preliminary research covering two main areas of NHS statistical data.

This study will examine a 2019 official database that INE made available after conducting a survey of Portuguese hospitals. This year was chosen over 2020 and 2021, as they are years affected by the pandemic. This database has multiple variables representative of various aspects of a national health system, such as variables on health professionals, the number of surgeries performed or the number of medical consultations performed, among others. The aim of this study is to evaluate data from NHS hospitals to identify asymmetries in the distribution of resources and services available in the different regions of the country. This will give us a global view of the state of the country, while understanding in detail the needs of each region.

We will study this data through a cluster analysis, also aiming to explore the state of the art of this methodology. Using different approaches, from various forms of data standardization, different agglomeration methods to different cluster analysis methods, the objective is to demonstrate its applicability and relevance in the treatment of different types of data, in the area of health.

Contextualization

On the 15 September 1979, Portugal established their National Health Service (NHS). This date is an important mark on Portugal's public healthcare history because it marked the establishment of a universal and free system that covers all residents - cementing health as an underlying right.¹³

At its foundation, NHS made evident its expansion and improvement of services as well as accessibility to provide universal, quality healthcare. Over recent decades it faced increasing population ageing and chronic disease prevalence that required it to focus more heavily on primary health care management and disease prevention; reforms included new management models to enhance efficiency as well as the creation of Executive Board of NHS.

At September of 2022 the Portuguese government established the organizational structure for Executive Board of NHS. Their primary responsibility lies with coordinating the Care provided by healthcare units of NHS. One of the most significant reforms implemented by this administration was the Local Health Units (LHU).

These Units play a vital role in the reorganization of the National Health Service (NHS). The LHU, first limited to specific regions, has now been extended to include the entire country, facilitating unified administration that combines hospital centers, hospitals, Health Center Clusters (HCC), and the National Network of Continuing Care within a particular geographic zone.

The LHU paradigm enables greater autonomy and efficiency in the administration of healthcare services. The primary objective of the NHS is to maximize resource utilization, promote continuity of care and ensure a comprehensive strategy that covers all aspects of healthcare, starting from preventive measures to rehabilitation. These LHU reinforce the idea that health extends beyond hospital treatment by additionally emphasizing the importance of primary care.

NHS draws its model from UK´s National Health Service, in which state providers ensure universal, generalized, and tendentially free health coverage; at the same time allowing free medicine as an adjunct or complementary care option. This is a Beveridge's Model funded via State Budget. This type of financing is linked directly with macroeconomic indicators, meaning its allocation towards health would depend upon both growth in Gross Domestic Product (PIB) as well as percentage of expenditure allocated towards health in relation to GDP. This percentage is very vulnerable to political and strategic decisions.

Therefore, our study will focus on discussing and providing indicators essential for hospital evaluation. These metrics will play a central role in our future research, not only in measuring the efficiency of resource utilization but also ensuring that, regardless of financial limits, quality and efficacy standards in health care service delivery remain at or exceed minimum levels. The increasing access to outcome health indicators will be the key to an expected increase in NHS’s performance during the next years.

The nuts system in Portugal

The Nomenclature of Territorial Units for Statistics (NUTS) is a defined geographical classification used by the European Union to collect, develop, and harmonize regional statistics. The NUTS system is organized into three hierarchical levels: NUTS I, NUTS II, and NUTS III. The regions in each level are presented in table 1 and figure 1 and follows the NUTS 2013 categorization.¹⁴

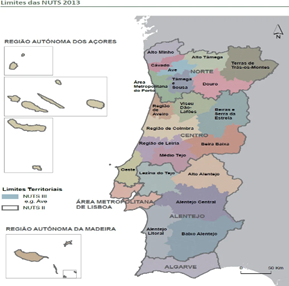
Figure 1 Geographical layout of the twenty-five NUTS III.¹⁴

Health indicators

The assessment and improvement of healthcare services relies heavily on the use of health indicators to measure the quality and efficiency of hospitals. These indicators are crucial instruments for assessing hospital performance, promoting responsibility, and directing quality improvement programs within healthcare organizations. By monitoring key performance indicators (KPIs), hospitals can track their progress, identify areas for improvement, and guarantee the delivery of high-quality care to patients.¹⁵

The quality of treatment offered to patients is substantially influenced by human resources factors. An analysis of factors such as staffing levels, staff training, and specialists with different skills helps in finding areas that can be enhanced to provide care that is safe, efficient, and focused on the needs of the patient. Maintaining high-quality healthcare services requires having an enough number of employees and highly qualified personnel.¹⁶

Healthcare access indicators have a significant impact on the outcomes of public health. Enhanced access to preventative services, screenings, and treatments can result in improved overall health of the population and prevention of diseases. Through the analysis of access indicators, public health interventions can be focused on increasing access to vital healthcare services and promoting general well-being.¹⁷

Introduction

Cluster analysis has been widely employed in health-related studies to find homogeneous groups within populations based on several factors. This methodology enables researchers to identify patterns and relationships within health data that may not be immediately apparent, thereby offering significant insights on health care needs, service utilization and the overall system performance.^18-22

Conducted a study that applied cluster analysis to evaluate the primary healthcare performance in municipalities, emphasizing the importance of identifying critical areas and groups with greater health needs.²¹

Performed a study where they applied cluster analysis to evaluate health indicators and expenditures among European countries. The research showcased the utility of cluster analysis in health system performance evaluation by grouping countries with similar health profiles and spending patterns.¹⁹

In their study,²⁰ used cluster analysis to discover unmet healthcare needs among rheumatoid arthritis patients, demonstrating the capacity of this method to investigate healthcare disparities.

Applied cluster techniques to categorize European healthcare systems into three types based on financing, service provision, and access to healthcare ²²

In Portugal,¹⁸ utilized cluster analysis to investigate multimorbidity trends among prostate cancer patients admitted to hospitals in Portugal.

These studies collectively demonstrate the versatility of cluster analysis in health research, from the assessment of healthcare performance, comprehension of service consumption patterns, and identification of unmet healthcare needs. This methodology is a valuable technique for healthcare researchers and policymakers to discover hidden patterns, assess the effectiveness of the system, and develop targeted approaches.

Cluster analyses

Cluster Analysis, or Clustering, is the process of organizing a set of objects into homogenous groups, known as clusters, so that objects in the same cluster share many characteristics but are very dissimilar to objects in the other clusters.²³

Clustering models are distance based algorithms so the measure of dissimilarities between observations, or group of observations, use a distance metric and variables with a high range would have a strong influence on the clustering. This is why a previous standardization of data will be considered. Anyway, the loss of information inherent to such transformations would be limited if the clustering process is preceded by univariate exploratory data analysis.

Mixed variables

Researchers have developed multiple approaches and algorithms to calculate dissimilarities on mixed data, since it’s very likeable in real data scenarios to have both numerical and categorial attributes.^24,25

The “Romesburg approach” suggests that the variables nature should be ignored, and they all should be treated as quantitative, encoding those that are qualitative. Subsequently, it´s just a matter of choosing an appropriate coefficient for the quantitative variables, like the Euclidean distance. However, the interpretation of the similarity coefficients is difficult, due to its dependence on the chosen coding for the qualitative variables.

“Perform separate analysis” consists of creating a similarity measure for each set of variables of the same type and conducting distinct cluster analysis for each group. If the results indicate consensus, it means that this approach can be implemented. If consensus is not reached, the general procedure is to perform a single cluster analysis with all the data together “reducing all variables to binary variables” is another approach that can be implemented for quantitative variables, by dividing the domain of each variable into two blocks and applying the following rule:

${\text{If y}}_{\text{ij}}<{\text{c}}_{\text{j}},{\text{ then x}}_{\text{ij}}=0;$

${\text{If y}}_{\text{ij}}\ge {\text{c}}_{\text{j}},{\text{ then x}}_{\text{ij}}=1$

where $y_{ij}$ is the original variable j in object i, the $c_j$  it’s the critical value that divides the domain of the variable j. The new binary variable is represented by $x_{ij}$  for the object i.

A disadvantage of this approach is the loss of information when converting complete data into a binary form²⁶ presented the combined similarity coefficient, given by

$s_{ij}=\frac{{{\displaystyle \sum }}_{k=1}^p{\omega }_{ijk}{s}_{ijk}}{{{\displaystyle \sum }}_{k=1}^p{\omega }_{ijk}},$

where $s_{ijk}$  is the similarity between objects i and j based on variable k. Normally, the variable ${\omega }_{ijk}$  is 1 or 0 if the comparison between values i and j is valid or not valid, meaning that the value of the variable k is missing in at least one of the objects i and j.

When the variables are binary or nominal with more than two levels, the coefficients $s_{ijk}$  is equal to 1 if the two objects have the same value in variable k and is equal to 0 otherwise.

For continuous variables, Gower suggests using the similarity coefficient based on the Standardize Manhattan metric for variable k,

$s_{ijk}=1-\frac{\left|x_{ik}-x_{jk}\right|}{R_k},$   where $R_k$  is the range of variable K.

In this paper, the objects are the local medical Units, and it will be analyzed which variables they have in common to stay in the same cluster and understand what makes clusters heterogeneous, considering the set of variables for which they are targeted.

The application of cluster analysis involved two main methods, these can be either Hierarchical or non-Hierarchical.

Hierarchical methods

Hierarchical clustering methods identify subgroups within a dataset by organizing them into a hierarchical structure based on measures of dissimilarity or distance. They are particularly useful for understanding the underlying structure of the data and for visualizing the relationships between the analyzed objects. There are two main algorithms, ascending and descending.²⁷

The hierarchical structure resulting from these procedures is represented in a two-dimensional graph called Dendrogram also named Value Tree.²⁸

The ascending hierarchical classification methods are the most popular and widely used and will be the ones used in this paper.

The initial objects are singular clusters, and each step will aggregate the two most similar groups, so with the smallest dissimilarity. And the procedure is repeated until a single group is formed.

The question that arises is how to define the distance between two groups. There are several proposals, and each one provides a different hierarchical agglomerative method, namely the single linkage, the complete linkage, the group average method and ward method.

Non-hierarchical methods

This method is sensitive to the initialization about the number of clusters, in some way suggested by previous hierarchical cluster analysis.

The elbow method is a popular approach for selecting the value of the number of clusters, it involves the creation of a plot with the number of clusters on the x-asis and the total within sum of squares on the y-axis. The objective is to determine the point in the plot where a “elbow” or bend occurs.²⁹

Another known method is the Silhouette one, where each cluster is represented by a silhouette identifying which objects lie quite well within the cluster and the objects that present an intermediate position. So, the entire clustering is explained by plotting all the silhouettes into a single diagram, allowing the comparison of the quality of the clusters.³⁰

Considering a cluster A and $\text{a}\left(\text{i}\right)$ as being the average dissimilarity of i to all the other objects of A.

For any Cluster C different of A, $d\left(i,C\right)$  can be defined as the average dissimilarity of i to all the objects of C.

$\text{Let b}\left(\text{i}\right)=\min \text{d}\left(\text{i},\text{C}\right)),\text{ when }\left[\text{C}\ne \text{A}\right]$

and the silhouette can be defined by

$\text{S}\left(\text{i}\right)=\frac{\text{b}\left(\text{i}\right)-\text{a}\left(\text{i}\right)}{\max \{\text{a}\left(\text{i}\right),\text{b}\left(\text{i}\right)\}}$

When $\text{S}\left(\text{i}\right)$  is at it´s largest, this will mean that the within dissimilarity $\text{a}\left(\text{i}\right)$ is much smaller than the smallest dissimilarity $\text{b}\left(\text{i}\right)$ .

From such definition we have $-1\le \text{S}\left(\text{i}\right)\le 1\text{ for each object i }$

This method can be used to identify the number of clusters by the following process.

Firstly, the specified algorithm should be run multiple times, each with a different number of clusters k. Secondly, for each clustering solution the silhouette score for every data point in the dataset should be calculated. The next is to calculate the average silhouette score for each clustering solution. This provides a single value representing the overall quality of clustering for each k. Then it´s necessary to construct a graph that displays the number of clusters on the x-axis and the average silhouette score on the y-axis. The last step is to identify the highest point in the plot, that represents the “optimal” number of clusters.

The most common non-hierarchical clustering method is designated K-Means.

The K-means algorithm is a technique for clustering that seeks to divide n observations into k clusters, ensuring each observation is grouped with the cluster whose mean is closest. Initially, points $c_1,c_2,\dots ,c_k$ are placed randomly within the dataset to be clustered, with various methods available for determining these initial placements. Every observation is then allocated to the nearest cluster based on proximity to each ${\text{ c}}_{\text{j}}$ . In a subsequent step, these initial points are substituted with the centroids of the clusters they represent, and the process of associating observations to clusters is iterated. The algorithm reaches an optimal state when there are no further changes in these centroids or when a predefined number of iterations is attained.²⁹

Although this method is simple to implement and suitable for large data sets, it has some disadvantages, such as its lack of robustness since it uses the average of each cluster. Another disadvantage is that the possible presence of outliers can greatly distort the distribution of the data. The fact that it is necessary to predefine several clusters can be a disadvantage if the structure of the data is not known.

The k-medoids algorithm has the same purpose of the K-means algorithm, however, while the last one uses the mean of the data points to establish cluster centers, the K-medoids, uses the actual data points as representatives of the clusters. These data points are known as medoids. Additionally, this algorithm can be applied with any dissimilarity measures, while K-means generally depends on Euclidean distance for optimal solutions. K-medoids algorithm is more robust to outliers and noise in the dataset, since its property of being less affected by extreme values.³¹

The “dynamic clusters” method proposed by³² (Ref.ª) is an extension of the K-means method - instead of representing a class by its center of gravity, it is represented by a "nucleus", a set of k points, generally the most central ones. Formally, a representation function is defined which associates a set of points with the respective nucleus.

The algorithm then develops by alternately considering the phases of assignment and representation until its convergence of the predefined criterion. The final partition depends on the initial selection of nuclei, for which Diday proposed performing $x$  initializations. "Stable clusters" are defined as the sets of elements that remain grouped in the $x$  repetitions of the algorithm. One advantage of this dynamic cluster’s method is the ability to use other distances besides Euclidean distances.

Data set

The database organizes the data into 25 NUTS III (Figure 2, Table 2).

Figure 2 Dendrogram using ward´s Method.

The data refers to 2019. Due to some data being reported jointly by a certain hospital center, some pre-analysis changes were made to achieve an analysis that better reflects the country’s reality. Since for some NUTS III it was not possible to characterize a given hospital individually, the data from that hospital was presented together with hospitals from another NUTS III. Therefore, NUTS III 11D and 11B (Douro and Alto Tâmega) were analyzed as one (11BD). NUTS III 16B and 16F were also aggregated (Oeste and Região de Leiria) and formed a new NUTS III analyzed as 16BF. The population estimates for each region were used, and the populations of the two groups were combined to calculate the population of the new group. There is also a particular case between NUT III, 11A (Metropolitan Area of Porto) and 119 (Ave), where the data from the hospital center of a municipality in Ave (0312- Vila Nova de Famalicão) is presented together with a hospital in the Metropolitan Area of Porto. Since there is no way of distinguishing between the two hospitals, the data has been counted in 11A. In relation to the population of these two NUTS, the population of the municipality of Vila Nova de Famalicão was removed from 119 and added into the population of 11A.

Human resources study

The first analysis of hospitals is based on the group of variables related to Human Resources of Portuguese Hospitals in the NHS. There were initially 12 variables (Doctors – Specialists, Doctors - Non-specialists, Doctors – in training, Nurses – Specialists, Nurses - General Care, Other staff - Senior Health Technicians, Other staff - Senior Technicians, Other staff - Diagnostic and/or Therapeutic Technicians, Other staff - Administrative Assistants, Other staff - Operational Assistants, Other Staff - Management Staff, Other staff – Others) for this observation topic. The population estimates for each NUT III in 2019 were used.³³

This analysis was carried out to obtain a general perception of the level of human resources per 1000 inhabitants in the different NUTS III. Subsequently, twelve new variables were created that showed the number of specialists doctors per one thousand inhabitants.

The variable “Other Staff - Management Staff” was removed, as it is stated in the survey that ‘if a manager carries out another type of activity in the hospital, they should only be included in the question relating to that other activity’, so the number shown in the database does not represent the actual number of managers.

The variable “Other staff – Others” was also removed. Since is not possible to know what type of human resources is being accounted for, there is a risk of conducting an unfair analysis.

For the variable Doctors Non-specialists, only two NUTS had values different than zero, so this type of human resources was also excluded from the analysis.

The Min-Max method was used to standardize the data, and the dissimilarity matrix was then calculated using the Euclidean distance. An ascending hierarchical cluster analysis was carried out using the Ward aggregation method, represented in the following dendrogram (Figure 3).

Figure 3 Dendrogram using Ward´s Method with three clusters.

An initial analysis shows the formation of three clusters, each identified by a different color in the following dendrogram (Figure 4).

Figure 4 Dendrogram using Ward´s Method with seven clusters (Without Coimbra).

We can see two big clusters and NUT III 16E (Coimbra), which is isolated in its own cluster. This NUT III has the highest values for Portugal for seven of the nine variables, excluding only the Senior Health technicians and Senior Technicians variables. Repeating the cluster analysis without “Coimbra Region” -we got the dendrogram present on (Figure 5).

Figure 5 "Elbow" method.

Starting with a refined analysis of the dendrogram, it is possible to see the existence of 7 intermediate clusters (Figure 6).

Figure 6 Silhouette method.

Starting the interpretation from left to right, it’s possible to see a cluster, with two NUTS III {16I,181} (Médio Tejo, Alentejo Litoral). This cluster shows significant deficiencies in terms of specialist doctors, doctors in training, and specialized nurses. The Alentejo Litoral region has the lowest values in the country for both doctor-related variables. Additionally, it underperforms compared to Médio Tejo in terms of general care nurses, senior health technicians, and operational assistants.

Next, there is compassing five regions {11C, 16D, 16BF, 119,185} (Tâmega e Sousa, Região de Aveiro, Oeste e Região de Leiria, Ave, Lezíria do Tejo). Excluding the variable of specialist doctors, this cluster is characterized by very low values for all the variables, containing the minimum values among seven out of the nine variables in the country.

The third cluster with NUTS III {11A and 170} - Metropolitan Area of Porto and Metropolitan Area of Lisbon. These two regions rank in the top two nationwide (without Coimbra) in terms of both the number of specialized doctors and the number of doctors in training, with Porto Metropolitan area slightly surpassing the other. Concerning the number of Specialized Nurses, there is a discrepancy between these two regions. The Porto Region ranks second in the country in this variable, while Lisboa metropolitan area clearly lacks in this aspect. The Lisbon area stands out slightly in terms of the number of general care nurses and Senior Health Technicians. This cluster still has room for improvement in the number of senior technicians compared to the best regions of the country in this variable.

In fourth cluster, there are six regions {111,112,11BD, 187,150,16G} - Alto Minho, Cávado, Douro e Alto Tâmega, Alentejo Central, Algarve, Viseu Dão Lafões. This cluster has intermediate values for Portugal. It has better values than Clusters 1 and 2 in most of the variables, but they are also not reference values for the country. However, it shows poorer performance in terms of the number of senior technicians. Regions Cávado and Viseu Dão Lafões stand out positively in terms of the number of specialized doctors and Doctors in training.

In fifth cluster, there are two regions {11E,16J} - Terras de Trás-os-Montes, Beiras e Serra da Estrela. This cluster performs well in almost all variables, though it has deficiencies in specialist doctors and senior health technicians. The Region of Terras de Trás-os-Montes has the highest relative number of specialized nurses in the country.

In sixth cluster, there are 3 NUTS III {16H,186,184} - Beira Baixa, Alto Alentejo, Baixo Alentejo. This cluster ranks well in almost all variables, except for the number of specialized doctors and doctors in training, where it stands out negatively. Beira Baixa region has an intermediate score for the number of specialized doctors, while the other two regions are in the bottom five nationwide for this variable. NUT III Beira Baixa also stands out in terms of the number of nurses in general care and Senior Health technicians.

The last cluster includes two NUTS {200,300} - Região Autónoma dos Açores, Região Autónoma da Madeira. They stand out negatively in terms of doctors in training. While Madeira appeared in the top three of the country for the variables Specialized nurses and Senior Health technicians, the Açores showed some deficiencies. This cluster stands out positively in terms of General care nurses, Senior Technicians, Diagnostic and/or Therapeutic Technicians, Administrative Assistants and Operational Assistants. Açores is the region with the highest value in the country for these five variables mentioned before.

Next, a non-hierarchical cluster analysis, k-means, was carried out.

By analyzing the “elbow” method (Figure 7) and the Silhouette method (Figure 8), the number of clusters chosen was five.

Figure 7 kmeans results with five clusters.

Figure 8 Regional distribution of clusters in Portugal´s map.

Then the k-means approach was used with 5 clusters, getting the following results (Figure 9 and Table 3).

Figure 9 Surgical performance dendrogram using the single linkage method.

In fact, the two first principal axes explain about 84% of total inertia. The first axe is a size
factor and the second axe explain the differentiation of NUTS III in that concerns the number of specialized doctors or doctors in training per 1000 inhabitants.

Table 4 provides a detailed breakdown of the relative contribution of each variable to the total variability between clusters. These values highlight which groups of healthcare professionals contribute most significantly to the overall variability between clusters, thereby indicating their influence on the clustering results.

The table shows a consistent level of stability in the percentage of contributions of the variables to the total variability between clusters. Most variables contribute in a similar manner, suggesting that these variables have similar levels of influence in the analysis.

There is only one exception, the variable of Senior Health Technicians, which indicates a lower capacity to differentiate the clusters.

By analyzing the total variability within each cluster (Table 5), we can understand which cluster is more homogeneous and which exhibits greater internal heterogeneity and table 6 explain the relative contribution of each variable to such variability per cluster.

Cluster 3 is the most homogeneous, followed by clusters 4 and 6. On the other hand, clusters 2 and 5 are the most heterogeneous.

Starting with Cluster 3, the most homogeneous cluster which includes the metropolitan areas of Porto and Lisbon. Almost 70% of the internal variability is explained by the variable Specialized Nurses. In this variable, Porto is ranked as the second-best region in the country, while Lisbon shows deficiencies. This cluster is characterized by the best values in the country for Specialist doctors and Doctors in training. For the remaining categories, the cluster's average is always above the median of each variable.

Next is Cluster 4, where the variables Specialist Doctors, Specialist Nurses, and Administrative Assistants explain 65% of the variability within. Regarding the variable Specialist Doctors, the Beira Baixa region stands out positively, while the other regions show evident deficiencies. In terms of the number of Specialist Nurses and Administrative Assistants, the Médio Tejo region has much lower values compared to the others. This cluster is characterized by deficiencies in Doctors in Training and has intermediate values for the country in Diagnostic and/or Therapeutic Technicians. It stands out positively in the number of Senior Technicians.

The following is Cluster 6, with its internal variability explained by almost 65% by the variables Doctors in Training, General Care Nurses, and Diagnostic and/or Therapeutic Technicians. For Doctors in Training, regions Ave and Lezíria do Tejo stand out positively. Regarding the variable General Care Nurses, there is significant heterogeneity, even though this cluster includes the NUTS with the six lowest values in the country. This heterogeneity is explained by the very low values in regions Tâmega e Sousa, Aveiro region, and Oeste and Região de Leiria, showing evident lack of resources. For the number of Diagnostic and/or Therapeutic Technicians, regions Alentejo Litoral and Lezíria do Tejo show superior values. This cluster is generally characterized by deficiencies in all variables, with some NUTS standing out either positively or negatively, even when compared to the other worst-performing regions in specific variables as explained earlier.

Cluster 5 is one of the clusters with the highest heterogeneity. The variables Doctors - In training, Nurses – Specialists and Diagnostic and/or Therapeutic Technicians account for 70% of the variability within, with the latter two being the most prominent. Starting with the Specialized nurses, the NUTS Alentejo Central and Alto Tâmega e Douro show superior values than the others. Regarding the number of Diagnostic and/or Therapeutic Technicians per 1000 inhabitants, Alto Minho and Cávado stand out negatively from the other regions in this cluster. For the variable Doctors - In training, Viseu and Cávado are outstanding. In the category specialized doctors Algarve and Alto Minho stand out negatively. This cluster is characterized by good national rankings in the variables related to doctors, but for the remaining categories, it shows lower average values compared to the previously analyzed clusters, excluding cluster 6.

Finally, we have Cluster 2, which presents the highest internal variability, explained 70% by the variables Specialist Nurses, Senior Health Technicians, Senior Technicians, and Operational Assistants. The variable with the greatest prominence is Senior Health Technicians, where Madeira is outstanding with the highest value in the country. For the variable Specialist Nurses, the Azores show a lack of resources, while the other regions in the cluster are in the top four nationwide. For the remaining two variables that most explain this variability, these four regions are the top four in the country. However, for the variable Senior Technicians, the disparity between the first place (Azores) and the fourth (Terras de Trás-os-Montes) is significant. For the variable Operational Assistants, the Azores and Madeira stand out from the rest of the country.

In conclusion, clusters 6 and 5 require greater attention and reinforcement overall. However, the remaining clusters exhibit specific deficiencies that are easily noticeable through the methods used and the analysis of total variabilities. This analysis clearly demonstrates the deficiencies of each cluster and the respective regions in the year 2019, identifying what each region needs to improve its performance in terms of human resources per 1000 inhabitants.

The cartogram (figure 9) illustrates the geographical distribution of clusters in Portugal, based on the performance of human resource factors in Public Hospitals for the year 2019. This map represents disparities in the distribution of healthcare resources, facilitating the identification of places with notable strengths and weaknesses in terms of human resources.

There is a significant continuity of regions along the coast in Cluster 6, stretching from the Região de Leiria, Oeste, Lezíria do Tejo, and Alentejo Litoral. These areas show significant deficiencies in all human resource variables. If MR of Lisboa and Algarve are added to this group along the coast, it’s possible to see from Leiria to Algarve a clear deficit in specialized nurses, for the year 2019.

The Metropolitan Area of Porto is surrounded by red, or orange regions where most of them had a lack of general care nurses.

The Coimbra and Beiras e Serra da Estrela regions exhibit exceptional performance, showing relatively strong human resource indicators in this central area.

A yellow zone representing the NUTS regions in Cluster 4 is present in the Centre and Alentejo. This area encopasses the regions surrounding Alentejo, namely Médio Tejo, Beira Baixa, Baixo Alentejo, Lezíria do Tejo, Alto Alentejo, and Alentejo Litoral. All these regions had a low number of specialized doctors per 1,000 inhabitants in 2019. In that area, only Alentejo Central had a high concentration of specialized doctors. The Algarve also appears poorly classified in this variable, indicating a deficiency in specialized doctors in this continuous area of the country.

These insights emphasize the necessity of implementing specific healthcare strategies and allocating resources to successfully address the identified deficiencies. By focusing efforts on the regions with the greatest weaknesses, policymakers can work towards achieving a more balanced and equitable distribution of healthcare resources across Portugal.

Surgical specialities evaluation

The second indicator intended for study was the number of surgeries in each specialty per the number of doctors in that same specialty for each of the NUTS III regions; however, this analysis encountered some difficulties. There were 13 surgical specialties in the database. Therefore 26 variables were selected (the number of doctors in the thirteen specialties; the number of surgeries in the thirteen specialties). It is important to highlight that in response to the question regarding the number of specialist doctors in each specialty, the response instructions indicated that doctors should be counted only once. Meaning that in cases where a doctor practiced in more than one specialty, they should only be counted in the one where they worked the most hours. This limitation raised two problems. Firstly, the number of doctors in each specialty may be under-represented in certain regions. Secondly, this led to missing values. Some regions that did not report having doctors in a certain specialty still recorded surgeries in that same area. This could be due to several reasons, such as the temporary relocation of a medical team from one region to another to perform certain surgeries, which is common, for example, in the Autonomous Regions of Madeira and the Azores, but not exclusively. The possibility of a doctor having more than one specialty could also be a factor behind missing values. As it is impossible to distinguish whether this is indeed a missing value or simply a null value, and to avoid the risk of an erroneous analysis, it was decided to analyze only the number of surgeries in each specialty in each NUT III.

To understand the surgical dynamics in Portugal in 2019, 13 variables were chosen, each representing the number of surgeries performed in a particular specialty during that year. The variables are Angiology and Vascular Surgery, Cardiothoracic Surgery, General Surgery, Maxillofacial Surgery, Pediatric Surgery, Plastic, Reconstructive and Aesthetic Surgery, Stomatology, Gynecology-Obstetrics, Neurosurgery, Ophthalmology, Orthopedics, Otorhinolaryngology, and Urology. Both urgent and scheduled surgeries were counted.

Next, converting some of these variables into binary reduces the issue of having many zeros and makes the data easier to understand and work with. So, all the variables that had more than half of the NUTS III with null values were transformed into binary variables. "Yes", if there were surgeries of this specialty in 2019 in the region in question; "No", if there were no surgeries of this specialty in the same year in that region. The variables Cardiothoracic Surgery, Maxillofacial Surgery, Pediatric Surgery and Neurosurgery were then converted. Since a region having services in a certain specialty is rarer and yet more important, the binary variables were considered as asymmetric binary variables.

Explaining the information on this variable before they were converted, it’s possible to note that, regarding Cardiothoracic Surgery, 97.7% of surgeries in this specialty in 2019 took place in the Porto Metropolitan Area, Lisbon Metropolitan Area and Coimbra region. In relation to Pediatric Surgery and Neurosurgery, almost 90% of the surgeries in the country, in both specialties were performed in Porto, Lisbon, Coimbra, and Cávado. In terms of Maxillofacial Surgery, the Viseu region ranks as the fourth, and together with Porto, Lisbon, and Coimbra, represents 89% of the surgeries performed in this field.

Subsequently, an analysis of the variables with mixed data was conducted, including 4 asymmetric binary variables and 9 numerical variables. The dissimilarity matrix was calculated using Gower's formula, and then the Single Linkage aggregation method was applied, resulting in the following dendrogram (Figure 10). This method was chosen over the Complete Linkage and Average Linkage methods, since a chain effect is expected.

Figure 10 Surgical analysis dendrogram using the single linkage method with three clusters.

There are three main clusters, which are represented by different colors. The choice of colors was determined by the surgical volume. The first cluster, which includes the two metropolitan areas, showed the highest surgical volume and was therefore assigned the dark blue. The cluster with the lowest number of surgical specialties was assigned to the color red. The remaining cluster was colored grey, as it represents an intermediate cluster.

Starting with the analysis of the main clusters, the blue cluster is composed of the NUTS III regions 11A and 170, corresponding to the Porto Metropolitan Area and the Lisbon Metropolitan Area, respectively. These two regions stand out due to their high volumes of surgeries across all areas. In 2019, surgeries were performed in all thirteen surgical specialties in these regions. The isolation of this cluster from the others was expected and is justifiable, as these are two major urban centers that need to respond to a vast and varied number of requests from the population.

The red cluster is composed by thirteen NUTS III regions: 11BD (Alto Tâmega e Douro), 11C (Tâmega e Sousa), 16BF (Oeste e Região de Leiria), 16I (Médio Tejo), 11E (Terras de Trás-os-Montes), 185 (Lezíria do Tejo), 16H (Beira Baixa), 186 (Alto Alentejo), 181 (Alentejo Litoral), 184 (Baixo Alentejo), 119 (Ave), 16J (Beiras e Serra da Estrela), 111 (Alto Minho), and 16D (Região de Aveiro). The regions in this group didn´t have surgeries in the areas of Cardiothoracic Surgery, Pediatric Surgery and Neurosurgery.

Initially, two chains can be observed in this cluster. The first chain begins with regions 186 (Alto Alentejo), 181 (Alentejo Litoral) and 184 (Baixo Alentejo). Beside the three surgical specialties that none of the regions in this cluster offer, these three NUTS do not have any specialties in Angiology and Vascular Surgery, Maxillofacial Surgery, Plastic, Reconstructive and Aesthetic Surgery, Stomatology.

The next region to be added to the chain is 16H (Beira Baixa). In terms of surgical specialties, it maintains all those present in the previous NUTS and adds Stomatology. The volume of surgeries for each specialty is similar, differing only in the Otorhinolaryngology specialty, where it is higher.

The following areas are 11E (Terras de Trás-os-Montes), 185 (Lezíria do Tejo). The Terras de Trás-os-Montes region maintains the specialties available in Beira Baixa, differing only in the higher number of Orthopedic surgeries. Lezíria do Tejo has no capacity in Stomatology but adds the Angiology and Vascular Surgery specialty. This NUT, compared to the others mentioned above, has a higher number of surgeries in Gynecology-Obstetrics.

The last region in this sequence is 16I (Médio Tejo). In terms of specialties, it has neither stomatology nor angiology nor vascular surgery, so it has this in common with the first three NUTS in this chain. However, it has higher values in General Surgery, Ophthalmology and Urology when compared to the other regions in this chain.

The second chain begins with NUTS 111 (Alto Minho), 16D (Região de Aveiro). Compared to the three initial regions of the first chain, Alto Minho and Região de Aveiro have resources in Stomatology. The surgical numbers for these two areas are higher, in all specialties, than the NUTSs present in the first chain.

Regions 119 (Ave) and 16J (Beiras e Serra da Estrela) complete this second chain. In terms of available specialities, the Beiras e Serra da Estrela region is identical to the first two NUTS regions in this chain. It stands out only in the number of Stomatology surgeries, having the highest value in Portugal, surpassed only by the Lisbon Metropolitan Area and the Porto Metropolitan Area. The Ave NUTS does not include Stomatology among its specialties but distinguishes itself from the others by offering Angiology and Vascular Surgery, and Plastic, Reconstructive and Aesthetic Surgery.

Next, it is visible in the dendrogram that these two chains merge, forming the base of a new one. The first region to be added is 16BF (Oeste e Região de Leiria). Despite having the same areas of expertise as Alto Alentejo, Alentejo Litoral, and Baixo Alentejo, it shows much higher values in General Surgery, Ophthalmology, Orthopedics, and Gynecology-Obstetrics compared to the NUTS present in the two chains. As mentioned above, it's important to emphasize that these values are aggregates from the two regions of Oeste and Leiria Region.

The following NUT added to this chain is 11C (Tâmega e Sousa). It offers additionally the specialties of Angiology and Vascular Surgery, Plastic, Reconstructive and Aesthetic Surgery, and Stomatology. It also stands out for its higher values in General Surgery, Gynecology-Obstetrics, Ophthalmology, and Orthopedics. Also noteworthy is the surgical specialty of Angiology and Vascular Surgery. This region has the highest number of surgeries in the country, second only to the two metropolitan regions.

To complete this chain and cluster, only NUT 11BD (Alto Tâmega e Douro) is missing. Compared to Tâmega e Sousa, this region doesn't have stomatology services nor such higher figures for other surgical specialties. However, Alto Tâmega e Douro is highlighted for being the only one in this cluster with maxillofacial surgery competencies.

To conclude this analysis of the 3 main clusters, only the grey cluster remains to be examined. It is composed by seven regions: 16E (Região de Coimbra), 112 (Cávado), 16G (Viseu Dão Lafões), 150 (Algarve), 187 (Alentejo Central), 200 (Região Autónoma dos Açores), and 300 (Região Autónoma da Madeira).

In this cluster it is also possible to identify the existence of a chain. At the base are the NUTS 200 (Região Autónoma dos Açores) and NUT 300 (Região Autónoma da Madeira). These two regions differ only in the variable of Maxillofacial Surgery, where Madeira did not record any surgeries in this area. Regarding the remaining variables, both regions have the same surgical specialties: Angiology and Vascular Surgery, Cardiothoracic Surgery, General Surgery, Pediatric Surgery, Plastic, Reconstructive and Aesthetic Surgery, Stomatology, Gynecology-Obstetrics, Neurosurgery, Ophthalmology, Orthopedics, Otorhinolaryngology, and Urology. It should be noted that the Azores had all areas of expertise.

Next in the chain are the regions 150 (Algarve) and 187 (Alentejo Central). These two regions have the same specialties as Madeira, except for Cardiothoracic Surgery, where no surgeries were performed. These two NUTS differ only in the Angiology and Vascular Surgery variable, where the Algarve had no surgery in this area. Regarding surgical volume, compared to the two regions at the bottom of the chain, the Algarve stands out in the number of Gynecology-Obstetrics surgeries, while Alentejo Central has higher volumes in Plastic, Reconstructive and Aesthetic Surgery and Ophthalmology.

The next line in the sequence is the pair made up of NUTS 112 (Cávado), 16G (Viseu Dão Lafões). Compared to the Azores, these two regions no longer perform Cardiothoracic Surgeries. The Viseu region also differs by not having any Stomatology surgeries. It is important to highlight Cávado, as it ranks in the top 5 in the country in terms of surgical volume, except for General Surgery.

Finally, we have NUT 16E (Região de Coimbra). Coimbra is like the Azores as it also offers all surgical specialties. It should be noted that Coimbra is the region in the country with the highest surgical volume, outside the Metropolitan Areas, in six of the nine numerical variables (General Surgery, Gynecology-Obstetrics, Ophthalmology, Orthopedics, Otorhinolaryngology, Urology). In the remaining variables, it consistently ranks in the Top 5 in Portugal. Proving to be a very important medical center in the Country.

The differences between these two clusters are clear. The grey cluster includes NUTs with a wider surgical range, i.e. regions where a greater number of surgical specialties were performed.

Then non-hierarchical methods were applied. As there were some binary variables in the data set, the K-means couldn´t be executed. The approach chosen was the k-medoids.

By the analysis of the Silhouette approach (Figure 11), the number of clusters chosen was three.

Figure 11 2nd analysis Silhouette method.

Then the k-method approach was used with 3 clusters, getting the following results. (Table 7 and Figure 11).

This method produced identical results with the hierarchical one, with the same arrangement of clusters obtain. This alignment confirms the consistency and reliability of the clustering results.

The cartogram (figure 12) highlights the regional disparities in surgical services across Portugal, with each cluster demonstrating distinct characteristics in terms of surgical specialities and volumes.

Figure 12 2nd analysis - k-medoids results with three clusters.

Figure 13 2nd analysis regional distribution of clusters in Portugal´s map.

The blue cluster indicates the presence of advanced surgical services in major urban centres like Porto and Lisbon. The grey cluster represents areas that have a diversified selection of surgical specialties and moderate surgical volume. The red cluster highlights the difficulties faced by rural and peripheral areas in accessing healthcare.

Both the blue and grey clusters incorporate essential healthcare centres that provide vital support for local and neighbouring populations in specific surgical procedures. The two first principal axes explain 97.4% of total inertia. The first principal axe is a size factor making in evidence the strongest surgical capacity of metropolitan areas and the second principal axe express a “Gutman effect” opposing the intermediate clusters to the extremes clusters.

Despite most of the country being coloured red, indicating limited surgical capacity, a closer examination of the NUTS II regions shows that there is at least one area in the blue or grey cluster providing support to the other regions within each NUTS II. For example, In the Northern region, the Porto Metropolitan Area and Cávado are notable for their larger and more varied surgical volumes, providing important assistance to the rest of the region. Coimbra and Viseu are crucial in the Central Region as they support this region with significant surgical capacities. In Alentejo, Alentejo Central is notable for its surgical volume, providing crucial support to the surrounding areas. Additionally, the Algarve and the archipelagos (Azores and Madeira) support their municipalities within their regions.

Patient mobility is an important factor to consider. These clusters do not represent physical boundaries, and it is quite common for patients to travel from rural and peripheral regions to urban centres inside the blue and grey clusters for surgical procedures. This movement emphasizes the importance of strategically locating specialized centres to ensure they are accessible to a wider population.

We would like to thank the Instituto Nacional de Estatística (INE) and the Direção-Geral de Estatísticas da Educação e Ciência (DGEEC) for providing access to the official anonymized statistical data used in this study. This access was granted following the established accreditation process, as outlined in the Cooperation Protocol between INE, DGEEC, and the Fundação para a Ciência e a Tecnologia (FCT, I.P.), which ensures the confidentiality and ethical use of the data for scientific research purposes. Their support was essential to the development of this research.

None.

There are no conflicts of interest for the authors.

1. Pineault R. Compreendendo o sistema de saúde para uma melhor gestão. LEIAAS. 2016;2(1):.
2. Popescu ME, Militaru E, Cristescu A et al. Investigating health systems in the European Union: outcomes and fiscal sustainability, 2018.
3. Daniels N. Just health: meeting health needs fairly. Cambridge University Press. 2008.
4. Folland S, Goodman AC, Stano M. The economics of health and health Care. Pearson new international edition. The economics of health and health care. 2016.
5. Gostin LO, & Powers M. What does social justice require for the public’s health? Public health ethics and policy imperatives. Health affairs.2006: 25(4).
6. Uchmanowicz I, Lisiak M, Wleklik M, et al (2024). The impact of rationing nursing care on patient safety: A systematic review. Med Scie Monitor. 2024.
7. Woolf S, Jonas S, Kaplan-Liss E. Promoción de la salud y prevención de enfermedades en la práctica clínica. 2008.
8. OECD. Health at a glance 2021: OECD Indicators. OECD. 2021: 274.
9. Yamada T. Global perspectives of different healthcare systems and health: Income, education, health disparity, health behaviors and public health in China, Japan and USA. Community Med Public Health Care. 2018.
10. Khan S, Saied I M, Ratnarajah T, Arslan T. Evaluation of unobtrusive microwave sensors in healthcare 4.0—toward the creation of digital-twin model. 2022.
11.  Low LL, Yan S, Kwan YH, et al. Assessing the validity of a data driven segmentation approach: a 4 year longitudinal study of healthcare utilization and mortality. PLoS One. 2018;13(4):e0195243.
12. INE. Estimativas da População Residente em 2023. 2024.
13. Barros PP. Health policy reform in tough times: The case of Portugal. Health Policy. 2012.
14. INE. As novas unidades territoriais para fins estatísticos. 2015.
15. Alaaraj H, Aoun M. Financial performance indicators in lebanese hospitals: a sustainable improvement strategy. J Acco Fin Emer Eco. 2016;2(2):69–75.
16. Motkuri V, Mishra US. Human resources in healthcare and health outcomes in India. Millennial Asia. 2020;11(2):133–159.
17. Buggy CJ, Ashworth HC, Roux TL, et al. Physical barriers and attitudes towards accessing healthcare in a rural Muslim population in Nepal. Asian Pac. J. Health Sci. 2020;7(1):7–12.
18. Carvalho P, Souza J, Botelho F, et al. Multimorbidity patterns among patients hospitalized with prostate cancer in Portugal: a cluster analysis approach. Instituto Superior de Engenharia Do Porto. 2024.
19. Makalesi A, Yalçin Balçik P, Demirci Ş, et al. Comparison of European countries’ health indicators and health expenditures by clustering analysis. Academic Rev Econ Adminis Sci. 2021;14(2):365–377.
20. Mars N, Kerola AM, Kauppi MJ, et al. Cluster analysis identifies unmet healthcare needs among patients with rheumatoid arthritis. Scan J Rheu. 2022;51(5):355–362.
21. Pinheiro Junior RVB, Junior NC, Sala A, et al. Primary health care performance according to clusters of convergent municipalities in the state of São Paulo. Revista Brasileira de Epidemiologia. 2022.
22. Wendt C. Mapping European healthcare systems: a comparative analysis of financing, service provision and access to healthcare.Millennial Asia. 2009;19(5):432–445.
23. Hair JF , Black W C, Babin BJ, et al.Multivariate Data Analysis. 2010.
24. Estabrook GF, Rogers DJ. A general method of taxonomic description for a computed similarity measure. BioScience.1966;16(11):789–793.
25. Lerman IC. Construction of a similarity index between objects described by variables of any type. Application to the problem of consensus in classification. J Appl Statistics.1987;35(2):39–60.
26. Gower JC. A general coefficient of similarity and some of its properties. Biometrics.1971;27(4):857–874.
27. Everitt BS, Landau S, Leese M. Cluster analysis. Cluster Analysis. 5th Edition.2011;1–330.
28. Gordon AD. Hierarchical classification. World Scientific. 1996.
29. MacQueen J. Some methods for classification and analysis of multivariate observations.1967;281–298.
30. Rousseeuw PJ. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J Comput Appl Math. 1987;20(C):53–65.
31. Kaufman L, Rousseeuw PJ. Finding Groups in Data. 1990.
32. Diday E. The dynamic clusters method in nonhierarchical clustering. Int J Compu Inform Sci. 1973;2(1);61–88.
33. PORDATA. Onde há mais e menos pessoas? 2019.