The urgency of preventing serious mental disorders (MDs) has intensified in recent decades demanding innovative approaches for early diagnosis. This paper’s main objective is to revisit statistical discriminant methods emphasizing their crucial and practical role to classify patients into different MDs categories. From three groups (nervous, psychotic, and healthy) of fifty individuals, each evaluated by thirty variables, an exploratory discriminant analysis was performed in order to obtain the linear combination of the variables who maximize the separation between these groups. From the statistical analysis of the two first discriminant functions, it was identified a subset of fifteen variables which discriminant power revealed a misclassification rate of 10% in the training test and 14.6% in the testing test. Finally, this model was compared to a discriminant stepwise method which identified eighteen discriminant variables.

At the Era of Artificial Intelligence, it makes sense to provide National Health Systems with automatic tools which may effectively help Physicians to get an early diagnose of mental disorders diseases.

Keywords: mental disorders, principal component analysis, factorial discriminant analysis, stepwise discriminant analysis

DA, discriminant analysis; DF, discriminant function; FDA, factorial discriminant analysis; TND, truncated normal distribution; VIF, variance inflation factors

Mental disorders (MDs) are conditions that can disrupt a person's behavior, well-being, and emotional state. When left untreated or misdiagnosed, they can have tragic consequences, including self-harm and suicide. Research has shown that people with mental health issues have a higher mortality rate compared to those who have not.^1,2

MDs include anxiety disorders (ADs), post-traumatic stress disorder, disruptive behavior disorders, bipolar disorder, dissocial disorders, depression, schizophrenia, neurodevelopmental disorders, and eating disorders. Research suggests that ADs are particularly common, with estimates of their global prevalence ranging from 3.8% to 25%.³

People with ADs may experience panic attacks, changes in appetite, sweats, and palpitations, among other symptoms.⁴ According to,⁵ individuals with anxiety are 26% more susceptible to the risk of developing coronary heart disease and almost 50% more susceptible to the risk of cardiac death.

Accurate and early diagnosis of MDs is crucial for effective treatment and can help prevent people from experiencing more severe states of mind. However, diagnosing them can be challenging, and misdiagnosis can lead to inappropriate treatment and continued suffering.⁶

This paper aims to use Factorial Discriminant Analysis (FDA) to develop rules for classifying new individuals into one of three categories: nervous, psychotic, or healthy,

• Identifying the variables that best discriminate the three classes under study;
• Identify the number of discriminant functions needed to represent the differences among the groups;
• Creating a rule to classify future observations into one of the three groups and develop a misclassification apparent rate matrix.

This paper will be supported by a study conducted by Professor P. Pichot at the Saint-Anne Hospital. The study involved a survey of thirty questions, evaluating thirty distinct characteristics enumerated in Table 1. In such study, each question was rated on a continuous scale from zero to four based on the frequency and intensity of symptoms in the days before the examination. It was known beforehand that out of a hundred and fifty young adults, fifty were classified as nervous, fifty were classified as psychotic, and fifty were classified as not having any mental health condition – therefore classified as healthy. Forty individuals from each group were selected for the training sample and were assigned to groups one, two, and three. The remaining ten observations from each group were selected to take part in a testing sample.

Out of the hundred and twenty questionnaires, the answers from each participant in the training sample were displayed in two separate tables, showing the mean of each variable for each group, and the standard deviation of each variable and for each group as shown in Tables 2 & 3, respectively.

In this study, and due to the need of having every individual result from each participant to perform a discriminant analysis technique, a Monte Carlo simulation was made of a hundred and fifty participants, fifty for each group. The data was generated recurring to the truncated normal distribution (TND) recurring to the mean values in Table 2 and the standard deviation values in Table 3.

Supposing that $X$ has a TND with mean $\mu$ , standard deviation $\sigma$ , inferiorly truncated by "$a$ " and superiorly truncated by "$b$ ", its density function is given by

$f\left(x\right)=\frac{\frac{1}{\sigma \sqrt{2\pi }}{e}^{\frac{-{(x-\mu )}^2}{2{\sigma }^2}}}{\Phi \left(\frac{b-\mu }{\sigma }\right)-\Phi \left(\frac{a-\mu }{\sigma }\right) }, a\le x\le b$   2.1

where $\Phi$ is the standard normal distribution cumulative distribution function, which is defined by

$\Phi \left(x\right)=\frac{1}{\sqrt{2\pi }}\underset{-\infty }{\overset{x}{{\displaystyle \int }}}{e}^{\frac{-t^2}{2}}dt.$   2.2

Statistical analysis

Factorial discriminant analysis: Let $X$ be the table with the p quantitative variables, and $A$ a logic table associated with a qualitative variable with $r=3$  modalities. Let $p_i$ be the weight attributed to each individual $i$ , and let

$P_r={\displaystyle \sum }_{i\in C_r}{p}_i$   2.3

be the weight of class $C_r$  and

$g= {\displaystyle \sum }_{i=1}^n{p}_i{x}_i$   2.4

the center of gravity of the total cluster. As a result,

$g_r=\frac{1}{p_r}{\displaystyle \sum }_{i\in C_r}{p}_i{x}_i$   2.5

will be the center of gravity associated with the class $C_r$ and $g$ can also be calculated as

$g= {\displaystyle \sum }_{k=1}^3{P}_k{g}_k.$   2.6

The Variance and Covariance matrix is defined by

$V={}_{ }{}^{t}XDX= {\displaystyle \sum }_{i=1}^n{p}_i(x_i-g){*}^t\left(x_i-g\right)$   2.7

where $D$ is the matrix of the weights attributed to the individuals. The variance between groups ($B$ ) measures the variability between the means of each group under study, quantifying how much each group differs from one another, while the variance within groups ($W$ ) measures the variability of individuals within each group. The variance between groups can be calculated by

$B={\displaystyle \sum }_{k=1}^3{P}_k(g_k-g){*}^t\left(g_k-g\right)$   2.8

while the variance within groups can be calculated by

$W={\displaystyle \sum }_{k=1}^r{\displaystyle \sum }_{i\in C_r}{p}_i(x_i-g_k){*}^t\left(x_i-g_k\right).$   2.9

It can be shown that the sum of both between variance and within variance represents the total variability of the data, previously referred to as $V$ .

To reach this paper’s main purpose, one of the settled objectives is to obtain the linear combination of the thirty variables under study that best discriminates the classes. Being $\propto$  the vector of the coefficients associated with each independent variable, then $C$ can be represented as the linear combination

$C={\displaystyle \sum }_{j=1}^p{\propto }^j{x}^j$   2.10

which will be used to maximize the variance between groups. The respective variance can be calculated by

$s^2\left(C\right)=|\left|C\right|{|}_D^2={}_{ }{}^{t}CDC$   2.11

and by equivalence, is equal to ${}_{ }{}^t\propto V\propto$ , demonstrated in.⁷ As the total variance,$V$ , can be decomposed into the within-group variance, $W$ , and between-group variance, $B$ , then

${}_{ }{}^t\propto V\propto = {}_{ }{}^t\propto W\propto +{}_{ }{}^t\propto B\propto$   2.12

and so

$s^2\left(C\right)={}_{ }{}^t\propto W\propto +{}_{ }{}^t\propto B\propto .$   2.13

To obtain the linear combination $C$ that best discriminates the classes, the optimal solution will be the vector $\propto$  under the condition $x \frac{{}_{ }{}^t\propto B\propto }{{}_{ }{}^t\propto V\propto }$ , where ${}_{ }{}^t\propto V\propto$  is constant.

Without loss of generality, it is considered ${}_{ }{}^t\propto V\propto =1$ , simplifying the optimal solution to maximizing ${}_{ }{}^t\propto B\propto$ . The maximum is obtained when the vector $\propto$  is the eigenvector of $V^{-1}B$ associated with the highest eigenvalue ${\lambda }_1$ :

$V^{-1}B\propto ={\lambda }_1\propto$   2.14

so $\frac{{}_{ }{}^t\propto B\propto }{{}_{ }{}^t\propto V\propto } = {\lambda }_1$ . As a result, the highest eigenvalue ${\lambda }_1$ will measure the discriminant power associated with the first discriminant function

$C_1={\displaystyle \sum }_{j=1}^p{\propto }^j{x}^j$   2.15

where ${\propto }^j$  are the coordinates of the eigenvector $\propto$ . To test the significance of each DF, the likelihood ratio test will be performed to determine whether or not the DF under analysis is relevant to discriminate the individuals.

Like maximizing $\frac{{}_{ }{}^t\propto B\propto }{{}_{ }{}^t\propto V\propto }$ , the maximization of $\frac{{}_{ }{}^t\propto B\propto }{{}_{ }{}^t\propto W\propto }$  will produce equivalent results. Its solution will be the eigenvector of $W^{-1}B$ associated with the highest eigenvalue

$W^{-1}B\propto ={\gamma }_1\propto .$   2.16

The eigenvector will remain the same, but the eigenvalue will be

$\gamma =\frac{\lambda }{1-\lambda }, \lambda <1$   2.17

The new metric will be $W^{-1}$  as in opposition to the previous metric $V^{-1}$ , the metric of Mahalanobis.

There can be at most $r-1$ DFs, being $r$ the number of classes under study. In the most complex problems, to separate $r$  groups from each other, $r-1$  boundaries will be generally needed.

Supposing that a new observation, $x_0$ , is obtained, the objective will be to allocate the observation to the nearest group recurring to the Mahalanobis distance (with metric $W^{-1}$  or the equivalent metric $V^{-1}$ ) calculated by

$\begin{array}{l}{d}^2\left(x_0,g_i{)}_{W^{-1}}={}_{ }{}^t(x_0-g_i)W^{-1}(x_0-g_i\right) \\ d^2{(}_{x_0}={}_{ }{}^{t}x{}_0{W}^{-1}{x}_0+{}_{ }{}^{t}g{}_i{W}^{-1}{g}_i-2*{}_{ }{}^{t}x{}_0{W}^{-1}{g}_i\end{array}$   2.18

The new individual will then be attributed to the group to which $d^2\left(x_0, g_i\right)$  in minimum.

If the dispersion of the values subjacent to each group differs significantly from one another, the exploratory analysis reaches its limits, as a new observation could be keen to be attributed to the group whose dispersion is the highest. To overcome this limitation, a statistical distribution hypothesis of the repartition of the observations in the space is usually needed, which will imply a probabilistic model underlying the multivariate sample.

Probabilistic context

Let $p_j$  be the proportion of observation in each group $j$ and $f_j\left(x\right)$  be the probabilistic distribution of $x$ of group $j$ . A new observation $x_0$  will be attributed to group $C_j$  where

$P\left(C_j\text{|}x\right)=\frac{p_j{f}_j\left(x\right)}{{{\displaystyle \sum }}_{j=1}^r{p}_j{f}_j\left(x\right)}$   2.19

is the highest. For any new observation, the denominator will always be equal to 1, so the affection can be deduced as maximizing

$p_j{f}_j\left(x\right).$   2.20

In case the data can be assumed to be from a truncated multivariate Gaussian model, its probability density function will be given by

$f_j\left(x\right)=\frac{1}{k{(2\pi )}^{\frac{p_j}{2}}\sqrt{\text{det}\left({\Sigma }_j\right)}} \exp \left[-\frac{1}{2}{}_{ }{}^t\left(x-{\mu }_j\right){\Sigma }_j^{-1}\left(x-{\mu }_j\right)\right]$ , where $k=\underset{{[0,4]}^{30}}{\overset{ }{{\displaystyle \int }}}{f}_j\left(x\right)dx$  2.21

Maximizing $f_j\left(x\right)$  is equivalent to maximizing its logarithm, as the logarithmic function is a strictly increasing function. Therefore, applying the logarithm to the maximization of equation (2.20) will be equivalent to

$Min\left[{}_{ }{}^t\left(x-{\mu }_j\right){\Sigma }_j^{-1}\left(x-{\mu }_j\right)-2\ln p_j+\ln (\text{det}({\Sigma }_j))\right].$   2.22

If there is equality between the variance and covariance matrices, the decision rule is linear. From equation (2.22), $\ln (\text{det}({\Sigma }_j))$ becomes constant and ${}_{}{}^t\left(x-{\mu }_j\right){\Sigma }^{-1}\left(x-{\mu }_j\right)$  is the Mahalanobis distance between and $x$ ,$${\mu }_j$$ ${\mu }_j$ which can be decomposed in

${}_{ }{}^{t}x{\Sigma }^{-1}x-2{}_{ }{}^{t}x{\Sigma }^{-1}{\mu }_j+{}_{ }{}^t\mu {}_j{\Sigma }^{-1}{\mu }_j.$   2.23

The term ${}_{ }{}^{t}x{\Sigma }^{-1}x$  of the equation above does not depend on group $j$ , therefore the maximization of $\text{ln}\left(p_j{f}_j\left(x\right)\right)$ can be written as

$Max\left[{}_{ }{}^{t}x{\Sigma }^{-1}{\mu }_j-\frac{1}{2}{}_{ }{}^t\mu {}_j{\Sigma }^{-1}{\mu }_j+\ln p_j\right]$   2.24

Let $x$ be a new observation. To attribute $x$ to group $i$ or $j$ , the linear discriminant scores are defined as

$W_{ij}={}_{ }{}^{t}x{S}^{-1}\left({\overline{x}}_i-{\overline{x}}_j\right)-\frac{1}{2}{}_{ }{}^t\left({\overline{x}}_i-{\overline{x}}_j\right)S^{-1}\left({\overline{x}}_i-{\overline{x}}_j\right)$   2.25

where ${\overline{x}}_i$  and ${\overline{x}}_j$  are unbiased estimators of the mean of groups $i$ and $j$ , respectively and $S$ is the unbiased estimator of the variance-covariance matrix $\Sigma$  defined by each group, calculated by

$S=\frac{1}{n-r}{\displaystyle \sum }_{i=1}^r\left(n_i-1\right)S_i$   2.26

where $S_i$  is the empirical variance matrix of group $i \left(i=1, \dots , r\right).$ ¹ The classification rule will be assigned individual $x$ group $i$ if $W_{ij}>0$ , for $i\ne j$ .

In the particular case where, the discriminant scores will be:

$W_{12}={}_{ }{}^{t}x{S}^{-1}\left({\overline{x}}_1-{\overline{x}}_2\right)-\frac{1}{2}{}_{ }{}^t\left({\overline{x}}_1-{\overline{x}}_2\right)S^{-1}\left({\overline{x}}_1-{\overline{x}}_2\right)$
$W_{13}={}_{ }{}^{t}x{S}^{-1}\left({\overline{x}}_1-{\overline{x}}_3\right)-\frac{1}{2}{}_{ }{}^t\left({\overline{x}}_1-{\overline{x}}_3\right)S^{-1}\left({\overline{x}}_1-{\overline{x}}_3\right)$
$W_{23}={}_{ }{}^{t}x{S}^{-1}\left({\overline{x}}_2-{\overline{x}}_3\right)-\frac{1}{2}{}_{ }{}^t\left({\overline{x}}_2-{\overline{x}}_3\right)S^{-1}\left({\overline{x}}_2-{\overline{x}}_3\right)$   2.27

Considering that, it is only required two of the equation’s terms to know the final one. As a result, the classification rule is defined as

• Classify the new individual to group 1 if $W_{12}>0$ and $W_{13}>0$
• Classify the new individual to group 2 if $W_{12}<0$ and $W_{23}>0$
• Classify the new individual to group 3 if $W_{13}<0$ and $W_{23}<0$

If ${\Sigma }_j$  is different among the groups under study, it will be necessary to compare $k$  quadratic functions of $x$ , being ${\Sigma }_j$  estimated by $\frac{n_j}{n_j-1}{\text{S}}_j$ , where ${\text{S}}_j$  is the empirical variance and covariance matrix of group $j$ , and ${\mu }_j$  estimated by the center of gravity of each group $g_j$ .

Box M test will be used to test the equality of the variance-covariance matrices between groups, being its hypothesis $H_0: {\Sigma }_1={\Sigma }_2=\dots ={\Sigma }_r$
$vs$
$H_1:\exists \left(r,j\right), with r\ne j and j<r: {\Sigma }_r\ne {\Sigma }_j$  

where $r$ is the total number of groups under study. The sensitivity of the Box M test to the lack of normality in the variable vector emphasizes the potential use of a significance level of 0.01 or lower.⁸

If the equality between the variance-covariance matrices cannot be assumed, quadratic discriminant analysis overcomes this problem, although it will be needed to estimate each, which will complexify the problem. Another problem associated with the use of quadratic discriminant analysis is when the sample sizes are small. It affects the robustness of the DFs obtained, so it may be better to use LDA either way.⁷

Contribution of variables

For the contribution of each variable to each DF, the coefficients are analyzed in absolute value, so that it is known if the variable of matter is or is not important to the problematic context. As for the interpretation of the DFs, the signs of the coefficients are important to determine the context of the variables under analysis.⁹ Three different approaches are suggested to analyze the contribution of each variable to discriminate the groups, namely the standardized discriminant function coefficients, the correlation between variables and the DFs, and perform partial F-tests.

The approach of analyzing the contribution of each variable to discriminate between groups may not provide the most accurate results since it does not consider the potential impact of other variables, which could lead to misleading conclusions.⁹

The standardized discriminant function coefficients enable the possibility of comparing each variable with one another, as the coefficients become-scale free. As a result, the coefficients will showcase the exact contribution of each variable to the corresponding DF.

Finally, the partial F-test is a statistical test whose objective is to show the relevance of each variable to the contribution of group separation. However, when there is more than one DF, the partial F-values cannot be associated with a DF, but with the overall contribution of the variable to the group discrimination. In opposition, if the weight of any eigenvalue is large enough, then most of the separability is accounted for the DF associated with such eigenvalue, and the variables, ordered according to their partial F-values, may produce similar results to those obtained by the standardized discriminant function coefficients.⁹

Stepwise discriminant analysis

Multicollinearity can influence the selection of discriminator variables. The absence of a specific variable does not necessarily mean the variables lack importance for the model. The omitted variable may be indeed capable of discriminating the groups, but its correlation with other variables does not allow it to be included in the model.¹⁰ Recurring to Variance Inflation Factors (VIF) it is possible to determine whether or not a variable is related to another.¹¹

Stepwise Discriminant Analysis combines both forward and backward approaches. In the forward approach, the model selects the variable with the highest partial F-statistic based on Wilk’s lambda at each step. As the analysis proceeds, the previously included variables are reevaluated to determine if any variable that has entered the model has become redundant due to newly included variables. This joint procedure continues until the largest partial F value among the included variables surpasses a predefined threshold. In the backward approach, the initial model includes all variables and, at each step, the variable with the lowest partial F values, in other words, the one that least contributes to the model, is removed from the model.⁹ Once the subset of discriminant variables is established, it will be useful to calculate the DFs and evaluate the performance of this discriminant procedure, namely, evaluating the percentage of misclassified observations using the sample test. This procedure could be referred to as Stepwise MANOVA (Multivariate Analysis of Variance). In such approach, no DFs are calculated at each step. After the selection of variables is achieved, the DFs and the misclassified rate matrix will be calculated.

To evaluate the effectiveness and reliability of each model, they will be evaluated through a testing set. Using testing sets is a reliable way of analyzing the overall performance of the model, as it is a process that helps ensure that the model performs reliably and accurately when applied to unseen data.

¹If $\Sigma$ is estimated by $S$ ($\frac{n}{n-p}W$ ) where $W$ is the within-group variance matrix), the Bayesian rule will correspond to the geometric rule under the equality of the probabilities a priori, so the geometric rule is then optimal.

The first steps of data processing, which were simulating TND values to create the samples, were done with the software RStudio, which uses R as the programming language. With the same software, it was possible to create boxplots, and Box’s M-test. JMP Pro 17 and SPSS were used to perform the discriminant analysis techniques.

For the preliminary data analysis, the variables will be compared within the same group, as the objective is to discriminate the three groups. The main purpose of analyzing parallel boxplots is to find the variables whose boxplots of each group are the furthest from one another.

The boxplot’s interpretation can be resumed in five different sets (Figure 1):

1. All three groups’ distributions do not seem to be different - variables Fatigue, Cramps, and Satiety – Figure 1A;
2. All three groups’ distributions seem to differ from one another – variables Nightmares, Muscle twitching, Tension, Heartburn, Horripilation, Headaches, Indifference, Memory, and Vague anxiety – Figure 1B;
3. The Healthy group differentiates itself from the other two groups, but there is no apparent differentiation amongst the other groups – variables Tremors, Knotted throat, Palpitations, Headaches, Dizziness, Pulse, Fainting, Eye floaters, Oppression, Attention, Memory, Indecision, Fear of the future, Apprehension of the worst, Fear of loneliness, Other fears, and Fear of crowds – Figure 1C;
4. The Nervous group differentiates itself from the other two groups, but there is no apparent differentiation amongst the other groups – variables Diarrhea and Tingling – Figure 1D;
5. The Psychotic group differentiates itself from the other two groups, but there is no apparent differentiation amongst the other groups – variable Muscle Pain – Figure 1E.

To enrich the exploratory statistical analysis, FDA will be performed with all thirty variables predicting the group to which an individual will be allocated, although it is noted that some variables might not be as useful to discriminate each group from one another.

Figure 1 Boxplot representation of the variables for the five possible cases of data distribution.

Considering multivariate data are generated from a truncated multivariate normal distribution, it is possible to perform the Box’s M test. The test statistic obtained was 1026.4, with a p-value of 0.015, so the null hypothesis is not rejected for the significance level fixed at most 0.01, considering the specific statistical properties of such test. Thus, the three groups can be assumed to have homogeneous covariance matrices. With these two assumptions, FDA can be performed on the whole data set.

Factorial discriminant analysis

From Figure 2, which showcases the dispersion of a hundred and fifty individuals, with each group centroid defined by a “+” sign, when represented by all variables, it is noted that the separation of the healthy group and the non-healthy groups is evident. It can then be inferred that the first DF will aim to separate the healthy group from the non-healthy groups, whereas the second DF will aim to separate nervous individuals from psychotic individuals.

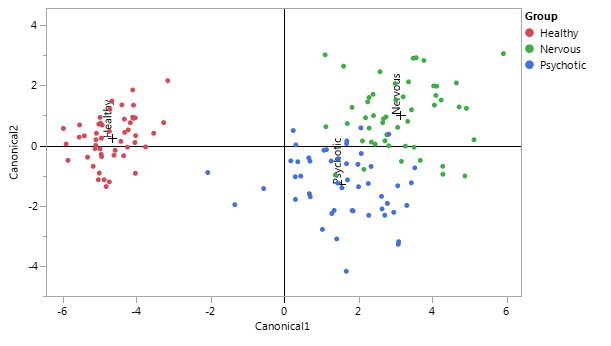
Figure 2 Representation of all thirty variables in the first factorial principal plane generated by the two discriminant functions.

The standardized scoring coefficients of each variable for each DF, represented in Table 4, indicate the contribution of the variable to the DF. Therefore, the further from zero the coefficient is, the more the variable will contribute to the discrimination of the three groups. From the set of thirty variables, the ones who have the biggest scoring coefficient in the first DF are variables (and respective standardized scoring coefficients in parenthesis) Palpitations (0.401), Heartburn (0.4), Apprehension of the worst (0.397), Oppression (0.381), and Fear of loneliness (0.35). For the second DF, it can be noticed that the variables that most contribute to the discrimination of groups Nervous and Psychotic are Palpitations (-0.507), Muscle pain (0.499), Muscle twitching (-0.480), Headaches (0.429), Tingling (0.415), and Tension (0.388). Palpitations and Muscle twitching contribute to the psychotic group, while the other three variables mentioned contribute to the nervous group.

The two eigenvalues obtained were 11.537 and 0.940. Consequently, the discriminant power of the first DF is 92.47% and the discriminant power of the second DF is 7.53%, which comes to prove that it will be easier to separate healthy and non-healthy individuals than it will be to separate nervous individuals from psychotic individuals. The two obtained DFs associated with the model are:

$\begin{array}{l}{C}_1=0.185*x_1+ 0.377 *x_2+ 0.292 *x_3 + 0.137 *x_4 + 0.088 * x_5 + 0.265 * x_6-0.077\\ * x_7+0.187 * x_8 -0.066*x_9+0.999 * x_{10}+ 0.278 *x_{11}+ 0.355 * x_{12}\\ + 0.482 * x_{13} -0.036 *x_{14}+ 0.061 *x_{15}+ 0.176 *x_{16}+0.347 * x_{17}\\ + 0.332 *x_{18}+ 0.069 *x_{19} + 0.467 *x_{20}+ 0.277 * x_{21}+ 0.121 * x_{22}\\ + 0.241 * x_{23}+ 0.251 *x_{24}+ 0.114 * x_{25}+ 0.243 *x_{26} + 0.427 * x_{27}\\ +0.433 * x_{28} + 0.065 * x_{29}+0.299 *x_{30} - 8.791\end{array}$   4.1

$\begin{array}{l}{C}_1=0.218*x_1+ 0.147 *x_2-0.662 *x_3 + 0.079 *x_4 + 0.037 * x_5 \\ + 0.447 * x_6+0.668 * x_7+0.104 * x_8 +0.264*x_9+0.505 * x_{10}\\ + 0.388 *x_{11}+ 0.19 * x_{12}-0.609 * x_{13}+0.51 *x_{14}+ 0.13 *x_{15}\\ + 0.578 *x_{16}-0.111 * x_{17}- 0.362*x_{18}+ 0.199 *x_{19}-0.11 *x_{20}\\ + 0.053 * x_{21}+ 0.088 * x_{22}- 0.317 * x_{23}+ 0.143 *x_{24}+ 0.024 \\ * x_{25}- 0.074 *x_{26}- 0.074 * x_{27}-0.1 * x_{28}- 0.248 * x_{29}+0.212 \\ *x_{30} - 2.631\end{array}$   4.2

where $x_1=$  Fatigue, $x_2=$ Nightmares, $x_3=$ Muscle twitching, $x_4=$ Cramps, $x_5=$ Tremors, $x_6=$ Tension, $x_7=$ Muscle pain, $x_8=$ Knotted throat, $x_9=$ Satiety, $x_{10}=$ Heartburn, $x_{11}=$ Diarrhea, $x_{12}=$ Horripilation, $x_{13}=$ Palpitations, $x_{14}=$ Headaches, $x_{15}=$ Dizziness, $x_{16}=$ Tingling, $x_{17}=$ Pulse, $x_{18}=$ Fainting, $x_{19}=$ Eye floaters, $x_{20}=$ Oppression, $x_{21}=$ Indifference,$x_{22}=$ Attention, $x_{23}=$ Memory, $x_{24}=$ Indecision, $x_{25}=$ Vague anxiety, $x_{26}=$ Fear of the future, $x_{27}=$  Apprehension of the worst, $x_{28}=$ Fear of loneliness, $x_{29}=$ Other fears, and, $x_{30}=$ Fear of crowds. When testing the likelihood ratio test, the p-value obtained for each DF, $C_1$ and $C_2$ , was below 0.01, justifying the use of both DF to discriminate the three groups under study.

Representing the classifications attained from the training set in the first FDA performed, Table 5 shows that the healthy individuals are not for once mistaken with individuals from any other group, leading to a perfect classification of the Healthy group, and only one individual (from the Psychotic group) is misclassified for healthy. In addition, the percentage of individuals that were misclassified is 4.(6)% (3 individuals from the nervous group and four individuals from the psychotic group, out of the total 150 individuals).

To validate the models’ accuracy in discriminating the three groups, the model was submitted to a testing set. The testing set contained seventy-five new individuals, evenly distributed by the three groups, generated from the same TND as the training sample. A misclassification rate of 10.(6)% was obtained and, in Table 6, it can be seen that the model was able to perfectly classify healthy individuals, while the psychotic individuals were only once mistakenly classified as healthy individuals. As a result, it can be said that the model was able to discriminate the three groups predominantly correctly. To further analyze the three groups on behalf of this paper’s main objective, two different approaches are referred to analyze the behavior of each variable to the DFs.

From Table 7, with the partial F test statistic and p-values associated with the test statistic obtained for each variable, it can be seen that variables Fatigue, Cramps, and Satiety are not significantly contributing to the discriminant model created, as their p-value is superior to 0.28, which goes according to the exploratory analysis previously made.

From Table 8, it is observed that the correlations between the variables and the two DFs are bigger in the first DF than it is in the second one. One of the main causes is the percentage of the variance of the first DF being 92.47%, while the second DF covers the remaining 7.53%, as previously stated. The correlation between the variables to the first DF goes as high as 0.693 (Fear of crowds) to as low as -0.096 (Muscle pain). For the second DF, the correlation goes as high as 0.391 (Muscle twitching) to as low as -0.437 (Tingling). When analyzing the correlation with the first DF, only two variables are negatively (and weakly) correlated. It is noted that variables Tingling, Muscle pain, and Tension with correlations 0.437, 0.403, and 0.37, in the order mentioned, best describe the psychotic group, while the variables that best describe the nervous group are Muscle twitching, Palpitations, and Other fears with correlations -0.391, -0.277, and -0.234 in the respective order.

Based on the analysis conducted on the contribution of each variable to FDA, the variables that indicate a good separation amongst the three groups are Muscle twitching, Muscle pain, Tension, Heartburn, Horripilation, Palpitations, Headaches, Tingling, Pulse, Fainting, Oppression, Indifference, Apprehension of the worst, Fear of loneliness, and Fear of crowds. Variable Muscle pain has a standardized coefficient of 0.499 with the second DF and a correlation with the same DF of 0.403. For this reason, the variable was chosen to be included in the model, as it is an important variable to discriminate both unhealthy groups from each other. Variables Headaches and Tingling were also chosen to take part in the model as their correlation to the second DF and standardized scoring coefficients were high when compared to other variables. Although the partial-F values were not the highest, the variables had to take part in the model to give more weight to the discrimination of Nervous and Psychotic groups, otherwise, the model’s focus would be to only discriminate healthy and unhealthy groups. Still, variables Fear of crowds, Fainting, Oppression, Apprehension of the worst, Indifference, Pulse, and Fear of loneliness were chosen as their behavior was very focused on separating the Healthy group from the two others. Variables Muscle twitching, Tension, Heartburn, Horripilation, Palpitations, and Fainting are variables that have a remarkable performance to discriminate the groups under study, the reason being choosing them to take part in the new model.

Reduced model

As any subset of the initial thirty variables also follows a multivariate normal distribution, the question is just to re-analyze the homogeneity of the covariance matrices among the three groups under the reduced model. The test statistics obtained for Box’s M test was 280.88, with a p-value of 0.04, from which the null hypothesis is not rejected.

From Figure 3, it is clear that the dispersion of the three groups has increased, although it is still noticeable that the dispersion of the healthy group is smaller than the other two groups. It is also visible that there is a greater mix of individuals in the nervous and psychotic groups, which indicates a bigger misclassification rate in this group.

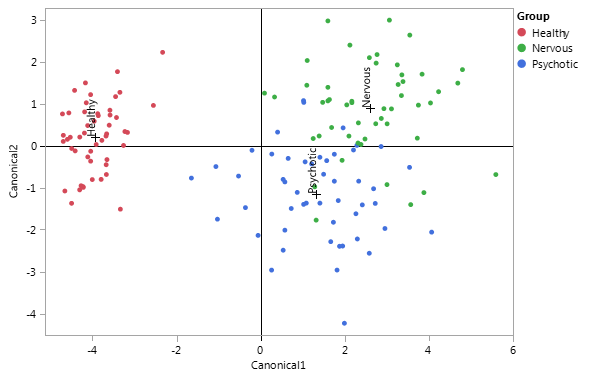
Figure 3 Representation of the proposed variable selection (15 variables) in the first factorial principal plane generated by the two discriminant functions.

The standardized scoring coefficients are represented in Table 8, and as expected, all variables have a high standardized coefficient. In either one of the two functions, each variable shows how it behaves in accordance with the function. For instance, despite variable Headaches having a near-zero standardized scoring coefficient with the first DF, it has one of the highest standardized scoring coefficients in the second DF.

From this FDA produced, the two new eigenvalues associated with the first and second DFs, respectively, were 8.158 and 0.739, which corresponds to a discriminant power of 91.69% and 8.31%. The two DFs subjacent to the model were the following:

$\begin{array}{l}{C}_1=0.194\text{*}{x}_1-0.158\text{*}{x}_2+0.247\text{*}{x}_3+1.107\text{*}{x}_4+0.447\text{*}{x}_5+0.59\text{ *}{x}_6-0.002\text{*}{x}_7\\ +0.254\text{ *}{x}_8+0.567\text{ * }{x}_9+0.35\text{*}{x}_{10}+0.478\text{*}{x}_{11}+0.396\text{*}{x}_{12}+0.382\text{*}{x}_{13}\\ +0.494\text{*}{x}_{14}+0.257\text{*}{x}_{15}-6.113\end{array}$   4.3

$\begin{array}{l}{C}_2=-0.66*x_1+0.616*x_2+0.467*x_3+0.493*x_4+0.138*x_5-0.396*x_6+0.501*x_7\\ +0.559*x_8-0.048*x_9-0.4*x_{10}-0.046*x_{11}+0.125*x_{12}-0.035*x_{13}\\ -0.185*x_{14}+0.201*x_{15}-1.797\end{array}$   4.4

where $x_1=$  Muscle twitching, $x_2=$ Muscle pain, $x_3=$ Tension, $x_4=$ Heartburn, $x_5=$ Horripilation, $x_6=$ Palpitations, $x_7=$ Headaches, $x_8=$ Tingling, $x_9=$ Pulse, $x_{10}=$ Fainting, $x_{11}=$ Oppression, $x_{12}=$ Indifference, $x_{13}=$ Apprehension of the worst, $x_{14}=$ Fear of loneliness, and, $x_{15}=$ Fear of crowds. The p-value obtained for each DF,$C_1$ and $C_2$ , in the likelihood ratio test was below 0.01, justifying the use of both DF to discriminate the three groups under study.

From the visualization of Table 9, it can be seen that a misclassification rate obtained for the training set of this model was 10%, where it was registered seven nervous individuals that were classified as psychotic, and eight psychotic individuals were misclassified, from which seven were classified as nervous and one as healthy.

When submitted to the testing set previously created, the percentage of misclassification obtained was 14.(6)%, where it is important to emphasize that the model was still able to perfectly classify healthy individuals into their group, visible in Table 10. The biggest rate of misclassification is present in the classification of nervous individuals to psychotic individuals, and vice versa. As expected, reducing the number of variables to fifteen implies a bigger misclassification rate. On the other hand, fifteen fewer variables are needed to maintain an expressive classification rate.

Stepwise discrimination

To analyze the presence of multicollinearity, Table 11 reveals that it will not be a problem among the variables. Almost all variables have VIF values between one and two, indicating few signs of multicollinearity. For those values whose VIF exceeds two, the Tolerance values are superior to 0.4, and remembering that multicollinearity is assumed when tolerance is below 0.1, then multicollinearity is not considered in the variables under study.

The stepwise method took an optimal eighteen iterations, and the following eighteen variables were chosen to take part in the stepwise model: Fear of crowds, Fainting, Fear of loneliness, Horripilation, Nightmares, Heartburn, Palpitations, Pulse, Apprehension of the worst, Tension, Muscle twitching, Oppression, Indecision, Muscle pain, Memory, Headaches, Tingling, and Indifference. Each variable is enumerated in the order it entered the model.

The interpretation of the data dispersion does not fall far from the other interpretations made, as there is a clear separation of the healthy individuals and the unhealthy individuals, which can be seen in Figure 4. The dispersion of individuals in each group is also maintained, where it is clear that the healthy individuals are closer to their group centroid when compared to either the nervous or psychotic individuals, which are more spread out.

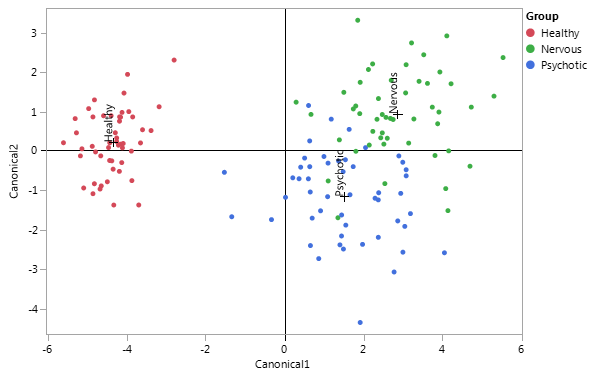
Figure 4 Representation of the eighteen variables obtained from stepwise discrimination, represented in an orthogonal axis generated by the two discriminant functions.

The eigenvalues obtained for the performed model were 9.967 and 0.772, respectively for the first and second DF, which can be interpreted as the first DF having a discriminant power of 92.81% and the second DF having a discriminant power of 7.19%.

In the training set of the model, a total of fifteen individuals out of the total one hundred and fifty were misclassified, visible in Table 12, which corresponds to a misclassification percentage of 10%. Of the fifteen misclassified individuals, six belong to the nervous group and were classified as psychotic, while eight psychotic individuals were classified as nervous and one psychotic as healthy. On the other hand, the individuals who belong to the healthy group were not, for once, misclassified.

When submitted to the testing set, the model obtained a misclassification apparent rate of 16%. The misclassifications were all prevenient from the nervous and psychotic groups, which can be seen in Table 13. Equivalently to the two other models analyzed, healthy individuals are accurately classified, which is a demonstration of how the set of variables can correctly recognize the patterns and characteristics of healthy individuals.

In summary, the stepwise model has shown itself to be an effective classification model. On one hand, when comparing this model with the one with thirty variables, the misclassification percentage is higher in both the training and the testing set. However, the increase in the misclassification percentage is justified by the use of fewer variables.

It is noted that the model created with thirty predictive variables obtained the best results. The misclassification apparent rate was 4.(6)% and 10.(6)%, respectively for the training and testing set. This result was proven to be counter-productive, as the exploratory data analysis provided useful information on the variables that could be excluded from the analysis to reach the study’s objective. Additionally, the interpretation of the correlation between variables and the DFs, partial F-tests, and the standardized discriminant function coefficients corroborated the suspicions raised by boxplot analysis. These four methods working together resulted in a set of fifteen variables. This new set was then used to perform FDA and create a new, reduced model, resulting in a misclassification rate of 10% in the training set and 14.(6)% in the testing set.

To further validate if the use of the fifteen variables provided a reliable result, the model was compared to a stepwise discrimination model with eighteen variables. This stepwise model obtained a misclassification apparent rate of 10% in the training set and 16% in the testing set. As a result, the reduced model provides a more reliable model to classify individuals into one of the three groups. The misclassification rate obtained in the training set was the same, but the reduced model had a better performance in the testing set.

When comparing the reduced model to the full model, it was verified that the full model is a better classifier both in the training and in the testing set, as expected, but the complexity and accuracy of the reduced model compensate for choosing the reduced model over the full model. As the main objective of this study is to help early diagnosis of mental illnesses, such as nervousness or psychosis, the larger misclassification rate in both training and testing sets is acceptable.

It is also important to note that all the fifteen variables selected to take part in the reduced model took part in the stepwise model created, being the only difference between the two models’ variables Nightmares, Indecision and Memory. Although these variables were not considered for the reduced model, they could provide relevant information for the patient’s classification when it is not possible to obtain information from one of the fifteen chosen variables.

Several limitations underlined to DA should be noted. Firstly, the DFs developed may not be generalizable to other populations or samples, as the model is based on the specific characteristics of the sample used. However¹², have demonstrated that DFs can be effectively applied across similar samples, and¹³ suggest a generalization to help in the verification of food quality. Additionally, this study is subject to the limitations inherent to DA, such as the reliance on certain assumptions about the distribution of variables and the relationship between predictor variables and group membership, as well as the sensitivity to missing data and the limited ability to handle non-linear relationships. Furthermore, the more groups that are considered, the greater the risk of misdiagnosis for individual subjects. It is recommended to minimize the number of predictor variables to avoid creating an overly complex model, which would also increase the difficulty in interpreting the conclusions.

While DA is prone to be a useful tool in the diagnosis of ADs, it should not be used as the sole method of diagnosis. It is important to consider a range of factors, including the patient's medical history and the results of other exams, to make an accurate diagnosis. It is also important to note that DA is a statistical method and is subject to certain limitations and assumptions, as discussed earlier. Therefore, it is advisable to use DA in conjunction with other methods and to carefully evaluate the results in the context of the individual patient.

This research illustrates once again the effectiveness of DA, more precisely FDA, to affect individuals to pre-established groups. In all three models created, it is noteworthy that the characteristics and patterns of the Healthy group were consistently recognized by each model, leading to a misclassification apparent rate of 0% for healthy individuals. While the accuracy for nervous and psychotic individuals was not as high, the model still managed to get promising results that can contribute to the diagnostic process.

For the established objectives of this paper, the first model created demonstrated a consistent ability to predict to which one of the three groups, healthy, nervous, or psychotic groups, a new individual was mostly likely considered to be. Out of the thirty initial variables used to perform FDA, it was possible to reduce half of the variables while maintaining the expected performance. In addition, it was necessary to use two DFs to effectively separate the three groups under study. The first DF’s objective was to separate healthy from unhealthy individuals, while the second DF’s purpose was to separate both unhealthy groups. The error rate obtained from the training set is biased, and, as a result, it was not used as a measure to validate the DFs. Nowadays, several approaches are available to face this question. A complementary validation study using different approaches to validate the DFs is being prepared. Namely, the holdout method, and the bootstrap validation may be used, which will result in an unbiased estimate of the classification rate.

Although the use of only fifteen parameters has proved to be an option for diagnosing an individual’s mental state, the model should not be used exclusively to classify patients. MDs are highly delicate issues, and it is essential that supplementary studies and assessments are carried out on a case-by-case basis before any conclusions are drawn.

This study focused its methodology on FDA, but a non-parametric approach could be used, as the borderline between the assumption of multinormality subjacent to data dispersion and the equality of variance-covariance was almost crossed. It could be interesting to recreate the same study without being restricted to parametric discriminant analysis assumptions. This would allow larger flexibility on the dataset used to conduct the study. The behavior of individuals may change, leading to heterogeneity of data dispersion. Investigators could try approaching data classification by ranking observations, and distribution-free techniques.

The authors declare that there are no conflicts of interest.

None.

None.

1. Gissler M, Laursen TM, Ösby U, et al.Patterns in mortality among people with severe mental disorders across birth cohorts: a register-based study of Denmark and Finland in 1982–2006. BMC Public Health. 2013;13(1):834.
2. Walker ER, McGee RE, Druss BG. Mortality in mental disorders and global disease burden implications: A systematic review and meta-analysis. JAMA Psychiatry. 2015;72(4):334–341.
3. Remes O, Brayne C, van der Linde R, et al. A systematic review of reviews on the prevalence of anxiety disorders in adult populations. Brain Behav. 2016;6(7):e00497.
4. The Biological Effects and Consequences of Anxiety. Anxiety Care; UK. 2023.
5. Batelaan NM, Seldenrijk A, Bot M, et al. Anxiety and new onset of cardiovascular disease: critical review and meta-analysis. Br J Psychiatry. 2016;208(3):223–231.
6. Nasrallah HA. Consequences of misdiagnosis: inaccurate treatment and poor patient outcomes in bipolar disorder. J Clin Psychiatry. 2015;76(10):e1328.
7. Saporta G. Probabilités, analyse des données et statistique. 3rd ed. France: Technip editions; 2011.
8. Olson CL. Comparative robustness of six tests in multivariate analysis of variance. J Am Stat Assoc. 1974;69(348):894–908.
9. Rencher AC. Methods of multivariate analysis. 2nd ed. New York : Wiley; 1995.
10. Sharma S. Applied multivariate techniques. New York: Wiley; 1995.
11. Miles J. Tolerance and variance inflation factor. John Wiley & Sons; 2014.
12. Ma G, Zhang Y, Zhang J, et al. Determining the geographical origin of Chinese green tea by linear discriminant analysis of trace metals and rare earth elements: taking Dongting Biluochun as an example. Food Control. 2016;59:714–720.
13. Esteki M, Shahsavari Z, Simal-Gandara J. Use of spectroscopic methods in combination with linear discriminant analysis for authentication of food products. Food Control. 2018;91:100–112.