Amid the relentless spread of COVID-19 pandemic, India spiked to the fifth rank among the nations on the daily increase of death toll during August 2020. In this scenario, the study mainly focuses on appalling and unprecedented COVID-19 mortality in India. The most adaptable epidemiological index for measuring the severity of the disease is Case Fatality Rate (CFR) and is estimated using the Yoshikura method. The estimated CFR of 10 states in India is compared along with the general formula of CFR and Kerala is found to be having the least CFR of 0.40% indicating the least severity of disease. The steadily increasing deaths in India are modelled using probability distributions such as Weibull, Gamma, and Lognormal in order to obtain the best fitted model with the data. The study demonstrated that the Gamma distribution is  the best fitting probability model. Time-series modelling is used to analyse the trend and forecasting pattern of mortality. The ARIMA model indicates an ascending trend of death in upcoming days and this prescient model gives help to the administrative authorities and medical personnel in health care service and infrastructure arrangements in forthcoming days. The major mitigation step to resolve and restrain the pandemic is vaccination.

Keywords: COVID-19, CFR, yoshikura method, distribution, time series analysis, ARIMA

In India, the spread of novel coronavirus has accelerated with new cases and deaths being reported daily. Following the first confirmed positive case reported in Kerala on January 30, the epidemic has expanded its footprints in the country. As of August 6, COVID-19 counts proliferated in India, confirming 20, 25,423 cases and reporting 41653 deaths. According to the Ministry of Health and Family Welfare, Maharashtra is the most affected state. It is expected to cross one crore by the end of December in India.

On March 4, the WHO Director-General, Dr Tedros Adhanom Ghebreyesus commented that 3.4% of COVID-19 cases have died around the world. The COVID-19 pandemic has grown into a major health crisis worldwide. Not only does it pose a huge threat to public health but it also affects the social, economic and cultural aspects. Health and social services are rapidly growing to address this emergency.

Rapid viral transmission has also changed our lifestyle. Hence the identification of the impact of SARS-coV-2 in our own lives is of utmost importance. To understand the severity of the epidemic among cases, a common epidemiological practice is to estimate the Case Fatality Rate. This study speaks briefly about the CFR estimation of the top 10 ranked states in the NITI Aayog Health Index. The strategy utilized in acquiring the CFR is the Yoshikura technique. The evaluated Yoshikura estimate is compared along with the general equation of CFR to check the precision of the model. Also, in this study, deaths based on the daily reported data are fitted to various distributions in order to find the best fit model. Mathematical models provide a quantitative framework to test hypotheses on the possible underlying mechanisms that explain trends at various spatial and temporal scales in the observed results. CFR is beneficial to find the severity of COVID-19 calculated using cases and death. The small fluctuation in the value of CFR is depicted through forecasting. In this study, a time series model is developed and then employed for forecasting future demise in India. The ARIMA model predicts the likely development of pandemic.

The COVID-19 dataset of India is collected from JHU-CSSE (2020), the GitHub repository provided from March 12, 2020, to July 31, 2020.The variables include confirmed cases, cured cases and deaths. This data is further used to compare the mortality using CFR and then to forecast and fit the COVID-19 deaths. In this paper, the mortality rate of the pandemic of the first 10 ranked states in the NITI aayog Health Index is compared. The states are Kerala, Andhra Pradesh, Maharashtra, Gujarat, Punjab, Himachal Pradesh, Jammu and Kashmir, Karnataka, Tamil Nadu and Telangana. Besides the fatality it is of significance to incorporate measures such as Mortality Rate (MR), and Recovery Rate (RR) which gives a better idea about the strict measures and the care taken by health professionals in preventing deaths due to COVID-19. Among these three measures, CFR is the most significant marker for mirroring the infection severity dependent on mortality.

 Case fatality rate (CFR)

To recognize the severity of the infection, determine the effects of public health measures and anticipate the probable number of deaths in the population given the total number of people infected,it is of utmost importance to measure the real time during the early stage of an epidemic.⁴ CFR is obtained as the proportion of cases of a specified condition that are fatal within a specified time.

 CFR = $\frac{Number of death due to COVID-19}{Total number of cases of COVID-19 }$ times; 100     (1)

But this value is often known to be flawed, frequently underestimating the actual CFR. The study is put forward to obtain a precise estimate by employing the Yoshika method.

 Yoshikura method for estimating CFR

Let X is the cumulative number of cases and Y is the cumulative number of deaths respectively. Yoshikura method³ involves the linear relationship between log X and log Y and the model is represented as follows

$logY=klogX+L$     (2)   

The CFR can be expressed as

$p\text{^}(X/N0)k/X$     (3)

 where,  is the estimate.

$N_0=exp\left(-intercept/slope\right)$     (4)

The coefficient ‘k’ is the slope of the straight line and, N₀ is the number of those confirmed cases that occurred before the first pandemic related death. Hence, the CFR of the top 10 ranked states is obtained. Thereby the states with most and least values of CFR are obtained. The higher CFR value suggests a significant death toll. In the case of COVID-19, the CFR acts as a better estimate for understanding the outbreak and epidemiological features of the disease, and thus get more ideas on the severity of disease.⁴ Along with CFR, certain measures such as Mortality rate(MR) and Recovery rate(RR) are added that are helpful in comparison and gaining knowledge of the states.

Mortality rate,

 MR = $\frac{Number of deaths due to COVID-19 }{Total Population}$ × 100000     (5)

Recovery rate

 RR = $\frac{Number of people recovered from COVID-19}{Number of COVID-19 cases with outcome}$ × 100     (6)

 Distribution modeling

In the next stage, the statistical distribution that best fits the data of COVID-19 mortality in India is evaluated using the MLE method. The first step is the choice of candidate distributions for fitting distributions to the data. Henceforth histogram and empirical distribution was plotted to check the normality and afterward the data was obtained as right-skewed. In order to describe a distribution among a set of parametric distributions, descriptive statistics is used to choose candidates. Weibull, Gamma and Lognormal distributions are chosen in order to find the best fitted distribution among them. $f\left(.|\theta \right)$ (with parameter ) $\theta \in R^d$ was fitted to the data set, one at a time, after selecting one or more parametric distributions .

 Weibull distribution: The probability density function of a Weibull random variable is:

$f\left(x;\lambda ,k\right) = \frac{k}{\lambda }{\left(\frac{x}{\lambda }\right)}^{k-1}{e}^{{\left(-\frac{x}{\lambda }\right)}^k} x \ge 0$     (7)

where k > 0 is the shape parameter and is the scale parameter of the distribution.⁶

 Gamma distribution: The pdf of a Gamma random variable is:

$f\left(x,\alpha ,\lambda \right) =\frac{{\lambda }^{\alpha }}{\Gamma \left(\alpha \right)}{x}^{\alpha -1}{e}^{-\lambda x};x\in R^{+}$     (8)

Lognormal distribution: A positive random variable X is log-normally distributed if the logarithm of X is normally distributed.⁷

$Ln(X)~ N(\mu ,{\sigma }^2)$     (9)

Distribution parameters were by default estimated by maximizing the likelihood function defined as:$L\left(\theta \right)={\displaystyle \prod }_{i=1}^{n}f(xi |\theta )$ according to the i.i.d. sample assumption, where $x_i$ is $n$ the observations of variable $Xandf\left(.|\theta \right)$ is the density function of the parametric distribution. (Figure 1, Figure 2.1)

Figure 1 Comparison of Crude CFR and Yoshikura CFR.

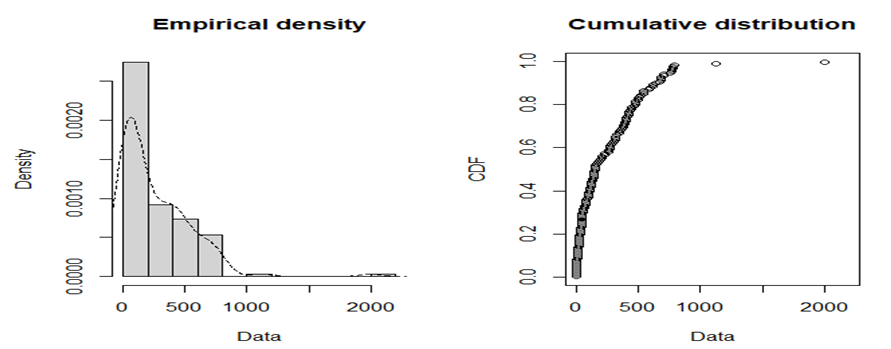
Figure 2.1 Histogram and CDF plots of an empirical distribution fitted to the COVID-19 deaths in India.

Four classical goodness-of-fit plots are plotted (Figure 2.2). These plots helped to determine the best fit distribution. The maximum goodness of fit estimation is done using Kolmogorov-Smirnov statistic. A maximum log-likelihood value and lower AIC and BIC value is the criterion for finding the best fit among the distributions. In this study, the AIC values of the three distributions are compared and the distribution with the lowest AIC value was selected as the best fitted model to the data.⁵

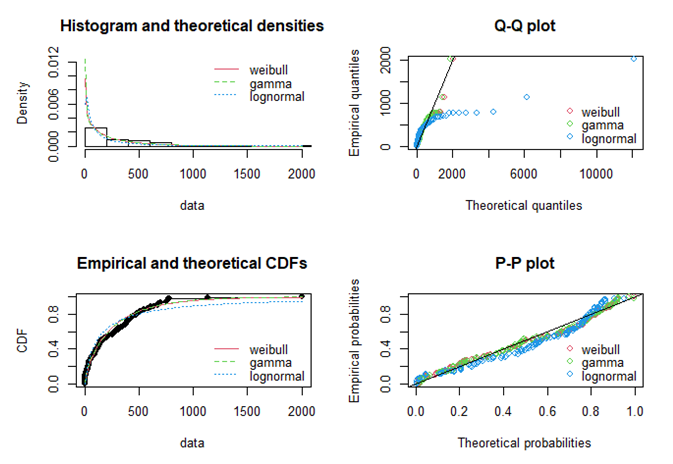
Figure 2.2 Four goodness-of-fit plots for Weibull, Gamma and Lognormal distributions fitted to the COVID-19 deaths in India.

Time-series modelling

The trend and forecasting pattern of mortality of infection in India due to COVID-19 is obtained using Time-series modelling. ARIMA modelling is one of the best modelling techniques for forecasting a time series.⁸ The main aspect of time series analysis and modelling is the consideration of autocorrelation. ARMA models combine autocorrelation methods (AR) and moving averages (MA) with time-dependent parameters. When differencing is included in the procedure, it becomes ARIMA (p,d,q) or Box-Jenkins modelling where ‘p’ stands for the order of auto-regression, ‘d’ signifies the degree of trend difference and ‘q’ is the order of moving average.⁹

In this method, the time pattern changes after a specific point, and is examined further to find out the nature of change and potential causes. Box Jenkins modelling primarily includes the evaluation of the stationarity of the data using Augmented Dickey Fuller test.¹⁰ The existence of trend and periodicity would result in non-stationarity. In order to remove these effects, the differencing stage is included until the time series becomes stationary. Then ACF and PACF are plotted which are useful in identifying and modelling patterns in time series. When modelling is completed, the result will be summarized or integrated to produce the estimations and forecast. The ARIMA model is fitted to the resulting time series by using an automated process.

The ARMA (p,q) model is given by:

_{$y_t=c+{\Phi }_1{y}_{t-1}+{\Phi }_2{y}_{t-2}+{\Phi }_3{y}_{t-3}+\dots +{\Phi }_p{y}_{t-p}+{€}_t–{\theta }_1{€}_{t-1}–{\theta }_2{€}_{t-2}-\dots -{\theta }_q{€}_{t-q}$}     (10)

The ARIMA (p,d,q) is given as

$y{’}_t=c+{\Phi }_{1}y{’}_{t-1}+{\Phi }_{2}y{’}_{t-2}+{\Phi }_{3}y{’}_{t-3}+\dots +{\Phi }_{p}y{’}_{t-p}+{€}_t–{\theta }_1{€}_{t-1}–{\theta }_2{€}_{t-2}-\dots -{\theta }_q{€}_{t-q }$     (11)

 Where $\left\{y_t\right\}$ is the data of daily COVID-19 deaths in India and${\Phi }_{1,}{\Phi }_{2,},\mathrm{..}, {\theta }_1, {\theta }_2\mathrm{..}$ are coefficients and $y{’}_t$ is the differenced series, the predictors on the right-hand side include both lagged values ${€}_t$ and lagged errors.¹⁰ Here the model estimated by the automated process has the lowest AIC value. The least value of AIC gives a more accurate model with the best fit. The AIC is defined as,

$AIC=-2\left(loglikelihood\right)+2K$     (12)

where K is the number of estimated model parameters.

After model estimation, diagnostic checking of the model is conducted which involves residual analysis. The model adequacy is primarily related to the assumption that residuals should be independent and identically distributed (iid). Also, the residuals should be uncorrelated. They were examined by using the autocorrelation function (ACF), Partial autocorrelation function (PACF), ADF test and Ljung- Box test.¹¹

The statistical analysis is done using R (version 4.0.0).

Table 1 shown below represents the obtained values of MR, RR, Crude CFR, and the Yoshikura estimate of CFR. The data required was collected from March 12, 2020 to July 31, 2020. Kerala has the least CFR of 0.40% indicating the least severity and Gujarat has the highest CFR of 5.25% representing the acme of the epidemic. The states with comparatively low CFR other than Kerala are Himachal Pradesh of, 0.49%. Maharashtra of, 4.21%is the state with comparatively high CFR next to Gujarat. Kerala is one among the states with lowest mortality rate of 0.218523.

 For evaluating the statistical distribution that best fits the data, 142 daily data of India were taken from 12 Mar to July 31, 2020. All the variables are summarized below using descriptive statistics. Table 2.1 reflects the descriptive statistics with a skewness and kurtosis of 2.1750 and 12.0926 respectively indicating the deviation from normality to right skewed distribution. Figure 2.1 depicts the histogram and CDF plot indicating the right skewed distribution graphically. Figure 2.2 portrays the goodness of fit plots of Weibull, Gamma and Lognormal distributions. These plots helped in determining the best fit model.

Table 2.2 demonstrates the estimate and standard error of the unknown parameters of Weibull, Gamma and Lognormal distributions along with the Log Likelihood, AIC and BIC values using the MLE method. Hence, it is obtained that the Gamma distribution owns the maximum Log likelihood value.

Table 2.3 reflects the goodness of fit using Kolmogorov-Smirnov statistic. Henceforth the Gamma distribution is identified as the best fit as it satisfied the criteria of having lower AIC value of 1786.985 when compared to others.

 Hence from Table 2.2, shape parameter α = 0.6912 and rate parameter λ = 0.0025

Therefore, the fitted Gamma distribution model is obtained as follows:

$f\left(x,\alpha ,\lambda \right)=0.026377 x^{-0.1584}{e}^{-0.015267 x}; x\in R^{+}$     (13)

  For forecasting the future COVID-19 death, the daily death of India has been collected from March-10 to July-31. The time series data is analysed using the ARIMA model. Hereby using the Auto-ARIMA which builds high-performance models with least AIC value. ARIMA (0,1,1) with AIC value of 1709.94 is attained. The model is then evaluated by residual analysis.  (Figure 3.1, Figure 3.2)

Figure 3.1 Time series plot of COVID-19 Deaths in India.

Figure 3.2 Plot for diagnostic checking.

The fitted model of ARIMA (0,1,1) is given as:

$Z_t=Z_{t-1}+a_t+0.8923a_{t-1}$     (14)

To forecast the future mortality of COVID-19 using the ARIMA (0,1,1) model and values are interpreted in Table 3.1 and the forecasted plot is given as in Figure 3.3 indicating an increasing pattern of future demise.

Figure 3.3 Forecast plot of COVID-19 mortality.

The patterns from the data reveal the prompt and effective approaches being taken and to be taken to minimise the mortality of the human population. This study mainly focuses on evaluating the severity of COVID-19 in the top 10 ranked states listed in NITI Aayog Health Index using Yoshikura estimate of CFR. Kerala has the least CFR estimate of 0.40% and Maharashtra has the second most elevated CFR estimate of 4.21%. Gujarat tops the list with higher CFR value of 5.25%.The Yoshikura CFR values corresponding to Maharashtra and Gujarat doesn’t show much significant difference and thus it might shift in like manner sooner rather than later. Since Kerala has the least CFR, it can be presumed that the system including treatment, infrastructure, awareness is more worthy than other states.

A demonstration based on the distribution of COVID-19 daily deaths in India was done with Weibull, Gamma & Lognormal in order to validate the best fitted model. Gamma distribution was obtained as the best fitted distribution among the other distributions as it satisfied the criteria of having lower AIC value of 1783.389. Here the estimated shape parameter of Gamma distribution has a low value of 0.653 indicating the data as right skewed. The smaller the shape parameter, the more the distribution tends to be skewed to the right suggesting least probability of deaths. Therefore, if the shape parameter becomes much smaller than the current, then there could be a possible decrease in the probability of death even further. Hence in the present study, the Gamma distribution indicates that the number of deaths is smaller and could possibly be the same with appropriate stringent measures.

Forecasting future deaths to strengthen the measures for minimising the death toll is a criterion to know the effect of an epidemic in the near future. An estimate of future death on a daily basis is obtained by employing the time series to propound mortality in India. An ARIMA (0,1,1) model with low AIC value is obtained and is used to forecast COVID-19 death. Based on the known number of deaths, an increasing pattern of the predicted death is obtained. Even during the restricted lock down period, it shows an increasing trend of demise which indicates that death risk won’t reduce for the next few months. Forecasted values of future deaths are exceptionally vital to support the medical authorities to be prepared for the upcoming events with more readiness in the healthcare system.

The authors are grateful to Mr. Noel George, Bio-statistician, P-value Solutions Pala for the valuable advice during this research project.

The author declares there are no conflicts of interest.

1. Kobayashi T, Jung SM, Linton NM, et al. Communicating the risk of death from novel coronavirus disease (COVID-19). Journal of Clinical Medicine.2021;9(2).
2. Mukhopadhyay I. NITI aayog health index: wrong symptoms and an erroneous diagnosis. Social Change. 2019;49(4):678–685.
3. Zheng Chene, Zihnag Lu. Estimation of timely case fatality risk for an ongoing infectious disease using daily case notification data –eAppendix.2015.
4. Kim DH, Choe YJ, Jeong JY. Understanding and interpretation of case fatality rate of coronavirus disease 2019. Journal of Korean Medical Science. 2020;35(12):e137.
5. Elham G, Kamyar M, Mojtaba SK. Statistical distribution of novel coronavirus in Iran, Preprint (Version 1).Research square. 2020.
6. Papoulis, Athanasios P, Pillai S. probability, random variables, and stochastic processe. 4th ed. Boston: McGraw-Hill. 2002.
7. Johnson NL, Kotz S, Balakrishnan N. Quot;14: lognormal distribution & quot; continuous univariate distributions. Wiley series in probability and mathematical statistics: applied probability and statistics. 2nd edn. John Wiley & Sons, NewYork. 1994:(1).
8. Hiteshi Tandon, Prabhat Ranjan, Tanmoy Chakraborty, et al. Coronavirus (COVID-19): ARIMA based time-series analysis to forecast near future. Quantitative Biology: Population and Amp; Evolution. 2020.
9. Alan P. Forecasting with univariate COVID-2019 epidemic dataset. Data in Brief. 2020:29.
10. Ikughur, Atsua Jonathan, Uba Tersoo, et al. Application of residual analysis in time series model selection. Journal of Statistical and Econometric Methods. 2009;4(4):41–53.
11. Domenico B, Marta G, Lazzaro V, et al. Application of the ARIMA model on the COVID-19 epidemic dataset. Data in Breif. 2015;29:105340..