The proportional hazard (PH) is commonly assumed for claiming efficacy and planning sample size in randomized clinical trials with time-to-event (TTE) type of endpoints. It is well known that the log-rank test is the most powerful testing method when the PH assumption holds. In recent years, with the advancement of immuno-oncology therapies, the non-PH scenarios, such as the delayed treatment effect and the diminished treatment effect, are frequently observed. A variety of alternative methods have been proposed for testing the time-to-event data while there is no uniformly most powerful method under the non-PH setting. In this paper, six popularly used methods for testing the TTE ata are reviewed followed by a numerical comparison.

Keywords: time-to-event, proportional hazard, log-rank test, restricted mean survival time

In oncology randomized clinical trials, the time-to-event(TTE) type of endpoints such as progression-free survival (PFS) and overall survival(OS), are commonly used as the primary or key secondary endpoints for comparing the experimental treatment and active control/placebo. In practice, the proportional hazard (PH) is usually assumed to characterize the treatment benefit over time of TTE endpoints and calculate the required sample size. With the PH assumption, the hazard ratio (HR) between treatment arms is a constant over time, and the corresponding testing hypothesis is expressed as

$H_0\mathrm{<mo>:</mo>}\text{HR}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}=\mathrm{1,}{H}_1\mathrm{<mo>:</mo>}\text{HR}\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}=c\mathrm{,}$

where $c\mathrm{<mo><</mo>1}$ . Recently, it is observed that the PH assumption does not hold in clinical trials investigating the cancer immunotherapies. Instead, a variety of non-PH pattens, such as the delayed treatment effect and the diminished treatment effect (e.g. Nivolumab)^1,2 were observed.

It is well known that the log-rank test is most powerful when the PH assumption holds. However, when the PH assumption is violated, the log-rank test may yield suboptimal power when compared with other testing procedures.^3,4 Therefore, extensive research has been conducted to explore alternative methods for handling the non-PH scenarios. In literature, multiple alternative methods have been proposed. In this paper, we provide a review of six popularly used testing methods including the log-rank test,⁵ the weighted log-rank test,⁶ the optimal weighted log-rank test,⁷ the restricted mean survival time,⁸ the weighted Kaplan-Meier,⁹ and minimum P-value.^10,11

The log-rank test⁵ is the most popularly used methods for comparing two distributions of the TTE data. Its popularity is largely due to the fact that log-rank test is the most powerful test with PH assumption as the test statistic is essentially equivalent to the score test.^5,12 Also the sample size planning based on the asymptotic property of log-rank test is convenient. However, researchers have pointed out that the log-rank test may yield suboptimal testing power in many non-PH cases.⁴

The weighted log-rank test is a natural extension of the log-rank test in order to provide a more flexible test statistic for handling the non-PH cases. The log-rank test becomes a special case of weighted log-rank test if a constant weight function over time is adopted. The Fleming-Harrington family $L^{p\mathrm{,}q}$ ⁶ is the most popular approach to specify weight functions as it consists a variety of weight functions to tackle different types of non-PH cases. The weighted log-rank test can yield robust power if a proper weight function is applied. Otherwise, the test statistics may cause a severe power loss, such as applying $L^{\mathrm{1,0}}$ for the scenarios with delayed treatment effect.

Recently, Liu et al.,⁷ further explore the optimal weight for the weighted log-rank test. The optimal weight refers to the weight function that maximizes the testing power within the weighted log-rank test family. It is showed that with mild asymptotic assumptions, the optimal weight is expressed as

where ${\lambda }_0\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>,}{\lambda }_1\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>,}\lambda \mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}$ are the respective hazard functions of control arm, treatment arm, and overall population. When PH assumption holds, it is straightforward that the optimal weight becomes a constant and thus log-rank test is most powerful. The key challenge for implementing the OptLR is regarding the estimation of hazard functions over time. The simulation results in Lin et al.,¹⁰ show that the optimal weighted log-rank test yields robust performance when delayed treatment effect is present. It is not surprising as the close form of optimal weight function can be derived in this setting. However, for other non-PH cases, further research needs to be conducted.

In contrast to LR, WLR, and OptLR, which essentially estimate the difference of hazard functions, the RMST⁹ directly estimates the difference $D$ of two survival functions over a follow-up period . That is,

where $S_0\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}$ and $S_1\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}$ are survival functions of treatment arm and control arm, respectively. The use of RMST is favored by physicians as its estimate $D$ has a clear clinical interpretation. For example, if $D\mathrm{<mo>=</mo>3}$ month with $L\mathrm{<mo>=</mo>2}$ years, then its clinical interpretation is that subjects receiving treatment is expected to survive 3 months longer during the first 2 year of treatment. In the setting of non-PH, Huang & Kuan⁴ show by the numerical simulation that the RMST yields more robust power performance than the log-rank test if parameter is properly chosen. Furthermore, Tian et al.,¹³ show the power advantage of RMST over LR in certain non-PH scenarios theoretically.

The WKM (Pepe & Fleming⁹) is a extension of the RMST by imposing a weight function on the RMST test statistic. The WKM is motivated by the fact that the estimation of survival function $S\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}$ becomes unstable when $t$ gets close to $L$ due to the high censoring and event rate. The WKM test statistic is expressed as

where the weight function is recommended to be a function of non-censoring rate $C_0\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}$ ,⁹ such as

That is to say, more weight is given to the survival estimates where censoring rate is low. It is shown that the WKM works better than LR and RMST when the overall censoring is heavy based on the simulation.⁹

As there are no uniformly most powerful test for testing the non-PH data, a versatile testing method MinP is proposed by Karrison.¹¹ The test statistic of MinP is expressed as

To evaluate the numerical performance of the aforementioned methods, we perform numerical evaluation by simulation in different settings of PH and non-PH. Due to the nature of this review paper, we only include the following examples for illustration purpose. There are five scenarios considered as shown in Figure 1: 1. the PH; 2. the delayed treatment effect with a high cure rate; 3. the delayed treatment; 4. the diminished treatment effect 5. the diminished treatment effect with crossed survival curves. For each scenario, the total sample size is 300 with analysis performed when 200 events are observed. For simplicity, no censoring is considered in the simulation examples and therefore WKM performs the same as RMST. Each simulation is replicated 5,000 times. The details of simulation scenarios are described as follows, and the simulation performance of LR, WLR ($L^{(0,1)}\mathrm{,}{L}^{(1,0)}$), OptLR, RMST, MinP are summarized in Table 1.

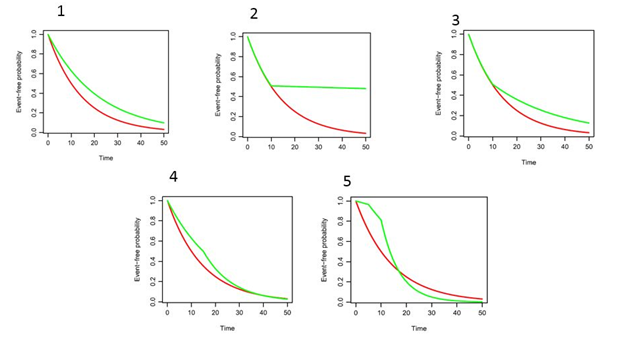
Figure 1 Simulation examples.

The control arm of each scenario follows exponential distribution with median survival 10 months. The Scenario 0 evaluates the performance of Type 1 error by setting the survival distribution of treatment arm in the same way.

1. For the Scenario 1, the treatment arm follows exponential distribution with hazard ratio (HR) 0.67.
2. For the Scenario 2, the treatment arm follows piecewise exponential distribution with otherwise.
3. For the Scenario 3, the treatment arm follows piecewise exponential distribution with $HR{}_1=\mathrm{1,}t\mathrm{<mo><</mo>}10\mathrm{<mo>;</mo>}HR{}_2=0.5\mathrm{,}$ otherwise.
4. For the Scenario 4, the treatment arm follows piecewise exponential distribution with$HR{}_1=\mathrm{0.67,}t\mathrm{<mo><</mo>}15\mathrm{<mo>;</mo>}HR{}_2=\mathrm{1.2,}$ otherwise.
5. For the Scenario 5, the treatment arm follows piecewise exponential distribution with $HR{}_1=\mathrm{0.1,}t<5\mathrm{<mo>;</mo>}HR{}_2=\mathrm{0.5,5}\le t<10\mathrm{<mo>;</mo>}HR{}_3=2$ otherwise.

From Table 1, it is evident that all the methods preserve the Type 1 error strictly. The LR yields robust performance when the PH holds while a significant power loss is observed in multiple non-PH settings. The performance of WLR depends on the selection of weight functions, which is difficult to be properly pre-specified. The RMST performs similarly as LR, and its estimate has straightforward clinical interpretation. The OptLR and MinP yield strong performance in all scenarios. It worths noting that the good performance of OptLR could be due to the fact that the optimal weights in the simulation examples are easy to estimate.

As illustrated in Section 2, a rich set of methods has been available for testing TTE data. However, there is no uniformly most powerful method in the non-PH setting. Therefore, it is important to conduct intensive numerical evaluation for understanding the operating characterics of different methods before decision making. Otherwise, a significant power loss could be caused due to the selection of testing method. Furthermore, the numerical evaluation needs to carefully designed via reviewing the historical data and the mechanism of action of investigational drug. For instance, the numerical evaluation for immuno-oncology compounds may focus on the delayed effect scenarios. For the further work, the theoretical development on comparing the efficacy of existing methods as Tian at al.,¹³ and the software development to facilitate the use of existing methods, such as R Shiny, could be interesting.

None.

Authors declare that there is no conflicts of interest.

1. Ferris R, George B, Blumenschein, et al. Nivolumab for recurrent squamous–cell carcinoma of the head and neck. The New England Journal of Medicine. 2016;375:1856–1867.
2. Carbone D, Martin R, Luis P, et al. First–line nivolumab in stage IV or recurrent non–small–cell lung cancer. The New England Journal of Medicine. 2017;376:2415–2426.
3. Xu Z, Zhen B, Park Y, et al. Designing therapeutic cancer vaccine trials with delayed treatment effect. Statistics in Medicine. 2017;36:592–605.
4. Huang B, Kuan P. Comparison of the restricted mean survival time with the hazard ratio in superiority trials with a time–to–event endpoint. Pharmaceutical Statistics. 2018;17(3):202–213.
5. Peto R, Peto J. Asymptotically efficient rank invariant test procedures. Journal of the Royal Statistics Society, Series A. 1972;135:185–207.
6. Harrington D, Fleming T. A class of rank test procedures for censored survival data. Biometrika. 1982;69:553–566.
7. Liu S, Chu C, Rong A. Weighted log–rank test for time–to–event data in immunotherapy trials with random delayed treatment effect and cure rate. Pharmaceutical Statistics. 2018;17(5):541–554.
8. Karrison T. Restricted mean life with adjustment for covariate. Journal of the American Statistical Association. 1987;82:1169–1175.
9. Pepe M, Fleming T. Weighted Kaplan–Meier statistics:a class of distance tests for censored survival data. Biometrics. 1989;45:497–507.
10. Lin Y, Zhou K, Ganju J. A single test for rejecting the null hypothesis in subgroups and in the overall sample. Journal of Biopharmaceutical Statistics. 2017;27(1):101–110.
11. Karrison T. Versatile tests for comparing survival curves based on weighted log–rank statistics. Stata Journal. 2016;16:678–690.
12. Strawderman R. An asymptotic analysis of the logrank test. Lifetime Data Analysis. 1997;3(3):225–249.
13. Tian L, Fu H, Ruberg S, et al. Efficiency of two sample tests via the restricted mean survival time for analyzing event time observations. Biometrics. 2017;74:694–702.