
Research Article Volume 7 Issue 1
A discrete lindley distribution with applications in biological sciences
Berhane Abebe, Rama Shanker
Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Department of Statistics, College of Science, Eritrea Institute of Technology, Eritrea
Correspondence: Rama Shanker, Department of Statistics, College of Science, Eritrea Institute of Technology, Asmara, Eritrea
Received: January 24, 2018 | Published: February 9, 2018
Citation: Abebe B, Shanker R. A discrete lindley distribution with applications in biological sciences. Biom Biostat Int J. 2018;7(1):48-52. DOI: 10.15406/bbij.2018.07.00189
Download PDF
Abstract
In this paper, a discrete Lindley distribution, a discrete analogue of continuous Lindley distribution using infinite series method of discretization, has been proposed and investigated. Its generating functions, moments and moments based measures including coefficients of variation, skewness, kurtosis, index of dispersion have been obtained and discussed. Both the method of moments and the method of maximum likelihood estimation have been discussed for estimating its parameter. Applications of the proposed distribution have been explained through two examples of observed real datasets from biological sciences.
Keywords: lindley distribution, discretization, moment generating function, moments, estimation, goodness of fit
Introduction
In the last few decades many papers appeared in the statistical literature on the discretization of continuous distributions. The main reasons for discretizing a continuous distributions are two fold, namely, (i) the discrete analogue of a continuous distribution provide probability mass function (pmf) that can compete with the classical discrete distributions commonly used in the statistical analysis of count data and (ii) the discrete analogue of a continuous distribution avoids the use of a continuous distribution in the case of strictly discrete data.
According to Lai,1 discretization of a continuous lifetime model is an interesting and intuitively appealing approach to derive a discrete lifetime model corresponding to the continuous one. It has been observed that many times in the real world the original variables may be continuous in nature but discrete by observation and , therefore, it is reasonable and convenient to model the situation by an appropriate discrete distribution generated from the underlying continuous distribution preserving one or more important characteristics including probability density function (pdf), moment generating function (mgf), moments, hazard rate function, mean residual life function etc., of the continuous distribution.
There are several methods available in Statistics literature to derive a discrete distribution from a continuous distribution. One of the first proposed discretization methods is based on the definition of pmf that depends on an infinite series. The method of discretization by an infinite series was firstly considered by Good2 who has proposed the discrete Good distribution to model the population frequencies of species and the estimation of parameters. A random variable
is said to have a discrete Good distribution if its pmf can be expressed as
(1.1)
The method of infinite series is characterized by the following definition
Definition 1.1: Let
be a continuous random variable having pdf
with support on. Then the corresponding discrete random variable
has pmf given by
(1.2)
where
may be the vector of parameters indexing the distribution of
.
This method of discretizing a continuous distribution has been studied by several researchers including Kulasekara and Tonkyn,3 Doray and Luong,4 Sato et al.,5 Nekoukhou et al.,6 are some among others, who proposed a version of the method when the continuous random variable of interest is defined
on. Thus, if the random variable
is defined on
, the pmf of
can be defined as
(1.3)
Note that the discrete distribution generated using the method of infinite series may not always have a compact form due to the normalizing constant.
In the present paper, a discrete Lindley distribution (DLD), a discrete analogue of continuous Lindley distribution proposed by Lindlley7 has been introduced using a discretization method based on an infinite series. Its moment generating function, moments and moments based measures have been obtained and discussed. Both the method of moment and the method of maximum likelihood estimates give the same estimator of the parameter of DLD. The applications and the goodness of fit of the proposed distribution have been explained using two real datasets from biological sciences and the fit has been compared with other discrete distributions.
A Discrete lindley distribution
The pdf and the cdf of a continuous random variable
having Lindley distribution introduced by Lindlley7 are given by
(2.1)
(2.2)
Ghitany et al.,8 has discussed its various mathematical and statistical properties including its shapes for varying values of parameter, moments based measures, hazard rate function, mean residual life function, stochastic ordering, mean deviations,
order statistics, Renyi entropy measure, Bonferroni and Lorenz curves and stress-strength reliability along with estimation of parameter and application for modeling waiting time in a bank. Shanker et al.,9 have detailed comparative study
on applications of Lindley distribution and exponential distribution for modeling lifetime data and observed that both distributions are competitor to each other for modeling lifetime data from various fields of knowledge. In fact, in some datasets
exponential distribution gives much closer fit than the Lindley distribution and in some datasets Lindley distribution gives better fit than exponential distribution.
Using the definition (1.1), the pmf of the discrete random variable
corresponding to a continuous random variable X following Lindley distribution (2.1) can be obtained as
(2.3)
We would call this distribution, a discrete Lindley distribution (DLD). The nature and behavior of DLD for varying values of its parameter
has been shown graphically in figure 1.
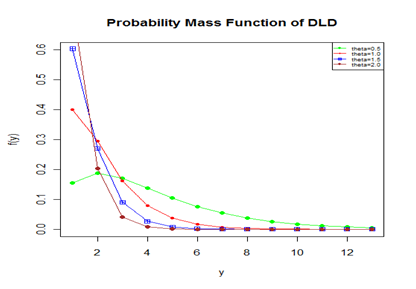
Figure 1 The pmf plot of DLD for varying values of the parameter
.
The survival function
,and the cumulative distribution function (cdf),
of DLD can be obtained as
(2.4)
(2.5)
Graph of cumulative distribution function of DLD for varying values of its parameter
has been shown in figure 2.
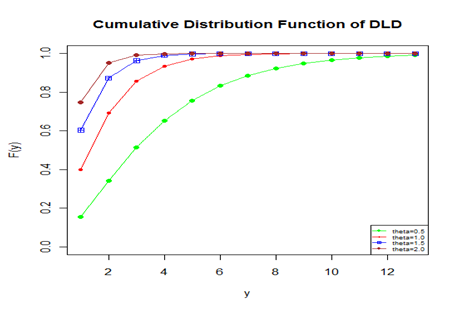
Figure 2 The cdf plot of DLD for varying values of the parameter
.
Since
is a decreasing function of
,
is log-concave and therefore, the DLD has an increasing hazard rate. Further,
for
, which implies unimodality, by theorem 3 of Keilson and Gerber.10 The interrelationship between log-concavity, unimodality
and increasing hazard rate of discrete distributions are available in Grandell.11
Moments, skewness, kurtosis and index of dispersion
The probability generating function (G(t)) and the moment generating function (M(t)) of DLD can be obtained as
(3.1)
and
(3.2)
It can be easily verified that the function in (3.2) is infinitely differentiable with respect to
, since it involves exponential terms of its argument. This means that all moments about origin
of DLD can be obtained. The first four moments about
origin of DLD can thus be obtained as
Using the relationship
between central moments and moments about origin, the central moments of DLD are obtained as
The expressions for coefficient of variation (C.V), coefficient of skewness
, coefficient of kurtosis
and index of dispersion
of DLD are expressed as
.
Since
always for
, a DLD is over dispersed
. This means that DLD can be used to model over-dispersed data from any fields of knowledge.
Table 1 summarizes the nature and behavior of coefficient of variation (C.V), coefficient of skewness, coefficient of kurtosis and index of dispersion (ID) of DLD for selected values of the parameter
.
|
Values of descriptive statistics |
Mean |
Variance |
C.V |
Skewness |
Kurtosis |
ID |
0.5 |
3.0380 |
7.8354 |
0.9079 |
1.4586 |
6.1276 |
2.5415 |
1 |
1.6400 |
1.8413 |
1.1658 |
1.5947 |
6.5431 |
1.5820 |
1.5 |
0.5744 |
0.7394 |
1.4969 |
1.8310 |
7.3524 |
1.2872 |
2 |
0.3131 |
0.3620 |
1.9221 |
2.1822 |
8.7622 |
1.1565 |
2.5 |
0.1789 |
0.1948 |
2.4680 |
2.6706 |
11.1323 |
1.0894 |
3 |
0.1048 |
0.1103 |
3.1690 |
3.3268 |
15.0677 |
1.0524 |
3.5 |
0.0623 |
0.0642 |
4.0691 |
4.1920 |
21.5728 |
1.0314 |
4 |
0.0373 |
0.0380 |
5.2248 |
5.3205 |
32.3082 |
1.0187 |
Table 1 Values of descriptive statistics of DLD for varying values of parameter
It is obvious from above table that the mean, variance, and index of dispersion of DLD are decreasing for increasing values of the parameter
, while coefficient of variation, coefficient of skewness and coefficient of kurtosis of DLD are increasing for
increasing values of parameter
. Since
, DLD is a suitable model for over-dispersed data.
Parameter estimation
Method of moment estimate (MOME): Equating the population mean to the corresponding sample mean, the MOME
of
of DLD is given by
, where
is the sample mean.
maximum likelihood estimate (MLE): Let
be a random sample from DLD (2.3)). The likelihood function,
of (2.3) is given by
.
The natural log likelihood function is thus obtained as
The maximum likelihood estimates (MLE)
of parameter
is the solution of the log-likelihood equation
and is given by
.
This means that both MOME and MLE give the same estimator for the parameter
.
Goodness of fit
As we have seen that DLD is over-dispersed and hence it can be applied to model over-dispersed data. In general, the discrete data in biological sciences are over-dispersed and due to this we have taken two examples of observed real datasets from biological
sciences. The first dataset is the data regarding number of Homocytometer yeast cell counts per square, available in Gosset.12 The second dataset is the data regarding the number of European corn borer available in Mc Guire et al.,13 The goodness of fit of DLD has been compared with one parameter Poisson distribution (PD) which is equi-dispersed and Poisson-Lindley distribution (PLD) which is over-dispersed and proposed by Sankaran14 as a Poisson mixture of Lindley
distribution, introduced by Lindley.7 It should be noted that Shanker and Hagos15 has detailed study on applications of PLD in biological sciences and observed that for biological sciences data, PLD is the appropriate choice
(Table 2&3).
Number of red mites |
Observed |
Expected frequency |
|
frequency |
PD |
PLD |
DLD |
0 |
213 |
202.10 |
234.00 |
222.35 |
1 |
128 |
138.00 |
99.40 |
113.14 |
2 |
37 |
47.10 |
40.50 |
43.18 |
3 |
18 |
10.70 |
16.00 |
14.65 |
4 |
3 |
1.80 |
6.20 |
4.66 |
5 |
1 |
0.20 |
2.40 |
1.42 |
6 |
0 |
0.10 |
1.50 |
0.59 |
Total |
400 |
400.00 |
400.00 |
400.00 |
ML Estimate |
|
0.6825 |
1.9502 |
1.3687 |
|
|
10.0900 |
11.0610 |
3.2511 |
d.f. |
|
2 |
2 |
2 |
p-value |
|
0.0178 |
0.0114 |
0.3545 |
Table 2 Observed and expected number of homocytometer yeast cell counts per square observed by gosset12
Number of European corn-borer |
Observed
frequency |
Expected frequency |
PD |
PLD |
DLD |
0 |
188 |
169.40 |
194.00 |
184.80 |
1 |
83 |
109.80 |
79.50 |
90.47 |
2 |
36 |
35.60 |
31.30 |
33.24 |
3 |
14 |
7.80 |
12.00 |
10.84 |
4 |
2 |
1.20 |
4.50 |
3.32 |
5 |
1 |
0.20 |
2.70 |
1.36 |
Total |
324 |
324.00 |
324.00 |
324.00 |
ML Estimate |
|
0.6481 |
2.0425 |
1.4075 |
|
|
15.2000 |
1.2970 |
1.0425 |
d.f. |
|
2 |
2 |
2 |
p-value |
|
0.0040 |
0.7297 |
0.7910 |
Table 3 Observed and expected number of European corn-borer of McGuire et al13
It is obvious from the values of chi-square that DLD gives much closer fit than both PD and PLD, and hence DLD can be considered an important discrete distribution for modeling discrete data in biological sciences.
Conclusions
In this paper, a discrete Lindley distribution (DLD), a discrete analogue of continuous Lindley distribution, has been proposed and investigated. Its moment generating function, moments and moments based measures including coefficients of variation, skewness,
kurtosis, and index of dispersion have been obtained and their nature have been discussed numerically. Both the method of moments and the method of maximum likelihood estimation have been discussed for estimating its parameter. The applications of
DLD have been discussed with two examples of observed real datasets from biological sciences. The DLD gives much closer fit over Poisson distribution (PD) and Poisson Lindley distribution (PLD).
Acknowledgements
None.
Conflicts of interest
None.
References
- Lai CD. Issues concerning constructions of discrete lifetime models. Qual Techno Quant Mang. 2013;10(2):251‒262.
- Good LJ. The population frequencies of species and the estimation of population parameters. Biometrika. 1953;40:237‒264.
- Kulasekara KB, Tonkyn DW. A new discrete distribution with application to survival, dispersal and dispersion. Commun Stat Simul Comput. 1992;21:499‒518.
- Doray LG, Luong A. Efficient estimator s for the Good family. Commun Stat Simul Comput. 1997;21:499‒518.
- Sato H, Ikota M, Aritoshi S. A new defect distribution in meteorology with a consistent discrete exponential formula and its applications. IEEE Trans Semicond Manufactur. 1999;12(4):409‒418.
- Nekoukhou VM, Alamatsaz MH, Bidram H. Discrete Generalized exponential distribution. Communications in Statistics-Theory & Methods. 2012;41:2000‒2013.
- Lindley DV. Fiducial distributions and Bayes’ theorem. Journal of the Royal Statistical Society. Series B. 1958;20:102‒107.
- Ghitany ME, Atieh B, Nadarajah S. Lindley distribution and its Application. Mathematics Computing and Simulation. 2008;78:493‒506.
- Shanker R, Hagos F, Sujatha S. On Modeling of Lifetimes data using Exponential and Lindley distributions. Biometrics & Biostatistics International Journal. 2015;2(5):1‒9.
- Keilson J, Gerber H. Some resilts for Discrete Unimodality, Journal of the American Statistical Association 1971;66:386‒389.
- Grandell J. Mixed Poisson Processes, CRC Press. 1997.
- Gosset WS. The probable error of the mean. Biometrika. 1908;6(1):1‒25.
- Mc Guire JU, Brindley TA, Bancroft TA. The distribution of European corn-borer larvae pyrausta in field corn. Biometrics. 1957;13:65‒78.
- Sankaran M. The discrete Poisson-Lindley distribution. Biometrics. 1970;26:145‒149.
- Shanker R, Hagos F. On Poisson-Lindley distribution and its Applications to Biological Sciences. Biometrics & Biostatistics International Journal. 2015;2(4):1‒5.

©2018 Abebe, et al. This is an open access article distributed under the terms of the,
which
permits unrestricted use, distribution, and build upon your work non-commercially.


