
Correspondence:
Received: January 01, 1970 | Published: ,
Citation: DOI:
Download PDF
Abstract
The influence of constant and periodic external fields on the living systems can lead to various changes in their functional properties. At the molecular level, these changes can be modeled as the changes in the dynamic properties of biomolecules. In this paper we investigate the effect of constant and periodic fields on the movement of transcription bubbles being small unwound regions (~10bp) in the DNA double helix, which result from the interaction of the RNA polymerase with the DNA promoter region at the initiation stage of the process of transcription. The bubbles are modeled mathematically by kinks being one–soliton solutions of the modified sine–Gordon equation. To obtain these solutions and calculate the dynamic characteristics of the bubbles including their velocity, coordinate, phase portrait, total energy and size, we apply the method of McLaughlin and Scott and quasi–homogeneous approximation. For definiteness all of the calculations were made for the pTTQ18 sequence. The results were used to analyze the bubbles dynamic behavior and to answer the question: is it possible to govern the movement of the transcription bubbles of DNA by constant and periodic external fields? Possible consequences on the gene expression and biological activity of cells are discussed.
Keywords: transcription bubble, DNA torque, periodic fields, sine–Gordon equation, method of McLaughlin and Scott, quasi–homogeneous approximation, nonlinear DNA dynamics
Abbreviations
DNA, deoxyribo nucleic acid; AOT, angular optical trap; MTT, magnetic tweezers technique
Introduction
The action of constant and periodic fields on the living systems is one of the hotly discussed themes of modern biophysics because of the growing amount and variety of electronic devices and their influence on the basic, fundamental life processes and, consequently, on human health. It is assumed, in particular, that external periodic fields with the frequency of terahertz diapason can cause the changes in the physicochemical properties of DNA, which in turn can lead to the changes in the transcription and thus to the changes in the gene expression and cell differentiation.1,2 However, until now the mechanisms of the action of these fields remain unclear. Special attention is also paid to the influence of constant fields because of significant progress in the experimental studies of the dynamics of single molecules of DNA and by the development of new techniques that allows to measure directly the DNA torque.3 The method of the angular optical trap (AOT)4,5 and the method of magnetic tweezers technique (MTT)6–8 are among them. However, these and other currently existing experimental methods do not allow measure the DNA torque directly in the biological processes in which the DNA molecule is involved.
In this paper we apply the methods of mathematical modeling to investigate the action of constant and periodic fields on the movement of transcription bubbles of DNA which are small unwound regions (~10bp) in the DNA double helix resulting from the interaction of the RNA polymerase with the DNA promoter region at the initiation stage of the process of transcription (Figure 1).9 Our aim is to clarify the mechanisms of the influence of the fields on the bubbles dynamics, to find the relationship between the DNA torque and the bubble velocity, to estimate the value of the DNA torque necessary for the moving of the bubbles with the velocity of the process of transcription, to find the relation between the dynamic behavior of the bubbles and their initial velocities, and to give an answer to the question is it possible to govern the movement of the transcription bubbles of DNA by constant and periodic external fields (Figure 1).
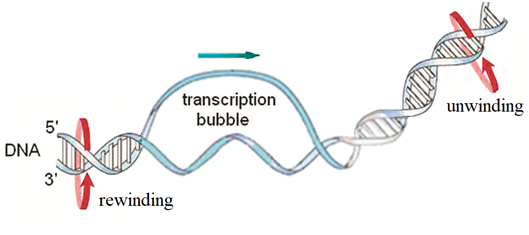
Figure 1 Locally unwound region (bubble) in the DNA double strand, which is formed at the initial stage of transcription.
In physics, the DNA molecule is considered as a complex dynamic system consisting of a large number of coupled atoms and atomic groups which are arranged in a certain way in space. Such a system is not static, but movable. It has a large amount of internal motions caused by the effect of temperature, collisions with the molecules of the solution, and interactions with proteins. Among the variety of the internal motions of DNA there are the translational movements of transcription bubbles that can be considered as translational movements of quasi–particles in the potential field of the DNA.
Mathematically the transcription bubbles can be described as the soliton–like solutions of the nonlinear differential equations imitating the internal DNA mobility. In the case of homogeneous synthetic DNA having the sequence of identical bases, Englander and co–authors10 showed that the bubble movement can be modeled by the sine–Gordon equation with constant coefficients, this equation having the exact one–soliton solutions in the form of kinks. In the work of Englander and co–authors10 as well as in the works of other authors developing the Englander’s idea,11–20 just these solutions were used to simulate the DNA open states or bubbles. To take into account effects of dissipation and the action of some external field, they modified the sine–Gordon equation by adding the following two terms: one to model effect of dissipation and the other to model influence of an external field. With the help of the method of McLaughlin and Scott21 the kink–like solutions of the modified sine–Gordon equation were found in the two particular cases: when the external field is constant and when the external field is periodic.22,23
In the case of inhomogeneous DNA, the coefficients of the modified sine–Gordon equation are no longer constants, but depend on the sequence of bases (Table 1). However, in the quasi–homogeneous approximation, this equation can be reduced to the homogeneous one but with the changed coefficients the values of which depend on the concentrations of different types of bases. In this paper we apply the quasi–homogeneous approximation to solve the equation of that type and to calculate the main dynamic characteristics of the bubbles necessary to analyze the influence of constant and periodical fields on the bubble behavior.
For definiteness we take a sequence of small circular DNA molecule–plasmid pTTQ18 (Figure 2) which is widely used in genetic engineering to transfer genetic information and for genetic manipulations.24 The plasmid sequence contains four functionally important regions: promoter (54–333), terminator (611–8011), and two coding regions CDS–1 (1585–2544) and CDS–2 (2762–3622). The sequence length is 4563 bases. Of these, the sequence has 1105 adenines, 1090 thymines, 1193 guanines and 1175 cytosines. In the second section, we describe the model and methods used. In the further two sections the results on the velocity, coordinate, phase portrait, total energy and size of the bubbles moving under the action of the constant and periodic fields are presented. In the final section the obtained results are discussed and the main conclusions are made (Figure 2).
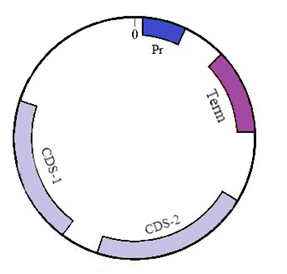
Figure 2 Schematic picture of plasmid pTTQ18. Four functional areas are shown: promoter (Pr), terminator (Term) and two coding regions (CDS-1, CDS-2).
Models and methods
Let us begin with the discrete version of the modified sine–Gordon equation:25
(1)
Here is the angular displacement of the n–th base, is the moment of inertia of the n–th base, is the stiffness of the sugar–phosphate chain,is the distance between adjacent base pairs, is the factor characterizing the interaction between the complementary bases inside the n–th pair, n = 1, 2, ... N, N is the number of bases in the sequence, , is the dissipation factor, is the constant torque, is a periodic field.
The values of the coefficients in the left side of the system of equations (1) are shown in Table 1. The values of the parameters of the external fields (, and ) are yet arbitrary.
Type of the
n-th base |
(10-44 kg×m2) |
(J/m2) |
(10-10 m) |
(10-20 J) |
(10-10 m) |
(J×с) |
adenine |
7.61 |
6.75 |
5.8 |
2.09 |
3.4 |
4.25 |
thymine |
4.86 |
6.75 |
4.8 |
1.43 |
3.4 |
2.91 |
guanine |
8.22 |
6.75 |
5.7 |
3.12 |
3.4 |
4.10 |
cytosine |
4.11 |
6.75 |
4.7 |
2.12 |
3.4 |
2.79 |
Table 1 Coefficients of Eq. (1)25,26
Let us assume that the desired solutions of Eqs. (1) are sufficiently smooth functions. Then, we can apply the continuum approximation:
, ,
,
, ,
, .
As a result Eqs. (1) are transformed to:
(2)
To simplify further calculations, we use the quasi–homogeneous approximation according to which we can replace the coefficients of the left–hand side of Eq. (2) by the averaged values:27
,
, (3)
,
,
where is the number of adenines, is the number of thymines, is the number of guanines, is the number of cytosines, and is the total number of bases in the sequence.
After the averaging procedure, Eq. (2) takes the form similar to the sine–Gordon equation, but with the coefficients recalculated by formulas (3):
, (4)
where . Numerical values of the coefficients that are averaged over the entire sequence of plasmid pTTQ18 are given in Table 2.
Type of the sequence |
(10-44 kg×m2) |
(10-18 J) |
(10-20 J)
|
(10-34 J×c) |
pTTQ18 |
6.21 |
1.88 |
2.21 |
3.51 |
Table 2 Coefficients of Eq. (4)
For convenience, let us introduce new (dimensionless) variables:
, , where , . In these variables, Eq. (4) takes the form:
, (5)
where , , ,.
If the dimensionless coefficient of dissipation is small (), Eq. (5) has approximate one–soliton solution in the form of kink:
(6)
The velocity of which is defined by the equation of McLaughlin and Scott:21
(7)
Here , is an arbitrary constant.
Let us determine the coordinates of the kink x by formula:
, (8)
and the total energy and the size of the kink by the formulas:
, . (9)
Differentiating (9) with respect to , we get two additional differential equations:
, (10)
. (11)
Eqs. (7), (8) and (10), (11) are a complete set of equations which are necessary to calculate the time dependencies of the velocity, coordinate, size and total energy of the transcription bubbles.
Results and discussion
Here we present the results of numerical calculations of the velocity, coordinate, size and total energy of the transcription bubbles. To better understand the dynamic behavior of the bubbles, we made for three different values of the external torsion moment and for three different values of the initial velocities of the bubbles.
Bubbles dynamics under the action of constant external field
This case corresponds to ,. Dynamic characteristics of the bubbles, obtained for three different values of the torsion moment , are shown in Figure 3A & 3B. The bubbles trajectories in the phase plane () are shown in Figure 3C. The bubble total energy and size are shown in Figures 3D & 3E. The time required for calculation of the curves in Figures 3A &3B and of the curve 1 in Figure 3(C), is equal to 2.5×103. The time required for calculation of the curves 2 and 3 in Figure 3C is equal to 5×103 and 5×104, respectively (Figure 3).
The values and are chosen arbitrarily. The value is assumed to be equal to which in turn is determined from Eq. (7) at :
(12)
From Figure 3A it is seen that at (curve 2) the bubble velocity is constant and equal to the initial velocity. At (curve 3), the bubble kink velocity initially decreases and after a time period (T), equal approximately 500 (0.84ns), reaches the stationary value:
(13)
At (curve 1), the kink velocity initially increases and after approximately the same time period T, reaches the stationary value:
(14)
From Figure 3B it is seen that at (line2) the bubble coordinate is a completely straight line. At (curve 3), the coordinate initially forms a small bend, and then after a certain period of time it transforms into a straight line. Similarly, at (curve 1), the coordinate initially forms a small bend (in opposing direction), and then it also transforms into a straight line.
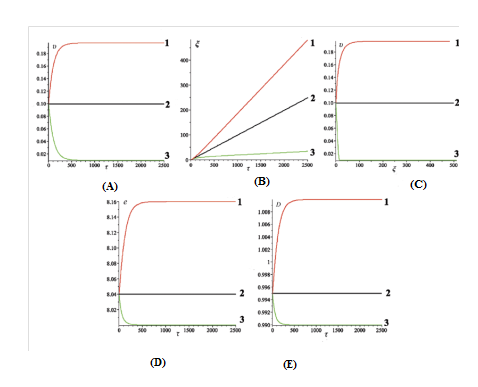
Figure 3 (A) Velocity
, (B) coordinate
, (C) phase trajectory, (D) total energy
and (E) size
of the transcription bubble. The curves with number 1 correspond to . The lines with number 2 correspond to
. The curves with number 3 correspond to
. Initial bubble velocity
. Dissipation factor
.
From Figures 3D & 3E it is seen that at (curve 2) the bubble energy and size are constants. At (curves with number 3), the bubble energy before reaching the stationary value is reduced from the value , and the bubble size is reduced from till . At (curves with number 1), the bubble energy before reaching the stationary value is increased from the value till the value , and the bubble size is increased from till . Hence, by setting different values of constant external torsion field we can force the bubble to move with a certain fixed velocity. The opposite is true. If we know that bubble is moving at a given velocity, we can calculate the value of the torsion moment, which will ensure the movement of bubble at that velocity.
The above studies make it possible to estimate the value of the constant torsion moment , necessary for the movement of the transcription bubble at the velocity equal to the velocity of the process of transcription. To do this, we replace in formula (13) with the transcription velocity and replace the constant field with the value . As a result, we obtain the ratio between the transcription velocity and the sought value of the constant external field:
(15)
We rewrite the formula (15) in dimensional variables:
(16)
where is the dimensional transcription velocity, is the unknown constant external field, is the sound velocity in the plasmid pTTQ18. From (16) we find the sought torsion moment :
(17)
If we assume that the velocity of transcription is equal to 100 base pairs per second , then from formula (17) we find the desired estimate: Figure 4 shows the results of numerical calculations of the dynamic characteristics of the bubbles, made for three different values of the initial velocity (Figure 4).
Figure 4A shows that for any value of the initial bubble velocity the values of stationary velocity are the same. Figure 4B shows that the slopes of the bubbles trajectories reach the same value. Figure 4C & 4D shows that for different values of initial velocities the bubbles energy and size also reach the same values. Thus, we can conclude that the stationary dynamic characteristics of the bubbles do not depend on the initial velocities. On the contrary, they depend only on the value of the torsion moment.

Figure 4 (a) Velocity
, (b) coordinate
, (c) phase trajectory, (d) total energy
and (e) size
of the transcription bubble. Initial velocities:
,
,
. Torsion moment
. Dissipation factor
.
Bubbles dynamics under the action of periodic external field
This case corresponds to,,. It could be realized, for example, in an experiment with a single molecule at the work of atomic force microscope in an oscillating manner.28 Figure 5A–5C show the dynamic characteristics of the bubbles, obtained for three different values of the amplitude of the external periodic field (Figure 5).
Analyzing the graphs of coordinate and velocity presented in Figure 5A & 5B one can notice that at the beginning of the bubbles movement there exists a short period where oscillations are establishing. After the end of the period T the bubbles continues to oscillate with the constant frequency . Figure 5D & 5E show the time dependence of the total energy and the size of the bubbles. It can be seen the doubling of the frequency of the stationary oscillations. Figure 6 shows the dynamic characteristics of the bubbles, obtained for three different values of the initial velocity: ,,(Figure 6).
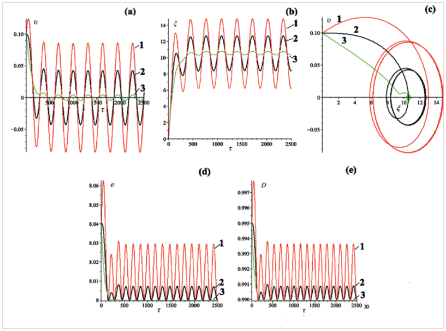
Figure 5 (a) Velocity
, (b) coordinate
, (c) phase portrait, (d) total energy
and (e) size
of the kink. The curves with number 1 correspond to
. The curves with number 2 correspond to
, the curves with number 3 correspond to
. Frequency
. Initial bubble velocity
.
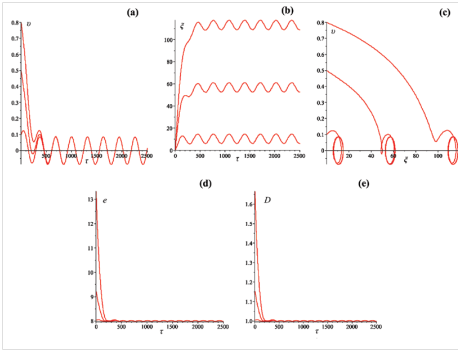
Figure 6 (a) Velocity
, (b) coordinate
, (c) phase portrait, (d) total energy
and (e) size
of the bubble. Initial velocities:
,
,
. Amplitude
. Frequency
. Dissipation factor
.
From Figure 6 it is seen that after some short period the velocity and coordinate of the bubbles having different initial velocities at the "start–up, begin to oscillate with constant amplitude and frequency. It can be seen also the doubling of the frequency of the oscillations of the bubbles energy and size.
Conclusion
Transcription bubbles have been modeled as quasi–particles – kinks, moving in the potential field of DNA. The influence of constant and periodic fields on the movement of the kinks was studied by the method McLaughlin and Scott. The time dependences of the kinks velocity, coordinate, total energy and size were obtained.
When calculating we used the following dimensionless values of the initial bubbles velocity: , , . In the dimensional units these values correspond to: m/s, m/s, m/s. To model the constant torsion moment, we used the dimensionless values: , , , corresponding to the dimensional values: J, J, J. To simulate the amplitude and frequency of the periodic external field, we used dimensionless values: , , , , corresponding to the dimensional values: J, J, J, s–1.
It was shown that in the case of constant torque, there is a small time period (0.84 ns), after which the bubble velocity reaches the stationary value. This stationary value does not depend on the initial bubble velocity and is completely determined by the value of constant torque. By setting this or that value of the constant torsion moment we can force the bubble to move at a predetermined velocity. We used this result to estimate theoretically the value of the DNA torque which can not be measured by currently existing experimental methods. We obtained that this value is equal to 0.49∙10–31 J if the velocity of transcription process is equal to 100 base pairs per second. Moreover we derived formula relating DNA torque and the velocity of transcription.
It was also shown that in the case of periodic field there is almost the same time period after which the bubble begins to oscillate with constant amplitude and frequency the value of which does not depend on the initial bubble velocity. This can lead to the destruction of the transcription bubble.
It is necessary to note, however, that all these results has been obtained in the frameworks of a rather simple model, which simulates angular oscillations of nitrous bases in one of the two polynucleotide chains, the other chain being modeled as an averaged external field. But we expect that further improvement of the model due to taking into account the transverse and longitudinal displacements of nitrous bases, the mobility of bases in the other polynucleotide chain, the helicity of the DNA structure will not change the main conclusions about the role of the constant and the periodic field in the bubble dynamics
Acknowledgements
The authors thank Dr. Dana Flavin for the valuable discussions which helped to broaden and deepen our understanding of the importance of the considered problems and its relationship to the fundamental problems of vital activity and human health.
Conflict of interest
Author declares that there is no conflict of interest.
References
- Alexandrov BS, Gelev V, Bishop AR, et al. DNA Breathing Dynamics in the Presence of a Terahertz Field. Phys Lett. 2010;374(10):1214–1217.
- Alexandrov BS, Gelev V, Yoo SW, et al.DNA Dynamics Play a Role as a Basal Transcription Factor in the Positioning and Regulation of Gene Transcription Initiation. Nucleic Acids Res. 2010;38(6):1790–1795.
- Severin ES. Biochemistry. Moscow: GEOTAR–Media; 2016.
- Englander SW, Kallenbach NR, Heeger AJ, et al. Nature of the open state in long polynucleotide double helices:possibility of soliton excitations. Proc Natl Acad Sci U S A. 1980;77(12):7222–7226.
- Cuenda S, Sánchez A. Nonlinear excitations in DNA:Aperiodic models versus actual genome sequences. Phys Rev E. 2004;70(51):051903.
- Barbi M, Place C, Popkov V, et al. Base-sequence-dependent sliding of proteins on DNA. Phys Rev E. 2004;70(41):041901.
- Gaeta G. Solitons in the Yakushevich model of DNA beyond the contact approximation. Phys Rev E. 2006;74(2):021921.
- González JA, Cuenda S, Sánchez A. Kink dynamics in spatially inhomogeneous media:The role of internal modes. Phys Rev E. 2007;75(3):036611.
- Gaeta G, Venier L. Solitary waves in twist-opening models of DNA dynamics. Phys Rev E. 2008;78(1):011901.
- Cadoni M, De Leo R, Demelio S, et al. Propagation of twist solitons in real DNA chains. Journal of Nonlinear Mathematical Physics. 2010;17(4):557-569.
- Theodorakopoulos N. Melting of genomic DNA:predictive modeling by nonlinear lattice dynamics. Phys Rev E. 2010;82(2):021905.
- Cuenda S, Quintero NR, Sánchez A. Sine-Gordon wobbles through Bäcklund transformations. Discrete and Continuous Dynamical Systems. 2011;4(5):1047–1056.
- Derks G, Gaeta G. A minimal model of DNA dynamics in interaction with RNA-Polymerase. Physica D. 2011;240(22):1805–1817.
- Theodorakopoulos N. Peyrard M. Base pair openings and temperature dependence of DNA flexibility. Phys Rev Lett. 2012;108(7):078104.
- Forth S, Sheinin MY, Inman J, et al. Torque measurement at the single-molecule level. Annu Rev Biophys. 2013;42(1);583–604.
- Yakushevich LV, Balashova VN, Zakiryanov FK. O dvijenii kinka DNK pod deistviem postoyannogo torsionnogo momenta. Mathematical Biology and Bioinformatics. 2016;11(1):81–89.
- McLaughlin DW, Scott AC. Perturbation analysis of flu-xon dynamics. Phys Rev A. 1978;18(4):1652–1680.
- Yakushevich LV, Krasnobaeva LA. Vliyanie dissipacii i vneshnego polya na dinamiku lokalnih konformacionnih vozmuschenii v DNK. Biophysics. 2007;52(2):237–243.
- Yakushevich LV, Kashapova GR, Zakiryanov FK. Vliyanie periodicheskogo polyas postoyannoi i medlenno menyayuscheisya chastotoi na dvijenie kinka v dnk. Biophysics. 2012;57(1):21–26.
- http://www.lifesci.dundee.ac.uk/groups/mike_stark/pTTQ18_DNA.txt
- Grinevich AA, Yakushevich LV. Kinks behavior near the boundaries separating homogeneous regions of DNA. Mathematical Biology and Bioinformatics. 2015:10(1):164–177.
- Yakushevich LV, Krasnobaeva LA, Shapovalov AV. et al. Odno_i dvuhsolitonnie resheniya uravneniya sinus_Gordon v prilojenii v DNK Biophysics. 2005;50(3):450–455.
- Yakushevich LV, Krasnobaeva LA. Osobennosti dinamiki kinka v neodnorodnoi DNK. Biophysics. 2008;53(1):36–41.
- Bishop AI, Nieminen TA, Heckenberg NR, et al. Optical application and measurement of torque on micropartic les of isotropic nonabsorbing material. Phys Rev A. 2003;68(3):033802.
- La Porta A, Wang MD. Optical torque wrench: angular trapping, rotation, and torque detection of quartz microparticles. Phys Rev Lett. 2004;92(19):190801.
- Klaue D, Seidel R. Torsional stiffness of single super‒paramagnetic microspheres in an external magnetic field. Phys Rev Lett. 2009;102 (2):028302.
- Harada Y, Ohara O, Takatsuki A, et al. Direct observation of DNA rotation during transcription by Escherichia coli RNA polymerase. Nature. 2001;409(6816):113–115.
- Lipfert J, Kerssemakers JWJ, Jager T, et al. Magnetic torque tweezers: measuring torsional stiffness in DNA and RecA-DNA filaments. Nat Methods. 2010;7(12):977–980.

© . This is an open access article distributed under the terms of the,
which
permits unrestricted use, distribution, and build upon your work non-commercially.







