Abstract
The enzyme-linked immunospot assay (ELISpot) is one of the most frequently and widely used methods to detect multiple secretory products from a single cell. There are two main approaches to defining positivity criterion for the quantitative ELISpot assay data: ad hoc (Empirical) rules and hypothesis test methods such as t-test and DFR. Hypothesis tests are indeed important to detect whether the test samples are significantly different from the controls. However, the consistency of the results is also important for clinical tests. This research proposed a new method (called the LOD method) focusing on the reproducibility of the results. Simulation and real data analysis showed that T-test and DFR(eq) have higher test power but LOD method has the highest level of reproducibility.
Keywords: ELISpot, hypothesis test, statistics, positivity
Introducton
The enzyme-linked immunospot assay (ELISpot), which was first described in 1983, is one of the most frequently and widely used functional assays for single-cell analysis.1–5 The principles of ELISpot are based on the ELISA technique, with the difference that in ELISpotanalytes secreted by cells plated into 96-well plates are immediately captured by an antibody used to coat the membrane bottom of such plates. After the removal of cells, the captured analyte, either a cytokine, chemokine, immunoglobulin (Ig) or other secreted molecule, is made visible by a biotin-avidin-enzyme-substrate development cascade, which results in colored spots (the color depends on the enzyme and substrate chosen for the assay) on a whitish membrane. The colored spots are usually enumerated using an automated ELISpot reader system. Each spot represents one cell that secreted the analyte of interest, and it represents the integration of the amount of analyte secreted during the assay duration, as well as its secretion kinetics.
Thus, ELISpot assay allows the visualization and enumeration of multiple secretory products from single cells. One common application is the count of CD4+ and CD8+ T cells that secrete cytokines in response to an antigenic stimulus at the single cell level. Multiple peptide pools are typically used for stimulation. The raw form of the data arising from the ELISpot assay is the number of spot forming cells (SFCs) for each experimental and control (negative and positive) well, each of which are often performed in replicates (It is a common practice that 6 replicates are run for the negative controls, 3 replicates are run for the test samples). A test sample is subsequently categorized as positive or negative depending on whether or not the number of SFCs in the experimental wells is significantly greater than in the control wells. The word ‘significantly’ is loaded with a variety of implications, it is the goal of this research to delineate and distinguish the difference in statistical, biological, and analytical aspects.
There are two main approaches to defining a positivity criterion for the quantitative ELISpot assay data: ad hoc (Empirical) rules and hypothesis test. The empirical approach uses a threshold and/or a fold difference between the experimental and negative control wells that is determined based on empirical reasons, which is meant to represent “biological significance” according to the researcher’s opinion. For example,6 declares a positive response for antigens where the average number of SFCs in the peptide pool wells is greater than or equal to 11 SFCs/well and is also at least four times the average of the negative control wells (where each well contains 200,000 cells).
A statistical hypothesis test uses the non-zero difference (in statistical sense) between the experimental and negative control wells as the criteria for determining positivity. This approach is designed to control the false positive rate and has the ability to detect weak but truly non-zero responses (power). Surveying the literature, the considered statistical methods for ELISpot assays include t-test, Wilcoxon rank sum test, score test based on binomial distributions, Severini test that considers the over-dispersion, and the bootstrap methods that has gained some popularity in recent years. This research primarily considers t-test and the distribution-free re-sampling method (DFR) which is a permutation-based method.7
The DFR method, as the name indicates, a distribution-free method, was proposed to address concerns with t-test which requires certain assumptions about the data (e.g. normality, variance homogeneity). The DFR method employs a permutation test whereby only the independent replicates of a single peptide pool and the negative controls from an individual are permuted. The test statistic employed is simply the difference in the sample means of the peptide pool and negative control replicates.
Scaling the difference by the variance is not applied for DFR method since it is deemed “undesirable as it gives large test statistics when the variance is small, even when the difference is small also. Such cases should not provide evidence to support a positive call. Also, the variance estimates can be unreliable with a small number of replicates. For these reasons, the test statistic does not involve the variance”. However, a variance filter for extreme outliers is imposed at the lab for quality control. Specifically, an assay is deemed as an outlier if
Where the ‘Variance’ is the intra-replicate variation was calculated as the sample variance of the replicates; the number one is added to the median to avoid division by a zero median. That is, if the peptide pool for which the ratio of the variance to the median+1 exceeds 100%, that assay is re-run. For a Poisson distribution, the ratio of variance/mean (called dispersion index) follows a χ2 distribution with degree of freedom n-1 (where n is the number of replicates).
Both empirical methods and hypothesis test methods have pros and cons. The empirical method is easy to implement, it incorporates the researcher’s subjective “requirement” (subjective may not be a bad thing). Ad hoc approach is not uncommon, for example, FDA guideline suggests that “LLoQ needs to be at least 4 times bigger than LoB”. Here the number 4 is based on empirical reasons. The main drawback of the ad hoc method is that it doesn’t control false positive or false negative rates. In general, hypothesis test methods, on the other hand, are purely data-driven and objective (objectivity can also be both bad and good). They may detect a statistically significant difference that is of no sufficient biological meaning. Therefore, there are some ‘hybrid’ methods used. For instance, DFR (2X) tests whether the mean of the test group is more than two times the mean of the control group. Here 2X is clearly an empirical decision. A brief summary of the methods is provided in table 1 below.
Method |
Pros |
Cons |
Empirical Rules |
Intuitive, ‘significance’ is not driven solely be statistical testing, but rather driven by biological expectations/opinions |
Doesn’t control false positive/negative rates, doesn’t consider variation of the means. Can be adapted to establish CI using Feller’s theorem. |
Hypothesis test |
T-test |
Easy to implement |
Assumes normality and quite often variance homogeneity. Sample size plays a very important role in the resulting pvalue |
DFR (eq) |
Permutation-based method, ‘distribution-free’. |
Sample size requirement, used an ‘empirical’ rule on variance as a QC criteria (<100%), no division by SD
Not consider the consistency of the ‘positive’ call, pure hypothesis test on mean difference |
DFR (2x) |
Similar to the Empirical approach, requires 2-fold difference |
Where does the ‘2’ come from? A number of convenience. Obviously a hybrid of an ST and empirical rule. |
Table 1 Summary of the pros and cons for the current methods
Empirical or statistical, parametric or non-parametric, the goal is to control the false positive and false negative error rates. The fundamental question is then what is considered an ‘error’. For empirical rules, it is an error of false positive when a test is claimed to be positive if the difference in mean values is less than 2 fold; for hypothesis test method, an ‘error’ is purely determined by whether the null hypothesis
is true, regardless of how small the difference might be. Hence, a type I error is committed if a sample is called positive but in truth
, whereas a type II error is committed if the sample is not called positive when in truth
.
Why 2-fold, 100% CV, or 2X? There are no theoretical bases for the choice of the criteria, they are numbers chosen mostly because of convenience. Instead, any number we choose should help us achieve certain goal – false positive control, false negative control, QC failure rate, clinical and economical impacts, etc. These numbers should be chosen based on the property of the data distribution, which is dependent upon the data generation mechanism. Therefore, it is critical to understand the underlying mechanism of data generation. Such a mechanism determines the model for us, rather than we determine the model for the data.
In this research, T-test is considered here because it is still commonly applied due to its ease of use. Empirical method is not considered due to its obvious lack of controls over false positive and false negative errors. The focus of this paper is to compare DFR method and the proposed method, LOD method, which emphasizes the reproducibility of the decision call rather than the statistical significance.
Material and methods
Statistical description of ELISpot data
Suppose that we have n replicate wells for cells stimulated with a particular peptide pool and m replicate wells containing cells serving as a negative control, all at the concentration (often 200,000 cells/well). Let
be the number of SFCs per well for the m control wells, and
be the number of SFCs per well for the n test wells treated with the peptide pool. Let
be the per-well average for a particular peptide pool and let
be the corresponding average for the control wells. Assume the distribution governing the number of SFCs/control well follows a distribution with true (but unknown) SFC of
, denoted by
assume the distribution governing the number of SFCs/test well follows a distribution with true (but unknown) SFC of
, denoted by
. The typical goal is to evaluate if
based on the observed data. Note that the two distributions,
and
are of the same family (e.g. both are Poisson) but with different parameters (e.g. mean and/or variance can be different).
Since the assay result for each well is the count of ‘event’, Poisson and Binomial distributions are typically used to characterize this variable. While both measure the number of certain random events (or "successes") within a certain frame, binomial distribution describe the process as “given a (fixed) number, N, of "attempts" (cells), each of which has the same probability of success, p”; Poisson distribution, on the other hand, describe the process as “with the same probability success, p, the number of successes observed from a random number of attempts”. In theory, given a Binomial distribution with probability of success p, if p is a small value such that when
, Np → λ, then this distribution approaches a Poisson distribution with parameter λ. In practice, the difference is very small in whether or not N is considered fixed.
Another way to see the connection between the two distributions is as follows. Consider the general case of enumerating a total of N events, of which K meet a certain criterion (positives). The proportion of positives, p=K/N (0 ≤ p ≤ 1), is the estimate of the probability of the particular event being observed. For a binomial distribution, the variance (Var) of the random variable K is estimated as:
When the event is rare, p is very small, and so 1-p is very close to 1. The variance is approximately
The variance equals the mean, which is the case for a Poisson variable. In other words, when p is small, Poisson distribution is an approximation of a binomial distribution, and thus both distributions are reasonable for ELISpot assays.
Let N denote the total number of collected target cells in the sample pool from which replicates are drawn, and let K0 denote its true (but unknown) positive cells within the N cells. In other words, the proportion (‘event rate’) is λ=K0/N. When replicates (working samples)
are drawn from this sample pool, the number of positives cells for a replicate i with a total of target cells is highly unlikely to be exactly equal to
(the theoretically expected number). Due to random chance, some replicates will have more positive cells than the theoretical expectation, some will have less. This variation can be modeled as
Where
the expected number of positive cells is,
is the deviation of replicate
from the theoretical expectation. As discussed earlier,
can be generally assumed to follow a Binomial or a Poisson distribution. This variation can be termed as ‘sampling’ variability.
For each working sample, due to the assay variability, the readout of the assay is also highly unlikely to be exactly the same as the truth
. The observed number of positives can be modeled as
Where
represents the assay noise, which can depend upon factors such as operators, reagents, plate effects, instrument variabilities, signal computer processing and data analysis, and so on. This variation can be termed as ‘assay’ or ‘analytical’ variability.
In a typical ELISpot experiment, the data is composed of the control group and the test group. The data of the control group can be modeled as
And the data of the test group can be modeled as
The goal of the analysis is to assess if
and
are significantly different.
LOB-LOD-LOQ paradigm
Statistical test is indeed important in evaluating whether the test samples are significantly different from the controls. In clinical assays, it is also (maybe more) important that the results are consistent. For example, if a sample is determined to be HIV-positive, we’d hope this result is reproducible so we have high confidence in the decision. That is, the decision that a sample is HIV-positive needs to be consistent(e.g. 95% concordant) if the assay is repeated multiple times. The chart below describes the fundamental difference between the three approaches.
The test result based on the LOD method is not impacted by the sample size n, it only depends on how much the two distribution overlap. Conversely, the hypothesis test methods may miss a big difference due to a small sample size, or pick up a small difference due to a large sample size.
The desire for controlling the amount of distribution overlap (instead of just the p value of a hypothesis test) fits into the frame work of LOB-LOD-LOQ. The concept of LOB, LOD, and LOQ are illustrated by the figure below. Simply put, LOB is the limit of ‘blanks’, the upper 95th percentile (typically) of the controls. LOD is the number of events such that if the sample is repeatedly measured by incorporating different variation factors, its 5th percentile (typically) is equal to LOB. LOQ is the quantification limit that incorporates the desired assay goals (typically assay bias and precision). For example, LOQ is the number of event such that the CV of the repeated measurements is no greater than 20%. For more details on the definition and calculation of LOB, LOD, LOQ, please read CLSI guideline EP17.8
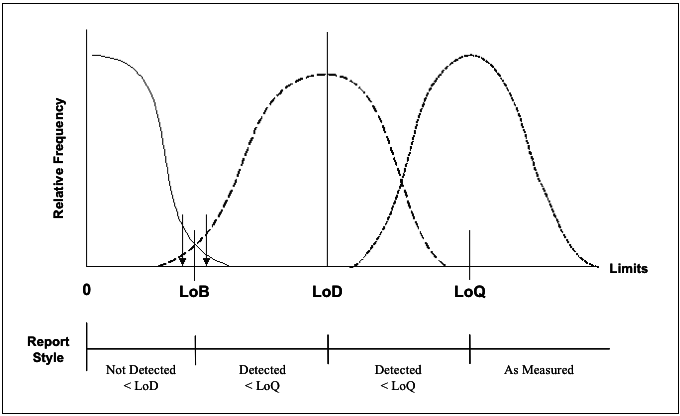
Figure 1 Schematic illustration of the Limits of detection.
Given the fact that there are only very limited number of replicates for each condition, and the best estimates of
and
are simply the observed mean values. With these estimates, the LOD method requests that the overlaps of the two distributions are no more than 5%.
Analysis procedure
When two Poisson variables X and Y are independent, with event rate
and
respectively, the difference of the two variables Z=Y-X follows a Skellam distribution with probability mass function (discrete variable) given by
Where
is the modified Bessel function of the first kind,
and
are the event rates for the two Poisson distributions.9
For the n replicates of the test samples,
, each of with follows a Poisson distribution with mean
, the sum
follows a Poisson distribution with mean and variance equal to
, the sum of the m replicates of the controls
follows a Poisson distribution with mean and variance equal to
. The difference
follows a Skellam distribution with parameter
- its mean is
and variance is
. The maximum likelihood estimate (MLE) for
is
; similarly, the MLE for
is
.
The 95th percentile of the Skellam distribution under the NULL (the test sample has the same positivity rate) is
. Where is the critical value that corresponds to the 95%-tile of the distribution, here we choose
, a value that is coincidentally the same as the 95% - tile critical value of a standard normal distribution (see Supplementary materials for the analysis for supporting this decision). Note that the LOB increases with the event counts.
LOD is an event rate of X such that 95% of the distribution of difference (Poisson variable with mean X-
, variance X+
) is above LOB. Putting this into a mathematical equation, it is
Here is the type II error rate. Setting
and solvingthe equation for X, we get
Where
.
The figure below gives a schematic view of the Skellam distribution. In this example, the mean of the Control is
, the mean of the test sample ranges from
. When
, the Test and the Control have no difference, the difference follows a Skellam distribution with mean 0 and variance
(the black solid line), thus the LOB is simply the upper 95%-tile of this distribution. When
, the Skellam distribution has 95% of the distribution above the LOB, thus the LOD is
.
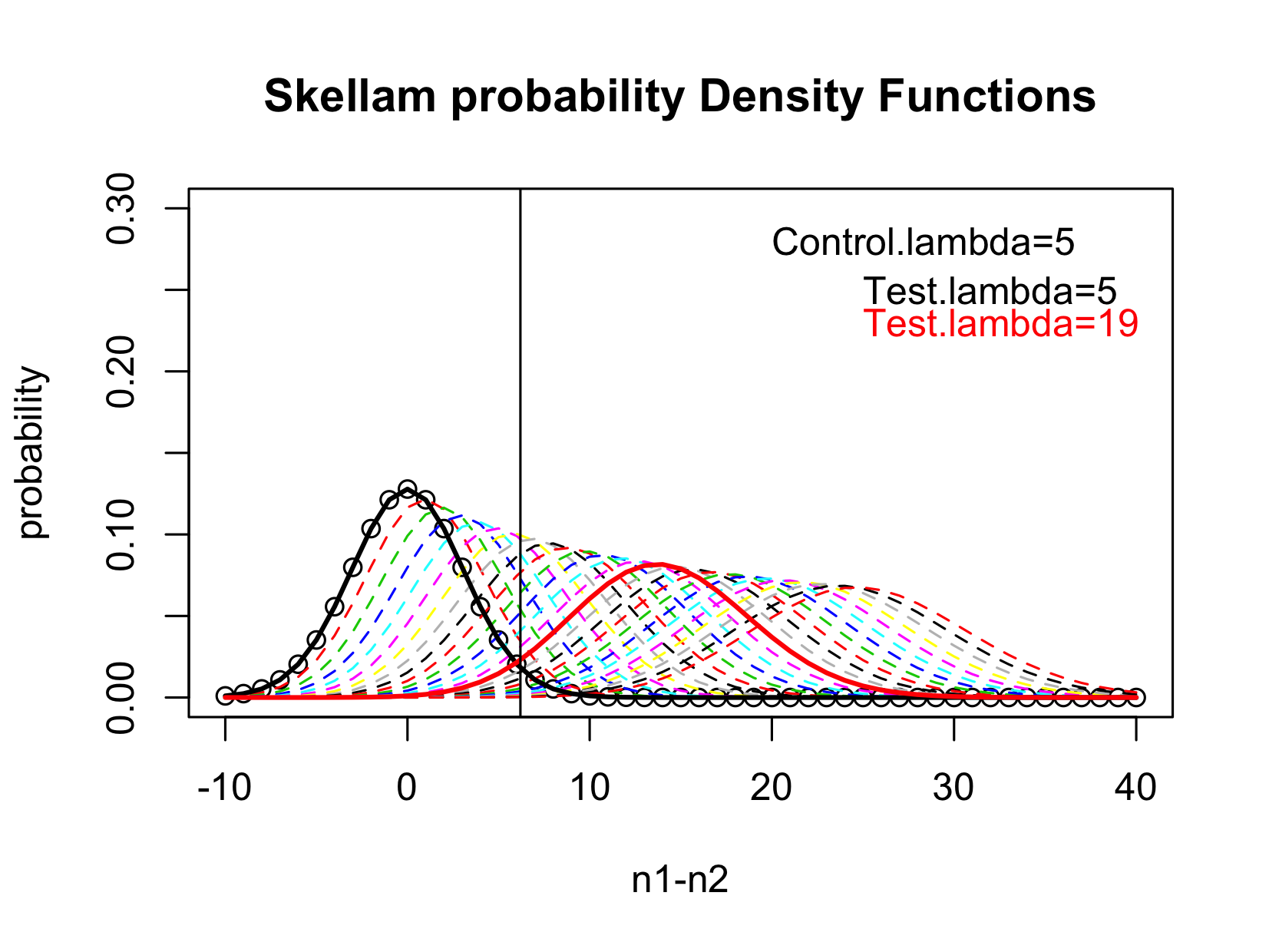
Figure 2 Illustration of the Identification of LOD.
Operation procedure
- Calculate the mean and the sum of the controls. The mean gives the estimate of
; the sum gives the estimate of the mean of the Poisson distribution
.
- The LOB is estimated as
, where
- LOD is the
such that
Where
.
- If the observed sum of the Test samples is more than the calculated LOD, then the Test sample is claimed to be Positive; otherwise it is negative.
Results and discussion
Simulation
Simulations were conducted to compare the performance of the four methods. For each simulated ‘experiment’, the data consisted of 6 replicates from the Control condition and 3 replicates from the Test condition. It was assumed that the data from both conditions followed Poisson distributions. Two event-rate scenarios were considered for the Controls:
and
(i.e. the event rate for the Test ranges from 30 to 60). For the Test condition, the difference in event rate ranged from 0% to 100% for the case of
, and from 0% to 200% for the case of
( i.e, the event rates range from 10 to 20). The cases of 0% change provide assessment of the false positive rate; the other cases provide the assessment of the test power.
For each case 1,000 simulation runs were conduction. Figure 3 below show the simulation result. The most powerful test in these four methods is DFR (eq), followed by t-test and then the LOD method. As expected the DFR (2x) shows the least power. For the case of Control=10, the LOD method doesn’t show any power until the difference is over 50%, in which case the number of events in the test sample is 15. Since for a Poisson distribution with event rate of 10, its standard deviation is 5, the LOD method essentially treats any change that is below one standard deviation as irreproducible and thus determined as insignificant. For the case of Control=30, the power starts when the difference is about 30% (so the number of events is about 40).
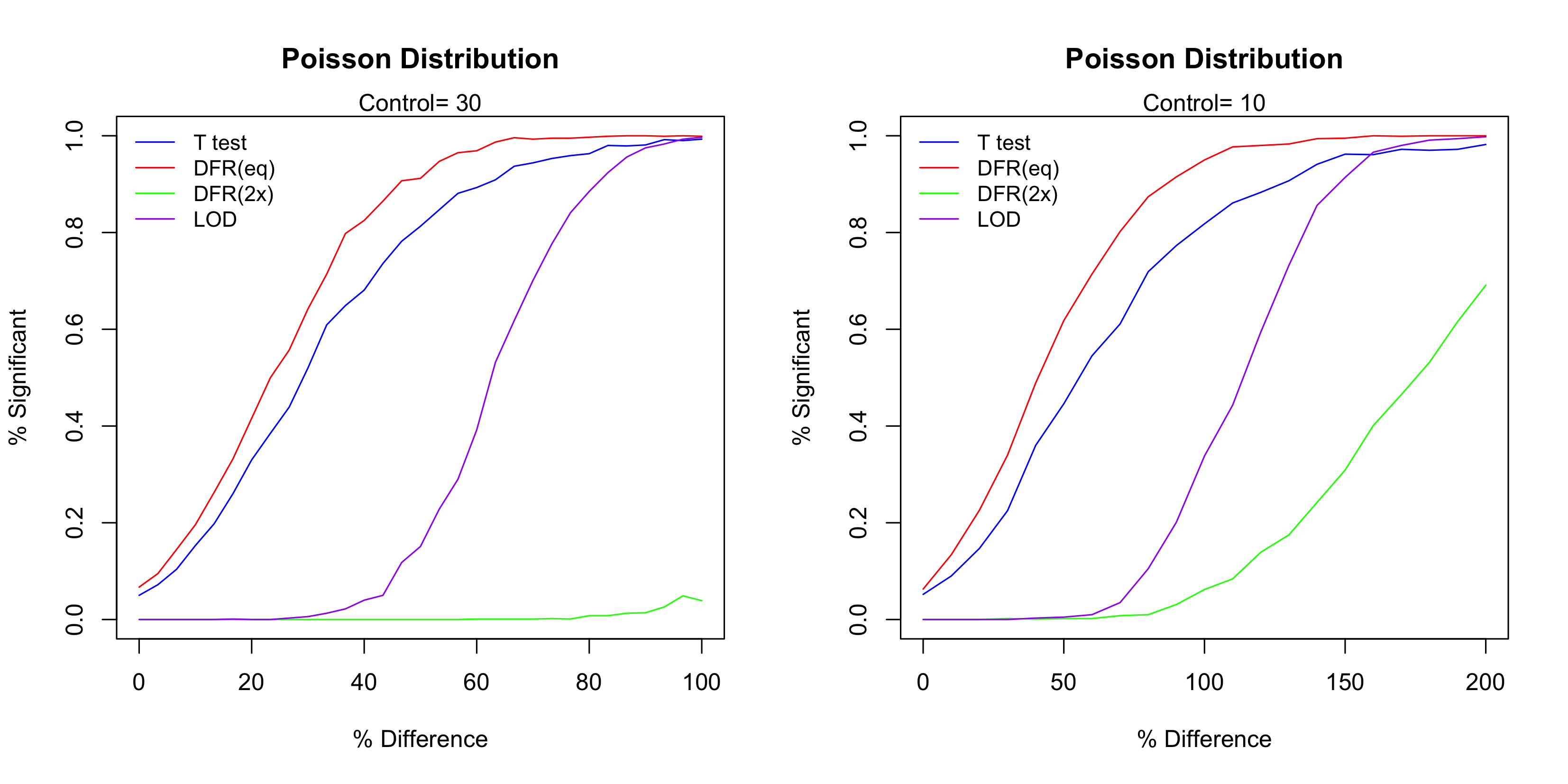
Figure 3 The performance of the four test methods.
It is true that T-test and DFR (eq) have higher test power than the LOD method, but notice that the LOD method has the steepest curve. This indicates that LOD method has the highest level of reproducibility, which means the highest consistency of the significant calls. To see this, let’s use Control=10 as the example and consider when the Difference is about 50%. In this case, out of the 1,000 simulation runs DFR (eq) called about 40% time significant and 60% negative, so the reproducibility is 40%. On the other hand, almost none of them were called significant. Though the truth is indeed that the Test is different from the Control, but the LOD method requires a higher level of reproducibility (thus higher level of confidence) to determine a positive case. The steep curve of the LOD method means that the ‘gray zone’ (the uncertainty range) is narrow, which is a good characteristic of diagnostic tests and assay procedures.10
Application to real data
Data from the three the European CIMT Immuno-guiding Program (CIP) proficiency panel phases were used to compare different analysis methods.11–13 In the referred studies, groups of 11, 13 and 16 laboratories (phases I, II and III, respectively) quantified the number of CD8 T cells specific for two model antigens within PBMC samples that were centrally prepared and then distributed to the participating laboratories. All participants were allowed to use their preferred ELISPOT protocol. Therefore, the data sets generated in these studies can be considered representative of results generated by a wide range of different protocols commonly applied within Europe. Each participating center was asked to test in triplicate 18 preselected donors (5 in the first phase, 8 in the second phase and 5 in the third phase) with two synthetic peptides (HLA-A*0201 restricted epitopes of CMV and Influenza) as well as PBMCs in medium alone for background determination. In total, nineteen different laboratories participated in at least one of the three phases and they reported a total of 717 triplicate experiments (this includes control and experimental wells).
In the CIP study, the donors were selected so that 21 donor/antigen combinations (6 in the first phase, 8 in the second phase and 7 in the third phase) were expected to demonstrate a positive response with the remaining 15 donor/antigen combinations not expected to demonstrate a positive response. In this research, we specifically selected those cases that are positive in only one of the scenario (CMV or FLU, not both) so that the data from the 2 triplicates of the negative conditions are pooled, so that for each test the comparison is between the triplicate of the positive condition versus the 6 replicates from the negative condition. Similarly, for the negative cases, we only considered those that negative in both CMV and FLU so that we can compare either CMV or FLU to the rest, which also has n=3 versus n=6.
The table below shows the donors that were used in this research. Note that for the Negative cases, each donor can be used for testing both CMV positivity and FLU positivity, so from the analysis point of view we have 4 instead of 2 true negative cases.
|
CMV Positive |
FLU Positive |
Negative |
Phase I |
|
Donor 2 and 3 |
Donor 4 |
Phase II |
Donor 8 |
Donor 1, 5, 6, and 7 |
Donor 3 |
Phase III |
Donor 1 |
Donor 4 and 5 |
|
Table 2 The known Positive and Negative cases in CIP Study
Figure 4 plots the variability versus the mean for the triplicate experiments. The black line represents the 45-degree line (X=Y), the red line is the spline fit. We can see that the relationship of variance = mean can be entertained, therefore a Poisson model is reasonable.
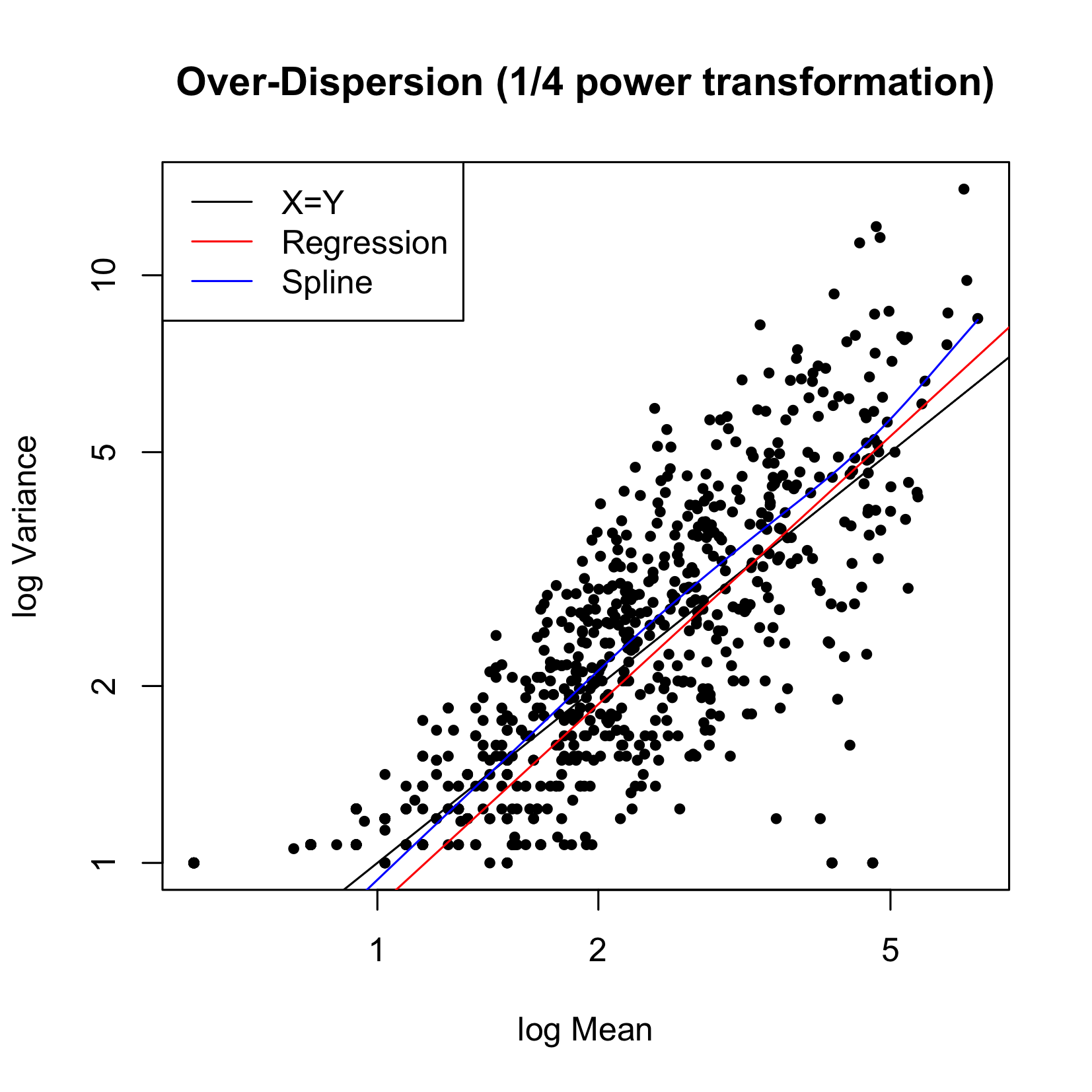
Figure 4 Variance versus Mean for CIP data.
Since different labs used different protocols, the number of targeted cells is “standardized” to be 500,000 so that the number of total cells is comparable across assays. This means that is a lab had 250,000 as the number of targeted cells and found 4 events, the standardized number of event is 8. Note that, this standardization is unnecessary if the percent-positivity is used, but is useful if the count of positive cells is used to quantify the response. Accuracy, sensitivity, specificity, positive predicted value (PPV), and negative predicted value(NPV) are calculated to compare the four test methods. (Table 3) is the contingency table of predicted and true values. In table 3, b is the type I error, which is the number of false positive samples. C is the type II error, which equals to the number of false negative samples. Accuracy
is the sum of true positive and true negative divided by the number of total samples. Sensitivity is
and specificity is
. Sensitivity would decrease if type II error rate increases. Similarly, specificity would decrease if type I error rate becomes larger. PPV
means how many samples is true positive in the samples predicted to be positive while NPV
is the rate of true negative in the samples predicted to be negative.
|
Truth |
|
Positive |
Negative |
Total |
Test results |
Positive |
a |
b |
a+b |
Negative |
c |
d |
c+d |
|
Total |
a+c |
b+d |
a+b+c+d |
Table 3 Contingency table of predicted and true values
Table 4 below shows the performance summary statistics of each test method. Overall, DFR has the best performance, T-test and LOD have similar performance, and the worst in the four tests is DFR2x. This result reasonably agrees with the simulation study.
|
T-test |
DFR |
DFR2x |
LOD |
Accuracy |
0.791 |
0.821 |
0.694 |
0.786 |
Sensitivity |
0.723 |
0.764 |
0.595 |
0.730 |
Specificity |
1.000 |
1.000 |
1.000 |
0.958 |
PPV |
1.000 |
1.000 |
1.000 |
0.982 |
NPV |
0.539 |
0.578 |
0.444 |
0.535 |
Table 4 Performance of the Four Methods on CIP Data
Discussion
The simulations and applications used Poisson distribution simply as an example. The idea can be easily generalized to distributions of any known or unknown formats. The critical factors are simply the mean and the standard deviation of the distribution that are used to determine the LOB and LOD.
Conceptually, the LOD method is very closely related to Cohen’s D, which is defined as
, where
is the difference of the sample means, and s is the pooled standard deviation. Notice that the typical test statistics is
. Notice that the difference is in the contribution of the sample size. The typical statistical test can achieve a small p value by having a large enough sample size (lots of replicates), but the results of each of the individual replicate can be higher irreproducible. On the contrary, the LOD method guarantees that the overlap of the two distributions, the sample size doesn’t have impact on the decision making (though in reality a larger sample size gives a better estimation of the distribution).
Figure 5 below show the histogram of 2 pooled distributions that have Cohen’s D of 1-4. Though in truth the two distributions are different for d=1, we can see that they are not separable. It is easy to imagine how low our confidence would be if the test determines that Test is different Control.

Figure 5 Illustration of Cohen’s D.
Conclusion
This research proposed and investigated a statistical method for determining the positivity of the immune-response using ELISpot assays. Different from the typical statistical methods that focus on the pvalue of a hypothesis test, this new method focuses on the reproducibility of the decision. This is critical in the use of clinical biomarkers that are used for diagnostic, prognostic, and predictive purposes. In these applications, the typical hypothesis mainly concerns with the statistical evidence that is based on the current given data, the LOD method mainly concerns with the analytical variability and focuses the reproducibility of the future data.
Acknowledgement
We would like to thank the European CIMT Immuno-guiding Program (CIP) proficiency panel for sharing the real data set.
Supplementary materials
Decision for choosing z alpha =1.645:
The critical value of 1.645 is determined by empirical observations, it is an approximation to the critical factor for Skellam distributions. The two plots below gives 2 examples. The first is when the Control sample # of events = 1, the Test sample # of events varies from 1 to 50; the 2nd plot is when the Control # of events = 10 whereas the Test sample # of events varies from 10 to 50. The ‘z factor’ on the Y-axis is (mean – 5th percentile)/std.
Where ‘mean’ is the mean of each Skellam distribution, ‘5th percentile’ is the 5%-tile of the Skellam distribution, and ‘std’ is the standard deviation of the Skellam distribution. It can be seen that 1.645 is a good approximation to all of the z factor values, this is called “
” from now on.


Note that the 95% upper limit (UL),
, depends on the event rate of the control sample. Here if we assume that the target total # of cells is 10,000 and 100,000 is used to normalize the count of interesting events. In the following 3 pairs of plot, 3 different situations are assumed:
(which closely mimics the IFNg+ event rate in the pre-clinical model),
, and
. Again, note that the upper 95% limit for each of these individual Poisson distribution is roughly
Therefore the 95% upper limit for the 3 scenarios are about 3, 5, and 9 respectively, these are the ‘maximum’ # of events possibly observed in the controls. This information will help us determine likely (expected) event rate for the controls (
), which can be dependent upon the assay and parameter of interest. The methodology developed here is for general purposes.
Using the first pair as an example, and assuming
, plotted are a series of ‘probability density plots’ for different
values, ranging from 1 to 30. The black solid curve is the NULL distribution when
. The vertical black line is the LOB = 0+1.645
=2.33. The red solid curve is corresponds to the test sample (
in this case) such that 95% of the Y-X values are above LOB. Therefore, the LOD in terms of the difference is
; in terms of the event rate for the test sample
. The right panel plots the %’s of the curve for each case so that is above the LOB. The blue dashed line corresponds to 95%, the black dashed line corresponds to 5%. The red dashed line identifies the value of
so that 95% of its curve is above LOB.


Conflicts of interest
References
- Czerkinsky CC, Nilsson LA, Nygren H, A solid-phase enzyme-linked immunospot (ELISPOT) assay for enumeration of specific antibody-secreting cells.J Immunol Methods. 1983;65(1-2):109–121.
- Navarrete MA. ELI spot and DC-ELI spot assay to measure frequency of antigen-specific ifnγ-secreting cells. Methods Mol Biol. 2015;1318:79–86.
- Shrestha R, Gyawali P, Yadav BK, et.al. In-vitro assessment of cell-mediated immunity by demonstrating effector-t cells for diagnosis of tuberculosis in Nepalese subjects." Nepal Med Coll J. 2015;13(4):275–278.
- Jin C, Roen DR, Lehmann PV, et al. An Enhanced ELISPOT Assay for sensitive detection of antigen-specific t cell responses to borrelia burgdorferi. Cells. 2013;2(3):607–620.
- Cox JH, Ferrari G, Janetzki S. Measurement of cytokine release at the single cell level using the ELISPOT assay. Methods. 2006; 38(4):274–282.
- Mogg R, Fan F, Li X, et al. Statistical cross-validation of Merck's IFN-γ ELISpot assay positivity criterion. AIDS Vaccine, New York, NY; 2003.
- Hudgens MG, Self SG, Chiu YL, et al. Statistical considerations for the design and analysis of the ELISpot assay in HIV-1 vaccine trials. J Immunol Methods. 2004;288(1-2):19–34.
- CLSI. Evaluation of Detection capability for clinical laboratory measurement procedures; approved guideline. 2nd ed. CLSI document EP17-A2. Wayne, PA: Clinical and Laboratory Standards Institute. 2012.
- Alzaid, Abdulhamid A, Maha A. On The poisson difference distribution inference and applications. BULLETIN of the Malaysian Mathematical Sciences Society. 2010;33(1):17–45.
- CLSI. User protocol for evaluation of qualitative test performance; Approved guideline, 2nd ed. CLSI document EP12-A2. Wayne, Clinical and Laboratory Standards Institute. 2008.
- Britten CM, Gouttefangeas C, Welters MJ, et al. The CIMT-monitoring panel: A two-step approach to harmonize the enumeration of antigen-specific CD8+ T lymphocytes by structural and functional assays. Cancer Immunol Immunother. 2007;57(3):289–302.
- Mander A, Gouttefangeas C, Ottensmeier C, et al. Serum is not required for ex vivo IFN-γ ELISPOT: A collaborative study of different protocols from the European CIMT Immunoguiding program. Cancer Immunol Immunother. 2010;59(4):619–627.
- Moodie Z, Huang Y, Gu L, et al. Statistical positivity criteria for the analysis of ELISpot assay data in HIV-1 vaccine trials. J Immunol Methods. 2006;315(1-2):121–132.

© . This is an open access article distributed under the terms of the,
which
permits unrestricted use, distribution, and build upon your work non-commercially.






