eISSN: 2378-315X

Biometrics & Biostatistics International Journal

Correspondence:

Received: January 01, 1970 | Published: ,

Citation: DOI:

Download PDF

Abstract

In this paper a continuous distribution named “Garima distribution” has been suggested for modeling data from behavioral science. The important properties including its shape, moments, skewness, kurtosis, hazard rate function, mean residual life function, stochastic ordering, mean deviations, order statistics, Bonferroni and Lorenz curves, entropy measure, stress-strength reliability have been discussed. The condition under which Garima distribution is over-dispersed, equi-dispersed, and under-dispersed are presented along with other one parameter continuous distributions. The estimation of its parameter has been discussed using maximum likelihood estimation and method of moments. The application of the proposed distribution has been explained using a numerical example from behavioral science and the fit has been compared with other one parameter continuous distributions.

Keywords: lifetime distribution, moments, hazard rate function, mean residual life function, mean deviations, order statistics, estimation of parameter, goodness of fit

Introduction

The modeling and analyzing lifetime data are crucial in many applied sciences including behavioral science, medicine, engineering, insurance and finance, amongst others. There are a number of continuous distributions for modeling lifetime data such as exponential, Lindley, gamma, lognormal, and Weibull and their generalizations. The exponential, Lindley and the Weibull distributions are more popular than the gamma and the lognormal distributions because the survival functions of the gamma and the lognormal distributions cannot be expressed in closed forms and both require numerical integration. Though each of exponential and Lindley distributions has one parameter, the Lindley distribution has one advantage over the exponential distribution that the exponential distribution has constant hazard rate whereas the Lindley distribution has monotonically decreasing hazard rate.

Recently Shanker^1–4 has introduced new lifetime distributions, namely Shanker, Akash, Aradhana, and Sujatha distributions for modeling lifetime data from biomedical sciences, engineering and behavioral sciences and showed its superiority over Lindley⁵ and exponential distributions. The probability density function (p.d.f.) and the cumulative distribution function (c.d.f.) of Sujatha, Aradhana, Akash, Shanker, Lindley and exponential distributions are presented in Table 1.

Distributions	Pdf	Cdf
Sujatha	$f_{6} (x; θ) = \frac{θ^{3}}{θ^{2} + θ + 2} (1 + x + x^{2}) e^{- θ x}$	$F_{6} (x, θ) = 1 - [1 + \frac{θ x (θ x + θ + 2)}{θ^{2} + θ + 2}] e^{- θ x}$
Aradhana	$f_{5} (x; θ) = \frac{θ^{3}}{θ^{2} + 2 θ + 2} {(1 + x)}^{2} e^{- θ x}$	$F_{5} (x; θ) = 1 - [1 + \frac{θ x (θ x + 2 θ + 2)}{θ^{2} + 2 θ + 2}] e^{- θ x}$
Akash	$f_{4} (x; θ) = \frac{θ^{3}}{θ^{2} + 2} (1 + x^{2}) e^{- θ x}$	$F_{4} (x; θ) = 1 - [1 + \frac{θ x (θ x + 2)}{θ^{2} + 2}] e^{- θ x}$
Shanker	$f_{3} (x; θ) = \frac{θ^{2}}{θ^{2} + 1} (θ + x) e^{- θ x}$	$F_{3} (x, θ) = 1 - \frac{(θ^{2} + 1) + θ x}{θ^{2} + 1} e^{- θ x}$
Lindley	$f_{2} (x; θ) = \frac{θ^{2}}{θ + 1} (1 + x) e^{- θ x}$	$F_{2} (x; θ) = 1 - [1 + \frac{θ x}{θ + 1}] e^{- θ x}$
Exponential	$f_{1} (x; θ) = θ e^{- θ x}$	$F_{1} (x; θ) = 1 - e^{- θ x}$

Table 1 pdf and cdf of Sujatha,⁴ Aradhana,³ Akash,² Shanker,¹ Lindley⁵ and exponential distributions

A new lifetime distribution

The probability density function (p.d.f.) of a new lifetime distribution can be introduced as

$f_{7} (x; θ) = \frac{θ}{θ + 2} (1 + θ + θ x) e^{- θ x}; x > 0, θ > 0$ (2.1)

We would call this distribution, “Garima distribution”. This distribution can be easily expressed as a mixture of exponential $(θ)$ and gamma $(2, θ)$ with mixing proportion $\frac{θ + 1}{θ + 2}$ . We have

$f_{7} (x, θ) = p g_{1} (x) + (1 - p) g_{2} (x)$ (2.2)

where $p = \frac{θ + 1}{θ + 2}, g_{1} (x) = θ e^{- θ x}, and g_{2} (x) = θ^{2} x e^{- θ x}$ .

The corresponding cumulative distribution function (c.d.f.) of (2.1) is given by

$F_{7} (x; θ) = 1 - [1 + \frac{θ x}{θ + 2}] e^{- θ x}$ ; $x > 0, θ > 0$ (2.3)

The graphs of the p.d.f. and the c.d.f. of Garima distributions for different values of $θ$ are shown in Figure 1.

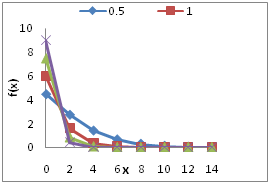
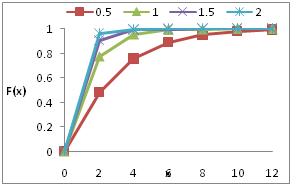
Figure 1 Graphs of the pdf and cdf of Garima distribution for various values of the parameter θ.

Moments and related measures

The $r$ the moment about origin of Garima distributon (2.1) has been obtained as

$μ_{r}^{'} = \frac{r! (θ + r + 2)}{θ^{r} (θ + 2)}; r = 1, 2, 3, ...$

and so the first four moments about origin as

$μ_{1}^{'} = \frac{θ + 3}{θ (θ + 2)}$ , $μ_{2}^{'} = \frac{2 (θ + 4)}{θ^{2} (θ + 2)}$ , $μ_{3}^{'} = \frac{6 (θ + 5)}{θ^{3} (θ + 2)}$ , $μ_{4}^{'} = \frac{24 (θ + 6)}{θ^{4} (θ + 2)}$

Using the relationship between central moments and the moments about origin, the central moments of Garima distribution are obtained as

$μ_{2} = \frac{θ^{2} + 6 θ + 7}{θ^{2} {(θ + 2)}^{2}}$

$μ_{3} = \frac{2 (θ^{3} + 9 θ^{2} + 21 θ + 15)}{θ^{3} {(θ + 2)}^{3}}$

$μ_{4} = \frac{3 (3 θ^{4} + 36 θ^{3} + 134 θ^{2} + 204 θ + 111)}{θ^{4} {(θ + 2)}^{4}}$

Thus the coefficient of variation $(C . V)$ , coefficient of skewness $(\sqrt{β_{1}})$ , coefficient of kurtosis $(β_{2})$ and index of dispersion $(γ)$ of Garima distribution are obtained as

$C . V = \frac{σ}{μ_{1}^{'}} = \frac{\sqrt{θ^{2} + 6 θ + 7}}{θ + 3}$

$\sqrt{β_{1}} = \frac{μ_{3}}{μ_{2}^{3 / 2}} = \frac{2 (θ^{3} + 9 θ^{2} + 21 θ + 15)}{{(θ^{2} + 6 θ + 7)}^{3 / 2}}$

$β_{2} = \frac{μ_{4}}{μ_{2}^{2}} = \frac{3 (3 θ^{4} + 36 θ^{3} + 134 θ^{2} + 204 θ + 111)}{{(θ^{2} + 6 θ + 7)}^{2}}$

$γ = \frac{σ^{2}}{μ_{1}^{'}} = \frac{θ^{2} + 6 θ + 7}{θ (θ + 2) (θ + 3)}$

The condition under which Garima distribution is over-dispersed $(μ < σ^{2})$ , equi-dispersed $(μ = σ^{2})$ and under-dispersed $(μ > σ^{2})$ are presented in Table 2 along with other lifetime distributions.

Lifetime Distributions	Over-Dispersion $(μ < σ^{2})$	Equi-Dispersion $(μ = σ^{2})$	Under-Dispersion $(μ > σ^{2})$
Garima	$θ < 1.164247938$	$θ = 1.164247938$	$θ > 1.164247938$
Sujatha	$θ < 1.364271174$	$θ = 1.364271174$	$θ > 1.364271174$
Aradhana	$θ < 1.283826505$	$θ = 1.283826505$	$θ > 1.283826505$
Akash	$θ < 1.515400063$	$θ = 1.515400063$	$θ > 1.515400063$
Shanker	$θ < 1.171535555$	$θ = 1.171535555$	$θ > 1.171535555$
Lindley	$θ < 1.170086487$	$θ = 1.170086487$	$θ > 1.170086487$
Exponential	$θ < 1$	$θ = 1$	$θ > 1$

Table 2 Over-dispersion, equi-dispersion and under-dispersion of Garima, Sujatha,⁴ Aradhana,³ Akash,² Shanker,¹ Lindley,⁵ and exponential distributions for varying values of their parameter θ

Generating functions

The moment generating function $(M_{X} (t))$ , characteristic function $(φ_{X} (t))$ , and cumulant generating function $(K_{X} (t))$ of Garima distribution (1.3) are given by

$M_{X} (t) = (1 - \frac{(θ + 1) t}{θ^{2} + 2 θ}) {(1 - \frac{t}{θ})}^{- 2}, | \frac{t}{θ} | \leq 1$

$φ_{X} (t) = (1 - \frac{(θ + 1) i t}{θ^{2} + 2 θ}) {(1 - \frac{i t}{θ})}^{- 2}, i = \sqrt{- 1}$

$K_{X} (t) = \log (1 - \frac{(θ + 1) i t}{θ^{2} + 2 θ}) - 2 \log (1 - \frac{i t}{θ})$

Using the expansion $\log (1 - x) = - \sum_{r = 0}^{\infty} \frac{x^{r}}{r}$ , we get

$K_{X} (t) = - \sum_{r = 0}^{\infty} {(\frac{θ + 1}{θ^{2} + 2 θ})}^{r} \frac{{(i t)}^{r}}{r} + 2 \sum_{r = 0}^{\infty} \frac{{(\frac{i t}{θ})}^{r}}{r}$

$= 2 \sum_{r = 0}^{\infty} \frac{1}{θ^{r}} \frac{{(i t)}^{r}}{r} - \sum_{r = 0}^{\infty} {(\frac{θ + 1}{θ^{2} + 2 θ})}^{r} \frac{{(i t)}^{r}}{r}$

$= 2 \sum_{r = 0}^{\infty} \frac{(r - 1)!}{θ^{r}} \frac{{(i t)}^{r}}{r!} - \sum_{r = 0}^{\infty} {(\frac{θ + 1}{θ^{2} + 2 θ})}^{r} (r - 1)! \frac{{(i t)}^{r}}{r!}$

Thus the $r$ ^th cumulant of Garima distribution is given by

$K_{r}$ = coefficient of $\frac{{(i t)}^{r}}{r!}$ in $K_{X} (t)$

$= \frac{2 (r - 1)!}{θ^{r}} - \frac{(r - 1)! {(θ + 1)}^{r}}{{(θ^{2} + 2 θ)}^{r}}; r = 1, 2, 3, ...$

This gives

$μ_{1}^{'} = K_{1} = \frac{θ + 3}{θ (θ + 2)}$

$μ_{2} = K_{2} = \frac{θ^{2} + 6 θ + 7}{θ^{2} {(θ + 2)}^{2}}$

$μ_{3} = K_{3} = \frac{2 (θ^{3} + 9 θ^{2} + 21 θ + 15)}{θ^{3} {(θ + 2)}^{3}}$

$μ_{4} = K_{4} + 3 K_{2}^{2} = \frac{3 (3 θ^{4} + 36 θ^{3} + 134 θ^{2} + 204 θ + 111)}{θ^{4} {(θ + 2)}^{4}}$

Which the same are as obtained earlier.

Hazard rate function and mean residual life function

Let $X$ be a continuous random variable with pdf $f (x)$ and cdf $F (x)$ . The hazard rate function (also known as the failure rate function) and the mean residual life function of $X$ are respectively defined as

$h (x) = \lim_{Δ x \to 0} \frac{P (X < x + Δ x | X > x)}{Δ x} = \frac{f_{7} (x; θ)}{1 - F_{7} (x; θ)}$ (5.1)

and $m (x) = E [X - x | X > x] = \frac{1}{1 - F_{7} (x; θ)} \int_{x}^{\infty} [1 - F_{7} (t; θ)] d t$ (5.2)

The hazard rate function, $h (x)$ and the mean residual life function, $m (x)$ of Garima distribution are given by

$h (x) = \frac{θ (1 + θ + x)}{θ x + (θ + 2)}$ (5.3)

and $m (x) = \frac{θ x + θ + 3}{θ (θ x + θ + 2)}$ (5.4)

It can be easily verified that $h (0) = \frac{θ (θ + 1)}{θ + 2} = f (0)$ and $m (0) = \frac{θ + 3}{θ (θ + 2)} = μ_{1}^{'}$ .It is also obvious from the graphs of $h (x)$ and $m (x)$ that $h (x)$ is an increasing or decreasing function of $x$ , and $θ$ , where as $m (x)$ is a decreasing function of $x$ , and $θ$ . The graph of the hazard rate function and mean residual life function of Garima distribution are shown in Figures 2 & 3.

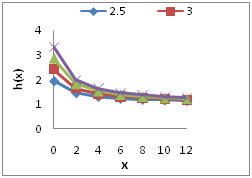
Figure 2 Graph of hazard rate function of Garima distribution for different values of parameter θ.

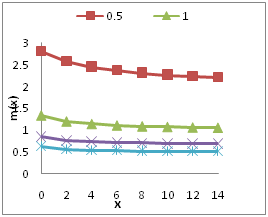
Figure 3 Graph of mean residual life function of Garima distribution for different values of parameter θ.

Stochastic orderings

Stochastic ordering of positive continuous random variables is an important tool for judging their comparative behavior. A random variable $X$ is said to be smaller than a random variable $Y$ in the

stochastic order $(X \leq_{s t} Y)$ if $F_{X} (x) \geq F_{Y} (x)$ for all $x$
hazard rate order $(X \leq_{h r} Y)$ if $h_{X} (x) \geq h_{Y} (x)$ for all
mean residual life order $(X \leq_{m r l} Y)$ if $m_{X} (x) \leq m_{Y} (x)$ for all $x$
likelihood ratio order $(X \leq_{l r} Y)$ if $\frac{f_{X} (x)}{f_{Y} (x)}$ decreases in $x$ .

The following results due to Shaked & Shanthikumar [6] are well known for establishing stochastic ordering of distributions

$X \leq_{l r} Y \Rightarrow X \leq_{h r} Y \Rightarrow X \leq_{m r l} Y$ (6.1)

$\underset{X \leq_{s t} Y}{⇓}$

The Garima distribution is ordered with respect to the strongest ‘likelihood ratio’ ordering as shown in the following theorem:

Theorem: Let $X$ $\sim$ Garima distributon $(θ_{1})$ and $Y$ $\sim$ Garima distribution $(θ_{2})$ . If $θ_{1} \geq θ_{2}$ , then $X \leq_{l r} Y$ and hence $X \leq_{h r} Y$ , $X \leq_{m r l} Y$ and $X \leq_{s t} Y$ .
Proof: We have

$\frac{f_{X} (x)}{f_{Y} (x)} = \frac{θ_{1} (θ_{2} + 2)}{θ_{2} (θ_{1} + 2)} (\frac{1 + θ_{1} + θ_{1} x}{1 + θ_{2} + θ_{2} x}) e^{- (θ_{1} - θ_{2}) x}$ $; x > 0$

Now

$\log \frac{f_{X} (x)}{f_{Y} (x)} = \log [\frac{θ_{1} (θ_{2} + 2)}{θ_{2} (θ_{1} + 2)}] + \log (\frac{1 + θ_{1} + θ_{1} x}{1 + θ_{2} + θ_{2} x}) - (θ_{1} - θ_{2}) x$

This gives $\frac{d}{d x} \log \frac{f_{X} (x)}{f_{Y} (x)} = \frac{θ_{1} - θ_{2}}{(1 + θ_{1} + θ_{1} x) (1 + θ_{2} + θ_{2} x)} - (θ_{1} - θ_{2})$

Thus for $θ_{1} \geq θ_{2}$ , $\frac{d}{d x} \log \frac{f_{X} (x)}{f_{Y} (x)} < 0$ . This means that $X \leq_{l r} Y$ and hence $X \leq_{h r} Y$ , $X \leq_{m r l} Y$ and $X \leq_{s t} Y$ .

Mean deviations

The amount of scatter in a population is measured to some extent by the totality of deviations usually from mean and median. These are known as the mean deviation about the mean and the mean deviation about the median defined by

$δ_{1} (X) = \int_{0}^{\infty} | x - μ | f (x) d x$ and $δ_{2} (X) = \int_{0}^{\infty} | x - M | f (x) d x$ , respectively, where $μ = E (X)$ and $M = Median (X)$ . The measures $δ_{1} (X)$ and $δ_{2} (X)$ can be calculated using the relationships

$δ_{1} (X) = \int_{0}^{μ} (μ - x) f (x) d x + \int_{μ}^{\infty} (x - μ) f (x) d x$

$= μ F (μ) - \int_{0}^{μ} x f (x) d x - μ [1 - F (μ)] + \int_{μ}^{\infty} x f (x) d x$

$= 2 μ F (μ) - 2 μ + 2 \int_{μ}^{\infty} x f (x) d x$

$= 2 μ F (μ) - 2 \int_{0}^{μ} x f (x) d x$ (7.1)

and

$δ_{2} (X) = \int_{0}^{M} (M - x) f (x) d x + \int_{M}^{\infty} (x - M) f (x) d x$

$= M F (M) - \int_{0}^{M} x f (x) d x - M [1 - F (M)] + \int_{M}^{\infty} x f (x) d x$

$= - μ + 2 \int_{M}^{\infty} x f (x) d x$

$= μ - 2 \int_{0}^{M} x f (x) d x$ (7.2)

Using p.d.f. (2.1) and expression for the mean of Garima distribution, we get

$\int_{0}^{μ} x f_{7} (x; θ) d x = μ - \frac{{θ^{2} μ^{2} + (θ^{2} + 3 θ) μ + (θ + 3)} e^{- θ μ}}{θ (θ + 2)}$ (7.3)

$\int_{0}^{M} x f_{7} (x; θ) d x = μ - \frac{{θ^{2} M^{2} + (θ^{2} + 3 θ) M + (θ + 3)} e^{- θ M}}{θ (θ + 2)}$ (7.4)

Using expressions from (7.1), (7.2), (7.3), and (7.4), the mean deviation about mean, $δ_{1} (X)$ and the mean deviation about median, $δ_{2} (X)$ of Garima distribution are obtained as

$δ_{1} (X) = \frac{(2 θ μ + θ + 3) e^{- θ μ}}{θ (θ + 2)}$ (7.5)

$δ_{2} (X) = \frac{2 {θ^{2} M^{2} + (θ^{2} + 3 θ) M + (θ + 3)} e^{- θ M}}{θ (θ + 2)} - μ$ (7.6)

Order statistics

Let $X_{1}, X_{2}, ..., X_{n}$ be a random sample of size $n$ from Garima distribution (2.1). Let $X_{(1)} < X_{(2)} < ... < X_{(n)}$ denote the corresponding order statistics. The p.d.f. and the c.d.f. of the $k$ ^th order statistic, say $Y = X_{(k)}$ are given by

$f_{Y} (y) = \frac{n!}{(k - 1)! (n - k)!} F^{k - 1} (y) {1 - F (y)}^{n - k} f (y)$

$= \frac{n!}{(k - 1)! (n - k)!} \sum_{l = 0}^{n - k} (\begin{matrix} n - k \\ l \end{matrix}) {(- 1)}^{l} F^{k + l - 1} (y) f (y)$

and

$F_{Y} (y) = \sum_{j = k}^{n} (\begin{matrix} n \\ j \end{matrix}) F^{j} (y) {1 - F (y)}^{n - j}$

$= \sum_{j = k}^{n} \sum_{l = 0}^{n - j} (\begin{matrix} n \\ j \end{matrix}) (\begin{matrix} n - j \\ l \end{matrix}) {(- 1)}^{l} F^{j + l} (y)$ ,

respectively, for $k = 1, 2, 3, ..., n$ .

Thus, the p.d.f. and the c.d.f of $k$ ^th order statistics of Garima distribution are given by

$f_{Y} (y) = \frac{n! θ (1 + θ + θ x) e^{- θ x}}{(θ + 2) (k - 1)! (n - k)!} \sum_{l = 0}^{n - k} (\begin{matrix} n - k \\ l \end{matrix}) \times {[1 - \frac{θ x + (θ + 2)}{θ + 2} e^{- θ x}]}^{k + l - 1}$

and

$F_{Y} (y) = \sum_{j = k}^{n} \sum_{l = 0}^{n - j} (\begin{matrix} n \\ j \end{matrix}) (\begin{matrix} n - j \\ l \end{matrix}) {(- 1)}^{l} {[1 - \frac{θ x + (θ + 2)}{θ + 2} e^{- θ x}]}^{j + l}$

Bonferroni and lorenz curves

The Bonferroni and Lorenz curves⁷ and Bonferroni and Gini indices have applications not only in economics to study income and poverty, but also in other fields like reliability, demography, insurance and medicine. The Bonferroni and Lorenz curves are defined as

$B (p) = \frac{1}{p μ} \int_{0}^{q} x f (x) d x = \frac{1}{p μ} [\int_{0}^{\infty} x f (x) d x - \int_{q}^{\infty} x f (x) d x] = \frac{1}{p μ} [μ - \int_{q}^{\infty} x f (x) d x]$ (9.1)

and $L (p) = \frac{1}{μ} \int_{0}^{q} x f (x) d x = \frac{1}{μ} [\int_{0}^{\infty} x f (x) d x - \int_{q}^{\infty} x f (x) d x] = \frac{1}{μ} [μ - \int_{q}^{\infty} x f (x) d x]$ (9.2)

respectively or equivalently

$B (p) = \frac{1}{p μ} \int_{0}^{p} F^{- 1} (x) d x$ (9.3)

and $L (p) = \frac{1}{μ} \int_{0}^{p} F^{- 1} (x) d x$ (9.4)

respectively, where $μ = E (X)$ and $q = F^{- 1} (p)$ .

The Bonferroni and Gini indices are thus defined as

$B = 1 - \int_{0}^{1} B (p) d p$ (9.5)

and $G = 1 - 2 \int_{0}^{1} L (p) d p$ (9.6)

respectively.

Using p.d.f. (2.1), we get

$\int_{q}^{\infty} x f_{7} (x; θ) d x = \frac{{θ^{2} q^{2} + (θ^{2} + 3 θ) q + (θ + 3)} e^{- θ q}}{θ (θ + 2)}$ (9.7)

Now using equation (8.7) in (8.1) and (8.2), we get

$B (p) = \frac{1}{p} [1 - \frac{{θ^{2} q^{2} + (θ^{2} + 3 θ) q + (θ + 3)} e^{- θ q}}{θ + 3}]$ (9.8)

and $L (p) = 1 - \frac{{θ^{2} q^{2} + (θ^{2} + 3 θ) q + (θ + 3)} e^{- θ q}}{θ + 3}$ (9.9)

Now using equations (9.8) and (9.9) in (9.5) and (9.6), the Bonferroni and Gini indices of Garima distribution (2.1) are obtained as

$B = 1 - \frac{{θ^{2} q^{2} + (θ^{2} + 3 θ) q + (θ + 3)} e^{- θ q}}{θ + 3}$ (9.10)

$G = - 1 + \frac{2 {θ^{2} q^{2} + (θ^{2} + 3 θ) q + (θ + 3)} e^{- θ q}}{θ + 3}$ (9.11)

Renyi entropy

Entropy of a random variable $X$ is a measure of variation of uncertainty. A popular entropy measure is Renyi entropy [8]. If $X$ is a continuous random variable having probability density function $f (.)$ , then Renyi entropy is defined as

$T_{R} (γ) = \frac{1}{1 - γ} \log {\int f^{γ} (x) d x}$

where $γ > 0 and γ \neq 1$ .

Thus, the Renyi entropy for the Garima distribution (2.1) is obtained as

$T_{R} (γ) = \frac{1}{1 - γ} \log [\int_{0}^{\infty} \frac{θ^{γ}}{{(θ + 2)}^{γ}} {(1 + θ + θ x)}^{γ} e^{- θ γ x} d x]$

$= \frac{1}{1 - γ} \log [\int_{0}^{\infty} \frac{θ^{γ} {(1 + θ)}^{γ}}{{(θ + 2)}^{γ}} {(1 + \frac{θ}{θ + 1} x)}^{γ} e^{- θ γ x} d x]$

$= \frac{1}{1 - γ} \log [\int_{0}^{\infty} \frac{θ^{γ} {(1 + θ)}^{γ}}{{(θ + 2)}^{γ}} \sum_{j = 0}^{\infty} (\begin{matrix} γ \\ j \end{matrix}) {(\frac{θ}{θ + 1} x)}^{j} e^{- θ γ x} d x]$

$= \frac{1}{1 - γ} \log [\sum_{j = 0}^{\infty} (\begin{matrix} γ \\ j \end{matrix}) \frac{θ^{γ + j} {(1 + θ)}^{γ - j}}{{(θ + 2)}^{γ}} \int_{0}^{\infty} e^{- θ γ x} x^{j + 1 - 1} d x]$

$= \frac{1}{1 - γ} \log [\sum_{j = 0}^{\infty} (\begin{matrix} γ \\ j \end{matrix}) \frac{θ^{γ + j} {(1 + θ)}^{γ - j}}{{(θ + 2)}^{γ}} \frac{Γ (j + 1)}{{(θ γ)}^{j + 1}}]$

$= \frac{1}{1 - γ} \log [\sum_{j = 0}^{\infty} (\begin{matrix} γ \\ j \end{matrix}) \frac{θ^{γ - 1}}{{(θ + 2)}^{γ}} \frac{Γ (j + 1)}{{(γ)}^{j + 1}}]$

Stress-strength reliability

The stress- strength reliability describes the life of a component which has random strength $X$ that is subjected to a random stress $Y$ . When the stress applied to it exceeds the strength, the component fails instantly and the component will function satisfactorily till $X > Y$ . Therefore, $R = P (Y < X)$ is a measure of component reliability and in statistical literature it is known as stress-strength parameter. It has wide applications in almost all areas of knowledge especially in engineering such as structures, deterioration of rocket motors, static fatigue of ceramic components, aging of concrete pressure vessels etc.

Let $X$ and $Y$ be independent strength and stress random variables having Garima distribution (2.1) with parameter $θ_{1}$ and $θ_{2}$ respectively. Then the stress-strength reliability $R$ of Garima distribution can be obtained as

$R = P (Y < X) = \int_{0}^{\infty} P (Y < X | X = x) f_{X} (x) d x$

$= \int_{0}^{\infty} f_{7} (x; θ_{1}) F_{7} (x; θ_{2}) d x$

$= 1 - \frac{θ_{1} [{(θ_{1} + θ_{2})}^{2} (θ_{1} θ_{2} + 2 θ_{1} + θ_{2} + 1) + 2 θ_{1} θ_{2} (θ_{1} + θ_{2}) + 2 θ_{1} θ_{2}]}{(θ_{1} + 2) (θ_{2} + 2) {(θ_{1} + θ_{2})}^{3}}$ .

Estimation of parameter

Maximum likelihood estimates (MLE)

Let $(x_{1}, x_{2}, x_{3}, ..., x_{n})$ be a random sample from Garima distribution (2.1). The likelihood function, $L$ of (2.1) is given by

$L = {(\frac{θ}{θ + 2})}^{n} \prod_{i = 1}^{n} (1 + θ + θ x_{i}) e^{- n θ \bar{x}}$

The natural log likelihood function is thus obtained as

$\ln L = n \ln (\frac{θ}{θ + 2}) + \sum_{i = 1}^{n} \ln (1 + θ + θ x_{i}) - n θ \bar{x}$

Now $\frac{d \ln L}{d θ} = \frac{2 n}{θ^{2} + 2 θ} + \sum_{i = 1}^{n} \frac{1 + x_{i}}{1 + θ + θ x_{i}} - n \bar{x} = 0$

where $\bar{x}$ is the sample mean.

The maximum likelihood estimate, $\hat{θ}$ of $θ$ is the solution of the equation $\frac{d \log L}{d θ} = 0$ and so it can be obtained by solving the following non-linear equation

$\sum_{i = 1}^{n} \frac{1 + x_{i}}{1 + θ + θ x_{i}} + \frac{2 n}{θ^{2} + 2 θ} - n \bar{x} = 0$ (12.1.1)

Method of moment estimates (MOME)

Equating the population mean of the Garima distribution to the corresponding sample mean, the method of moment estimate (MOME) $\tilde{θ}$ , of $θ$ can be obtained as

$\tilde{θ} = \frac{(1 - 2 \bar{x}) + \sqrt{4 {\bar{x}}^{2} + 8 \bar{x} + 1}}{2 \bar{x}}; \bar{x} > 0$ (12.2.1)

A numerical example

In this section the goodness of fit of the Garima distribution has been discussed with an example from behavioral science. The data is related with behavioral sciences, collected by Balakrishnan N et al. [9]. The scale “General Rating of Affective Symptoms for Preschoolers (GRASP)” measures behavioral and emotional problems of children, which can be classified with depressive condition or not according to this scale. A study conducted by the authors in a city located at the south part of Chile has allowed collecting real data corresponding to the scores of the GRASP scale of children with frequency in parenthesis, which are:

19(6)	20(15)	21(14)	22(9)	23(12)	24(10)
25(6)	26(9)	27(8)	28(5)	29(6)	30(4)
31(3)	32(4)	33	34	35(4)	36(2)
37(2)	39	42	44

In order to compare distributions, $- 2 \ln L$ , AIC (Akaike Information Criterion), AICC (Akaike Information Criterion Corrected), BIC (Bayesian Information Criterion),K-S Statistics ( Kolmogorov-Smirnov Statistics) for above data set have been computed and presented in Table 3. The formulae for computing AIC, AICC, and BIC are as follows:

$A I C = - 2 \ln L + 2 k$ , $A I C C = A I C + \frac{2 k (k + 1)}{(n - k - 1)}$ , $B I C = - 2 \ln L + k \ln n$

The best distribution is the distribution which corresponds to lower values of $- 2 \ln L$ , AIC, AICC, and BIC.

It can be easily seen from above table that the Garima distribution is better than Aradhana, Sujatha, Akash, Shanker, Lindley and exponential distributions for modeling behavioral science data and thus Garima distribution should be preferred over Aradhana, Sujatha, Akash, Shanker, Lindley and exponential distributions for modeling behavioral science data.

Model	ML Estimate	$- 2 \ln L$	AIC	AICC	BIC
Garima	0.05317	188.32	190.32	190.35	193.23
Aradhana	0.11557	989.49	991.49	991.52	994.40
Sujatha	0.11745	985.69	987.69	987.72	990.60
Akash	0.11961	981.28	983.28	983.31	986.18
Shanker	0.07974	1033.10	1035.10	1035.13	1037.99
Lindley	0.07725	1041.64	1043.64	1043.68	1046.54
Exponential	0.04006	1130.26	1132.26	1132.29	1135.16

Table 3 MLE’s,-2ln L, AIC, AICC, and BIC of Garima, Aradhana, Sujatha [4], Akash [2], Shanker [1], Lindley [5] and exponential distributions

Conclusion

A one parameter lifetime distribution named, “Garima distribution” has been proposed and studied. Its mathematical properties including shape, moments, skewness, kurtosis, hazard rate function, mean residual life function, stochastic ordering, mean deviations, order statistics, Bonferroni and Lorenz curves, Renyi entropy and stress-strength reliability have been discussed. The condition under which Garima distribution is over-dispersed, equi-dispersed, and under-dispersed are presented along with the conditions under which Sujatha, Aradhana, Akash, Shanker, Lindley and exponential distributions are over-dispersed, equi-dispersed and under-dispersed. The method of moments and the method of maximum likelihood estimation have also been discussed for estimating its parameter. Finally, a numerical example from behavioral science has been considered for the goodness of fit of Garima distribution and the fit has been compared with Sujatha, Aradhana, Akash, Shanker, Lindley and exponential distributions. The goodness of fit of the Garima distribution shows that it is an important model for modeling behavioral science data.

NOTE: The paper is named in loving memory of my niece Garima Satypriya, daughter of my respected brother Prof. Uma Shanker, Department of Mathematics, K.K College of Engineering & Management, Biharsharif, Nalanda, India.