As cultural issues have been acknowledged as one of the most important aspects in improving patient safety,^1-4 many resources have been invested to tap into the safety culture from a small clinic setting to even a nationwide health care setting. The first step is, of course, accurately measuring safety culture, which plays an important role not only in understanding the topography of safety culture, but also in evaluating the effectiveness of endeavors for safety improvement. Consequently, various instruments to measure safety culture have been developed and utilized.^5-8 Among them, the Safety Attitudes Questionnaire (SAQ) is one of the most frequently used instruments^5,6,9 and has already been translated into several languages for various countries.^10-15 Jeong et al. developed the 34-item Korean version of SAQ (SAQ-K)¹⁶ and devised novel approaches for analyzing its results using empirical Bayes methods.^9,17,18 Like the original version, SAQ-K consists of six distinct domains, the definitions of which are described in Table 1.⁸ SAQ-K has been thoroughly validated and widely used in health care organizations in Korea.

Despite the successful application of such instruments in gauging patient safety culture in health care, we have to admit that those safety culture instruments, including SAQ-K, should be revalidated for several reasons. In most cases, the critical part of the survey questionnaire validation process has been conducted using confirmatory factor analysis (CFA).¹⁹ The problem here is that CFA can and should only be used for continuous responses, not for categorical responses such as a 5-point Likert scale, because CFA is basically a linear regression model. Therefore, it cannot appropriately deal with the errors in a measurement model for dichotomous or categorical responses—errors that can neither be normally distributed nor have constant variance. In addition, in the CFA paradigm, the probability of choosing an option for an item can go out of bounds²⁰ Simply put, validating a Likert scale-based instrument with CFA is theoretically incorrect. Unfortunately, however, the original SAQ and all its variants, including SAQ-K, measure responses on a 5-point Likert scale (1= disagree strongly, 2= disagree slightly, 3= neutral, 4= agree slightly, 5= agree strongly) and then convert them to a scale from 0 to 100, with 25-point intervals. In all honesty, we might have misused the continuous response targeted method for categorical variables based on the unfounded assumption that the Likert scale would behave just like continuous response.

Another issue in the everyday use of SAQ thus far is that we use the simple mean domain score (arithmetic mean of the item scores in a domain), from 0 to 100, which is the method that the original SAQ rubric suggests. Although it is easy to calculate, this approach implicitly assumes that items are $\tau$ (“tau”) equivalent, which means all the items in a domain are equally important; in CFA terminology, they should share similar factor loadings. If this assumption does not hold, then we should use a factor score that places more weight on the items with larger load in gand less weight on items with smaller loading to prevent overvaluing or undervaluing items. In this way, we can obtain more reliable estimates.²¹ Now, we are trapped in a catch-22 situation: When we try to prove that $\tau$ equivalence is satisfied or to use the factor score approach, weneed to runa CFAfirst to calculate the loadings. However, CFA is not an appropriate method for categorical responses, at least not by definition. It seems like there is no way out. How can we escape this dilemma?

We propose using the item response theory (IRT)—specifically, the graded response model (GRM)—to understand SAQ’s item properties and obtain adjusted domain scores that are logically more sound. Developed by Same jima,²² the idea of GRM is also known as the cumulative logit model and can effectively handle the categorical responses as well as enable us to understand the psychometric properties of both the whole instrument and each item.

Fayers defined IRT as “a model-based measurement, also known as latent theory, in which trait level estimates depend on both persons’ responses and on the properties of the items that were administered”²³ For most readers, this definition is a bit complicated, and fully understanding the behind-the-scenes logic is even more complicated. Therefore, we do not use jargon like phi-gamma psychophysics,²⁴ nor do we describe detailed mathematical formulas for IRT parameter estimation here. Rather, we show how to interpret the key element of IRT GRM into plain language through a simple illustrative example, which will help the readers understand the rest of this article.

An illustrative example of IRT GRM

Assume we are analyzing the property of an item called K to estimate the level of a certain latent trait, which is an unobservable characteristic of a person, such as perception of teamwork climate (TC) on SAQ. Item K was measured on a 5-point Likert scale (1 = disagree strongly; 5 = agree strongly). We describe the IRT GRM perspective in Figures 1 & 2, where the level of the latent trait is denoted on the x axis in a scale with a mean of 0 and a standard deviation (SD) of 1. At this point, it should be understood that, unlike the scale in the classic test theory (CTT) paradigm, this scale with a mean and SD in the IRT paradigm is not sample specific; in other words, even when the instrument is administered to other groups, the items behave the same way with the same item properties, yielding comparable scores for the groups. This is called parameter invariance, and it is one of the most important and most frequently misunderstood assumptions of IRT.

Returning to the example, we first add meanings to Figure 1 that clearly shows us the essential nature of GRM, the cumulative logit model: i) y axis is the probability of choosing a certain response category (option) equal to or higher than the category versus lower than the category (e.g., category 2, 3, 4, or 5 versus category 1), and ii) there are multiple S-shaped curves due to multiple categories as an option of an item, contrary to the single line (not curved) for an item of the CFA paradigm.

Figure 1 Boundary characteristic curves (BCC) for item K

Although not explicitly, an important characteristic of IRT is embedded in Figure 1, which is called the discrimination parameter (denoted as “a”). It refers to how fast the probability of choosing an option category is changing near the value of the difficulty parameter. We can understand this as a differential coefficient of the curves at the 50% probability; the higher this parameter is, the more sensitively an item can detect a difference in a latent trait.

When we run the IRT GRM, what is usually returned from most statistical software is a form as shown in Table 2 (information on statistical significance is omitted here). Note that only one discrimination parameter exists, unlike multiple difficulty parameters. This is a convention of GRM.

In addition, we can find the probability of which category (option) will be answered by a person with a certain level of latent trait. Such information can be depicted in the form of a graph called category characteristic curves (see Figure 2).The interpretation is rather intuitive: A respondent with a latent trait lower than -2.15 is likely to respond 1, a respondent with a latent trait ranging between -2.15 and -1.37 is likely to respond 2, and so on.

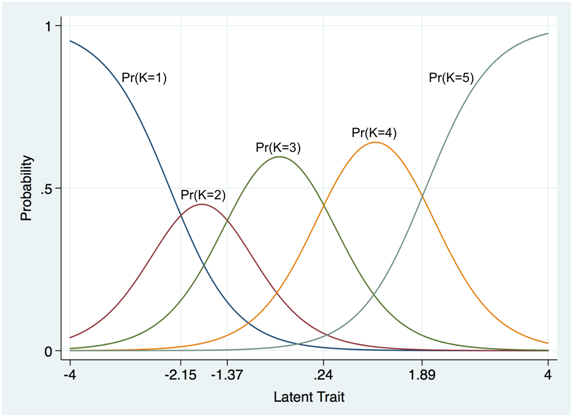
Figure 2 Category characteristic curves for item K

Because GRM is for ordered responses, the order of curves in the BCC or CCC style plots is always arranged from category one (left) to five (right) for a 5-point Likert scale; therefore, the category for which a curve stands will no longer be indicated in this article, if no specific reason to do so exists.

This example with multiple curves and uneven intervals between them, provides empirical evidence that the continuous response assumption of CFA may not work well for categorical response; it also shows why we actually can and should take advantage of the IRT framework for a non-continuous response. We use many other features of IRT in this article, but the discussion thus far offers a sufficient background for understanding the content of this study, even if the reader is not accustomed to an IRT paradigm.

Based on the background provided, this study aims to accomplish the following:

1. to re-validate SAQ-K with IRT GRM, unraveling both the item-level and instrument-level properties that have not yet been thoroughly investigated; and
2. to calculate new estimates of SAQ-K scores for each domain based on the IRT approach and compare them with the scores based on the simple arithmetic mean approach that the original SAQ rubric suggested.

Although we followed an IMRaD structure (Introduction, Methods, Results, and Discussion), the contents are somewhat blended; in particular, some paragraphs on methods and discussions are located in the results section. This is intentional. We tried to help readers who are not used to the IRT framework to fully understand the contents of this article.

We used the same dataset analyzed to validate SAQ-K; the data were collected in a large metropolitan hospital in Seoul from October through November 2013.Detailed information as to survey administration can be found in our previous articles^16,18

To examine the psychometric properties of SAQ-K with IRT GRM, we first obtained discrimination (a) and difficulty (b) parameters for each of the SAQ-K items. To help understand how the SAQ-K items may behave, we roughly classified the items into four distinct patterns and plotted their category characteristic curves (CCC) in Figure 3, which shows the probabilities of choosing a certain response category of the Likert scale through the latent trait continuum (please refer to Figure 2 for a better understanding).

Next, we tried to reveal the characteristics of the instrument as a whole; the expected domain score against latent trait was calculated by summing up the expected score of each item at every point of the latent trait level of each domain. By depicting this information in the form of test characteristic curve (TCC) in the traditional 0 to 100 SAQ scoring system, we tried to understand which score we could expect from SAQ-K for a person with a certain trait level on the current scoring scheme.

We also visited the amount of information that each item possesses. First, we plotted item information along the latent continuum in a format called item information function (IIF). Then, by adding up the IIF of items in each domain, we obtained a domain-level test information function (TIF), which shows how precisely SAQ-K can estimate the level of a respondent’s latent trait. More specifically, TIF helps us decide which region on the latent trait continuum can be estimated most precisely or most poorly—in other words, where the holes are.

Lastly, we predicted a respondent’s latent trait level of each domain by using empirical Bayes (EB) method in the IRT sense and calculated the correlation coefficient between the EB estimates and traditional arithmetic mean SAQ domain scores that did not take into account the $\tau$ equivalence issue. We also visualized the correlation with a scatter plot with linear regression and locally weighted scatter plot smoothing (LOWESS) lines for each domain.

Running IRT GRM, we used mean-variance adaptive Gauss-Hermite quadrature for numerical integration, with seven integration points that were computationally efficient and provided results with enough precision. For all analyses, Stata 14.1 (Stata Corp., College Station, Texas) was used.

Characteristics of respondents

Of the 1,381 questionnaires returned, we analyzed 1,142 questionnaires that contained no missing values. We did this list-wise deletion to compare the two different approaches of CFA and IRT fairly; that is to say, IRT models can bear missing values, but CFA cannot. Table 3 shows the characteristics of the respondents, including gender, work year, and job type. The majority of respondents were female nurses—the composition that reflects the general situation of the Korean health care system.

Psychometric properties of SAQ-K items

The properties of all 34 items of SAQ-K, difficulty (b), and discrimination (a) are described in Table 4. The “Info rank” column will be explained in a later section. From now on, the item ID is used to describe the results.

For discrimination, JS3 showed the highest value (4.22) while WC1 showed the lowest (1.12), yielding a greater than three-times difference. Although we do not describe each value of difficulty parameters, it is worth noting that not every item shows that the four difficulty parameters were evenly distributed around zero. In addition, items within the same domain do not share the same pattern in parameter distribution. In order to help readers better understand, we classified the CCC of all 34 items into four distinct patterns (Figure 3). This classification was done by the authors’ subjective analysis, not based on any statistical pattern analysis, which is beyond the scope of this study.

Note: x-axis: latent trait; y-axis: probability of answering a certain category.

Figure 4 Graphical display of the four patterns of category characteristic curves with exemplary items.

Test characteristics of SAQ-K by domain

Figure 4 shows the scores we can expect from respondents who possess different levels of the latent trait by each domain. To illustrate, for the TC domain, respondents with an above average latent trait level are likely to score higher than 65.8. For this expected score for individuals with an average latent trait, we can see significant differences across domains: 66.67 (SC), 59.3 (JS), 70.63 (SR), 61.5 (PM), and 55.5 (WC).

By extension, we can apply the 95% interval to this graph. Because the scale of latent trait is a mean of 0 and SD of 1, the 95% interval means the latent trait level ranges from -1.96 to 1.96. Again, using the TC domain as an example, we can expect 95% of randomly selected respondents to score between 30.2 and 94.8. Instead of providing those numbers here, we present a graphical summary of the mean and 95% expectation score (Figure 5). We can easily find a considerable amount of discrepancy across domains.

Note: x-axis: latent trait; y-axis: expected SAQ-K domain score in the traditional 0 to 100 SAQ scoring system.

Figure 4 Test characteristic curves by SAQ-K domain

Amount of information by item and domain

Figure 6 shows the amount of information an item and domain convey. In the IRT realm, the information is the conceptualization of the precision and reliability of the item and the instrument. That is to say, the high information region (where a curve stays high) has more capacity to measure an individual’s latent trait level with more precision and with smaller error. The left pane shows the information amount of each item against the latent trait level. There are too many items and crisscrossing, so we did not indicate the item ID on the plot. Instead, we arbitrarily chose a trait level X at which item information curves were not too crowded and numbered the curves from top to bottom. This rank is listed in the last column (Info rank) of Table 3.

Figure 5 Expected average scores and 95% intervals by SAQ-K domain

Because SAQ-K consists of a 5-point Likert scale, we do not have a unimodal or symmetric item information function (IIF); instead, each category of an item provides its own information, leading to the multimodal curves with four peaks for each (the use of five categories means that there are four thresholds between category pairs in a cumulative setting). Note that for most domains except for JS, IIFs stayed high compared to latent trait levels even lower than -2, but in the opposite direction, IIFs generally began to drop even before 2, suggesting that the items provide less information in the high latent trait region than in the lower latent trait region.

It is also worth noting that the information amount varies significantly across different items. SR, PM, and WC domains are great examples. Two items in SR (SR1 and SR2), two items in PM (PM2 and PM7), and WC1 showed much lower IIFs than other items in each domain, suggesting that those items did not add much information to the whole domain in which they were included. The Info rank column in Table 3 provides details on which item showed low or high IIF.

In Figure 6, the plots of the right pane are called test information function (TIF) and depict the information amount of six domains (solid line), each of which was obtained by summing up the IIFs on the left pane. Thus, generally a domain with more items shows a higher TIF. The dashed lines are the standard error of the latent trait estimates and provide almost mirror images of information curves in a vertical direction, which makes sense in that a precise measurement means a smaller error. TIFs of TC and SC showed their peaks from around -3 to 1.8; outside these regions, the curves dropped. JS, SR, and PM showed a similar peak at the upper value, around 1.8, but the lower value of the peak was a bit higher, around-2, which means the precision is high in a narrower range. WC showed a relatively wide plateau in TIF, extending the upper peak to around 2. Note that not a single domain showed a flat and high TIF, and outside a certain range the TIF curve dropped while the standard error curve surged, suggesting that the amount of information that the items and test can provide varied considerably along the latent trait.

Comparing IRT approach and traditional arithmetic mean approach in obtaining SAQ-K domain estimates

As described in an earlier section, the six SAQ domain scores were obtained by computing the arithmetic mean of items of each domain without considering the weighting on the items. On the other hand, IRT GRM calculated empirical Bayes (EB) estimates of latent trait level by taking into account parameters of each item. We applied both approaches and calculated the correlation coefficient of each domain (Table 5). The correlation coefficients for all six domains were very high and statistically significant.

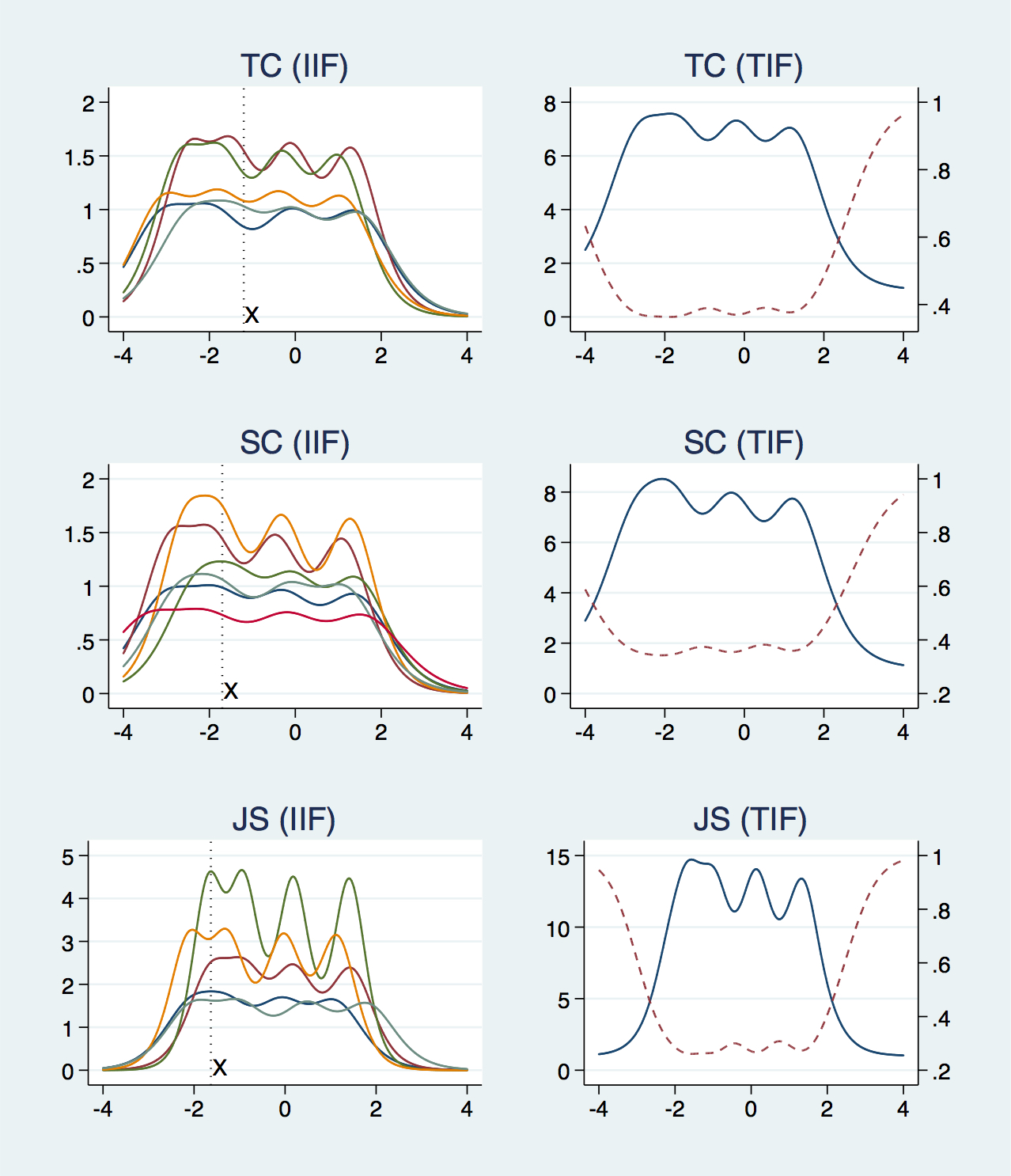
Note: x-axis: latent trait; y-axis (left): amount of information; y-axis (right): standard error; solid line: information amount; dashed line: standard error.

Figure 6A Item information function (IIF) and test information function (TIF) by SAQ-K domain.

Note: x-axis: latent trait; y-axis (left): amount of information; y-axis (right): standard error; solid line: information amount; dashed line: standard error.

Figure 6B Item information function (IIF) and test information function (TIF) by SAQ-K domain.

We then plotted the estimates from the two approaches in a two-way scatter graph format, which tells us more information that is a bit different from the very high correlation coefficients discussed earlier. Generally, all domains showed a linear relationship between the two approaches, but unlike the EB estimates, which showed continuous characteristics (see y values of the observations), traditional arithmetic means showed a discontinuous nature due to the categorical characteristics of the Likert scale that SAQ uses. More importantly, a certain domain score from the traditional approach corresponded to many different EB estimates from the IRT approach. This phenomenon might arise from the issue of $\tau$ equivalence. For example, with the arithmetic mean approach, a person who chose answers 2, 3, 3, 3, and 4 for the first through fifth items in the TC domain might yield a mean score of 3; another person who chose 4, 3, 3, 3, and 2 for the same items would have the same mean score, 3. However, if the amount of information or importance of the first and the last items differed, and such a difference was legitimately compensated, those two people’s domain scores should be different. This is exactly what the graphs shows: There are many combinations of answers of the items, and those combinations may yield the same arithmetic mean, but once the importance of each item is taken into consideration, the EB estimates of the latent trait can and should vary across the combinations that have the same arithmetic mean, as shown in Figure 7.

If we observe the plots horizontally, this phenomenon is even more clearly observed. For example, for SR on the latent trait level (y-value), 0, the traditional arithmetic score expands from almost 50 to 75, which means that people with the same SR trait level can be considered very differently in the arithmetic mean paradigm.

Note: x-axis: traditional arithmetic mean of SAQ domain scores; y-axis: latent trait level from IRT; solid line: linear regression line; dashed-line: LOWESS smothering line.

Figure 7 Scatter plot of traditional SAQ scores and IRT-based estimates of latent traits and fitted lines.

The primary purpose of applying IRT, besides handling the CFA’s issues in dealing with categorical responses, is to develop scale or metric that assigns values to the latent trait. Readers who are relatively new to the IRT paradigm might find this process a bit hard to admit, but actually it is not. Scale development begins by choosing an anchor point and then deciding the size of the unit, indicating the distance from the anchor point. Such a process may seem arbitrary, but it has always been around us. For example, the freezing point of water is 32° and the boiling point is 212° on the Fahrenheit scale, with 180 intervals between the two points, which serve as the anchor points while the intervals are the measurement unit. In the Celsius scale, the same freezing point and boiling point are 0° and 100°, respectively, resulting in 100 equal intervals between them.^23,25 The point here is that we arbitrarily but systematically assign values to the anchor points and then decide how many intervals should occur—in other words, the resolution of the unit in measuring the target phenomenon. As such, although we used a scale with a mean of 0 and a standard deviation of 1 for the latent trait in this article, we can always transform the scale to a traditional 0 to 100 scale of SAQ, maintaining the strengths of the IRT approach.

Along the same lines, one of the most fascinating properties of the IRT scale is that the latent traits and item parameters are expressed in the same metric: the so-called conjoint scale. To illustrate, the difficulty parameters (b) of the items are referenced to the very same scale for respondents’ latent trait (e.g., if b is -2, then b is located at -2 S Don the latent trait continuum).Thus, any transformation of a scale into another one does not cause a problem as long as the transformation is applied to both latent trait and item parameters simultaneously. Naturally, unlike the classic test theory, we do not need a comparison to the sample who took the test together to estimate a subject’s latent trait level. In the IRT paradigm, a person’s information and item properties do not depend on each other; therefore, we just use the item parameters to obtain the latent trait level of each person because the probability of how an item behaves at each point of the latent trait has already been on the shelf since the development and testing of the item.^26,27

These ideas boil down to the following crucial characteristic of IRT, called parameter invariance, which is described as “when an IRT model fits the data exactly in the population, then the estimated item parameters should be the same, within sampling error, regardless of what sample the data were derived from, and the estimated person latent traits should be the same regardless of what items they are based on”.²⁸ This parameter invariance provides us with the utmost practical usefulness. Simply put, we can use the items with any groups regardless of the difference among groups; if needed, even different instruments can be administered to different respondents. For some of the readers, this parameter invariance might not make much sense, but they probably have already gone through such test instruments. Many computer-adaptive tests, such as Test of English as a Foreign Language (TOEFL) and Graduate Record Examinations (GRE), are great examples.^29,30 Test takers of those exams can choose the date and time of their test, which means their scores are independent of other test takers (no comparison with others). Each test taker is presented with different item sets, which means as long as we know the item properties, we can measure the subject’s ability; we do not need to administer the same items to all subjects.

Although there are other aspects of IRT, such as uni-dimensionality or local independence, describing all of them are beyond the scope of this article. Let us return to the results of this study.

Picking up the above-mentioned scale issue, we revisit the problem of the current arithmetic mean-based scoring system for each domain used in almost all cases of SAQ use. Most frontline personnel who use SAQ think of the current scoring as an absolute value—that is to say, they believe scores that were generated in the traditional way can be directly compared across different domains. Therefore, if mean scores of subjects of a certain domain are clumped around a certain value and another domain shows a wide spread, people interpret this different distribution patterns in domain scores as the cultural characteristics of the target population who took the survey, which is the phenomenon we want to measure. However, by reviewing the test characteristic curves (TCC) in Figure 4, we can see that this approach may have a serious flaw. In the current arithmetic scoring system, each domain has its own expected score distribution as emphasized in Figure 5. Therefore, what we thought of as hospitals’ safety culture profile may actually come from instrument characteristics, not from respondents’ characteristics. In addition, many hospitals including Johns Hopkins, trace the temporal changes in SAQ scores.³¹ They frequently set a certain threshold value of change, such as 20, and if a certain domain score drops more than that, it is interpreted as a red flag. However, as TCC effectively demonstrates, the sensitivity of the traditional domain score on the change in latent trait varies significantly. For example, the 95% range of expected score in the JS domain spans from 13.1 to 95.6, which was much wider than that of WC (from 24.56 to 85.38). This means that the same amount of change in the latent trait level of JS is reflected as a larger change in SAQ score than that of WC in traditional SAQ scoring (as Figure 4 demonstrates, TCC of JS is steeper). Again, if this holds, what we have regarded as safety culture scores might have been the mixture of what we really wanted to measure and the test characteristics should not have been intervened or at least should have been canceled out.

In Figure 6, the IIF and TIF provide rich information in designing and modifying the test instrument. Let us discuss TIF first. As the sum of individual item information in IIF, TIF allows us to understand which region on the latent trait can or cannot be measured precisely—in other words, the size of error in the region. If we want an instrument targeting hospitals with a high safety culture, we might not need much information in the lower latent trait level. In this case, we probably want to remove some items focusing on the low trait level and add items for the high trait level to improve the precision at the high latent trait level. On the other hand, if the instrument is supposed to be generic and will be administered to all hospitals, then we prefer a relatively flat TIF to measure the latent trait along the entire range equally well. Therefore, if there is a so-called hole, the low information region along the latent trait continuum, we can add an item or two to make up for the hole and improve precision of the specific region. Therefore, the IIF’s information can serve as the basis for this instrument modification. In addition, more often than not, we need to remove some items due to, for example, respondents’ time constraints. The decision about which item should be taken out first can be helped by IIF; as in the left pane of Figure 6, some items clearly showed a very low IIF curve compared to other items in the domain, which means they do not contribute much to the information of the domain. Taking out those with low information function items and observing the change in TIF would probably be a logical process in controlling the number of items of the instrument.

We already raised concerns from the comparison between empirical Bayes (EB) estimates based on IRT and the traditional domain scores by arithmetic mean. We think a more important issue is not just the compatibility between them, but rather how SAQ scores are currently being used. In order to focus on the psychometric properties of SAQ, we mainly used scores, whether in the form of EB estimates or arithmetic mean. In many cases, however, SAQ scores are interpreted in the concept of “percent agreement”—that is, the percentage of respondents whose mean domain score is equal to or higher than 75 (the level of “agree slightly” in a Likert scale of SAQ). This approach is very meaningful, showing how the safety culture is spread among the respondents, health care professionals in a certain clinical area, or even a hospital. However, if we recall, a single latent trait score from IRT corresponds to a range of arithmetic mean scores; for example, for all six domains, the latent trait level 0 corresponded to around 60–80 of the traditional arithmetic mean score (refer to the discussion around Figure 7). Considering this, the problem becomes obvious. Certainly, for a group of respondents who share the same latent trait level, some of them might be classified as “those who agree,” whereas others might not. This phenomenon could be thought of as misclassification bias, which seriously undermines the validity of the survey.

In addition, this percent agreement approach basically reduces the resolution of the data to a dichotomized form; thus, the variance of scores cannot be addressed, and information on the score distribution, such as score change in a certain trait region (e.g., score change from 20 to 70), can easily be ignored. Regardless of which approach is used between traditional mean or IRT, this issue from percent agreement-based interpretation does exist. Therefore, more debate on this is required.

Finally, we also see the potential of IRT in national and international collaboration to improve patient safety. SAQ is certainly not the only safety measurement instrument; several other instruments, some of which have been developed by the hospitals themselves, are being used. Unfortunately, there was no way to combine those instruments and compare the results across hospitals or countries. However, using the IRT approach, items’ innate properties are revealed, and if those multiple instruments share a few core items, then we can merge the instruments to yield all the item properties on a single latent trait scale, which is a sharp contrast to the classic test theory (CTT). Indeed, this idea has been used in various fields, such as developing a new instrument for dementia patients by combining a few different instruments.³² Although the method is much more complicated, multi-group studies even at the country level have also been tried in other industries.³³ The safety culture instrument deserves such efforts, as such an endeavor will save lives globally.