eISSN: 2378-315X


Flexible regression models, such as fractional polynomial models and spline regression models, offer a rich class of models for linear and nonlinear dose-response relationships in epidemiology and clinical trials. In this paper, we consider first and second order fractional polynomials, and spline regression models to estimate the combined trend coefficients from dose-response models for cancer risk and exposure to low to moderate dose arsenic. The combined relative risks of bladder cancer and lung cancer are predicted for a sequence of low to moderate dose levels of arsenic from each model. Best-fit fractional polynomial models generate non-significant relative risks of both bladder cancer and lung cancer from low to moderate dose of arsenic levels in the range of 3 to 100 microgram per liter. The synthesis of results suggests that there is no or minimal risk of both bladder and lung cancer from dose-to-moderate lose arsenic exposure.
Keywords: arsenic, flexible regression models, spline regression models, cancer, carcinogenicity
Epidemiological studies on arsenic exposure through drinking water conducted in arsenic endemic regions of the world provide clear evidence of cancer risks at high-dose levels. Fortunately, very few humans are exposed to high dose levels. Much more common is exposure to low to moderate dose levels where evidence of carcinogenicity is mostly inconclusive. For example, a meta-analysis conducted by Chu & Crawford-Brown1 found a small but measurable increase in the risk of bladder cancer from arsenic exposure through drinking water at 10 ppb. These results are 10 times lower than those extrapolated by the NRC.2 However, Brown1 argues that problems with their methodology and analysis mean that their results may not be reliable. Mink et al.3 replicated Chu & Crawford-Brown’s1 results, finding a generally weak and statistically insignificant relationship between low-dose exposure to arsenic and bladder cancer. Likewise Begum et al.4 found a generally weak relationship between bladder and lung cancer and exposure to low-dose arsenic via drinking water. Other than the NRC,2 the combined results from these studies find no statistically significant dose-response relationship under the assumption of linear models for the logarithm of relative risks and levels of exposure to arsenic.
These meta-analysis studies on arsenic exposure and disease risk assume linear exposure-response models. The linearity assumption for the logarithm of relative risks and levels of exposure to arsenic is overly simplified and is not adequate to capture the local structure accurately. This article applies fractional polynomial and cubic spline regression models in order to capture the shapes of the exposure-response relationships between both bladder and lung cancer risk and exposure to low to moderate dose arsenic. We consider low to moderate dose levels with concentrations from near 0 to 300µg/l. We also consider more recent studies on low to moderate dose exposure to arsenic and the risk of bladder and lung cancer. These flexible models are used to identify a combined general exposure-response relationship for the logarithm of relative risk and the levels of exposure to arsenic. The primary objective of this study is to predict overall risks of bladder and lung cancers by combining findings from systematically selected studies on these cancers under both linear and non-linear modeling assumptions. We predict overall risks of bladder and lung cancers for a series of exposure levels from the best fitting models.
Though flexible regression models have been used to combine results in other epidemiological studies, such as alcohol consumption and all-cause mortality by Bagnardi,5 this is the first application to low to moderate dose arsenic consumption and the risk of internal cancers. This article is organized as follows: section 2 considers the systematic review of the bladder and lung cancer studies, section 3 discusses the fractional polynomials and the spline regression models, section 4 explains the results, and section 5 contains our conclusion and discussion.
Systematic reviews are carried out to select both bladder and lung cancer studies and exposure to low to moderate levels of arsenic through ingestion. Flowcharts of the step-by-step study selection procedure are presented in (Figure 1 & Figure 2).
We searched the Medline database with four arsenic search terms: arsenic, arsenite, arsenate, arsenicals and eight bladder cancer search terms: bladder cancer, transitional cell carcinoma of the bladder, urothelial cancer, urinary tract cancer, bladder neoplasm, urinary bladder neoplasm or urinary bladder cancer. Using these search terms, we identified 273 studies published before November 24, 2014 (Figure 1). We screened titles/abstracts of 222 studies. Of these, we reviewed the full text for 68 studies that met our selection criteria (Figure 1). Of these, 12 bladder cancer studies6-17 met all the inclusion criteria. Inclusion criteria were set as checkpoints which include
For lung cancer, we searched the Medline database using four arsenic keywords: arsenic, arsenite, arsenate, arsenicals and seven lung cancer search terms: lung cancer, lung neoplasm, small cell lung carcinoma, non-small cell lung carcinoma, bronchioloalveolar carcinoma, bronchiectasis, and bronchorrhea. Using these terms, we identified 461 studies published before November 24, 2014 (Figure 2). We screened titles/abstracts of 342 studies. Of these, we reviewed full text articles for 32 studies. Of these, 11 lung cancer studies17-27 met all the inclusion criteria.
Of the studies that fit the inclusion criteria, several included the same study populations. For example, Ferreccio et al.25 and Ferreccio et al.22 are from the same case-control study in northern Chile. To avoid double counting, we only included Ferreccio et al.22 Smith et al.26 uses the Ferreccio et al.22 data in their analysis. Therefore, we did not include Smith et al.26
Likewise, Steinmaus et al.17 and Steinmaus et al.27 analyze data from the same case-control study. To avoid double counting, we only include Steinmaus et al.17 because it includes a broader range of exposure levels. Avoiding double counting by dropping these studies means that eight lung cancer studies remain in the meta-analysis.
Summary of the included bladder and lung cancer studies: Table 1 summarizes the twelve bladder cancer studies and Table 2 summarizes the eight lung cancer studies. These tables list authors of each study, publication year, study design, outcome measure, exposure measure, and whether the analysis was adjusted for covariates. The outcome measure RR refers to relative risk or risk ratio, OR refers to odds ratio, and HR refers to hazard ratio. Two separate meta-analyses are conducted to generate combined dose-response relationships for the bladder and lung cancer studies.
Bladder cancer studies description |
|||||
Study (publication Yr) |
Type of study |
Study population |
Outcome measure |
Exposure measure |
Analysis adjusted for covariates? |
Bates et al.6 |
Case-control |
117 cases and 266 controls were considered. |
OR |
Two arsenic exposure indices (total cumulative exposure) and intake concentration were used as exposure measures. |
Statistical analysis was adjusted for smoking. |
Bates et al.7 |
Case-control |
A total of 114 case control pairs were considered. |
OR |
Exposure to arsenic was estimated from water samples collected from subjects’ current residence. |
Statistical analysis was adjusted for covariates. |
Chen et al.8 |
Case-control |
49 patients with newly diagnosed bladder cancer 224 controls. |
OR |
Average exposure estimated from village they lived in 30 years before and the average AR in well water in that village in 1974 and 1976. |
Statistical analysis was adjusted for smoking and other covariates |
Chen et al.9 |
Prospective (Cohort) study |
A cohort of 8086 subjects |
RR |
Water samples from wells, collected from households. |
Adjusted for smoking and other relevant covariates. |
Chiou et al.10 |
Prospective (Cohort) study |
A cohort of 8102 subjects was considered. |
RR |
Well water samples were assayed to estimate arsenic concentrations to which study subjects were exposed. |
Multivariate analysis was adjusted for smoking and other covariates. |
Karagas et al.11 |
Case-control |
459 bladder cancer cases and 665 controls were considered. |
OR |
Exposure to arsenic was determined by analyzing toenail clipping samples using instrumental neuron activation analysis. |
Adjusted for smoking and other relevant covariates. |
Kurttio et al.12 |
Case -cohort |
61 bladder cancer cases, 49 kidney cancer cases and 275 subjects in the reference cohort were considered. |
RR |
Arsenic exposure was estimated for short and long latency periods and daily dose of arsenic was calculated from reported consumption of drinking water from wells. |
Statistical analysis was adjusted for smoking and other covariates. |
Kwong et al.13 |
Case-control |
832 cases of bladder cancer diagnosed from a population based case control study |
HR |
Both toenail arsenic concentration and concentration from the drinking water were collected. |
Adjusted for smoking and other relevant covariates. |
Meliker et al.14 |
Case-control |
411 bladder cancer cases and 566 controls were considered. |
OR |
A life time exposure to arsenic was predicted using geostatistical modeling. |
Statistical analysis was adjusted for smoking and other relevant covariates. |
Michaud et al.15 |
Case-control |
331 bladder cancer cases and same number of controls were considered. |
OR |
Individual exposure to arsenic was determined using toenail concentrations that served as a biomarker of arsenic concentration. |
Adjusted for smoking and other relevant covariates |
Steinmaus et al.16 |
Case-control |
181 bladder cancer cases and 328 controls were considered. |
OR |
The highest single year cumulative arsenic concentrations to which the subjects were exposed were estimated. |
Statistical analysis was adjusted for smoking and duration of exposure to arsenic. |
Steinmaus et al.17 |
Case-control |
232 bladder and 306 lung cancer cases and 640 controls were considered. |
OR |
Arsenic exposure was based on water quality measurements for the individual’s location. |
Statistical analysis was adjusted for smoking and duration of exposure to arsenic. |
Table 1 Summary of twelve bladder cancer studies selected for meta-analysis
Lung cancer studies description |
|||||
Study (publication Yr) |
Type of study |
Study population |
Outcome measure |
Exposure measure |
Analysis adjusted for covariates? |
Chen et al.18 |
Follow-up study |
A total of 2503 residents and 8088 residents in two arseniasis - endemic areas in Taiwan |
RR |
Arsenic exposure was estimated as lifetime cumulative exposure |
Statistical analysis was adjusted for smoking and other covariates. |
Chen et al.19 |
Follow-up study |
8086 subjects were followed for 11 years, out of which 6888 were included in the final analysis. |
RR |
Arsenic concentration was estimated using water samples collected from the wells used by the subjects. |
Statistical analysis was adjusted for smoking and other covariates. |
Dauphinne et al.20 |
Case-control |
196 lung cancer cases 359 controls |
OR |
Arsenic concentrations from records for community- supplied drinking water and for private wells. |
Statistical analysis was adjusted for smoking and other covariates. |
Garcia et al.21 |
Follow-up study |
3,932 American Indians who participated in the Strong Heart Study from 1989 to 1991 and were followed through 2008. |
HR |
Arsenic exposure measured as the sum of inorganic and methylated species in urine |
Statistical analysis was adjusted for smoking and other covariates. |
Ferreccio et al.22 |
Case-control |
152 lung cancer subjects and 419 controls |
OR |
Water quality records of municipal water companies |
Statistical analysis was adjusted for smoking and other covariates. |
Heck et al.23 |
Case-control |
A total 223 lung cancer cases and 238 controls were considered. |
OR |
Arsenic exposure measures were estimated from to enail concentrations.concentrations. |
Relationship of smoking in addition to arsenic ingestion was investigated. |
Mostafa et al.24 |
Case-referent |
3223 cases and 1588 unmatched case-referents |
OR |
Arsenic exposure estimated by average concentrations for 64 districts. |
Relationship of smoking in addition to arsenic ingestion was investigated. |
Steinmaus et al.17 |
Case-control |
232 bladder and 306 lung cancer cases and 640 controls were considered. |
OR |
Arsenic exposure was based on water quality measurements for the individual’s location. |
Statistical analysis was adjusted for smoking and duration of exposure to arsenic. |
Table 2 Summary of eight lung cancer studies selected for meta-analysis
Ingestion of arsenic through drinking water was considered as the exposure route for both bladder and lung cancer outcomes. The studies included in the meta-analysis reported exposure levels in various ranges and metrics. To address the multiple exposure metrics reported by some studies such as cumulative exposure, average exposure, and highest known exposure, the exposure measure in each study, including toenail concentration, is converted to micro-gram per liter µg/l, which is the most homogeneous metric across the studies.
We consider low to moderate exposure levels as 0-300 µg/l for both bladder cancer and lung cancer studies. In some studies either lower, upper, or both limits are left open. For an open-ended lower limit, we assume that the lower limit is zero. The exposure midpoint is calculated by taking the average of the lower and upper limits of each range except for an open-ended upper limit. For an open-ended upper limit the midpoint is calculated as 1.2 times the lower bound of the open-ended upper limit. The reference midpoint is subtracted from these midpoints and the difference is considered as the doses in subsequent regression models.
A meta-analysis for combining exposure-response relationships from observational studies is in general a difficult problem because a common exposure-response relationship assumption across studies is not realistic. Although the studies are systematically selected to ensure uniformity, the assumption of homogeneity seldom holds for observational studies in environmental epidemiology, public health, or other related fields. Even the studies selected under pre-set criteria are likely to have numerous differences including study populations, exposure metrics, and outcome measures. Since ‘fixed-effects’ models, assume homogeneity across studies, these are not suitable for combining exposure-response relationships from observational studies. ‘Random-effects’ models are more appropriate for combining exposure-response relationships when the exposure-response relationships are similar even though the shape and magnitude vary across studies.
Methods for summarizing observational exposure-response studies quantitatively are well established in the literature.28,29 A simple exposure-response model to estimate the trend effect assumes that the adjusted odds ratios are uncorrelated. Since the calculation of the adjusted odds ratios are based on the same reference category, this assumption is violated and the trend estimate becomes inefficient. An approximated variance-covariance matrix is estimated from the fitted table of exposure-response relationship.29 The approximated variance-covariance matrix is then used in the weighted least square estimation of the trend parameter. Trend parameter estimates obtained this improved method are both consistent and efficient.
The efficient estimation of the trend effect in an exposure-response relationship also depends on the model under consideration. A simple linear exposure-response model is limited since the exposure-response relation is overly simplified. Also, the exposure-response relationship across many studies addressing the same question may have differential nonlinear shapes. Linear exposure-response models are not able to quantify the true relationship between exposure and responses in these nonlinear cases. Thus to encompass a wide range of exposure-response relationships, flexible models, such as fractional polynomials (FP) and spline regression (SR), are preferable to linear models as they provide a large group of flexible models to incorporate various shapes of exposure-response relations.5 FP models are a family of models defined by covariate power transformations of a continuous exposure variable. The values of the power are selected from a small number of predefined integers and non-integers.30 A conventional linear model is a special case of FP models. SR models can come very close to the nonparametric regression models as the splines belong to a family of smooth functions.
A combined trend estimate of the exposure-response relationship is obtained by first estimating a study-specific functional form. At study-specific analysis, flexible FP models and SR models are used to estimate such a relationship. The study specific estimates obtained from the first-stage FP models or SR models are then combined through multi-variate meta-analysis. FP and SR models provide a rich class of regression models for exposure-response relationship in epidemiology. However, implementation of these models is not as widespread as linear exposure-response models in epidemiology and other related fields. Bagnardi et al.5 implemented FP and SR models for combining exposure-response results from alcohol consumption and all-cause mortality studies. In following sections, we discuss the methodology for combining exposure-response relationships across observational studies using FP and SR models.
Combining exposure-response relationships using fractional polynomials
The log relative risk for study is modeled using first and second order FPs at study-specific analysis. Relative risk is a generic term that represents the risk ratio for cumulative incidence data in prospective cohort studies, and the odds ratio for case-control data in retrospective studies. The first and second order FP models for study i are presented as follows:
(1)
(2)
Here m = 12 for bladder cancer studies, m = 8 for lung cancer studies, and the powers p, p1, and p2 take values from a pre-specified vector c = (−2, −1, −0.5, 0, 0.5, 1, 2, 3) as considered by Bagnardi et al.5 Such a power specification contains considerable flexibility to encompass a wide variety of exposure-response shapes. With the pre-specified index set p for power transformation, one can fit eight first-order models and thirty-six second-order models with all possible combinations of exponents for p1 and p2. The best fit model is selected as the one that provides highest likelihood for the data under that model. Other criteria for model selection are the deviance and the Akaike Information Criterion (AIC). For both of these criteria smaller values indicate better fit to the data. Both deviance and AIC are considered in selecting the best first-order and the best second-order fractional polynomial models.
The best fit models are then applied to estimate the exposure-response relationship for each study included in the analysis. In order to efficiently estimate trends in dose-response relationships for each study, the correlation among the log relative risks is taken into account. Estimated trends in dose-response relationship from each study are then combined according to principles of multivariate random effects meta-analysis to obtain a pooled functional relation.31 The R package Dosresmeta32 was used to implement the fractional polynomial models to both bladder and lung cancer studies.
Combining exposure-response relationships using spline regression models
Spline regression (SR) models for fitting exposure-response relationships are smoothly joined piecewise polynomials of order q. The joint point is known as ‘spline knot’. It is crucial to select the spline knot positions properly. Usually knot positions are selected based on how well the spline model with selected knots fits the data. The shape of exposure-response relationship plays an important role in knot selection process as well. A B-spline regression model with degree 2 and four knot positions usually at the quantiles of the exposure level x has 7 degrees of freedom. The shape of the exposure-response relationship may be used to select the number of knots effectively. The B-spline regression model for log relative risk for the ith study can be written as,
Where the truncated power basis function is defined as
For degree = 3, the cubic spline regression model becomes,
Where the truncated power basis function is defined as
Although SR models are promising in fitting study-specific flexible exposure-response relationships, all 12 bladder cancer and 8 lung cancer studies are extremely sparse with only three to five data points. With only one knot position at 50th percentile, we were able to estimate the regression parameters but not their variance-covariance matrix. Thus it was not possible to combine the study specific regression coefficients from the study specific spline models. As a result, we do not include study specific spline models in the multivariate meta-analysis for the bladder cancer studies or lung cancer studies. This means that only estimates of the coefficients from the fractional polynomial models are combined using the multivariate meta-analysis.
Multivariate meta-analysis to combine results from FP and SR models
To conduct multivariate meta-analysis, we obtain -dimensional vector of regression coefficient estimates and associated estimated variance-covariance matrices A random effect multivariate meta-analysis Gasparrini [31] can be written as follows:
Where . The model in equation (3) is obtained from two independent within-study and between-study components. In the within study component, a dimensional multivariate normal distribution centered at a vector of true unknown outcome parameters for study i. In the between study component, , where represents the unknown between study variance-covariance matrix. The unknown parameter vector represents the population average parameters of the average exposure response relationship. Estimation of the parameter vector and unknown variance-covariance matrix completes the multivariate meta-analysis with a random-effects model. The R package Dosresmeta32 is used to carry out the multivariate meta-analysis using first and second order fractional polynomial models for both the bladder and lung cancer studies. The combined exposure-response models are then used to predict the risk for bladder and lung cancer in low to moderate exposure ranges of (0-100) µg/l and (0-300) µg/l.
From the twelve bladder cancer studies and the eight lung cancer studies, we separately fit the dose-response data to eight first-order and thirty-six second-order fractional polynomial models. As discussed in section 3.1, the number of first order models and the number of second order models follow from the choice of powers for the FP models.
To select the best models from each group, several goodness of fit statistics, including deviance and Akaike Information Criterion (AIC) are calculated. Specifically, Figure 3 presents the AIC values for both first and second-order fractional polynomial models for the data from the bladder cancer studies. Among these eight first-order fractional models, Figure 3 shows that the model where , has the lowest AIC. We refer to this model as Model 1. Among the second-order fractional polynomials models, Figure 3 shows that the models that have the lowest AIC are , where and , which we refer to as Model 2, and , where , which we refer to as Model 3. We estimate the combined relative risks from Model 1, Model 2, and Model 3.
For lung cancer studies, we implement the same set of first and second-order models as these appear to be the best fitted models. According to the goodness of fit statistics, deviance and AIC, the best fitted models for the lung cancer studies are Model 1, Model 2 and Model 3, which are the same as the bladder cancer studies. Estimated study-specific coefficients from these fractional polynomial models for the bladder cancer studies are combined using multivariate meta-analysis. Combined predicted relative risks at dose levels 0 to 100 µg/l and 0 to 300 µg/l from Model 1, Model 2, and Model 3 are presented in Figure 4 and Figure 5. Similarly, for lung cancer studies, Figure 6 and Figure 7 present combined predicted relative risks at dose levels 0 to 100 µg/l and 0 to 300 µg/l respectively.
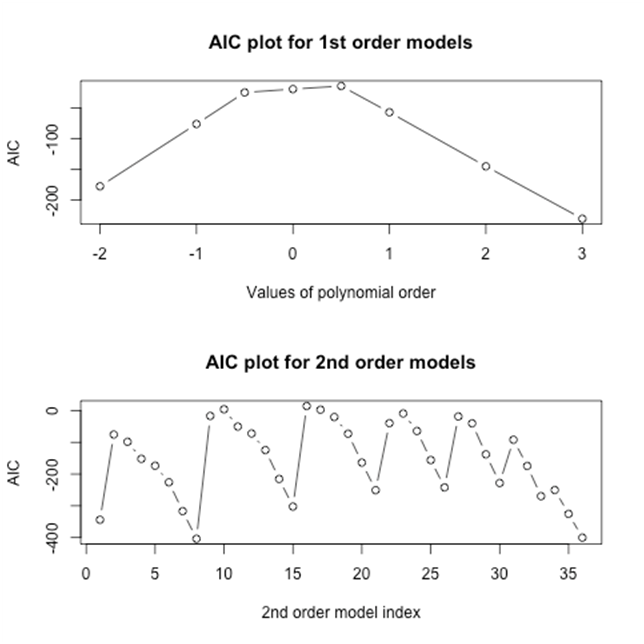
Figure 3 Goodness of fit statistics (AIC) for FP models for bladder cancer studies. Top: AIC plots for first-order fractional polynomial models with p=-2,-1,-.5,0,.5,1,2,3; Bottom: AIC plots for second-order fractional polynomial models with p1=p2=-2,-1,-.5,0,.5,1,2,3.
Bladder cancer
As discussed in Section 3.3, the regression coefficients of Model 1, Model 2 and Model 3 are combined through multivariate meta-analysis methods. The combined estimated coefficients are used to estimate the relative risks for doses from 0 to 100 µg/l and to compute the corresponding 95% confidence intervals. These results are shown in Figure 4.
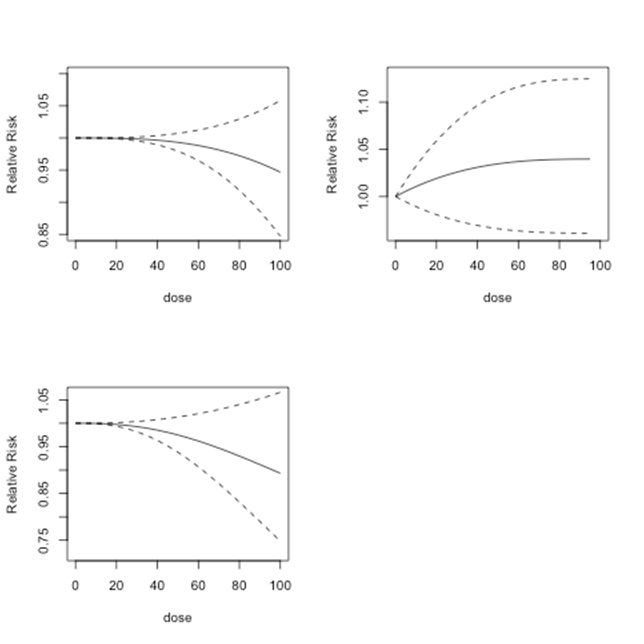
Figure 4 Bladder cancer studies: predicted relative risk relative risk for doses from 0 to 100 µg/l and 95% confidence intervals. Top Left: First-order fitted fractional polynomial model with p = 3 (Model 1); Top Right: Second-order fitted fractional polynomial model with p1 = -2, p2 = 3 (Model 2); Bottom Left:
Second-order fitted fractional polynomial model with p1=p2=3 (Model 3).
In each figure, the solid black line shows the predicted relative risk and the dashed lines show the corresponding 95% confidence intervals. The top left graph shows the results from Model 1, the top right graph shows the results from Model 2, and the bottom left graph shows the results from Model 3. For doses between 0 and 100µg/l, Model 1 predicts relative risk close to 1 or lower. This implies that at dose levels between 0 and 100µg/l, there is no or minimal risk of bladder cancer. Model 2 produces relative risk estimates that have a slight upward trend. However, since these relative risk estimates never exceed 1.05, the results indicate no or minimal risk of bladder cancer at doses between 0 and 100µg/l. Model 3 finds similar low or no risk of bladder cancer for dose levels between 0 and 100µg/l. For each model, as shown by the confidence interval, the predicted relative risk estimates become less reliable when the dose levels increase.
In Figure 5, we plot relative risk estimates from Model 1, Model 2 and Model 3 for doses between 0 and 300 µg/l. Relative risk estimates from Model 1 show no risk up to dose level 150 µg/l and may even slightly reduce the risk of bladder cancer. Model 2 shows lower risk at low-dose levels and slightly higher risk at dose levels 150 µg/l or more. Model 3 predicts relatively higher relative risk at dose level 250 µg/l and higher. However, none of these results are statistically significant. In addition, at higher dose levels each model predicts less reliable relative risk estimates.

Figure 5 Lung cancer studies: predicted relative risk for doses from 0 to 100µg/l. Top Left: First-order fitted fractional polynomial model with p = 3 (Model 1); Top Right: Second-order fitted fractional polynomial model with p1 = -2, p2 = 3 (Model 2); Bottom Left: Second-order fitted fractional polynomial model with p1=p2=3 (Model 3).
Lung cancer
The combined predicted relative risks for lung cancer studies are presented in Figure 6 and Figure 7. Since the combined predicted relative risks from Model 1 and Model 2 are close to one, these models find no evidence of lung cancer risks at doses 0 to 100µg/l (Figure 6). The combined predicted relative risks from Model 3 show an upward trend, which implies some evidence of risk beginning at approximately 40µg/l. However, the relative risk only increases to 1.1, which implies a relatively minor risk.
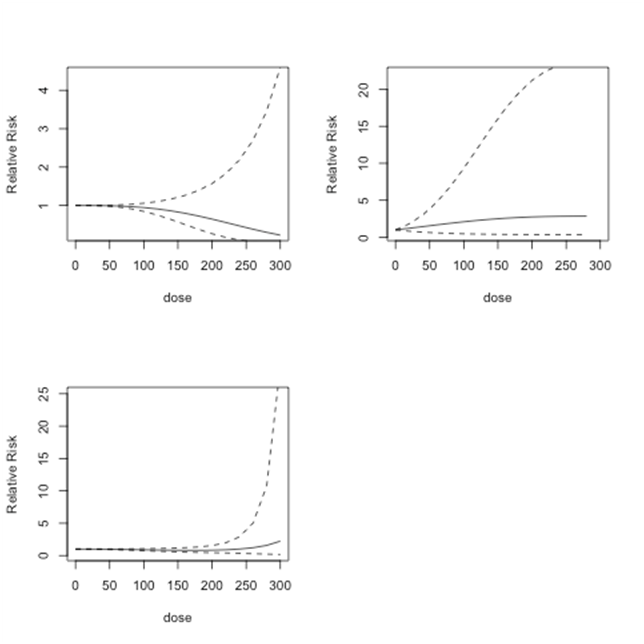
Figure 6 Bladder cancer studies: predicted relative risk for doses from 0 to 300 µg/l and 95% confidence intervals. Top Left: First-order fitted fractional polynomial model with p = 3 (Model 1); Top Right: Second-order fitted fractional polynomial model with p1 = -2, p2 = 3 (Model 2); Bottom Left: Second-order fitted fractional polynomial model with p1=p2=3 (Model 3).
Figure 7 shows the predicted dose-response models for dose levels 0 to 300 µg/l for the same three models as in Figure 6. Below 150µg/l, Model 1 shows no indication of risk of lung cancer. After 150 µg/l, there is an increase in predicted relative risk. However, the results in all of the models are not statistically significant. Model 2 indicates no risk up to 300 µg/l. Model 3 shows an increasing risk after dose level 100 µg/l, which declines approximately after 230µg/l.
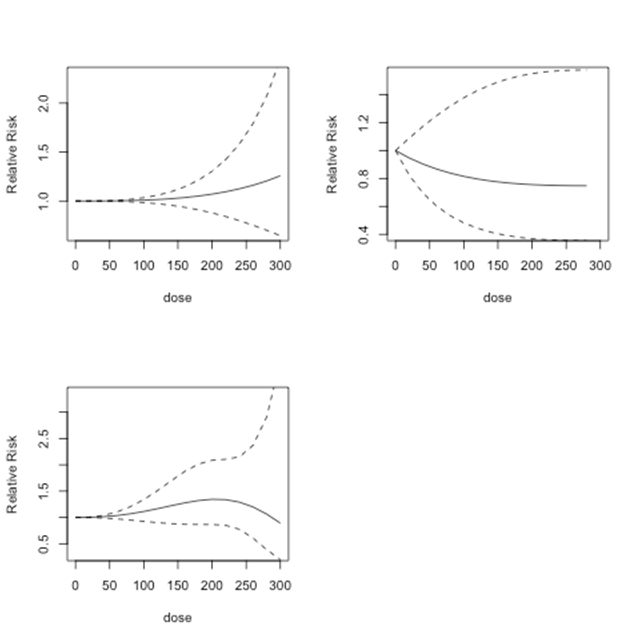
Figure 7 Lung cancer studies: predicted relative risk for doses from 0 to 300 µg/l. Top Left: First-order fitted fractional polynomial model with p = 3 (Model 1); Top Right: Second-order fitted fractional polynomial model with p1 = -2, p2 = 3 (Model 2); Bottom Left: Second-order fitted fractional polynomial model with p1=p2=3 (Model 3).
This article applies fractional polynomial and spline regression models to determine the shapes of the dose-response relationships between bladder and lung cancer risk and exposure to low to moderate dose arsenic. Our results are similar to Mink et al.3 who found a generally weak and statistically insignificant relationship between low-dose exposure to arsenic and bladder cancer and Begum et al.4 who found a generally weak relationship between bladder and lung cancer and exposure to low-dose arsenic. We estimate overall risks of bladder and lung cancers by combining findings from systematically selected studies on these cancers under both linear and non-linear modeling assumptions. We consider fractional polynomial models that include a linear model as a special case, and the spline regression models. Fractional polynomial models do not provide any statistically significant relative risks of bladder and lung cancer at low to moderate dose levels of arsenic exposure. These models predict no or minimal risk for bladder and lung cancer at low to moderate dose levels (0 to 150) µg/l. It is also to be noted that at higher dose levels each model predicts less reliable relative risk estimates for bladder and lung cancer. Overall, we found a weak and statistically insignificant relationship between both bladder and lung cancer and low to moderate exposure to arsenic.
However, it is important to observe that both bladder and lung cancer studies have only few data points in the range of exposure – response set (Figure 8 and Figure 9). Since sample size affects the statistical significance, we note that further investigation with larger number of points in the range of exposure – response set is required to draw firm conclusions.
Spline regression models are promising in fitting study-specific flexible exposure-response relationships. However, as shown in Figure 8 and Figure 9 there are only 3 to 5 data points in each of the bladder cancer and lung cancer studies. Figure 8 and Figure 9 present study specific exposure response relationships for bladder and lung cancer studies respectively. As evident from Figure 8 and Figure 9, there is lack of homogeneity in terms of exposure metrics as well as shape of the exposure response relationships. These figures also show the sparseness in the data for which the computation of the study specific spline models was not possible. With only one knot position at 50th percentile, we were able to estimate the regression parameters but not their variance-covariance matrix. Thus it was not possible to combine the study specific regression coefficients from the study specific spline models. As a result, we do not include study specific spline models in the multivariate meta-analysis for the bladder cancer studies or lung cancer studies. This means that only estimates of the coefficients from the fractional polynomial models are combined using the multivariate meta-analysis.
Future studies investigating the association between exposure to low to moderate levels of arsenic and internal cancers can extend this work by including additional co-variate information. For instance, smoking status could be included to determine its effect on the dose-response relationships. This article can also be extended by obtaining additional data on low and especially moderate dose arsenic exposure levels and internal cancer for finer analyses. Due to the computational limitations for spline regression models with sparse data, our results were limited to only fractional polynomial models. This could be overcome, with additional data or the development of methods for modeling sparse data.

© . This is an open access article distributed under the terms of the, which permits unrestricted use, distribution, and build upon your work non-commercially.
2 7