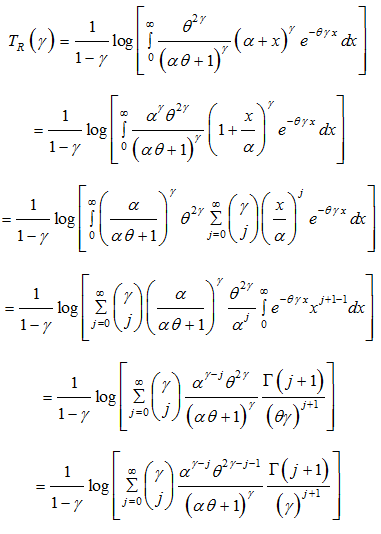eISSN: 2378-315X

Biometrics & Biostatistics International Journal

Correspondence:

Received: January 01, 1970 | Published: ,

Citation: DOI:

Download PDF

Abstract

In this paper some of the important mathematical properties including moment generating function, mean deviations, order statistics, Bonferroni and Lorenz curves, Renyi entropy and stress strength reliability of two-parameter Lindley distribution (TPLD) of Shanker & Mishra¹ have been discussed. Its goodness of fit over exponential and Lindley distributions have been illustrated with some real lifetime data-sets and found that TPLD is preferable over exponential and Lindley distributions for modeling lifetime data-sets.

Keywords: mean deviations; order statistics, bonferroni and lorenz curves, entropy, stress-strength reliability, goodness of fit

Introduction

The probability density function (p.d.f.) and the cumulative distribution function (c.d.f.) of distribution, introduced in the context of Bayesian analysis as a counter example of fiducial statistics, are given by

f (x; θ) = \frac{θ^{2}}{θ + 1} (1 + x) e^{- θ x}; x > 0, θ > 0

$f (x; θ) = \frac{θ^{2}}{θ + 1} (1 + x) e^{- θ x}; x > 0, θ > 0$ (1.1)

F (x; θ) = 1 - [1 + \frac{θ x}{θ + 1}] e^{- θ x}; x > 0, θ > 0

$F (x; θ) = 1 - [1 + \frac{θ x}{θ + 1}] e^{- θ x}; x > 0, θ > 0$ (1.2)

The detailed study about its mathematical properties, estimation of parameter and application showing the superiority of Lindley distribution over exponential distribution for the waiting times before service of the bank customers has been done by Ghitany et al.² The Lindley distribution has been generalized extended and modified by different researchers including^1,3-19 are some among others.

The probability density function (p.d.f.) and cumulative distribution function (c.d.f) of two-parameter Lindley distribution (TPLD) of Shanker & Mishra¹ are given by

f (x; α, θ) = \frac{θ^{2}}{α θ + 1} (α + x) e^{- θ x}; x > 0, θ > 0, α θ > - 1

$f (x; α, θ) = \frac{θ^{2}}{α θ + 1} (α + x) e^{- θ x}; x > 0, θ > 0, α θ > - 1$ (1.3)

F (x; α, θ) = 1 - [\frac{1 + α θ + θ x}{α θ + 1}] e^{- θ x}; x > 0, θ > 0, α θ > - 1

$F (x; α, θ) = 1 - [\frac{1 + α θ + θ x}{α θ + 1}] e^{- θ x}; x > 0, θ > 0, α θ > - 1$ (1.4)

At $α = 1$ $α = 1$ , both (1.3) and (1.4) reduce to the corresponding expressions (1.1) and (1.2) of Lindley distribution. The first two moments about origin and the variance of TPLD of Shanker & Mishra¹ are given by

$μ_{1}^{'} = \frac{α θ + 2}{θ (α θ + 1)}$ $μ_{1}^{'} = \frac{α θ + 2}{θ (α θ + 1)}$ (1.5)

μ_{2}^{'} = \frac{2 (α θ + 3)}{θ^{2} (α θ + 1)}

$μ_{2}^{'} = \frac{2 (α θ + 3)}{θ^{2} (α θ + 1)}$ (1.6)

μ_{2} = \frac{α^{2} θ^{2} + 4 α θ + 2}{θ^{2} {(α θ + 1)}^{2}}

$μ_{2} = \frac{α^{2} θ^{2} + 4 α θ + 2}{θ^{2} {(α θ + 1)}^{2}}$ (1.7)

At $α = 1$ $α = 1$ , these moments reduce to the corresponding moments of Lindley distribution. Shanker & Mishra¹ have derived and discussed some of its mathematical properties such as shape, moments, coefficient of variation, coefficient of skewness and kurtosis, hazard rate function, mean residual life function and stochastic orderings. They have also discussed the estimation of its parameters using maximum likelihood estimation and method of moments and its goodness of fit over Lindley distribution. It has been observed that many important mathematical properties of this distribution have not been studied.

In the present paper some of the important mathematical properties including moment generating function, mean deviations, order statistics, Bonferroni and Lorenz curves, Renyi entropy and stress strength reliability of TPLD of Shanker & Mishra¹ have been derived and discussed. Its goodness of fit over exponential and Lindley distributions have been illustrated with some real lifetime data-sets and found that TPLD gives better fit than exponential and Lindley distributions.

Moment generating function

The moment generating function, $(M_{X} (t))$ $(M_{X} (t))$ of TPLD (1.3) can be obtained as

M_{X} (t) = \frac{θ^{2}}{α θ + 1} \infty \int 0 e^{- (θ - t)} (α + x) d x

$M_{X} (t) = \frac{θ^{2}}{α θ + 1} \int_{0}^{\infty} e^{- (θ - t)} (α + x) d x$

= \frac{θ^{2}}{α θ + 1} [\frac{α}{θ - t} + \frac{1}{{(θ - t)}^{2}}]

$= \frac{θ^{2}}{α θ + 1} [\frac{α}{θ - t} + \frac{1}{{(θ - t)}^{2}}]$

= \frac{θ^{2}}{α θ + 1} [\frac{α}{θ} \infty \sum k = 0 {(\frac{t}{θ})}^{k} + \frac{1}{θ^{2}} \infty \sum k = 0 (\begin{matrix} k + 1 k \end{matrix}) {(\frac{t}{θ})}^{k}]

$= \frac{θ^{2}}{α θ + 1} [\frac{α}{θ} \sum_{k = 0}^{\infty} {(\frac{t}{θ})}^{k} + \frac{1}{θ^{2}} \sum_{k = 0}^{\infty} (\begin{matrix} k + 1 \\ k \end{matrix}) {(\frac{t}{θ})}^{k}]$

= \infty \sum k = 0 (\frac{α θ + 1 + k}{α θ + 1}) {(\frac{t}{θ})}^{k}

$= \sum_{k = 0}^{\infty} (\frac{α θ + 1 + k}{α θ + 1}) {(\frac{t}{θ})}^{k}$

It can be easily seen that the expression for $μ_{r}^{'}$ $μ_{r}^{'}$ obtained as the coefficient of $\frac{t^{r}}{r!}$ $\frac{t^{r}}{r!}$ is given as

μ_{r}^{'} = \frac{r! (α θ + r + 1)}{θ^{r} (α θ + 1)}; r = 1, 2, 3, ...

$μ_{r}^{'} = \frac{r! (α θ + r + 1)}{θ^{r} (α θ + 1)}; r = 1, 2, 3, ...$

For $α = 1$ $α = 1$ , $μ_{r}^{'}$ $μ_{r}^{'}$ reduces to the corresponding $μ_{r}^{'}$ $μ_{r}^{'}$ of Lindley distribution.

Mean deviations

The amount of scatter in a population is measured to some extent by the totality of deviations usually from mean and median. These are known as the mean deviation about the mean and the mean deviation about the median defined by $δ_{1} (X) = \infty \int 0 | x - μ | f (x) d x$ $δ_{1} (X) = \int_{0}^{\infty} | x - μ | f (x) d x$ and $δ_{2} (X) = \infty \int 0 | x - M | f (x) d x$ $δ_{2} (X) = \int_{0}^{\infty} | x - M | f (x) d x$ , respectively, where $μ = E (X)$ $μ = E (X)$ and $M = Median (X)$ $M = Median (X)$ . The measures $δ_{1} (X)$ $δ_{1} (X)$ and $δ_{2} (X)$ $δ_{2} (X)$ can be calculated using the relationships

δ_{1} (X) = μ \int 0 (μ - x) f (x) d x + \infty \int μ (x - μ) f (x) d x

$δ_{1} (X) = \int_{0}^{μ} (μ - x) f (x) d x + \int_{μ}^{\infty} (x - μ) f (x) d x$

= μ F (μ) - μ \int 0 x f (x) d x - μ [1 - F (μ)] + \infty \int μ x f (x) d x

$= μ F (μ) - \int_{0}^{μ} x f (x) d x - μ [1 - F (μ)] + \int_{μ}^{\infty} x f (x) d x$

= 2 μ F (μ) - 2 μ + 2 \infty \int μ x f (x) d x

$= 2 μ F (μ) - 2 μ + 2 \int_{μ}^{\infty} x f (x) d x$

= 2 μ F (μ) - 2 μ \int 0 x f (x) d x

$= 2 μ F (μ) - 2 \int_{0}^{μ} x f (x) d x$ (3.1)

and

δ_{2} (X) = M \int 0 (M - x) f (x) d x + \infty \int M (x - M) f (x) d x

$δ_{2} (X) = \int_{0}^{M} (M - x) f (x) d x + \int_{M}^{\infty} (x - M) f (x) d x$

= M F (M) - M \int 0 x f (x) d x - M [1 - F (M)] + \infty \int M x f (x) d x

$= M F (M) - \int_{0}^{M} x f (x) d x - M [1 - F (M)] + \int_{M}^{\infty} x f (x) d x$

= - μ + 2 \infty \int M x f (x) d x

$= - μ + 2 \int_{M}^{\infty} x f (x) d x$

= μ - 2 M \int 0 x f (x) d x

$= μ - 2 \int_{0}^{M} x f (x) d x$ (3.2)

Using p.d.f. (1.3), and expression for mean of two-parameter Lindley distribution, we have

$μ \int 0 x f (x) d x = μ - \frac{{θ^{2} (μ^{2} + α μ) + 2 θ μ + (α θ + 2)} e^{- θ μ}}{θ (α θ + 1)}$ $\int_{0}^{μ} x f (x) d x = μ - \frac{{θ^{2} (μ^{2} + α μ) + 2 θ μ + (α θ + 2)} e^{- θ μ}}{θ (α θ + 1)}$ (3.3)

Using expressions from (3.1), (3.2) and (3.3), and little algebraic simplification, the mean deviation about mean, $δ_{1} (X)$ $δ_{1} (X)$ and the mean deviation about median, $δ_{2} (X)$ $δ_{2} (X)$ of TPLD (1.3) are obtained as

$δ_{1} (X) = \frac{2 (θ μ + α θ + 2) e^{- θ μ}}{θ (α θ + 1)}$ $δ_{1} (X) = \frac{2 (θ μ + α θ + 2) e^{- θ μ}}{θ (α θ + 1)}$ (3.4)

and $δ_{2} (X) = \frac{2 {θ^{2} (M^{2} + α M) + 2 θ M + (α θ + 2)} e^{- θ M}}{θ (α θ + 1)} - μ$ $δ_{2} (X) = \frac{2 {θ^{2} (M^{2} + α M) + 2 θ M + (α θ + 2)} e^{- θ M}}{θ (α θ + 1)} - μ$ (3.5)

It can be easily seen that expressions (3.4) and (3.5) of TPLD (1.3) reduce to the corresponding expressions of Lindley distribution at $α = 1$ $α = 1$ .

Order statistics

Let $X_{1}, X_{2}, ..., X_{n}$ $X_{1}, X_{2}, ..., X_{n}$ be a random sample of size from two-parameter Lindley distribution (1.3). Let $X_{(1)} < X_{(2)} < ... < X_{(n)}$ $X_{(1)} < X_{(2)} < ... < X_{(n)}$ denote the corresponding order statistics. The p.d.f. and the c.d.f. of the $k$ $k$ th order statistic, say $Y = X_{(k)}$ $Y = X_{(k)}$ are given by

f_{Y} (y) = \frac{n!}{(k - 1)! (n - k)!} F^{k - 1} (y) {1 - F (y)}^{n - k} f (y)

$f_{Y} (y) = \frac{n!}{(k - 1)! (n - k)!} F^{k - 1} (y) {1 - F (y)}^{n - k} f (y)$

= \frac{n!}{(k - 1)! (n - k)!} n - k \sum l = 0 (\begin{matrix} n - k l \end{matrix}) {(- 1)}^{l} F^{k + l - 1} (y) f (y)

$= \frac{n!}{(k - 1)! (n - k)!} \sum_{l = 0}^{n - k} (\begin{matrix} n - k \\ l \end{matrix}) {(- 1)}^{l} F^{k + l - 1} (y) f (y)$

and

$F_{Y} (y) = n \sum j = k (\begin{matrix} n j \end{matrix}) F^{j} (y) {1 - F (y)}^{n - j}$ $F_{Y} (y) = \sum_{j = k}^{n} (\begin{matrix} n \\ j \end{matrix}) F^{j} (y) {1 - F (y)}^{n - j}$

$= n \sum j = k n - j \sum l = 0 (\begin{matrix} n j \end{matrix}) (\begin{matrix} n - j l \end{matrix}) {(- 1)}^{l} F^{j + l} (y)$ $= \sum_{j = k}^{n} \sum_{l = 0}^{n - j} (\begin{matrix} n \\ j \end{matrix}) (\begin{matrix} n - j \\ l \end{matrix}) {(- 1)}^{l} F^{j + l} (y)$

respectively, for $k = 1, 2, 3, ..., n$ $k = 1, 2, 3, ..., n$

Thus, the p.d.f. and the c.d.f of the th order statistics of TPLD (1.3) are obtained as

$f_{Y} (y) = \frac{n! θ^{2} (α + x) e^{- θ x}}{(α θ + 1) (k - 1)! (n - k)!} n - k \sum l = 0 (\begin{matrix} n - k l \end{matrix}) {(- 1)}^{l} \times {[1 - \frac{1 + α θ + θ x}{α θ + 1} e^{- θ x}]}^{k + l - 1}$ $f_{Y} (y) = \frac{n! θ^{2} (α + x) e^{- θ x}}{(α θ + 1) (k - 1)! (n - k)!} \sum_{l = 0}^{n - k} (\begin{matrix} n - k \\ l \end{matrix}) {(- 1)}^{l} \times {[1 - \frac{1 + α θ + θ x}{α θ + 1} e^{- θ x}]}^{k + l - 1}$

and

$F_{Y} (y) = n \sum j = k n - j \sum l = 0 (\begin{matrix} n j \end{matrix}) (\begin{matrix} n - j l \end{matrix}) {(- 1)}^{l} {[1 - \frac{1 + α θ + θ x}{α θ + 1} e^{- θ x}]}^{j + l}$ $F_{Y} (y) = \sum_{j = k}^{n} \sum_{l = 0}^{n - j} (\begin{matrix} n \\ j \end{matrix}) (\begin{matrix} n - j \\ l \end{matrix}) {(- 1)}^{l} {[1 - \frac{1 + α θ + θ x}{α θ + 1} e^{- θ x}]}^{j + l}$

It can be easily verified that the expressions for the p.d.f. and c.d.f. of the th order statistics of TPLD (1.3) reduce to the expressions for the p.d.f. and c.d.f. of the th order statistics of Lindley distribution at $α = 1$ $α = 1$

Bonferroni and lorenz curves

The Bonferroni and Lorenz curves²⁰ and Bonferroni and Gini indices have applications not only in economics to study income and poverty, but also in other fields like reliability, demography, insurance and medicine. The Bonferroni and Lorenz curves are defined as

$B (p) = \frac{1}{p μ} q \int 0 x f (x) d x = \frac{1}{p μ} ⎡ ⎢ ⎣ \infty \int 0 x f (x) d x - \infty \int q x f (x) d x ⎤ ⎥ ⎦ = \frac{1}{p μ} ⎡ ⎢ ⎣ μ - \infty \int q x f (x) d x ⎤ ⎥ ⎦$ $B (p) = \frac{1}{p μ} \int_{0}^{q} x f (x) d x = \frac{1}{p μ} [\int_{0}^{\infty} x f (x) d x - \int_{q}^{\infty} x f (x) d x] = \frac{1}{p μ} [μ - \int_{q}^{\infty} x f (x) d x]$ (5.1)

$L (p) = \frac{1}{μ} q \int 0 x f (x) d x = \frac{1}{μ} ⎡ ⎢ ⎣ \infty \int 0 x f (x) d x - \infty \int q x f (x) d x ⎤ ⎥ ⎦ = \frac{1}{μ} ⎡ ⎢ ⎣ μ - \infty \int q x f (x) d x ⎤ ⎥ ⎦$ $L (p) = \frac{1}{μ} \int_{0}^{q} x f (x) d x = \frac{1}{μ} [\int_{0}^{\infty} x f (x) d x - \int_{q}^{\infty} x f (x) d x] = \frac{1}{μ} [μ - \int_{q}^{\infty} x f (x) d x]$ (5.2)

respectively or equivalently

$B (p) = \frac{1}{p μ} p \int 0 F^{- 1} (x) d x$ $B (p) = \frac{1}{p μ} \int_{0}^{p} F^{- 1} (x) d x$ (5.3)

and $L (p) = \frac{1}{μ} p \int 0 F^{- 1} (x) d x$ $L (p) = \frac{1}{μ} \int_{0}^{p} F^{- 1} (x) d x$ (5.4)

respectively, where $μ = E (X)$ $μ = E (X)$ and $q = F^{- 1} (p)$ $q = F^{- 1} (p)$ .

The Bonferroni and Gini indices are thus defined as

$B = 1 - 1 \int 0 B (p) d p$ $B = 1 - \int_{0}^{1} B (p) d p$ (5.5)

and $G = 1 - 2 1 \int 0 L (p) d p$ $G = 1 - 2 \int_{0}^{1} L (p) d p$ (5.6)

respectively.

Using p.d.f. (1.3), we get

$\infty \int q x f (x) d x = \frac{{θ^{2} (q^{2} + α q) + 2 θ q + (α θ + 2)} e^{- θ q}}{θ (α θ + 1)}$ $\int_{q}^{\infty} x f (x) d x = \frac{{θ^{2} (q^{2} + α q) + 2 θ q + (α θ + 2)} e^{- θ q}}{θ (α θ + 1)}$ (5.7)

Now using equation (5.7) in (5.1) and (5.2), we get

$B (p) = \frac{1}{p} [1 - \frac{{θ^{2} (q^{2} + α q) + 2 θ q + (α θ + 2)} e^{- θ q}}{α θ + 2}]$ $B (p) = \frac{1}{p} [1 - \frac{{θ^{2} (q^{2} + α q) + 2 θ q + (α θ + 2)} e^{- θ q}}{α θ + 2}]$ (5.8)

and $L (p) = 1 - \frac{{θ^{2} (q^{2} + α q) + 2 θ q + (α θ + 2)} e^{- θ q}}{α θ + 2}$ $L (p) = 1 - \frac{{θ^{2} (q^{2} + α q) + 2 θ q + (α θ + 2)} e^{- θ q}}{α θ + 2}$ (5.9)

Now using equations (5.8) and (5.9) in (5.5) and (5.6), the Bonferroni and Gini indices of TPLD (1.3) are obtained as

$B = 1 - \frac{{θ^{2} (q^{2} + α q) + 2 θ q + (α θ + 2)} e^{- θ q}}{α θ + 2}$ $B = 1 - \frac{{θ^{2} (q^{2} + α q) + 2 θ q + (α θ + 2)} e^{- θ q}}{α θ + 2}$ (5.10)

$G = - 1 + \frac{2 {θ^{2} (q^{2} + α q) + 2 θ q + (α θ + 2)} e^{- θ q}}{α θ + 2}$ $G = - 1 + \frac{2 {θ^{2} (q^{2} + α q) + 2 θ q + (α θ + 2)} e^{- θ q}}{α θ + 2}$ (5.11)

The Bonferroni and Gini indices of Lindley distribution are particular cases of the Bonferroni and Gini indices (5.10) and (5.11) of TPLD (1.3) for $α = 1$ $α = 1$ .

Renyi entropy

An entropy of a random variable is a measure of variation of uncertainty. A popular entropy measure is Renyi entropy.²¹ If is a continuous random variable having probability density function $f (.)$ $f (.)$ , then Renyi entropy is defined as

$T_{R} (γ) = \frac{1}{1 - γ} log {\int f^{γ} (x) d x}$ $T_{R} (γ) = \frac{1}{1 - γ} \log {\int f^{γ} (x) d x}$

where $γ > 0 and γ \neq 1$ $γ > 0 and γ \neq 1$ .

Thus, the Renyi entropy for TPLD (1.3) can be obtained as

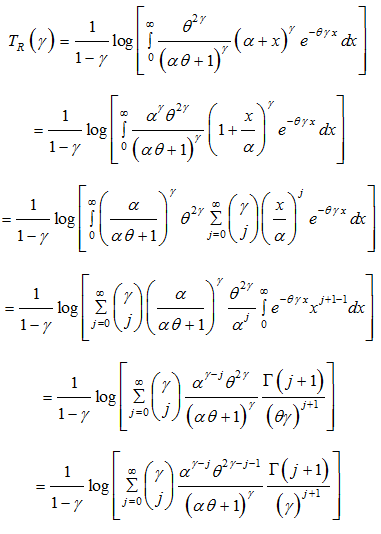
The Renyi entropy of Lindley distribution is a particular case of the Renyi entropy TPLD at $α = 1$ $α = 1$ .

Stress-strength reliability

The stress- strength reliability describes the life of a component which has random strength that is subjected to a random stress . When the stress applied to it exceeds the strength, the component fails instantly and the component will function satisfactorily till $X > Y$ $X > Y$ . Therefore, $R = P (Y < X)$ $R = P (Y < X)$ is a measure of component reliability and in statistical literature it is known as stress-strength parameter. It has wide applications in almost all areas of knowledge especially in engineering such as structures, deterioration of rocket motors, static fatigue of ceramic components, aging of concrete pressure vessels etc.

Let $X$ $X$ and $Y$ $Y$ be independent strength and stress random variables having TPLD (1.3) with parameter $(α_{1}, θ_{1})$ $(α_{1}, θ_{1})$ and $(α_{2}, θ_{2})$ $(α_{2}, θ_{2})$ respectively. Then the stress-strength reliability $R$ $R$ is obtained as

$R = P (Y < X) = \infty \int 0 P (Y < X | X = x) f_{X} (x) d x$ $R = P (Y < X) = \int_{0}^{\infty} P (Y < X | X = x) f_{X} (x) d x$

$= \infty \int 0 f (x; α_{1}, θ_{1}) F (x; α_{2}, θ_{2}) d x$ $= \int_{0}^{\infty} f (x; α_{1}, θ_{1}) F (x; α_{2}, θ_{2}) d x$

$= 1 - \frac{θ_{1}^{2} [2 θ_{2} + (α_{1} θ_{2} + α_{2} θ_{2} + 1) (θ_{1} + θ_{2}) + α_{1} (α_{2} θ_{2} + 1) {(θ_{1} + θ_{2})}^{2}]}{(α_{1} θ_{1} + 1) (α_{2} θ_{2} + 1) {(θ_{1} + θ_{2})}^{2}}$ $= 1 - \frac{θ_{1}^{2} [2 θ_{2} + (α_{1} θ_{2} + α_{2} θ_{2} + 1) (θ_{1} + θ_{2}) + α_{1} (α_{2} θ_{2} + 1) {(θ_{1} + θ_{2})}^{2}]}{(α_{1} θ_{1} + 1) (α_{2} θ_{2} + 1) {(θ_{1} + θ_{2})}^{2}}$

The expression of stress-strength reliability of Lindley distribution is a particular case of the expression of stress-strength reliability of TPLD (1.3) at $α_{1} = α_{2} = 1$ $α_{1} = α_{2} = 1$ .

Estimation of parameters

Method of moment estimate of parameters

The TPLD (1.3) has two parameters to be estimated and so the first two moments about origin are required to estimate parameters. Using the first two moments about origin, we have

$\frac{μ_{2}^{'}}{{(μ_{1}^{'})}^{2}} = k (Say) = \frac{2 (α θ + 3) (α θ + 1)}{{(α θ + 2)}^{2}}$ $\frac{μ_{2}^{'}}{{(μ_{1}^{'})}^{2}} = k (Say) = \frac{2 (α θ + 3) (α θ + 1)}{{(α θ + 2)}^{2}}$ (8.1.1)

Taking $b = α θ$ $b = α θ$ , we get

$\frac{μ_{2}^{'}}{{(μ_{1}^{'})}^{2}} = \frac{2 (b + 3) (b + 1)}{{(b + 2)}^{2}} = \frac{2 b^{2} + 8 b + 6}{b^{2} + 4 b + 4} = k$ $\frac{μ_{2}^{'}}{{(μ_{1}^{'})}^{2}} = \frac{2 (b + 3) (b + 1)}{{(b + 2)}^{2}} = \frac{2 b^{2} + 8 b + 6}{b^{2} + 4 b + 4} = k$

This gives a quadratic equation in $b$ $b$ as

$(2 - k) b^{2} + 4 (2 - k) b + 2 (3 - 2 k) = 0$ $(2 - k) b^{2} + 4 (2 - k) b + 2 (3 - 2 k) = 0$ (8.1.2)

Replacing the first and second moments about origin $μ_{1}^{'}$ $μ_{1}^{'}$ and $μ_{2}^{'}$ $μ_{2}^{'}$ by their respective sample moments, an estimate of $k$ $k$ can be obtained and substituting the value of $k$ $k$ in equation (8.1.2), an estimate of can be obtained. Substituting this estimate of in the expression for the mean of TPLD (1.3), moment estimate $˜ θ$ $\tilde{θ}$ of $θ$ $θ$ can be obtained as

$˜ θ = (\frac{b + 2}{b + 1}) \frac{1}{¯ x}$ $\tilde{θ} = (\frac{b + 2}{b + 1}) \frac{1}{\bar{x}}$ (8.1.3)

Finally, moment estimate $˜ α$ $\tilde{α}$ of $α$ $α$ can be obtained as

$˜ θ = (\frac{b + 2}{b + 1}) \frac{1}{¯ x}$ $\tilde{θ} = (\frac{b + 2}{b + 1}) \frac{1}{\bar{x}}$ (8.1.3)

Finally, moment estimate $˜ α$ $\tilde{α}$ of $α$ $α$ can be obtained as

$˜ α = \frac{b}{˜ θ}$ $\tilde{α} = \frac{b}{\tilde{θ}}$

b. Maximum likelihood estimate of parameters

Let $(x_{1}, x_{2}, x_{3}, ..., x_{n})$ $(x_{1}, x_{2}, x_{3}, ..., x_{n})$ be a random sample from TPLD (1.3). Let $f_{x}$ $f_{x}$ be the observed frequency in the sample corresponding to $X = x (x = 1, 2, 3, ... k)$ $X = x (x = 1, 2, 3, ... k)$ such that $k \sum x = 1 f_{x} = n$ $\sum_{x = 1}^{k} f_{x} = n$ , where $k$ $k$ is the largest observed value having non-zero frequency. The likelihood function, $L$ $L$ of TPLD (1.3) is given by

$L = {(\frac{θ^{2}}{α θ + 1})}^{n} n \prod i = 1 {(α + x)}_{x}^{f_{x}} e^{- n θ ¯ x}$ $L = {(\frac{θ^{2}}{α θ + 1})}^{n} \prod_{i = 1}^{n} {(α + x)}^{f_{x}} e^{- n θ \bar{x}}$ (8.2.1)

The log likelihood function is thus obtained as

$log L = n log θ^{2} - n log (α θ + 1) + k \sum x = 1 f_{x} log (α + x) - n θ ¯ x$ $\log L = n \log θ^{2} - n \log (α θ + 1) + \sum_{x = 1}^{k} f_{x} \log (α + x) - n θ \bar{x}$ (8.2.2)

where $¯ x$ $\bar{x}$ is the sample mean.

The two log likelihood equations are obtained as

$\frac{\partial log L}{\partial θ} = \frac{2 n}{θ} - \frac{n α}{α θ + 1} - n ¯ x = 0$ $\frac{\partial \log L}{\partial θ} = \frac{2 n}{θ} - \frac{n α}{α θ + 1} - n \bar{x} = 0$

$\frac{\partial log L}{\partial α} = - \frac{n θ}{α θ + 1} + k \sum x = 1 \frac{f_{x}}{α + x} = 0$ $\frac{\partial \log L}{\partial α} = - \frac{n θ}{α θ + 1} + \sum_{x = 1}^{k} \frac{f_{x}}{α + x} = 0$

It can be easily seen that equation (8.2.3) gives $¯ x = \frac{α θ + 2}{θ (α θ + 1)} = μ_{1}^{'}$ $\bar{x} = \frac{α θ + 2}{θ (α θ + 1)} = μ_{1}^{'}$ , mean of TPLD. The equations (8.2.3) and (8.2.4) do not seem to be solved directly. However, Fisher’s scoring method can be applied to solve these equations iteratively. We have

$\frac{\partial^{2} log L}{\partial θ^{2}} = - \frac{2 n}{θ^{2}} + \frac{n α^{2}}{{(α θ + 1)}^{2}}$ $\frac{\partial^{2} \log L}{\partial θ^{2}} = - \frac{2 n}{θ^{2}} + \frac{n α^{2}}{{(α θ + 1)}^{2}}$

$\frac{\partial^{2} log L}{\partial θ \partial α} = - \frac{n}{{(α θ + 1)}^{2}}$ $\frac{\partial^{2} \log L}{\partial θ \partial α} = - \frac{n}{{(α θ + 1)}^{2}}$ (8.2.6)

$\frac{\partial^{2} log L}{\partial α^{2}} = \frac{n θ^{2}}{{(α θ + 1)}^{2}} - k \sum x = 1 \frac{f_{x}}{{(α + x)}^{2}}$ $\frac{\partial^{2} \log L}{\partial α^{2}} = \frac{n θ^{2}}{{(α θ + 1)}^{2}} - \sum_{x = 1}^{k} \frac{f_{x}}{{(α + x)}^{2}}$ (8.2.7)

The maximum likelihood estimates of parameters are the solution of the following equations

${⎡ ⎢ ⎣ \begin{matrix} \frac{\partial^{2} log L}{\partial θ^{2}} & \frac{\partial^{2} log L}{\partial θ \partial α} \frac{\partial^{2} log L}{\partial θ \partial α} & \frac{\partial^{2} log L}{\partial α^{2}} \end{matrix} ⎤ ⎥ ⎦}_{\begin{matrix} ˆ θ = θ_{0} ˆ α = α_{0} \end{matrix}} [\begin{matrix} ˆ θ = θ_{0} ˆ α = α_{0} \end{matrix}] = {⎡ ⎣ \begin{matrix} \frac{\partial log L}{\partial θ} \frac{\partial log L}{\partial α} \end{matrix} ⎤ ⎦}_{\begin{matrix} ˆ θ = θ_{0} ˆ α = α_{0} \end{matrix}}$ ${[\begin{matrix} \frac{\partial^{2} \log L}{\partial θ^{2}} & \frac{\partial^{2} \log L}{\partial θ \partial α} \\ \frac{\partial^{2} \log L}{\partial θ \partial α} & \frac{\partial^{2} \log L}{\partial α^{2}} \end{matrix}]}_{\begin{matrix} \hat{θ} = θ_{0} \\ \hat{α} = α_{0} \end{matrix}} [\begin{matrix} \hat{θ} = θ_{0} \\ \hat{α} = α_{0} \end{matrix}] = {[\begin{matrix} \frac{\partial \log L}{\partial θ} \\ \frac{\partial \log L}{\partial α} \end{matrix}]}_{\begin{matrix} \hat{θ} = θ_{0} \\ \hat{α} = α_{0} \end{matrix}}$

where $θ_{0} and α_{0}$ $θ_{0} and α_{0}$ are initial values of $θ and α$ $θ and α$ as given by the method of moments. These equations are solved iteratively till sufficiently close estimates of $ˆ θ and ˆ α$ $\hat{θ} and \hat{α}$ are obtained.

Applications of two-parameter Lindley distribution

The two-parameter Lindley distribution (TPLD) has been fitted to a number of lifetime data- sets. In this section, we present the fitting of two-parameter Lindley distribution to five real lifetime data-sets and compare its goodness of fit with the one parameter exponential and Lindley distributions data sets (1-5).

1.1	1.4	1.3	1.7	1.9	1.8	1.6	2.2	1.7	2.7	4.1	1.8
1.5	1.2	1.4	3	1.7	2.3	1.6	2

Data set 1: This data set represents the lifetime’s data relating to relief times (in minutes) of 20 patients receiving an analgesic and reported by Gross et al.²²

18.83	20.8	21.657	23.03	23.23	24.05	24.321	25.5	25.52	25.8	26.69	26.77
26.78	27.05	27.67	29.9	31.11	33.2	33.73	33.76	33.89	34.76	35.75	35.91
36.98	37.08	37.09	39.58	44.045	45.29	45.381

Data set 2: This data set is the strength data of glass of the aircraft window reported by Fuller et al.²³

0.8	0.8	1.3	1.5	1.8	1.9	1.9	2.1	2.6	2.7	2.9	3.1
3.2	3.3	3.5	3.6	4	4.1	4.2	4.2	4.3	4.3	4.4	4.4
4.6	4.7	4.7	4.8	4.9	4.9	5	5.3	5.5	5.7	5.7	6.1
6.2	6.2	6.2	6.3	6.7	6.9	7.1	7.1	7.1	7.1	7.4	7.6
7.7	8	8.2	8.6	8.6	8.6	8.8	8.8	8.9	8.9	9.5	9.6
9.7	9.8	10.7	10.9	11	11	11.1	11.2	11.2	11.5	11.9	12.4
12.5	12.9	13	13.1	13.3	13.6	13.7	13.9	14.1	15.4	15.4	17.3
17.3	18.1	18.2	18.4	18.9	19	19.9	20.6	21.3	21.4	21.9	23
27	31.6	33.1	38.5

Data set 3: This data set represents the waiting times (in minutes) before service of 100 Bank customers and examined and analyzed by Ghitany et al.² for fitting the Lindley²⁴ distribution.

0.55	0.93	1.25	1.36	1.49	1.52	1.58	1.61	1.64	1.68	1.73	1.81
2	0.74	1.04	1.27	1.39	1.49	1.53	1.59	1.61	1.66	1.68	1.76
1.82	2.01	0.77	1.11	1.28	1.42	1.5	1.54	1.6	1.62	1.66	1.69
1.76	1.84	2.24	0.81	1.13	1.29	1.48	1.5	1.55	1.61	1.62	1.66
1.7	1.77	1.84	0.84	1.24	1.3	1.48	1.51	1.55	1.61	1.63	1.67
1.7	1.78	1.89

Data set 4: The data set represents the strength of 1.5cm glass fibers measured at the National Physical Laboratory, England. Unfortunately, the units of measurements are not given in the paper, and they are taken from Smith & Naylor²⁵

17.88	28.92	33	41.52	42.12	45.6	48.8	51.84	51.96	54.12	55.56	67.8
68.44	68.64	68.88	84.12	93.12	98.64	105.12	105.84	127.92	128.04	173.4

Data set 5: The data set is from Lawless.²⁶ The data given arose in tests on endurance of deep groove ball bearings. The data are the number of million revolutions before failure for each of the 23 ball bearings in the life tests and they are:

In order to compare distributions, $- 2 ln L$ $- 2 \ln L$ , AIC (Akaike Information Criterion), AICC (Akaike Information Criterion Corrected), BIC (Bayesian Information Criterion), K-S Statistics (Kolmogorov-Smirnov Statistics) for five real data - sets have been computed (Table 1). The formulae for computing AIC, AICC, BIC, and K-S Statistics are as follows:

	Model	Estimate of Parameters		— 2ln L	AIC	AICC	BIC	K-S Statistics
	Model	$ˆ θ$ $\hat{θ}$	$ˆ α$ $\hat{α}$	— 2ln L	AIC	AICC	BIC	K-S Statistics
Data 1	Lindley	0.816118		60.50	62.50	62.72	63.49	0.341
	Exponential TPLD	0.526316 1.545110	— 0.31285	65.67 40.71	67.67 44.71	67.90 45.41	68.67 46.70	0.389 0.204
Data 2	Lindley	0.062988		253.99	255.99	256.13	257.42	0.333
	Exponential TPLD	0.032455 0.103985	— 5.25330	274.53 231.82	276.53 235.82	276.67 236.25	277.96 238.69	0.426 0.298
Data 3	Lindley	0.186571		638.07	640.07	640.12	642.68	0.058
	Exponential TPLD	0.101245 0.196210	0.337078	658.04 635.75	660.04 639.75	660.08 639.87	662.65 639.75	0.163 0.040
Data 4	Lindley	0.996116		162.56	164.56	164.62	166.70	0.371
	Exponential TPLD	0.663647 2.146474	0.257373	177.66 91.56	179.66 95.56	179.73 95.63	181.80 97.36	0.402 0.361
Data 5	Lindley	0.027321		231.47	233.47	233.66	234.61	0.149
	Exponential TPLD	0.013845 0.035434	10.12355	242.87 223.52	244.87 227.52	245.06 228.12	246.01 229.79	0.263 0.098

Table 1 MLE’s, — 2ln L, AIC, AICC, BIC, K-S Statistics of the fitted distributions of data sets 1-5

$A I C = - 2 ln L + 2 k$ $A I C = - 2 \ln L + 2 k$ ,

$A I C C = A I C + \frac{2 k (k + 1)}{(n - k - 1)}$ $A I C C = A I C + \frac{2 k (k + 1)}{(n - k - 1)}$ ,

$B I C = - 2 ln L + k ln n$ $B I C = - 2 \ln L + k \ln n$ and

$D = Sup x | F_{n} (x) - F_{0} (x) |$ $D = \underset{x}{Sup} | F_{n} (x) - F_{0} (x) |$ , where $k$ $k$ = the number of parameters, $n$ $n$ = the sample size and $F_{n} (x)$ $F_{n} (x)$ is the empirical distribution function.

The best distribution corresponds to lower $- 2 ln L$ $- 2 \ln L$ , AIC, AICC, BIC, and K-S statistics.

Conclusion

In the present paper some of the important mathematical properties including moment generating function, mean deviations, order statistics, Bonferroni and Lorenz curves, entropy and stress strength reliability of two-parameter Lindley distribution (TPLD) of Shanker & Mishra¹ have been derived and discussed. The distribution has been fitted to some real lifetime data-sets to test its goodness of fit over exponential and Lindley distributions. It is obvious from the fitting of TPLD that it gives better fitting than exponential and Lindley distributions and hence TPLD is preferable over exponential and Lindley distributions for modeling lifetime data-sets from different fields of knowledge.