Abstract
In this paper, a general expression for the
th factorial moment of zero-truncated Poisson-Lindley distribution (ZTPLD) has been obtained and hence the first four moments about origin has been given. A very simple and alternative method for finding moments of ZTPLD has also been suggested. The expression for the moment generating function of ZTPLD has been obtained. Both ZTPD (Zero-truncated Poisson distribution) and ZTPLD have been fitted using maximum likelihood estimate to a number of data- sets from demography, biological sciences and social sciences and it has been observed that in most cases ZTPLD gives much closer fits than ZTPD while in some cases ZTPD gives much closer fits than ZTPLD.
Keywords: poisson-lindley distribution, zero-truncated distribution, moments, estimation of parameter, goodness of fit
Abbreviations
ZTPLD, zero-truncated poisson-lindley distribution; ZTPD, zero-truncated poisson distribution; PLD, poisson-lindley distribution; PMF, probability mass function; PDF, probability density function; SBPD, size-biased poisson distribution; MLE, maximum likelihood estimate; MOME, method of moment estimate; MVUE, minimum variance unbiased estimation; SBPD, size-biased poisson distribution
Introduction
Zero-truncated distributions, in probability theory, are certain discrete distributions having support the set of positive integers. These distributions are applicable for the situations when the data to be modeled originate from a mechanism that generates data excluding zero-counts.
Let
is the original distribution with support non negative positive integers. Then the zero-truncated version of with the support the set of positive integers is given by
(1.1)
The Poisson-Lindley distribution (PLD) with parameter
and having probability mass function (p.m.f.)
(1.2)
has been introduced by Sankaran1 to model count data. Recently, Shanker et al.2 have done an extensive study on its applications to Biological Sciences and found that PLD provides a better fit than Poisson distribution to almost all biological science data. The PSD arises from the Poisson distribution when its parameter
follows Lindley distribution3 with probability density function (p.d.f.).
(1.3)
Detailed study of Lindley distribution (1.3) has been done by Ghitany et al.4 and shown that (1.3) is a better model than exponential distribution. Recently, Shanker et al.2 showed that (1.3) is not always a better model than the exponential distribution for modeling lifetimes data. In fact, Shanker et al.2 has done a very extensive and comparative study on modeling of lifetimes data using exponential and Lindley distributions and discussed various lifetimes examples to show the superiority of Lindley over exponential and that of exponential over Lindley distribution. The PLD has been extensively studied by Sankaran1 and Ghitany & Mutairi5 and they have discussed its various properties. The Lindley distribution and the PLD has been generalized by many researchers. Shanker et al.6 obtained a two parameter Poisson-Lindley distribution by compounding Poisson distribution with a two parameter Lindley distribution introduced by Shanker et al.7 A quasi Poisson-Lindley distribution has been introduced by Shanker et al.8 by compounding Poisson distribution with a quasi Lindley distribution introduced by Shanker et al.9 Shanker et al.10 obtained a discrete two parameter Poisson-Lindley distribution by mixing Poisson distribution with a two parameter Lindley distribution for modeling waiting and survival times data introduced by Shanker et al.11 Further, Shanker et al.12 obtained a new quasi Poisson-Lindley distribution by compounding Poisson distribution with a new quasi Lindley distribution introduced by Shanker et al.13,14
In this paper, the nature of zero-truncated Poisson distribution (ZTPD) and zero-truncated Poisson-Lindley distribution (ZTPLD) has been compared and studied using graphs for different values of their parameter. A general expression for the
th factorial moment of ZTPLD has been obtained and the first four moment about origin has been given. A very simple and easy method for finding moments of ZTPLD has been suggested. Both ZTPD and ZTPLD have been fitted to a number of data sets from different fields to study their goodness of fits and superiority of one over the other.
Zero-truncated poisson and poisson-Lindley distribution
Zero-truncated poisson distribution (ZTPD)
Using (1.1) and the p.m.f. of Poisson distribution, the p.m.f. of zero-truncated Poisson distribution (ZTPD) given by
(2.1.1)
was obtained independently by Plackett1 and David et al.16 to model count data that structurally excludes zero counts. An extension of a truncated Poisson distribution and estimation in a truncated Poisson distribution when zeros and some ones are missing has been discussed by Cohen.17,18 Tate et al.19 has discussed minimum variance unbiased estimation (MVUE) for the truncated Poisson distribution.
Zero-truncated poisson-Lindley distribution (ZTPLD)
Using (1.1) and (1.2), the p.m.f. of zero-truncated Poisson- Lindley distribution (ZTPLD) given by
(2.2.1)
was obtained by Ghitany et al.20 to model count data for the missing zeros. It has been shown by Ghitany et al.20 that ZTPLD can also arise from the size-biased Poisson distribution (SBPD) with p.m.f.
(2.2.2)
when its parameter
follows a distribution having p.d.f.
(2.2.3)
Thus the p.m.f. of ZTPLD is obtained as
(2.2.4)
which is the p.m.f. of ZTPLD with parameter
.
To study the nature and behaviors of ZTPD and ZTPLD for different values of its parameter, a number of graphs of their probability densities have been drawn and presented in Figure 1.
Moments and related measures
Moments of ZTPD
The
th factorial moment of the ZTPD (2.1.1) can be obtained as
, where
(3.1.1)
Substituting
in (3.1.1), the first four factorial moments can be obtained and, therefore, using the relationship between factorial moments and moments about origin, the first four moments about origin of ZTPD (2.1.1) are obtained as
Generating Function: The probability generating function of the ZTPD (2.1.1) is obtained as
The moment generating function of the ZTPD (2.1.1) is thus given by
Moments of ZTPLD
The
th factorial moment of the ZTPLD (2.2.1) can be obtained as
, where
Using (2.2.4), we get
Taking
in place of
, we get
It is obvious that the expression within the bracket is
and hence, we have
Using gamma integral and little algebraic simplification, we get finally, a general expression for the
th factorial moment of the ZTPLD (2.2.1) as
(3.2.1)
Substituting
in (3.2.1), the first four factorial moment can be obtained and then using the relationship between factorial moments and moments about origin, the first four moments about origin of the ZTPLD (2.2.1) are given by
Generating function: The probability generating function of the ZTPLD (2.2.1) is obtained as
The moment generating function of the ZTPLD (2.2.1) is thus given by
A Simple method of finding moments of ZTPLD
Using (2.2.4), the
th moment about origin of ZTPLD (2.2.1) can be obtained as
(4.1)
It is obvious that the expression under the bracket in (4.1) is the
th moment about origin of the SBPD. Taking
in (4.1) and using the first moment about origin of the SBPD, the first moment about origin of the ZTPLD (2.2.1) is obtained as
(4.2)
Again taking
in (4.1) and using the second moment about origin of the SBPD, the second moment about origin of the ZTPLD (2.2.1) is obtained as
(4.3)
Similarly, taking
in (4.1) and using the respective moments of SBPD, we get finally, after a little simplification, the third and the fourth moments about origin of the ZTPLD (2.2.1) as
(4.4)
(4.5)
Estimation of parameter
Estimation of parameter of ZTPD
Maximum likelihood estimate (MLE): Let
be a random sample of size
from the ZTPD (2.1.1). The MLE
of
of ZTPD (2.1.1) is given by the solution of the following non linear equation.
, where
is the sample mean
Method of moment estimate (MOME): Let
be a random sample of size
from the ZTPD (2.1.1). Equating the first population moment about origin to the corresponding sample moment, the MOME
of
of ZTPD (2.1.1) is the solution of the following non linear equation.
, where
is the sample mean
Thus both MLE and MOME give the same estimate of the parameter
of ZTPD (2.1.1).
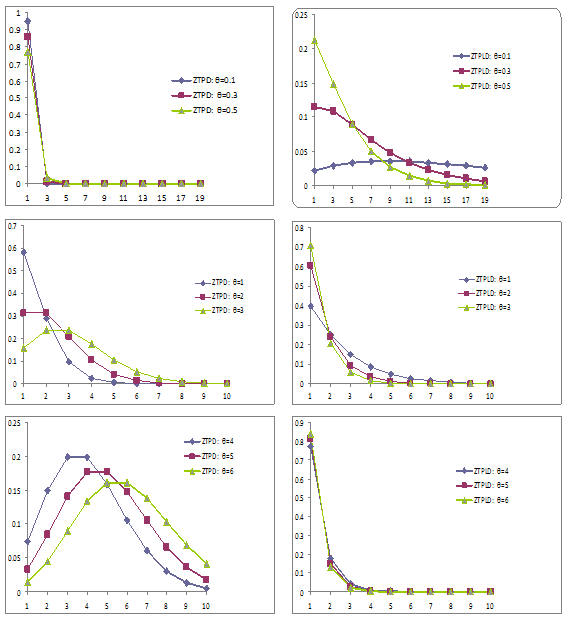
Figure 1 Graph of probability functions of ZTPD and ZTPLD for different values of their parameter. The left hand side graphs are for ZTPD and right hand side graphs are for ZTPLD.
Estimation of parameter of ZTPLD
Maximum likelihood estimate (MLE): Let
be a random sample of size
from the ZTPLD (2.2.1) and let
be the Observed frequency in the sample corresponding to
such that
, where
is the largest observed value having non-zero frequency. The likelihood function
of the ZTPLD (2.2.1) is given by
(5.1.1)
The log likelihood function is given by
and the log likelihood equation is thus obtained as
The maximum likelihood estimate
of
is the solution of the equation
and is given by the solution of the following non-linear equation
(5.1.2)
where
is the sample mean. This non-linear equation can be solved by any numerical iteration methods such as Newton- Raphson method, Bisection method, Regula –Falsi method etc. Ghitany et al.20 showed that the MLE
of
is consistent and asymptotically normal.
Method of moment estimate (MOME): Let
be a random sample of size
from the ZTPLD (2.2.1). Equating the first population moment about origin to the corresponding sample moment, the MOME
of
of ZTPLD (2.2.1) is the solution of the following cubic equation.
, where
is the sample mean. Ghitany et al.20 showed that the MOME
of
is consistent and asymptotically normal.
Applications
In this section, both ZTPD and ZTPLD have been fitted to a number of data-sets using maximum likelihood estimates relating to demography, biological sciences, and social sciences to test their goodness of fits and it has been observed that in most of the cases ZTPLD gives much closer fits than ZTPD and in some cases ZTPD gives much closer fits than ZTPLD.
Mortality
Mortality does not depend only on biological factors; it depends upon the prevailing health conditions, medical facilities, the socio-economic and cultural factors. In developing and under-developed countries, the mortality among infants and children is found much higher than that among youngsters. The high infant mortality has thrown a serious challenge to the medical personnel and is considered as one of the sensitive position of existing medical and health facilities in the population.
Number of neonatal deaths |
Observed number of mothers |
Expected frequency |
ZTPD |
ZTPLD |
1 |
409 |
399.7 |
408.1 |
2 |
88 |
102.3 |
89.4 |
3
4
5 |
19
5
1 |
|
19.3
|
Total |
522 |
522.0 |
522.0 |
ML Estimate |
|
|
|
|
|
3.464 |
0.145 |
d.f. |
|
1 |
2 |
P-value |
|
0.0627 |
0.9301 |
Table 1 The number of mothers of the rural area having at least one live birth and one neonatal death.
Number of neonatal deaths |
Observed number of mothers |
Expected frequency |
ZTPD |
ZTPLD |
1 |
71 |
66.5 |
72.3 |
2 |
32 |
35.1 |
28.4 |
3
4
5 |
7
5
3 |
|
10.9
|
Total |
118 |
118.0 |
118.0 |
ML Estimate |
|
|
|
|
|
0.696 |
2.274 |
d.f. |
|
1 |
2 |
P-value |
|
0.4041 |
0.3208 |
Table 2 The number of mothers of the estate area having at least one live birth and one neonatal death.
Number of infant and child deaths |
Observed number of mothers |
Expected frequency |
ZTPD |
ZTPLD |
1 |
176 |
164.3 |
171.6 |
2 |
44 |
61.2 |
51.3 |
3
4
5 |
16
6
2 |
|
15.0
|
Total |
244 |
244.0 |
244.0 |
ML Estimate |
|
|
|
|
|
7.301 |
1.882 |
d.f. |
|
1 |
2 |
P-value |
|
0.0069 |
0.3902 |
Table 3 The number of mothers of the urban area with at least two live births by the number of infant and child deaths.
Number of infant and child deaths |
Observed number of mothers |
Expected frequency |
ZTPD |
ZTPLD |
1 |
745 |
708.9 |
738.1 |
2 |
212 |
255.1 |
214.8 |
3 |
50 |
61.2 |
61.3 |
4
5
6 |
21
7
3 |
|
17.2
|
Total |
1038 |
1038.0 |
1038.0 |
ML Estimate |
|
|
|
|
|
37.046 |
4.773 |
d.f. |
|
2 |
3 |
P-value |
|
0.0 |
0.1892 |
Table 4 The number of mothers of the rural area with at least two live births by the number of infant and child deaths.
Number of infant deaths |
Observed number of mothers |
Expected frequency |
ZTPD |
ZTPLD |
1 |
683 |
659.0 |
674.4 |
2 |
145 |
177.4 |
154.1 |
3
4
5 |
29
11
5 |
|
34.6
|
Total |
873 |
873.0 |
873.0 |
ML Estimate |
|
|
|
|
|
8.718 |
5.310 |
d.f. |
|
1 |
2 |
P-value |
|
0.0031 |
0.0703 |
Table 5 The number of literate mothers with at least one live birth by the number of infant deaths.
Number of child deaths |
Observed number of mothers |
Expected frequency |
ZTPD |
ZTPLD |
1 |
89 |
76.8 |
83.4 |
2 |
25 |
39.9 |
32.3 |
3
4
5
6 |
11
6
3
1 |
|
12.2
|
Total |
135 |
135.0 |
135.0 |
ML Estimate |
|
|
|
|
|
7.90 |
3.428 |
d.f. |
|
1 |
2 |
P-value |
|
0.0049 |
0.1801 |
Table 6 The number of mothers of the completed fertility having experienced at least one child death.
Number of neonatal deaths |
Observed number of mothers |
Expected frequency |
ZTPD |
ZTPLD |
1 |
567 |
545.8 |
561.4 |
2 |
135 |
162.5 |
139.7 |
3 |
28 |
32.3 |
34.2 |
4
5 |
11
5 |
|
|
Total |
746 |
746.0 |
746.0 |
ML Estimate |
|
|
|
|
|
26.855 |
3.839 |
d.f. |
|
2 |
2 |
P-value |
|
0.0 |
0.1467 |
Table 7 The number of mothers having at least one neonatal death.
In this section, an attempt has been made to test the suitability of ZTPD and ZTPLD in describing the neonatal deaths as well as of infant and child deaths experienced by mothers. The data-sets considered here are the data of Sri Lanka and India. The data-sets of Meegama et al.21 have been used as the data of Sri Lanka whereas the data from the survey conducted by Lal22 and the survey of Kadam Kuan, Patna, conducted in 1975 and referred to by Mishra23 have been used as the data of India. It is obvious from the fittings of ZTPD and the ZTPLD that ZTPLD gives much closer fits in almost all cases except in Table 2. Hence, in case of demographic data, ZTPLD is a better alternative than ZTPD to model count data.
Biological sciences
In this section, an attempt has been made to test the goodness of fit of both ZTPD and ZTPLD on many data- sets relating to biological sciences. It has been observed that ZTPLD gives much closer fits than ZTPD in almost all cases except in Table 11 regarding the distribution of the number of leaf spot grade of Ichinose variety of Mulberry. Thus in biological sciences ZTPLD is a better model than ZTPD to model zero-truncated count data.
Number of european red mites
|
Observed frequency |
Expected frequency |
ZTPD |
ZTPLD |
1 |
38 |
28.7 |
36.1 |
2 |
17 |
25.7 |
20.5 |
3 |
10 |
15.3 |
11.2 |
4
5
6
7
8 |
9
3
2
1
0 |
|
5.9
|
Total |
80 |
80.0 |
80.0 |
ML Estimate |
|
|
|
|
|
9.827 |
2.467 |
d.f. |
|
2 |
3 |
P-value |
|
0.0073 |
0.4813 |
Table 8 Number of european red mites
on apple leaves, reported by Garman.24
Number of yeast cells counts per Mm square |
Observed frequency |
Expected frequency |
ZTPD |
ZTPLD |
1 |
128 |
121.3 |
127.6 |
2 |
37 |
49.2 |
40.9 |
3
4
5
6 |
18
3
1
0 |
|
|
Total |
187 |
187.0 |
187.0 |
ML Estimate |
|
|
|
|
|
5.228 |
1.034 |
d.f. |
|
1 |
1 |
P-value |
|
0.0222 |
0.3092 |
Table 9 Number of yeast cell counts observed per mm square, reported by Student.25
Number of fly eggs |
Observed frequency |
Expected frequency |
ZTPD |
ZTPLD |
1 |
22 |
15.3 |
26.8 |
2 |
18 |
21.9 |
19.8 |
3 |
18 |
20.8 |
13.9 |
4 |
11 |
14.9 |
9.5 |
5 |
9 |
8.5 |
6.4 |
6
7
8
9 |
6
3
0
1 |
|
|
Total |
88 |
88.0 |
88.0 |
ML Estimate |
|
|
|
|
|
6.677 |
3.743 |
d.f. |
|
4 |
4 |
P-value |
|
0.1540 |
0.4419 |
Table 10 The number of counts of flower heads as per the number of fly eggs reported by Finney & Varley.26
Number of leaf spot grade |
Observed frequency |
Expected frequency |
ZTPD |
ZTPLD |
1 |
18 |
14.2 |
23.0 |
2 |
15 |
18.7 |
16.3 |
3 |
10 |
16.5 |
11.1 |
4 |
14 |
10.9 |
7.3 |
5 |
13 |
9.7 |
12.4 |
Total |
70 |
70.0 |
70.0 |
ML Estimate |
|
|
|
|
|
6.311 |
7.476 |
d.f. |
|
3 |
3 |
P-value |
|
0.0974 |
0.0582 |
Table 11 The number of leaf spot grade of Ichinose variety of Mulberry, reported by Khurshid.27
Number of leaf spot grade |
Observed frequency |
Expected frequency |
ZTPD |
ZTPLD |
1 |
37 |
28.5 |
36.7 |
2 |
16 |
26.7 |
21.4 |
3 |
15 |
16.7 |
12.0 |
4
5 |
8
8 |
|
6.6
7.3 |
Total |
84 |
84.0 |
84.0 |
ML Estimate |
|
|
|
|
|
8.329 |
2.477 |
d.f. |
|
2 |
3 |
P-value |
|
0.0155 |
0.4795 |
Table 12 The number of leaf spot grade of Kokuso-20 variety of Mulberry, reported by Khurshid.27
Number of sites with particles |
Observed frequency |
Expected frequency |
ZTPD |
ZTPLD |
1 |
122 |
115.9 |
124.8 |
2 |
50 |
57.4 |
46.8 |
3 |
18 |
18.9 |
17.1 |
4
5 |
4
4 |
|
|
Total |
198 |
198.0 |
198.0 |
ML Estimate |
|
|
|
|
|
2.14 |
0.51 |
d.f. |
|
2 |
2 |
P-value |
|
0.3430 |
0.7749 |
Table 13 The number of counts of sites with particles from Immuno gold data, reported by Mathews.28
Number of times hares caught |
Observed frequency |
Expected frequency |
ZTPD |
ZTPLD |
1 |
184 |
176.6 |
182.6 |
2 |
55 |
66.0 |
55.3 |
3
4
5 |
14
4
4 |
|
16.4
|
Total |
261 |
261.0 |
261.0 |
ML Estimate |
|
|
|
|
|
2.45 |
0.61 |
d.f. |
|
1 |
2 |
P-value |
|
0.1175 |
0.7371 |
Table 14 The number of snowshoe hares counts captured over 7 days, reported by Keith & Meslow.29
Social Sciences
In this section, an attempt has been made to test the goodness of fit test of both ZTPD and ZTPLD on many data-sets relating to social sciences, such as migration, Number of accidents and free-forming small Group size. It has been observed that the ZTPD gives much closer fits than ZTPLD in almost all cases except the distribution of the number of household having at least one migrant in Table 15.
X |
Observed frequency |
Expected frequency |
ZTPD |
ZTPLD |
1 |
375 |
354.0 |
379.0 |
2 |
143 |
167.7 |
137.2 |
3 |
49 |
53.0 |
48.4 |
4
5
6
7
8 |
17
2
2
1
1 |
|
16.8
|
Total |
590 |
590.0 |
590.0 |
ML Estimate |
|
|
|
|
|
8.933 |
1.031 |
d.f. |
|
2 |
3 |
P-value |
|
0.0115 |
0.7937 |
Table 15 Number of households having at least one migrant according to the number of migrants, reported by Sing & Yadav.30
Number of accidents |
Observed frequency |
Expected frequency |
ZTPD |
ZTPLD |
1 |
2039 |
2034.2 |
2050.4 |
2 |
312 |
319.5 |
291.7 |
3
4
5 |
35
3
1 |
33.5
2.6
0.2 |
41.1
5.8
1.0 |
Total |
2390 |
2390.0 |
2390.0 |
ML Estimate |
|
|
|
|
|
0.387 |
3.128 |
d.f. |
|
1 |
1 |
P-value |
|
0.5339 |
0.0769 |
Table 16 Number of workers according to the Number of accidents, reported by Mir & Ahmad31
Number of pairs of running shoes |
Observed frequency |
Expected frequency |
ZTPD |
ZTPLD |
1 |
18 |
17.7 |
24.1 |
2 |
18 |
18.5 |
15.0 |
3 |
12 |
12.9 |
9.0 |
4
5 |
7
5 |
|
5.2
6.2 |
Total |
60 |
60.0 |
60.0 |
ML Estimate |
|
|
|
|
|
0.191 |
3.998 |
d.f. |
|
2 |
3 |
P-value |
|
0.9089 |
0.2617 |
Table 17 Number of counts of pairs of running shoes owned by 60 members of an athletics club, reported by Simonoff.32
Group size |
Observed frequency |
Expected frequency |
ZTPD |
ZTPLD |
1 |
1486 |
1500.5 |
1592.8 |
2 |
694 |
669.6 |
551.8 |
3 |
195 |
199.2 |
186.5 |
4 |
37 |
44.4 |
61.9 |
5
6 |
10
1 |
|
|
Total |
2423 |
2423.0 |
2423.0 |
ML Estimate |
|
|
|
|
|
2.702 |
66.155 |
d.f. |
|
3 |
3 |
P-value |
|
0.4399 |
0.0 |
Table 18 Number of free forming small Group size according to the Group size, reported by Coleman & James33
Group size |
Observed frequency |
Expected frequency |
ZTPD |
ZTPLD |
1 |
316 |
316.4 |
335.8 |
2 |
141 |
140.7 |
116.0 |
3 |
44 |
41.7 |
39.1 |
4
5 |
5
4 |
|
|
Total |
510 |
510.0 |
510.0 |
ML Estimate |
|
|
|
|
|
0.558 |
12.481 |
d.f. |
|
2 |
2 |
P-value |
|
0.7565 |
0.0019 |
Table 19 Number of free forming small Group size according to the Group size, reported by Coleman & James33
Group size |
Observed frequency |
Expected frequency |
ZTPD |
ZTPLD |
1 |
306 |
302.5 |
322.5 |
2 |
132 |
139.5 |
114.6 |
3 |
47 |
42.9 |
39.7 |
4
5 |
10
2 |
|
|
Total |
497 |
497.0 |
497.0 |
ML Estimate |
|
|
|
|
|
0.834 |
8.220 |
d.f. |
|
2 |
2 |
P-value |
|
0.6590 |
0.0164 |
Table 20 Number of free forming small Group size according to the Group size, reported by Coleman & James33
Group size |
Observed frequency |
Expected frequency |
ZTPD |
ZTPLD |
1 |
305 |
307.2 |
327.7 |
2 |
144 |
142.9 |
117.3 |
3 |
50 |
44.3 |
40.9 |
4
5
6 |
5
2
1 |
|
|
Total |
507 |
507.0 |
507.0 |
ML Estimate |
|
|
|
|
|
2.376 |
17.806 |
d.f. |
|
2 |
2 |
P-value |
|
0.3048 |
0.0001 |
Table 21 Number of free forming small Group size according to the Group size, reported by Coleman & James33
Conclusion
In this paper, the nature and behavior of ZTPD and ZTPLD have been studied by drawing different graphs for the different values of its parameter. A general expression for the  th factorial moment has been given and the first four moments about origin has been obtained. Also a very simple and easy method for finding moments of ZTPLD has been suggested. An attempt has been made to study the goodness of fit of both ZTPD and ZTPLD to count data relating to demography, biological sciences, and social sciences and it has been found that ZTPLD is a better model than the ZTPD in almost all data-sets relating to mortality and biological sciences whereas ZTPD is a better model than ZTPLD in almost all data-sets relating to social sciences.. Thus, ZTPLD has an advantage over ZTPD for modeling zero-truncated count data in mortality and biological sciences whereas ZTPD has an advantage over ZTPLD for modeling zer-truncated count data in social sciences.
th factorial moment has been given and the first four moments about origin has been obtained. Also a very simple and easy method for finding moments of ZTPLD has been suggested. An attempt has been made to study the goodness of fit of both ZTPD and ZTPLD to count data relating to demography, biological sciences, and social sciences and it has been found that ZTPLD is a better model than the ZTPD in almost all data-sets relating to mortality and biological sciences whereas ZTPD is a better model than ZTPLD in almost all data-sets relating to social sciences.. Thus, ZTPLD has an advantage over ZTPD for modeling zero-truncated count data in mortality and biological sciences whereas ZTPD has an advantage over ZTPLD for modeling zer-truncated count data in social sciences.
Acknowledgments
Conflicts of interest
References
- Sankaran M. The discrete Poisson‒Lindley distribution. Biometrics. 1970;26:145‒149.
- Shanker R, Hagos F. On Poisson‒Lindley distribution and Its Applications to Biological Sciences. Biometrics and Biostatistics International Journal. 2015;2(4):1‒5.
- Lindley DV. Fiducial distributions and Bayes’ Theorem. Journal of the Royal Statistical Society. 1958;20:102‒107.
- Ghitany ME, Atieh B, Nadarajah S. Lindley distribution and Its Applications. Mathematics and Computers in Simulation. 2008a;78(4):493‒506.
- Ghitany ME, Al‒Mutairi DK. Estimation Methods for the discrete Poisson‒Lindley distribution. Journal of Statistical Computation and Simulation. 2009;79(1):1‒9.
- Shanker R, Mishra A. A two‒parameter Poisson‒Lindley distribution. International Journal of Statistics and Systems. 2014;9(1):79‒85.
- Shanker R, Mishra A. A two‒parameter Lindley distribution. Statistics in Transition new Series. 2013 a;14(1):45‒56.
- Shanker R, Mishra A. A quasi Poisson‒Lindley distribution (submitted). 2015.
- Shanker R, Mishra A. A quasi Lindley distribution. African journal of Mathematics and Computer Science Research. 2013b;6(4):64‒71.
- Shanker R, Sharma S, Shanker R. A Discrete two‒Parameter Poisson Lindley Distribution. Journal of Ethiopian Statistical Association. 2012;21:15‒22.
- Shanker R, Sharma S, Shanker R. A two‒parameter Lindley distribution for modeling waiting and survival times data. Applied Mathematics. 2013;4:363‒368.
- Shanker R, Tekie AL. A new quasi Poisson‒Lindley distribution. International Journal of Statistics and Systems. 2014;9(1):87‒94.
- Shanker R, Amanuel AG. A new quasi Lindley distribution. International Journal of Statistics and Systems.2013;8(2):143‒156.
- Shanker R, Hagos F, Sujatha S. On modeling of Lifetimes data using exponential and Lindley distributions. Biometrics and Biostatistics International Journal. 2015;2(5):1‒7.
- Plackett RL. The truncated Poisson‒ distribution. Biometrics. 1953;9:185‒188.
- David FN, Johnson NL. The truncated Poisson. Biometrics. 1952;8:275‒285.
- Cohen AC. An extension of a truncated Poisson distribution. Biometrics. 1960a;16:446‒450.
- Cohen AC. Estimation in a truncated Poisson distribution when zeros and some ones are missing. Journal of American Statistical Association. 1960b;55:342‒348.
- Tate RF, Goen RL. MVUE for the truncated Poisson distribution. Annals of Mathematical Statistics. 1958;29:755‒765.
- Ghitany ME, Al-Mutairi DK, Nadarajah S. Zero‒truncated Poisson‒Lindley distribution and its Applications. Mathematics and Computers in Simulation. 2008b;79(3):279‒287.
- Meegama SA. Socio‒economic determinants of infant and child mortality in Sri Lanka, an analysis of postwar experience. International Statistical Institute (World Fertility Survey), Netherland. 1980.
- Lal DN. Patna in 1955 A Demographic Sample Survey. Demographic Research Center, Department of Statistics, Patna University, Patna, India. 1955.
- Mishra A. Generalizations of some discrete distributions. Unpublished Ph.D thesis, Patna University, Patna, India. 1979.
- Garman P. The European red mites in Connecticut apple orchards. Connecticut Agri Exper Station Bull. 1923;252:103‒125.
- Student. On the error of counting with a haemacytometer. Biometrika. 1907;5(3):351‒360.
- Finney DJ, Varley GC. An example of the truncated Poisson distribution. Biometrics. 1955;11:387‒394.
- Khursid AM. On size‒biased Poisson distribution and its use in zero truncated case. J KSIAM. 2008;12(3):153‒160.
- Matthews JN, Appleton DR. An application of the truncated Poisson distribution to Immunogold assay. Biometrics. 1993;49(2):617‒621.
- Keith LB, Meslow EC. Trap response by snowshoe hares. Journal of Wildlife Management. 1968;32:795‒801.
- Singh SN, Yadava KN. Trends in rural out‒migration at household level. Rural Demogr. 1981;8(1):53‒61.
- Mir KA, Ahmad M. Size‒biased distributions and their applications. Pak J Statist. 2009;25(3):283‒294.
- Simmonoff JS. Analyzing Categorical data. Springer, New York. 2003.
- Coleman JS, James J. The equilibrium size distribution of freely‒forming groups. Sociometry. 1961;24(1):36‒45.

© . This is an open access article distributed under the terms of the,
which
permits unrestricted use, distribution, and build upon your work non-commercially.



![]() th factorial moment has been given and the first four moments about origin has been obtained. Also a very simple and easy method for finding moments of ZTPLD has been suggested. An attempt has been made to study the goodness of fit of both ZTPD and ZTPLD to count data relating to demography, biological sciences, and social sciences and it has been found that ZTPLD is a better model than the ZTPD in almost all data-sets relating to mortality and biological sciences whereas ZTPD is a better model than ZTPLD in almost all data-sets relating to social sciences.. Thus, ZTPLD has an advantage over ZTPD for modeling zero-truncated count data in mortality and biological sciences whereas ZTPD has an advantage over ZTPLD for modeling zer-truncated count data in social sciences.
th factorial moment has been given and the first four moments about origin has been obtained. Also a very simple and easy method for finding moments of ZTPLD has been suggested. An attempt has been made to study the goodness of fit of both ZTPD and ZTPLD to count data relating to demography, biological sciences, and social sciences and it has been found that ZTPLD is a better model than the ZTPD in almost all data-sets relating to mortality and biological sciences whereas ZTPD is a better model than ZTPLD in almost all data-sets relating to social sciences.. Thus, ZTPLD has an advantage over ZTPD for modeling zero-truncated count data in mortality and biological sciences whereas ZTPD has an advantage over ZTPLD for modeling zer-truncated count data in social sciences.