Characteristics of respondents
A total of 1,381 questionnaires were returned. After excluding those with too many missing values, especially in clinical area variables, the main interest of this study, 1,142 questionnaires were analyzed. As depicted in (Table 2), most of the survey respondents (73.7%) were female, which is understandable in that most nurses in Korea are female and the number of nurses is much larger than the number of physicians. Health care professionals with 5 to 10 years of experience (25.4%) formed the largest group and were followed by those with 3 to 4 years (21.8%). The tails on both sides of work years accounted for the smallest proportion at 6.7% for respondents with less than 6 months of experience and 5.3% for those with 21 years or more. For job type, nurses constituted the majority at 53.3%, followed by physicians at 33.1%. Supporting staff was 11.6% of the respondents and there was a small number of pharmacists, administrators, and uncategorized HCWs.

The results and fit indices of CFA are provided in (Table 3 & 4). To help readers better understand the CFA results, items in (Table 3) are shown in English as the original SAQ, although actual survey administration and analysis used SAQ-K. GFI, NFI, and CFI were higher than 0.9, AGFI was 0.894, and RMSEA was less than 0.05, indicating a good model fit based on commonly used criteria._29,30.

Effects of clinical area on the score of SAQ-K domains
(Table 5) shows the overall means $\beta$  and standard deviations $\varphi$  of the six SAQ-K domain scores from model 0; the overall means$\beta$  and standard deviations $\tau$ of the clinical area random effect around the overall mean, and standard deviations $\sigma$ of residuals of SAQ-K scores around the clinical area-specific mean for each of the six domains from (model 1).

The means$\beta s$ of both models were similar, ranging from approximately 55 (WC) to 69 (SR). Among the six domains, JS showed the largest standard deviation of random effects,$\tau ,$ at 7.84, and SR showed the smallest $\tau ,$ at 3.29. Though$\tau ,$ appeared smaller than the standard deviation $\sigma$ of the residuals within clinical areas for all six domains, the LR test results showed that random effects were statistically significant for all six domains, suggesting that SAQ-K scores differed by clinical area and thus clinical area-specific SAQ-K scores are worth estimating.

Empirical Bayesian estimation of SAQ-K domain scores by clinical area
To obtain more accurate estimates of clinical area-specific means, we applied the empirical Bayesian method. (Figure 2) shows the means estimated for the TC domain by ordinary least square (OLS) regression (upper panel) and the EB method (lower panel). Each bar stands for the mean and 95% confidence interval (CI) of a clinical area. The numbers over the CI bars are the clinical area ID numbered by the rank of OLS means; ten clinical areas with the widest CIs by OLS were marked, and these area IDs were marked on the EB means and CIs to clearly show the changes.

For those ten clinical areas, CIs hugely shrunk and their ranks changed, indicating that area mean estimates from the EB method differed from OLS results. Note that any changes in rank were toward the center, the overall TC score mean that was around 65, as denoted in (Table 5). These findings exemplify the shrinkage idea of the EB method, where clusters with large variance borrow information from other clusters to yield more accurate estimates; in other words, CIs become narrower. In return, the means from the EB method are pulled toward the overall mean even to the level at which the rank orders change significantly.

Figure 2 Posterior distributions of the TPRs and the missing data under conditional independence of the tests.

Figure 3 Work area means and 95% confidence intervals of all six domains of SAQ-K.

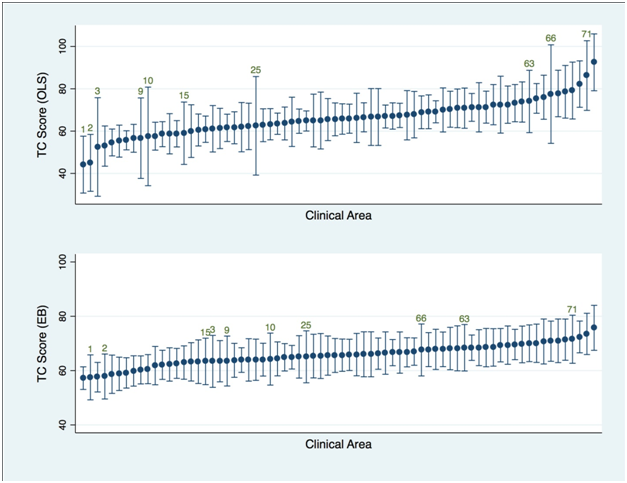
Figure 3 shows the estimates from OLS and the EB method side by side for all six domains, helping the reader understand the effects of the EB method in obtaining more accurate estimates. Due to space limits, IDs of only seven clinical areas are displayed. Although the TC domain was shown in (Figure 2), we show it again to better compare the results.

The primary aim of this study was to develop and validate SAQ-K. The results showed that SAQ-K had acceptable internal consistency and construct validity, suggesting that it is ready for use in health care organizations across Korea. Note that two items from the original SAQ, one in the TC domain and the other in PM, were excluded in the final version of SAQ-K. These two items were negatively phrased and their Korean translation was hard for respondents to answer, which emphasizes the difficulty of cross-cultural adaptation of an instrument and the need for exceptional caution.²⁶

One reason we want to measure safety culture is to predict future safety incidents. Indeed, many studies have shown that safety improvement programs with a component that nurtures safety culture have significantly reduced the incidence rates of harmful events.^2,31 Therefore, hospital safety managers naturally ask, “Which areas of my hospital have a low safety culture?” The answer to this question guides resource allocation for safety improvement efforts across various areas of the hospital. In this sense, the more accurate the SAQ scores we obtain, the better we can allocate resources, which will eventually enable a hospital to get the most out of its safety programs.

Traditional approaches have simply calculated the mean and standard deviation of SAQ domain scores by clinical area, and more likely they only calculated the percentage of respondents with positive perceptions. Both of these approaches are limited in use by overly small sample sizes in many clinical areas. As shown in Figure 1, several clinical areas have only a few HCWs working in them and, therefore, the clinical area mean of such units cannot be estimated accurately due to large standard deviations, as shown in (Figures 2 & 3). However, in the most cases, those simple traditional approaches have prevailed, probably because safety managers more often than not have limited statistical background, especially in advanced statistics like the Bayesian approach.

This study, therefore, applied the empirical Bayes method to provide more accurate mean SAQ domain scores for each clinical area. The empirical Bayes predictor is the best linear unbiased predictor (BLUP), and in this study the EB method improves the accuracy of area-specific estimates by borrowing strengths from other clinical areas.²² In this process, the mean of each area shrinks toward the overall mean, yielding results as seen in the lower panel of (Figure 2). The advantage of the EB method is that it can be applied even when there are clusters contain very small sample sizes, like one or two,^22-24,32 which is frequently the case in hospitals in Korea.

Despite the above-mentioned statistical strengths of the EB method, one might point out overlaps in the CIs of clinical areas and therefore this EB approach might not be necessary. Though seemingly logical, this doubt is easily resolved if one understands how SAQ scores are used in hospitals. Due to the scarcity of resources, a hospital can run safety improvement programs like teamwork training only for a certain number of clinical areas (e.g., ten units in a given year). Selection of those ten units is based on SAQ scores (e.g., bottom ten areas), regardless of whether CIs overlap or not. Therefore, estimating mean SAQ scores of clinical areas as accurately as possible is essential to guaranteeing the just allocation of resources. In addition, SAQ is usually measured annually, leading safety managers to examine changes in SAQ scores by clinical area over time. One might consider building a longitudinal model with the SAQ score of each HCW as the unit of analysis. However, in most cases, this can be challenging because new HCWs are joining and also many HCWs are leaving the area. This naturally leads us to use the mean SAQ score of a clinical area as the unit of analysis, where a sound longitudinal model can only be built with accurate mean SAQ scores of clinical areas.

Before we applied the EB method, we tested whether SAQ scores were significantly different among clinical areas. This step was particularly important in this study in that it guided us in judging whether EB estimates were worth applying. For a dataset with not many clusters, one-way ANOVA can be used, but this study covered 72 clinical areas which were heavily unbalanced in sample sizes and had unequal variance, as seen in (Figures 1 & 2). Therefore, we built variance components models with clinical area-level random effect and tested the difference by observing whether the random effect was statistically significant. In this study, we used the likelihood-ratio test because we were only interested in whether the random effect model was necessary, as seen in (Table 5). If the estimates of CIs for random effect are of interest, score tests (Lagrange multiplier tests) can be used instead.^22,33 Employing variance components models is useful, especially when multiple clustering factors are of interest, such as clinical areas and job type of HCW. In an earlier section, how resources can be allocated over clinical areas was introduced, and the same logic can be applied to job type instead of clinical area. The problem arises when a safety manager needs to decide which clustering factors between clinical area and job type should be used for resource allocation. To illustrate, if variance in TC scores over job type is much bigger than that over clinical area, then the manager can develop a program for the job type with the lowest TC score to match other job types with higher TC score.³⁴

 The variance components model allows us to perform such comparison between variances. For example, by expanding the above variance component model, a crossed random effects model can be built on the assumption that the SAQ score of an HCW is correlated with both clinical area and job type, without assuming hierarchy between clinical area and job type. We can test whether each of the clustering criteria is significant and compare their variances. Also, we can test whether the effect of job type is nested within a clinical area, or the other way around, with hierarchical models. If there are only a few different job types in a hospital and just marginal differences in SAQ scores among job types are of interest, a generalized estimating equation (GEE) with clinical area as the clustering variable³⁵ can be used. Though building a GEE model is relatively simple, it is not discussed in this study because it is not within the scope of the study.

Although we developed and validated SAQ-K successfully and provided methodology for its analysis, some issues remain to be addressed. First, many HCWs work in multiple areas of the hospital. For example, a physician in the Department of Anesthesiology and Clinical Care Medicine (ACCM) works in both operating rooms and intensive care units. Which clinical area should the physician choose? A more fundamental question might be which area one perceives as the culture in which one is embedded. SAQ defines one’s clinical area as the area where one ‘typically’ spends time, but this is not clear for many HCWs. Also, sufficient time is required for an HCW to be assimilated into an area’s culture. If the period from when an HCW begins to work in an area to SAQ administration is only one week, it might not be wise to think that the HCW’s responses accurately reflect the area. In hospitals where HCWs frequently change their working areas or where new trainees join regularly, this issue is amplified. These issues probably cannot be solved perfectly. Rather, what we can do is maintain consistency across the hospital. For example, a SAQ participant inclusion criterion in the Johns Hopkins Hospital is “HWCs with a 50% commitment to one clinical area for at least 4 consecutive weeks before the survey administration”¹⁷ Though still arbitrary, this offers better internal validity when a comparison of SAQ scores within a hospital is of interest.

Culture is complex issue. Measuring culture, therefore, is rightly difficult, and safety culture in hospitals is no exception. However, such difficulty cannot justify our negligence in measuring it. Indeed, without measuring safety culture, we will never be able to improve it. Thus, instruments to measure safety culture are crucial. Through this study, we developed the Korean version of such measurement tool, and we also developed methodologies to better analyze it; these methodologies can be used in other countries as well. We hope that this study helps Korean hospitals provide patients in Korea with safer care, the care that patients well deserve.

Contact the corresponding author at hjeong1@jhu.edu for SAQ-K and Stata commands for the analyses in this article.