eISSN: 2378-315X


Short Communication Volume 1 Issue 2
University of Copenhagen, Denmark
Correspondence: Niels Lynnerup, Laboratory of Biological Anthropology, University of Copenhagen, Institute of Forensic Medicine, Frederik d's Vej 11, 2100 Copenhagen, Denmark, Tel 45 35327239
Received: November 11, 2014 | Published: November 24, 2014
Citation: Johansson S, Simonsen E, Lynnerup N. Determination of knee joint centre by Ct-scanning. Biom Biostat Int J. 2014;1(2):47-51. DOI: 10.15406/bbij.2014.01.00011
In gait analysis the center of the knee joint is used for the calculations that define anatomically based reference systems. Usually, anatomical landmarks are defined on the knee surface, and these coordinates are then used to calculate the knee joint center. However, most calculations are based on equations based on X-rays of one single person. Here we present knee joint center calculations based on CT-scans of 40 corpses. Coordinates for anatomical landmarks, over which skin markers are placed, were registered and used to calculate the location of the joint center following the conventional equation. Using a three-dimensional representation of the CT-scan, the joint center was also estimated visually. The locations of the visually estimated and calculated joint center were compared to each other. The results show that with the calculated joint center as a reference, the location of the visually estimated joint center is on average 16.41mm (SD 5.75) dorsal, 4.59mm (SD 2.21) lateral and 16.59mm (SD 5.07) distal to the calculated center. These results show a systematic deviation between the location of the calculated and visually estimated joint center. The systematic deviation may form the basis for a new equation for calculation of the knee joint center.
Keywords: joint centre, ct-scanning, biomechanics, gait analyses
Diseases that affect the skeleton muscular system or in other ways affect the ability to walk may result in a characteristic gait. Gait analysis is currently used in diagnostics and research regarding such diseases, e.g., central or peripheral affection of the motor nervous system, muscular diseases, impaired proprioception and cerebellar affection.1–3 Gait analysis is also used in improvement and research concerning sports activities4,5 and in forensic anthropology as a tool in personal identification.6,7 Central in much gait analyses is the determination of the joint centre, which affects how joint movement is interpreted in gait recording and modelling. However, when perusing papers regarding gait analysis, the methods for calculating the center of the joints are often not precisely described or there is only a reference to a computer program2,4,8,9 In those papers where the method is in fact more precisely described there is a reference to Grood & Suntay,10 A joint coordinate system for the clinical description of three-dimensional motions: applications to the knee.10 Examples are Wu and Cavanagh,11 Dierks et al.,5 Astephen Wilson et al.,12 Apkarian et al.,13 Favre et al.14
Gait analysis can be performed in different ways. The most frequently used methods use external markers placed on the skin. The gait is then recorded on video from different angles simultaneously and the recorded data is processed in specialised computer programs.
In this article we use a model based gait analysis method from Vaughan et al.,1 This method uses 15 external markers, placed on the skin over anatomical landmarks. Subsequently the gait is recorded from six angles and the data is processed by using specific algorithms. The calculations require the exact position of the center of the hip, knee and ankle joints. The equation that is used to find the center of the knee joint is based on measures from one single person.1 Here we test if data collected from 40 CT-scans can validate this equation.
The material consists of 40 whole-body, computed tomography (CT) scans, performed on corpses brought to our institute for forensic autopsy. Pre-autopsy scanning is standard procedure (scanning parameters: mA, V, slice thickness). All CT-scans pertained to males, the age span was 20-87years (mean=52).The material only comprises corpses without pathology or lesions to the lower limbs.
When calculating the position of the knee joint center we used the method described in Vaughan et al.,1 where the basic variables include the diameter of the knee (measured as the maximum width at the level of the femoral epicondyles) and the spatial coordinates of the lateral epicondyle (marker 5), the tuberosity of the tibia (marker 4) and the lateral malleolus (marker 3). All calculations are based on measurements on the right limb. By using a computer program, Mimics (Materialise®, Levwen, Belgium), the bone structures were segmented from the CT-scan and the result is a three dimensional reconstruction of the bones in the lower limbs (Figure 1a). The measurements and coordinates are plotted on the 3D-reconstruction (Figure 1b-1d) and saved in the program to be used for later calculations. For reasons of consistency due to possible putrefactive changes in the soft tissues, we plotted the external markers as being directly on the bone surface and not on the skin as the external markers commonly used in gait analysis, but on a subsample of 10 Ct-scans we measured the error introduced by this.

The position of the knee joint center is calculated from the coordinates of the three markers plotted on the bones. An orthogonal reference system (u,v,w) is created based on the markers positions relative to one another. The origin of the coordinate system is at the position of the lateral epicondyle and the three axes (u,v,w) are perpendicular to one another. The three markers form a plane and the axis w is perpendicular to this plane. v is parallel to a line connecting marker 3 and 5 and the axis u is perpendicular to these two axes. A mathematical equation can be used to calculate the center of the knee joint.1
where:
p3, p4 and p5 are three dimensional coordinates of the lateral malleolus, the tibial tubercle and the femoral epicondyle, respectively.
In addition to the calculations the knee joint center are also visually estimated (Figure 2) using the 3D-reconstruction and Mimics tools for measuring diameters. The position of the center of rotation is on an axis between the femoral condyles.15,16 I addition to this, the mechanical conditions in form of the curvature of the individual epicondyles are taken into consideration in the estimation. The center of rotation is found by drawing two tangents to the curvature. The point where the normal"s to these two tangents meet is on the same axis as the center of rotation.15
Finally the positions of the visually estimated and the calculated joint center are compared to see if there is a systematical deviation. First the calculated joint center is plotted in Mimics and the distance between the estimated and the calculated center is measured in millimeters. The limbs are not in the exact same position in the scanner so to be able to see an actual deviation in relation to the bone structure we define the anatomical planes (Figure 3) and measure the distance between the estimates center and the calculated center in the anatomical planes respectively (Figure 4).
By comparing the x-, y- and z- coordinates for the visually estimated knee joint center and the coordinates of the calculated joint center it is clear that the results of the two methods are different. The deviation can be shown by subtracting the estimated coordinates from the calculated coordinates. The overall, average deviation is: x=-2.09mm (SD 5.58), y=-15.91mm (SD 5.19) and z=14.82mm (SD 5.19). The coordinates are comparable within the same CT-scan, but the limbs are not placed in completely identical positions in the scanner. This means that it is more appropriate for the further analysis if the deviation is shown in well defined anatomical planes (Figure 5).
With the calculated knee joint center as a standard it is shown that the position of the visually estimated joint center (Table 1) is 16.41mm dorsal (SD 5.75), 4.59mm lateral (SD 2.21) and 16.59mm distal (SD 5.07) to the calculated center (Figure 6). This systematic deviation can form the basis for a new equation.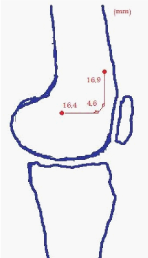
Disk |
S |
F |
T |
3 |
-20.55 |
+8.06 |
-24.18 |
8 |
-14.05 |
+3.53 |
-18.24 |
9 |
-16.69 |
+5.77 |
-14.04 |
10 |
-17.14 |
+3.06 |
-9.79 |
11 |
-14.96 |
+4.83 |
-8.34 |
14 |
-24.97 |
0.00 |
-13.53 |
15 |
-36.22 |
+2.89 |
-8.19 |
16 |
-10.23 |
+4.29 |
-20.11 |
17 |
-16.65 |
+4.68 |
-8.81 |
19 |
-17.55 |
+1.25 |
-22.36 |
20 |
-13.87 |
+6.93 |
-5.24 |
21 |
-11.77 |
+2.75 |
-21.58 |
22 |
-19.19 |
+3.66 |
-19.09 |
23 |
-17.40 |
+6.28 |
-12.21 |
24 |
-24.01 |
+2.76 |
-21.12 |
25 |
-14.00 |
+6.93 |
-12.98 |
26 |
-13.85 |
+5.62 |
-16.64 |
27 |
-19.27 |
+6.69 |
-12.12 |
28 |
-15.29 |
+2.91 |
-18.68 |
29 |
-14.78 |
+2.80 |
-14.60 |
30 |
-9.46 |
+1.30 |
-17.53 |
31 |
-15.62 |
+4.02 |
-15.43 |
32 |
-17.38 |
+5.03 |
-8.91 |
33 |
-18.99 |
+3.22 |
-15.04 |
34 |
-20.23 |
+3.24 |
-25.21 |
35 |
-18.03 |
+7.46 |
-11.42 |
36 |
-18.08 |
+3.72 |
-17.45 |
37 |
-8.43 |
+9.11 |
-14.86 |
38 |
-9.60 |
+2.02 |
-20.94 |
39 |
-19.10 |
+5.75 |
-21.67 |
40 |
-12.37 |
+2.75 |
-20.11 |
42 |
-20.48 |
+4.77 |
-19.11 |
43 |
-7.84 |
+5.44 |
-25.44 |
44 |
-8.96 |
+6.53 |
-15.71 |
45 |
-11.49 |
+5.84 |
-18.32 |
46 |
-13.14 |
+6.59 |
-15.25 |
47 |
-17.14 |
+8.61 |
-16.66 |
48 |
-19.66 |
+4.89 |
-19.82 |
49 |
-8.20 |
+7.25 |
-18.06 |
50 |
-29.56 |
+0.56 |
-24.66 |
Table 1 Where the estimated center is placed compared
When analysing the results based on data from 40 bodies it can be concluded that there is a systematic deviation between the positions of the knee joint centre when using the two different methods of visual estimation and calculation using equations that is currently used in gait analysis.1
The knee is a composite, pivotal hinge joint. It allows flexion and extension as well as rotation when the knee is flexed.17 Because of the complexity of the knee, the center of rotation moves relative to the bone structure. Viewed from the sagittal plane, the articular bodies are not symmetric; the curvature is greater in the dorsal part of the condyles. This results in the center of rotation migrating in a distal and dorsal direction along with the flexion movement.17
Normally the markers are placed on the skin, since it has to be a non-invasive procedure. Here the markers are placed directly on to the bone structure. External skin markers where considered and it would have been possible with the transparent 3D image where skin and bone can be given different colors, but soft tissue changes fast due to putrefactation and we lack data about how long the bodies have been laying in room temperature before stored in cooled areas. The conclusion was that markers placed directly on the bone would provide a more valid and useful result. To investigate what effect this might have on our results we randomly chose 10 CT scans and measured the distance between skin and bone over the three relevant markers. The distance from skin to bone over the lateral malleolus was in average 1.6mm (0.8-3.7mm), over the tuberositas of tibia in average 2.2mm (0.8-4.1mm) and over the lateral epicondyle the skin-bone distance was in average 9.9mm (4.1-18.9mm). Those numbers are too small to explain the dorsal and distal deviation of approximately 16mm. It might however be the explanation of the 4.6mm deviation in lateral direction. To see if the distance from skin to bone is bilaterally symmetric over the two epicondyles we also measured the skin to bone distance over the medial epicondyle. The result was an average of 10.2mm (5.3-20.8mm). That means that the difference between the two sides is 0.3mm which cannot explain the 4.6mm deviation. Furthermore, the CT image are not showing a person who is putting weight on the leg, which would have been more close to a natural walk.
A way to precede this work would be to use the results to find a new equation for analysing the biomechanics of the knee. Doing corresponding studies with the hip and ankle joints would provide to an improvement of gait analysis as a whole. The migration of the centre of rotation in relation to the angle of flexion contributes to an uncertainty regarding the results. Working with dynamic data would be a methodological improvement. If working with corpses, the CT scan can be repeated with increasing angles of flexion. If it is possible to replace CT with MRI (Magnetic Resonance Imaging) living test persons can be used, since there are no exposure to radiation. Additionally it may be more accurate if dynamic data is collected when weight is put on the leg in the stance phase and the leg is hanging free in the swing phase, as in a natural walk.
The conclusion of this work is that with our visual estimation the joint centre is placed dorsal, distal and lateral to the calculated joint centre. The new data can originate in a new equation for calculating the position of the knee joint centre. It is interesting to find out what effect such a new equation would have on the results of the gait analysis. This can be explored by comparing the results of a gait analysis conducted in a classic way with the analysis of the same gait after the algorithms has been changed. When doing this a potential discrepancy can be detected and the new equations actual effect on the gait analysis can be evaluated.
It should be noted that women and children are not represented in this study. Another limitation is that some diseases and injuries that give a characteristic gait also result in, or are the result of, structural changes in the knee. An equation based on data from healthy individuals may not be valid for individuals with relevant diseases. The ultimate but resource demanding solution would be to collect data from each patient group individually
None.
Author declares that there are no conflicts of interest.
None.

©2014 Johansson, et al. This is an open access article distributed under the terms of the, which permits unrestricted use, distribution, and build upon your work non-commercially.
2 7