
Correspondence:
Received: January 01, 1970 | Published: ,
Citation: DOI:
Download PDF
Abstract
Evaluating the effect of a treatment on a time to event outcome is the focus of many randomized clinical trials. It is often observed that the treatment effect is heterogeneous, where only a sub group of the patients may respond to the treatment due to some unknown mechanism such as genetic polymorphism. In this paper, we propose a semi parametric exponential tilt mixture model to estimate the proportion of patients who respond to the treatment and to assess the treatment effect. Our model is a natural extension of parametric mixture models to a semi parametric setting with a time to event outcome. We propose a nonparametric maximum likelihood estimation approach for inference and establish related asymptotic properties. Our method is illustrated by a randomized clinical trial on biodegradable polymer delivered chemotherapy form malignant gliomas patients.
Keywords: exponential tilt model, mixture model, time to event data, treatment heterogeneity, randomized clinical trial
Abbreviations
ETM, exponential tilt model; ETMM, exponential tilt mixture model; NPMLE, non parametric maximum likelihood estimation; BCNU, bis-chloroethyl nitro sourea
Introduction
Survival time is a primary end point for assessing the treatment effect in many randomized clinical trials. It is often observed that the treatment may only be effective to a sub group of the population due to some unknown mechanism such as genetic polymorphism. For patients in that sub group, which we call responders; their survival time is associated with the treatment assignment. For patients not in that subgroup, which we call non responders, their survival time follows the same distribution regardless of the treatment assignment. One such example is from a randomized trial conducted by Brem et al.,
1 Two hundred and twenty two recurrent brain malignant gliomas patients were randomized to receive either bio degradable polymer delivered bis-chloroethyl nitro sourea (BCNU), a chemotherapy, or place bowafers at the time of primary surgical resection. The histograms of survival time comparing the BCNU treated group and the place bogroup are shown in (Figure1). The histogram for the BCNU group appears to be a mixture of two uni-mode distributions, where one of the two modes is at roughly the same location as the mode for the place bogroup. Therefore, the BCNU treatment effect on patients" survival appears to be heterogeneous, the distribution of survival time in the treatment group is a mixture of two uni-mode distributions, one for non-responders and the other for responders. Clinically, three questions are of great interest. First, what is the proportion of responders in the population? Second, how to estimate the treatment effect for responders? Third, how to test the existence of treatment effect? (
Figure 1).
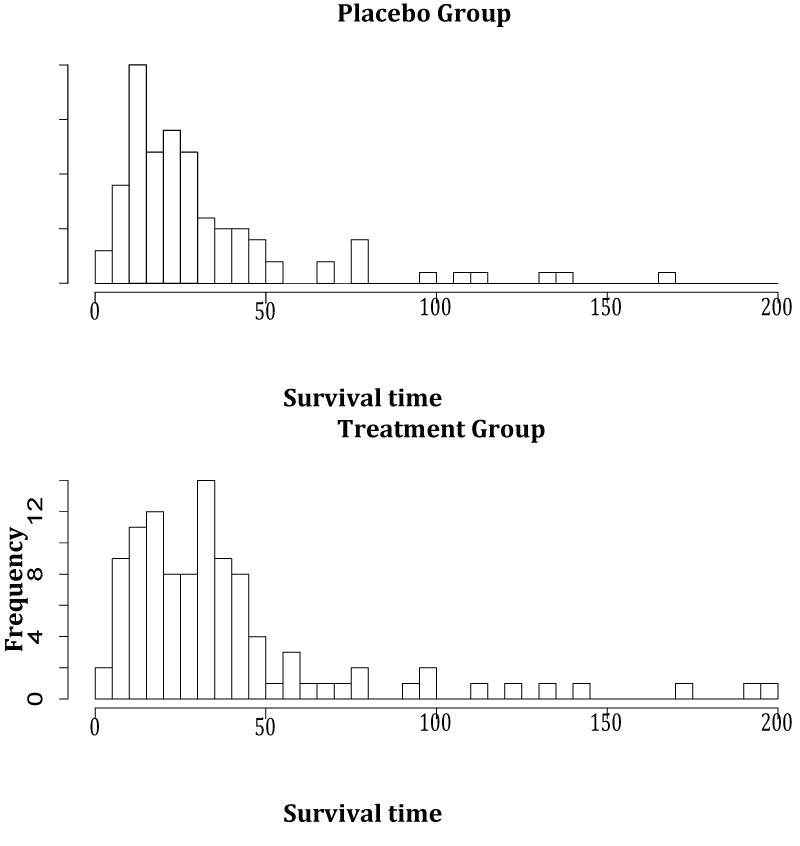
Figure 1 Histograms of the BCNU data.
One approach to analyze data with a mixture structure is by using finite (parametric) mixture models,2 where each mixture component was assumed to follow a parametric distribution and the EM algorithm was used to find maximum likelihood estimates of the distribution al parameter and the mixture proportion. Larson & Dinse3 and McLachlan4 extended the parametric mixture models to handle survival data with censored observations. See McLachlan & McGiffin5 for a review of the development in this field. More recently, semi parametric models have become an interesting alternative because of the more flexible model frame work and weaker model assumptions. The proportional hazards model, which is the most frequently used semi parametric model for survival data, has been extended to handle mixture data.6,7 However, one concern of using the proportional hazards mixture model is that it does not have clear connections to parametric mixture models except for the Weibull mixture model.
For completely observed data, another interesting semi parametric model, referred to as the Exponential Tilt Mixture Model (ETMM), has been proposed by Qin8 and Zou et al.,9 This model is based on the Exponential Tilt Model (ETM), which assumes alog-linear function for the density ratio of two mixture components, leaving the base line density unspecified. The ETM accommodates abroad class of parametric models because the density ratio functions from many parametric models, such as normal model, gamma model, and log normal model, have very simple forms that can be easily modelled by a log-linear function. Built up on the ETM, the ETMM can be viewed as a natural generalization of parametric mixture models. The ETM without a mixture structure has been extended to censored, time-to-event data Shen et al.,10 Wang et al.11 However, to our knowledge, the extension of ETMM to time-to-event outcome has not been studied yet.
One important issue for mixture models is testing for the existence of treatment effect. This hypothesis testing problem is not regular because the parameter space is degenerated under the null hypothesis. The asymptotic distribution of the regular likelihood ratio test statistic is very complicated Hartigan,12 Chen & Chen.13 Alternatively, Chen14 proposed a penalized likelihood ratio test, which solved the degenerate problem by adding a penalizing term to the likelihood function. The asymptotic distribution of the test statistic turned out to be much simpler. However, there is no clear standard on how to choose an appropriate penalizing function. Lemdani & Pons15 and Liang & Rathouz16 proposed another testing method based on the following observation although jointly testing for two parameters, the mixture proportion and the distributional parameter of the mixture component, is not regular, the test for one parameter given the other is regular. By utilizing this nice property, they proposed testing statistics with very simple asymptotic distributions for binomial mixture models.
In this paper, we extend the ETMM to censored, time-to-event data. We propose a non parametric maximum likelihood estimation (NPMLE) approach to estimate model parameters and study the associated asymptotic properties. We also develop a statistical testing procedure to assess the existence of treatment effect based on the ETMM. The application of our methods is illustrated by using the BCNU data.
Materials and methods
Exponential tilt mixture model (ETMM)
Letis
the distribution of survival time in the control group. As for the treatment group, to characterize the hetero generous treatment effect for responders and non responders, we assume the survival time follows a mixture distribution:
where 1−λ is the proportion of responders and
is the distribution of survival time for responders after receiving the treatment. We consider an ETM for the treatment effect on responders:
, where h(t, β) is a pre specified parametric function with a vector of parameters β. Our model is semi parametric because
is completely unspecified. The ETMM can be regarded as a semi parametric generalization of parametric mixture models. For example, it reduces to the normal mixture model with two mixture components if F0 is a normal distribution and
.
Parameter estimation
We assume the survival time and the censoring time are independent given treatment assignment and further assume the censoring time to be discrete with a finite number of values
for the control group and
for the treatment group. Let
. Suppose the observed data consist of
uncensored, independent observations x1,… ,xn, where the first n0 observations come from the place bogroup with density
and the next n1 come from the treatment group with density
. The data also contain m0 censored, independent observations from the place bogroup and m1, and independent observations from the treatment group, with mzj observations censored at time
. Let
and
be the numbers of observations in the two groups
and be the total number of observations. Furthermore,
. In this sub section, we assume there is a treatment effect so that λ<1. We will discuss the test for the existence of treatment effect in Section 2.3. Our parameters of interest include the mixture proportion λ and the distributional parameter β characterizing the difference between the two mixture components. Now consider discrete distributions with point masses only at the observed failure times and let
. Then on parametric log likelihood function17,18 is:
With a constraint
let
and define the profile likelihood of θ as
. The NPMLE of θ is obtained by maximizing
, that is,
. One appealing feature of the NPMLE method is that it does not have the problem of “unbounded likelihood”. Day19 pointed out that, for normal mixture models, the global MLE may not exist because the likelihood goes to infinity if one mixture component concentrates on a single sample point. This problem does not arise in our non parametric likelihood approach. By considering discrete distributions, the point mass at any sample point is almost one, which yields a bounded likelihood. In practice,
can be obtained via the EM algorithm,20 see Supplementary Materials for the details. Then,
can be obtained via Newton-Raphson method by maximizing
. The asymptotic properties of
are as follows:
Proposition 1: Assume that all the elements in
,
and
are continuous and bounded by some function
for
in a neighbourhood of the true value of β satisfying
and
. We have
I.
is a consistent estimator of θ
II.
Where θ the true parameter is value and
is the Fisher information.
Proof: See Supplementary Materials.
To estimate survival probabilities for responders and non responders at a give time point
, it is natural to consider the following estimators
Where
is the
that maximize
in equation (1). Proposition 2 shows that the survival probability estimators
for non responders and
for responders in the treatment group) are a symptotically linear, which can be used to calculate standard errors of the estimators and to construct point wise confidence intervals for survival functions.
Proposition 2: Under the same conditions as in Proposition 1,
Where the expression of
is defined in equation (S5) in Supplementary Materials.
Proof: See Supplementary Materials.
Testing the existence of treatment effect
There are two equivalent ways to express the null hypothesis for testing the existence of treatment effect. One way, expressed as λ=1, is to test whether the data come from a mixture of two distributions or from a single distribution. The other way, expressed as β=0, is to test whether the two mixture components are the same. The diversity in expressing the null hypothesis indicates their regularity of this testing problem. Under the null hypothesis, the joint parameter space for (λ, β) is degenerated. It includes two lines λ=1 and β is arbitrary, and β=0 and λ is arbitrary. The asymptotic distribution for the regular likelihood ratio statistics very complicated.
In this sub section, we propose a simple solution to this problem based on the observation that under the null hypothesis, if we fix one parameter, testing for the other parameter is regular. The idea is an alog us to Lemdani and Pons15 Liang and Rathouz16 used for parametric mixture models. Two tests can be constructed
- one is the likelihood ratio test for β with affixed λ
- The other is the likelihood ratio test for λ for with a fixed β.
These two tests correspond to the two different yet equivalent expressions of the null hypothesis: β=0 and λ=1. Since λ is simply a scaler and easy to be set to affixed value, for convenient, we will focus on testing β=0 for a fixed λ.
Proposition 3: Under the same conditions as in Proposition 1, for any given,
,
where
is the NPMLE of β for a given λ and
is the profile likelihood under the null hypothesis. Proof: See Supplementary Materials.
In practice, it is also of interest to estimate the proportions of non responders and responders by constructing a 95% confidence interval for λ. However, the regular Wald confidence interval constructed from Proposition 2 may underestimate λ because it always excludes one based on the assumption of λ<1 we made in the proposition. Alternatively, we consider the following procedure:
i. Perform the test in Proposition 3. If the p-value is smaller than 0.05, go to step 2; otherwise, go to step 3.
ii. Construct the regular Wald confidence interval, which is
.
iii. Construct the confidence interval as
.
Where
is the q quantile of the asymptotic distribution of
. When λ<1, the confidence intervals in both Step 2 and Step 3 can cover λ with probability 0.95.When λ=1, there is 95% of the chance to choose the interval in Step3, which always contains one. Thus, the fore mentioned procedure can always covert the true value of λ with probability 0.95.
Results
Simulations
The first set of simulations evaluates the finite sample performance of the estimate or for the mixture proportion λ. We considered the first three simulation scenarios listed in (Table 1). Specifically, λ was chosen as 0.25, 0.50 or 0.75, representing different proportions of responders in the treatment group. Observations in the place bogroup were simulated from alog-normal distribution
, and those in the treatment group were simulated from
, where
. The simulation setting is similar to the BCNU data in the sense that the distribution of survival time for responders in the treatment group has larger mean and smaller variance than that for nonresponders. We assumed censoring to occur at 6 fixed time points, the 30%, 40%, 50%, 60%, 70% and 80% quantile of F0. The censoring probabilities were 14% for the place bogroup and 16% to 20% for the treatment group, depending on the mixture proportion. Separate simulations were run for
15 or 500. Under each setting, 1,000 independent data sets were simulated. We considered the following two specifications of the h(.) function in the ETM:
The first h(.) function is proportional to the density ratio for log-normal distributions. The corresponding ETM, which we call the log-normal ETM, reduces to alog-normal model when F0 is alog normal distribution. The second h(.) function is a more general expression that in corporate density ratios for log-normal, exponential, and gamma distributions. The corresponding ETM is called the general ETM. Simulation results are summarized in (Table 1 & 2).
|
Scenario
|
F0
|
F1
|
|
|
(i)
|
LN(3.2,0.92)
|
LN(3.7,0.22)
|
0.25
|
|
(ii)
|
LN(3.2,0.92)
|
LN(3.7,0.22)
|
0.50
|
|
(iii)
|
LN(3.2,0.92)
|
LN(3.7,0.22)
|
0.75
|
|
(iv)
|
LN(3.2,0.92)
|
LN(3.2,0.92)
|
—
|
Table 1 Simulation scenarios
|
Simulation
|
Log-normal ETM
|
General ETM scenario
|
|
|
N0=N1
|
Bias
|
SSE
|
SEE
|
CP
|
Bias
|
SSE
|
SEE
|
CP
|
|
(i)
|
150
|
−0.002
|
0.061
|
0.056
|
0.94
|
−0.012
|
0.063
|
0.058
|
0.95
|
|
500
|
−0.002
|
0.031
|
0.031
|
0.95
|
-0.005
|
0.031
|
0.031
|
0.96
|
|
(ii)
|
150
|
−0.014
|
0.093
|
0.078
|
0.94
|
−0.035
|
0.112
|
0.083
|
0.94
|
|
500
|
-0.002
|
0.041
|
0.042
|
0.95
|
-0.006
|
0.043
|
0.043
|
0.95
|
|
(iii)
|
150
|
−0.100
|
0.211
|
0.219
|
0.88
|
−0.150
|
0.253
|
0.173
|
0.89
|
|
500
|
−0.011
|
0.065
|
0.066
|
0.92
|
−0.024
|
0.095
|
0.063
|
0.91
|
Table 2 Simulation results for estimating
Bias is the mean difference between and the true value, SSE is the standard error of , SEE is the square root of the mean of the variance estimate of , and CP is the coverage probability of the 95% confidence interval of
For λ=0.25 or 0.50, estimates from both the log-normal ETM and the general ETM are virtually unbiased. Coverage probabilities are also close to the desired value 0.95.For λ=0.75 and when sample size is small (
=150), biases are large and coverage probabilities are lower than 0.95. This is due to the limited number of responders in the data. The estimation becomes better when the sample size increases to 500.
The second set of simulations evaluates the performance of the testing statistic
proposed in Section 2.3. We considered the same three scenarios as in the first set of simulations. In addition, we considered a null scenario where both
and
. The simulation scenarios are listed in (Table1). We used the log-normal ETM as our working model and considered five choices of λ in
: 0.00, 0.25, 0.50, 0.75 and 0.90. Results are summarized in (Table 3).
The power appears to be higher for larger λ. For example, the empirical power is 1.00 for λ = 0.90 in simulation scenario with
= 500. But the power for λ = 0.00 is only 0.75. However, the test statistic with larger λ is also less stable. The type I error is larger than the expected value when λ = 0.75 or 0.90
and = 150.
Data analysis
Malignant gliomas are a common type of malignant primary brain tumors. Despite of the disproportionately high morbidity and mortality, drug treatment is hampered by the difficulty in crossing the blood-brain barrier and the severe complications from systemic exposure to drugs targeted for the brain. To overcome these problems, a method was developed to incorporate BCNU, a very effective chemotherapeutic drug, into biodegradable polymers. Implantation of the BCNU-incorporated polymers at the tumor site allows local sustained release of BCNU with minimal systemic exposure. In a clinical trial conducted by Brem et al.,1 two hundred and twenty two patients with recurrent malignant brain tumors were randomized in to a BCNU-treatment group and control group. Patients" survival time was recorded. In this section, we evaluate the effectiveness of BCNU treatment and estimate the proportion of patients that benefited from the treatment (Table 4).
We consider two ETMs: the log-normal ETM and the general ETM. The results are summarized in (Table 4). Since the likelihood ratio test comparing the two ETMs is not significant (p-value=0.168), we choose the log-normal ETM as our working model. Based on this model, we test the hypothesis of no treatment effect (β=0) using the test statistic LRT λ(λ) described in Proposition 3. Fixing λ at 0.00, 0.25, 0.50, 0.75, or 0.90, we obtain the p-value as 0.38, 0.36, 0.29, 0.10, or 0.12. The test with smaller λ seems to be less powerful, which is consistent with our simulation findings in Section 3. Since none of the tests is significant at 5% level, we follow Step 3 of the procedure described in Section 2.3 to calculate a 95% confidence interval for λ as (0.595,1). The survival function estimates for the first year of follow-up comparing treatment responders vs. non responders are shown in (Figure 2). The survival fraction for treatment responders is significantly higher than that for non responders in the first thirty weeks. But after that period, the survival fractions for the two sub groups become close.
|
Scenario
|
N0=N1
|
LRTλ(0)
|
LRTλ(0.25)
|
LRTλ(0.5)
|
LRTλ(0.75)
|
LRTλ(0.9)
|
|
(i)
|
150
|
1.00
|
1.00
|
1.00
|
1.00
|
1.00
|
|
500
|
1.00
|
1.00
|
1.00
|
1.00
|
1.00
|
|
(ii)
|
150
|
0.86
|
0.94
|
0.99
|
1.00
|
0.99
|
|
500
|
1.00
|
1.00
|
1.00
|
1.00
|
1.00
|
|
(iii)
|
150
|
0.28
|
0.32
|
0.52
|
0.77
|
0.70
|
|
500
|
0.75
|
0.78
|
0.87
|
0.99
|
1.00
|
|
(iv)
|
150
|
0.04
|
0.04
|
0.05
|
0.09
|
0.15
|
|
500
|
0.05
|
0.05
|
0.05
|
0.06
|
0.11
|
Table 3 Empirical Type I error/power for testing the existence of treatment effect
|
|
|
SE
|
95% Confidence interval
|
Log-likelihood
|
|
Log-normal ETM
|
0.804
|
0.099
|
(0.595,1)
|
-1151.355
|
|
General ETM
|
0.738
|
0.111
|
(0.524,1)
|
-1150.405
|
Table 4 Analysis results for the BCNU data. SE is the estimated error of
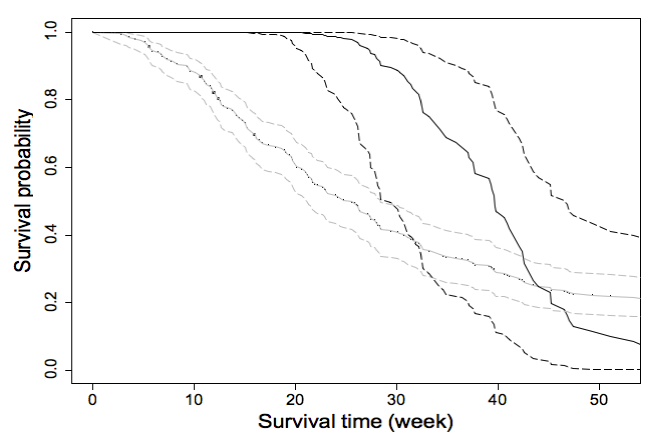
Figure 2 Estimated survival functions (solid curves) along with 95% confidence intervals (dashed curves) for the BCNU data. The black curves are for responders in the treatment group, and the gray curves are for non-responders.
Conclusion
In this paper, we investigate the treatment effect heterogeneity problem in randomized clinical trials, where the survival time for only a subgroup of the population is affected by the treatment. To deal with this problem, we extend the ETMM to time-to-event out come. We also develop a testing procedure for the existence of treatment effect. To characterize the magnitude of heterogeneity, we proposed a unified confidence interval for the mixture proportion.
One limitation of our method is that it assumes a sufficiently long follow-up period. In case of a short follow-up period with patients censored by the end of the study, anew parameter to characterize the survival fraction by the end of the study can be introduced. Statistical inference procedure and theoretical proofs will need to be modified correspondingly. Similar approach has been taken in Wang et al.11,21 Another limitation of our method is that the censoring time is assumed to be discrete. Extending our method to continuous censoring time is challenging due to the technical complexity in studying asymptotic properties of model parameters. More advanced theoretical tools, such as the modern empirical process, may be required. But the derivations are primarily of mathematical interest because censoring time can be approximated by a sufficiently fine set of discrete points in practice.
The power of
depends on the choice of λ. Based on simulations, we recommend to use λ = 0.50, which balances the sensitivity and stability. More powerful tests may be derived by taking the supreme over λ. For binomial mixture model, Lemdani and Pons15 showed that the supreme test
, 0<e<1 has the same asymptotic distribution as
for a given λ. The asymptotic distribution of the supreme test under the ETMM is more complicated. But the empirical distribution may be obtained using a re-sampling method.
Acknowledgments
Conflicts of interest
Authors declare that there are no conflicts of interests.
Funding
References
- Brem H, Piantadosi S, Burger PC, et al. Placebo-controlled trial of safety and efficacy of intra operative controlled delivery by bio degradable polymers of chemotherapy for recurrent gliomas. The Polymer-brain Tumor Treatment Group. Lancet. 1995;345(8956): 1008–1012.
- Pearson K. Contributions to the mathematical theory of evolution. Phil Trans R Soc Lond A. 1894;185:71–110.
- Larson MG, Dinse GE. A mixture model for the regression analysis of competing risks data. Appl Statist. 1985;34(3):201–211.
- McLachlan GJ. Mixture models and applications. In: Balakrishnan N, Basu AP, editors. USA: The Exponential Distribution: Theory, Methods and Applications. CRC Press; 1996.
- McLachlan GJ, McGiffin DC. On the role of finite mixture models in survival analysis. Statistical Methods in Medical Research. 1994;3(3):211–226.
- Rosen O, Tanner M. Mixtures of proportional hazards regression models. Stat Med. 1999;18(9):1119–1131.
- Chen HY, Little RJA. Proportional hazards regression with missing covariates. Journal of the American Statistical Association. 1999;94(447):896–908.
- Qin J. Empirical likelihood ratio based confidence intervals for mixture proportions. The Annals of Statistics. 1999;27(4):1368–1384.
- Zou F, Fine JP, Yandell BS. On empirical likelihood for a semi parametric mixture model. Biometrika. 2002;89(1):61–75.
- Shen Y, Qin J, Costantino JP. Inference of tamoxifen’s effects on prevention of breast cancer from a randomized controlled trial. J Am Stat Assoc. 2007;102(480):1235–1244.
- Wang C, Tan Z, Louis TA. Exponential tilt models for two-group comparison with censored data. Journal of Statistical Planning and Inference. 2007;141(3):1102–1117.
- Hartigan JA. A failure of likelihood a symptotics for normal mixtures. In: Le Cam LM, Olshen RA, editors. USA: Proceedings of the Berkeley Conference in Honor of Jerzy Neyman and Jack Kiefer, Wadsworth Publishing Co Inc; 1985. p. 1950.
- Chen H, Chen J. Large sample distribution of the likelihood ratio test for normal mixtures. Statistics & Probability Letters. 2001;52(2):125–133.
- Chen J. Penalized likelihood-ratio test for finite mixture models with multinomial observations. The Canadian Journal of Statistics. 1998;26(4):583–599.
- Lemdani M, Pons O. Tests for genetic linkage and homogeneity. Biometrics. 19985;51(3):1033–1041.
- Liang KY, Rathouz PJ. Hypothesis testing under mixture models: Application to genetic linkage analysis. Biometrics. 1999;55(1):65–74.
- Vardi Y. Empirical distributions in selection bias models (Com:P204-205). Ann Statist. 1985;13(1):178–203.
- Owen AB. Empirical Likelihood. USA: Chapman & Hall Ltd; 2001.
- Day NE. Estimating the components of a mixture of normal distribution. Biometrika. 1969;56(3):463–474.
- Dempster AP, Laird NM, Rubin DB. Maximum likelihood from in completed data via the EM Algorithm. Journal of the Royal Statistical Society. 1997;39(1):1–38.
- Wang C, Tan Z, Louis TA. An exponential tilt model for quantitative trait loci mapping with time-to-event data. Journal of Bioinformatics Research Studies. 2014.

© . This is an open access article distributed under the terms of the,
which
permits unrestricted use, distribution, and build upon your work non-commercially.


