Plants response to temperature is an important issue. In order to determine cardinal temperatures and its related germination responses to temperature three varieties seeds of milk thistle (Shomal, Mollasani and Majarestan) were exposed to six constant temperatures (10, 15, 20, 25, 30 and 35°C) in a four replicated factorial arranged, completely randomized design. Results indicated that the temperature and variety had a significant effect on the maximum germination percentage (MGR), germination uniformity (GU), germination rate (reciprocal time to 50% germination), and time to 5, 10, 50, 90 and 95% germination, but the interacted effect of temperature and variety was not significant. Assessment of three non-linear regression models, including segmented, dent-like and beta models revealed that the beta model was an appropriate model for all varieties. Base and ceiling temperatures for all three varieties were estimated at near to 0 and 40°C, respectively. Optimum temperature for Shomal, Mollasani and Majarestan varieties was estimated as (28.79, 29.97 and 29.58°C), respectively. Biological time for 50% germination for Shomal, Mollasani and Majarestan varieties also was estimated at 43.61, 42.61 and 45.85hours, correspondingly. It was concluded that these model can be used to quantify response of milk thistle germination to temperature and to obtain cardinal temperature of germination. These parameters are required to predict milk thistle germination and emergence.

Keywords: beta model, cardinal temperature, biological time, milk thistle, phenology

MGR, maximum germination percentage; GU, germination uniformity; GR, germination rate; RMSE, root mean square of errors; CV, coefficient of variation; R², coefficient of determination; T_b, base temperature; T_o, optimum temperature; T_o1, lower limit of optimum temperature; T_o2, upper limit of optimum temperature; T_c, ceiling temperature; Fo, biological time; MGP, maximum germination percentage

Milk thistle (Silybum marianum L.) is one of the most important medicinal plants in the pharmaceutical industry worldwide, and is used in the production of flavonoids of the silymarin group (silybin, silidianin and silychristine). The origin of this plant has been reported to be the East Mediterranean region.¹ In this century, extensive research has been conducted on medicinal plants, and medicines that contain natural active ingredients have opened new horizons for the community of physicians and pharmacists engaged in research. Therefore, the pharmaceutical industry and research groups of many countries have turned their attention to the cultivation and production of medicinal plants.²

Given the importance of these plants in the provision of medicines required by people, the collection, and the completion of, information concerning the ecophysiological behaviors of these plants becomes a necessity. This research was conducted to evaluate non-linear regression models for describing germination responses of milk thistle to temperature, and to estimate the cardinal temperatures of its germination.

Germination is the first and the most important stage in plant development and is influenced by genetic and environmental factors.^3,4 Germination and establishment of seedlings are among the critical and important stages in the life cycle of plants.⁵ Seed germination is the first stage in plant growth and consists of the three steps of water absorption, lag phase and root emergence. Enzymatic activity starts in the first and second steps. During the second step, respiration increases, degradation, and synthesis reactions are started and activated, enzymes break down stored tissues and transfer materials, and finally, in the third step, radicles appear.⁶

Temperature and moisture can affect germination percentage and rate either singly or in combination.⁷ If sufficient moisture and oxygen are provided, temperature determines the characteristics of mass germination (such as rate, uniformity and percentage of germination) of non-dormant seeds,^8–12 and the effects of temperature on plant development are the basis for models that predict germination timing.¹³ Temperature is the most important driving force influencing crop development rate.¹⁴

In 1860, it was found that plants have base or minimum, optimum and maximum or ceiling germination temperatures. The minimum or base temperature is the lowest temperature at which germination happens. The optimum temperature is the temperature with the highest germination rate and the maximum or ceiling temperature is the highest temperature at which seeds can germinate.^12,15,16 Cardinal temperatures may significantly differ in various species and varieties.¹⁷

Each plant germinates in a specific temperature range known as cardinal temperatures,¹⁸ which includes minimum, optimum and maximum temperatures that have applications in presenting models for predicting germination.¹² Plant growth rate increases with temperature rises from the base to the optimum temperatures and declines from the optimum to the ceiling temperatures.¹⁹ Temperature not only affects germination percentage but also germination rate.²⁰ Since temperature has considerable effects on germination characteristics, such as the start of percentage and germination percentage and rate, it is, therefore, the most critical factor determining the success or failure of plant establishment.²¹

Seeds of different plants respond to temperature differently. Germination rate and percentage reach their maximums at the optimum temperature and decline to zero at the ceiling and the base temperatures.²² Some studies suggest that, normally, germination rate increases linearly, at least in a suitable temperature range, but falls sharply at temperatures exceeding this range.²³ It is useful to study seed germination and emergence responses to temperature because it allows us to determine the cardinal temperatures for creating models that can predict seed germination and emergence and for selecting the suitable planting time. It also enables us to select species and genotypes that are able to tolerate low or high temperatures and to determine geographical regions where plant species and genotypes can germinate and establish successfully.^11,12

Models play an important role in structuring data and ideas, and can determine the weak areas, and the gaps, in our knowledge. A plant model is a mathematical description of our understanding concerning plant behavior and, since mathematics is used in the creation of the model, it must be completely clear and specified at all stages.²⁴ Therefore, some researchers have used these models to obtain the cardinal temperatures, that is, the base, the optimum, and the ceiling temperatures.^23,25 There are various functions for describing germination responses to temperature, among which three have been used more often: the segmented, the beta, and the dent-like functions.^19,26,27

Kamkar et al.,²⁸ in their study of poppy by using non-linear regression models, recommended the segmented model as the superior model for predicting germination rate. Kamkar et al.,^14,15 also used segmented and logistic models to determine cardinal temperatures of germination in 3millet varieties and emergence in wheat cv. “Tajan”. Jame et al.,²⁹ used the beta model in their study on quantification of germination and emergence of spring wheat. Khalili³⁰ also used non-linear regression models to quantify germination rate responses of barley to temperature and to water potential, and recommended the beta model as the superior one. Ghaderi-Far et al.,³¹ in their evaluation of non-linear regression models for the three medicinal plants of pumpkin, brago and black cumin, concluded that the dent-like model described germination rate responses to temperature better than other models.

This experiment was conducted at the laboratory of Seed Research of Gorgan University of Agriculture and Natural Resources in 2012 using a factorial arrangement of treatments and randomized complete block design in four replications. The experimental treatments included three cultivars of milk thistle (Shomal, Mollasani, and Majarestan) and six levels of temperature (10, 15, 20, 25, 30 and 35degrees centigrade). Incubators with the accuracy of 0.5degree centigrade were used for the temperature treatments. Each experimental unit consisted of a petri dish (9-cm diameter) in which 50 milk thistle seeds were placed on top of two sheets of filter paper and were covered by a single sheet of filter paper. Subsequently, depending on the temperature used, the numbers of germinated seeds at different time intervals were counted. Obviously, this interval will be shorter for temperatures closer to the optimum one. At each interval, the germinated seeds were removed. The criterion for germination was a radical emergence of two millimeters or more. Counting was stopped when no seeds germinated within 48hours, or when all the seeds had germinated. Each time the germinated seeds were counted, the exact time of counting was recorded. During the experiment, distilled water was added to the petri dish when required.

The GS-2011 software (Kamkar, 2011) was used to extract the deciles of germinations. The software fitted seed germination data from these temperature regimes to the logistic function and performed the necessary calculations through interpolation. Moreover, germination rate (per hour) was determined by using formula 1:¹⁹

$GR=\frac{1}{D_{50}}$(1)

In the above formula, GR is the germination rate and D₅₀ the time it takes for 50percent of the seeds to germinate.

In this study, three temperature functions were compared to describe changes in germination rate against temperature. These functions were:

1. The Beta function, shown by the abbreviation B, is as follows:¹⁹

$f(T)=\frac{[(\frac{T-T_b}{T_o-T_b})\ast (\frac{T_c-T}{T_c-T_b})(\frac{T_c-T_o}{T_o-T_b})]\alpha }{f_o}$...(2)

2. The Dent-like function, shown by the abbreviation D, is as follows:¹⁹

$$f\left(T\right)=\frac{\left(T-T_b\right)}{\left(T_{o1}-T_b\right)} if T_b<T\le T_{o1}$$

$f\left(T\right)=\frac{\left(T-T_b\right)}{\left(T_{o1}-T_b\right)} if T_{o2}<T\le T_c$(3)

$$f\left(T\right)=1 if T_{o1}<T\le T_{o2}$$

$$f\left(T\right)=0 if T\le T_b orT\ge T_c$$

3. The Segmented function, shown by the abbreviation S, is as follows¹⁹

$$f\left(T\right)=\frac{\left(T-T_b\right)}{\left(T_o-T_b\right)} if T_b<T<T_o$$

$f\left(T\right)=\left[\frac{1-\left(T-T_o\right)}{\left(T_c-T_o\right)}\right] if T_o<T<T_c$...(4)

$f\left(T\right)=0 ifT\le T_b orT\ge T_c$

In the above function, Tb is the base temperature, To1 the lower limit of optimum temperature, To2 the upper limit of optimum temperature, To the optimum temperature, Tc the ceiling temperature, Fo the biologic time, “a” a constant coefficient, and T the average daily temperature (the temperature at which the experiment was conducted).

Parameters of each model were estimated by a method of iterative optimization with the help of the PROC NLIN procedure of the SAS software.³² In this method of iterative optimization, every time the initial values of the parameters are entered, the final value is estimated by the least-squares method. Initial values are changed until the best estimate of the parameters is obtained. The root mean square of errors (RMSE) of germination time, the coefficient of determination (R²), the correlation coefficient (r), the simple linear regression coefficients a and b, and the relationship between the observed and the predicted germination rates were used to select the superior model from among the employed methods.

The higher the coefficient of determination (R²) is, the higher the percentage of changes in germination rate explained by the model. Coefficients “a” and “b” represent the degree of deviation of the regression line from the origin of coordinates and the bias of the regression line from the 1:1 line, respectively. The SAS software determined the numerical values of coefficients “a” and “b.” Significance of coefficient “a” was investigated by SAS and that of coefficient “b” by determining confidence limits. If coefficient “a” is significant, it means that the y-intercept of the regression line and the y-intercept of the 1:1 line do not coincide. If coefficient “b” is significant, it means that the slopes of the regression line and that of the 1:1 line are different and that the regression line is biased, in relation to the 1:1 line.³³ The less the points are scattered around the 1:1 line, the more efficient the model is. Given these criteria, the superior model was used to determine the cardinal germination temperatures for describing germination rates of various milk thistle varieties.

Results of analysis of variance of mean squares of maximum germination percentage (MGR), of germination uniformity (GU), of germination rate (GR), and of the time of reaching 5% (D5), 10% (D10), 50% (D50), 90% (D90) and 95% (D95) germination showed that the effects of temperature on all of the mentioned parameters were significant at the one percent probability level. Varieties did not affect the parameter of reaching 5% germination, but had significant effects on the time of reaching 50% and 90% germination at the one percent level of probability and exhibited significant effects on other parameters at the five percent level of probability. Moreover, the mutual effects of variety and temperature on the parameter of germination uniformity at the one percent level of probability, and on the parameter of reaching 90% germination at the five percent level of probability, were significant (but these mutual effects did not significantly influence the other parameters) (Table 1). Nadjafi et al.,³⁴ studied 11 medicinal plant species and reported that the maximum percentage and rate of milk thistle germination were obtained in the temperature range of 10-30degrees centigrade. The reduction in germination percentage and rate at non-optimal temperatures can be attributed to the reduction or inhibition of, enzymatic activity and, hence, to a reduction in the required rates of biosynthetic reactions that necessary for germination at these temperatures.³⁵ It is expected that high temperatures cause seed deterioration in addition to reducing germination rate.²⁵

The beta and the segmented models estimate the base, the optimum, and the ceiling temperatures and the biological time, while the dent-like model estimates the range of optimum temperatures (from the lower limit of optimum temperature to the upper limit of optimum temperature). The criteria used in comparing different models for selecting the superior one to be used in describing germination responses to temperature in various varieties of milk thistle include root mean square of error (RMSE), the coefficient of determination (R²), the regression coefficients “a” and “b”, and the relationship between the observed germination rate and the predicted one (Table 2).

Results obtained from comparison of these criteria are as follow:

In the Shomal variety, the “b” coefficient (the bias of the regression line from the 1:1 line) was not significant in any of the three models, and its value in the beta model (0.97) was closer to one compared to the other two models. Moreover, the “a” coefficient (the degree of deviation of the regression line from the origin of the coordinates) in the beta and dent-like models was not significant, but it was significant in the segmented model at the five percent probability level. The coefficient “a” in the beta model (0.0003) was closer to zero compared to the other two models. The coefficient of determination (R²) in the beta model (99%) was higher compared to the other two models. The root mean square error (RMSE) and the coefficient of variation (CV) in the beta model (0.0006 and 3.9 respectively) were less compared to the other two models (Table 2). The points around the 1:1 line were less scattered in the beta model compared to the other two models. Taking the above points into consideration, and since the “a” coefficient was significant in the segmented method, this model was eliminated in the selection of the superior model for the Shomal variety. The root of mean square error, the coefficient of variation, and the scattering of the points around the 1:1 line were lower in the beta model compared to the dent-like model. Therefore, the beta model was selected as the superior model for the Shomal variety and was used in later stages to determine the cardinal temperatures (Figure 1).

In the Mollasani variety, the “b” coefficient (the bias of the regression line from the 1:1 line) was not significant in any of the three models, and its value in the beta model (0.99) was closer to one compared to the other two models. Moreover, the “a” coefficient (the degree of deviation of the regression line from the origin of the coordinates) in the beta and dent-like models was not significant, but it was significant in the segmented model at the five percent level of probability. The “a” coefficient in the beta model was 0.00007 and closer to zero than in the other two models. The coefficient of determination (R²) in the beta model (99%) was higher compared to the other two models (Table 2). The root mean square error (RMSE) and the coefficient of variation (CV) in the beta model (0.0003 and 3.72, respectively) were less compared to the other two models. The points around the 1:1 line in the beta model was less scattered compared to the other two models. Considering the above points, and because the “a” coefficient was significant in the segmented model, this model was eliminated in the selection of the superior model. The root of mean square error, the coefficient of variation, and the scattering of points around the 1:1 line were less, and the coefficient of determination was higher, in the beta model compared to the dent-like model. Therefore, the beta model was selected as the superior model for the Mollasani variety and was used in later stages to determine the cardinal temperatures (Figure 2).

In the Majarestan variety, the “b” coefficient (the bias of the regression line from the 1:1 line) in none of the three models was significant, and its value in the beta model (0.99) was closer to one compared to the other models. Moreover, the “a” coefficient (the degree of deviation of the regression line from the origin of the coordinates) was not significant in any of three models, and its value in the beta model (- 0.000006) was closer to zero compared to the other two models. The coefficient of determination (R²) in the beta and segmented model, 99%, was higher compared to the dent-like model. The root mean square error (RMSE) and the coefficient of variation (CV) in the beta model (0.0004 and 3.27 respectively) were less compared to the other two models (Table 2). The points around the 1:1 in the beta model were less scattered compared to the other two models. The root mean square error, the coefficient of variation, and the degree of the scattering of the points around the 1:1 lines were less, and the coefficient of determination was higher in the beta model compared to the other two models. Therefore, considering what was earlier said, the beta model was selected as the superior model for the Majarestan variety too, and was used in later stages to determine the cardinal temperatures (Figure 3).

Figure 1 The relationship between germination speed and temperature (in degrees centigrade), The predicted values for 50% germination obtained by using the beta (B), the dent-like (D), and the segmented (S) functions are presented against the observed value in the Shomal variety.

Figure 2 The relationship between germination speed and temperature (in degrees centigrade), The predicted values for 50% germination obtained by using the beta (B), the dent-like (D), and the segmented (S) functions are presented against the observed value in the Mollasani variety.

Figure 3 The relationship between germination speed and temperature (in degrees centigrade), The predicted values for 50% germination obtained by using the beta (B), the dent-like (D), and the segmented (S) functions are presented against the observed value in the Majarestan variety.

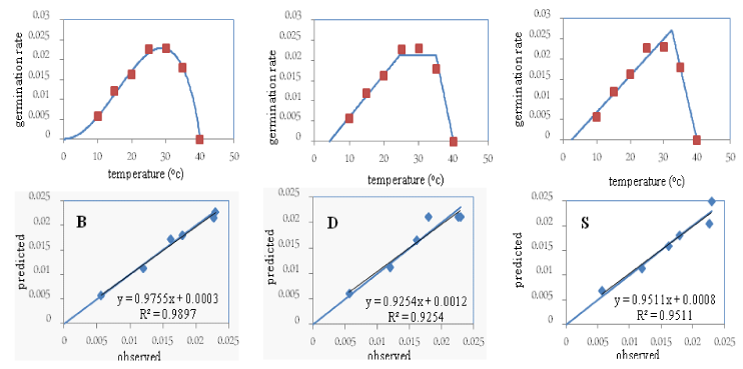
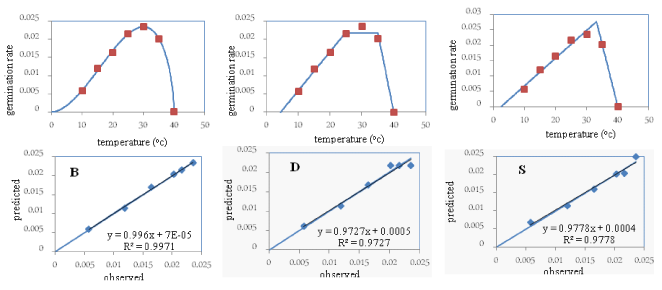
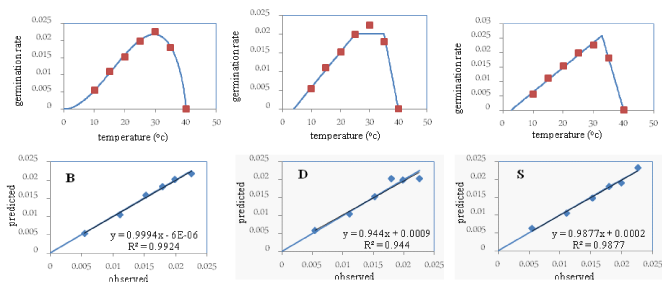
Since the beta model was selected as the superior model for all three studied varieties, its parameters including the base, the optimum, and the ceiling temperatures were used for all three varieties. Based on obtained results:

The estimated base temperatures were 0.00000001, 0.0602, and 0.00000001degree centigrade for the Shomal, the Mollasani, and the Majarestan varieties, respectively. The estimated optimum temperature for the Shomal variety was 28.79degrees centigrade, and 29.97 and 29.58degrees centigrade for the Mollasani and the Majarestan varieties, respectively. The estimated ceiling temperature for all three varieties was 40degrees centigrade. Moreover, the biological time for 50% germination was equivalent to 43.61, 42.61, and 45.85hours for the Shomal, Mollasani, and Majarestan varieties, respectively (Table 3).

Researchers have reported the cardinal temperatures of many plants. Nadjafi et al.,³⁴ in a study on cardinal temperatures of germination of 11 medicinal plants, reported that the base, optimum, and ceiling temperatures for milk thistle (Silybum marianum) were 2.7, 18 and 40.3degrees centigrade, respectively. In cornflower (Centaurea benedicta), they were 0, 13, and 35.5, in hyssop (Hyssopus officinalis) 0, 17.8 and 44.6 in marrubium (Marrubium vulgare) 4, 17.8 and 42.6, and in raceme catnip (Nepeta racemosa), 1.3, 24.1 and 42.6 degrees centigrade. The cardinal temperatures were 3.4, 22.5 and 42.5 degrees centigrade in common evening primrose (Oenothera biennis), 4, 23.2 and 41.3 in basil (Ocimum basilicum), 1, 18.4 and 40.1 in marjoram (Origanum majorana). The cardinal temperatures were 0, 21 and 40.3degrees centigrade in sage (Salvia sclarea), 0, 17 and 41 in sage (Salvia nemorosa), and 3.1, 22.7 and 42.4degrees centigrade in thyme (Thymus daenensis subsp. Daenensis). Kamkar et al.,²⁸ in a study they conducted on poppy, found its base, optimum and ceiling temperatures for germination were 3.02, 27.36 and 36.31degrees centigrade, respectively. Jami Al-Ahmadi et al.,²¹ in their research on finding the cardinal temperatures of germination in the species kochia (Kochia scoparia), reported that it could germinate in a wide range of temperatures from 3.5 (the base temperature) to 50 (the ceiling temperature), with its optimum germination temperature being 24degrees centigrade. Zeinali et al.,³⁶ studied germination in 12wheat varieties and reported their optimum temperatures varied from 31.8 to 32.4, and their ceiling temperatures from 38.1 to 42.1degrees centigrade. Jame et al.,²⁹ showed in their study that the base, optimum and ceiling temperatures for wheat were 0, 30 and 42degrees centigrade, respectively. Khalili³⁰ studied germination in barley and found the base, optimum, and ceiling temperatures were -0.09, 27.5 and 35.7degrees centigrade, respectively.

Our research showed that of the three common non-linear regression models for quantifying the effects of temperature on germination rate in the three varieties of Shomal, Mollasani, and Majarestan (the beta, the dent-like, and the segmented models), the beta model fitted the observed data best. Therefore, it was selected as the superior model and was used in the determination the cardinal temperatures of germination (the base, the optimum, and the base temperatures). Consequently, the beta model and the parameters estimated by it may be utilized in creating and evaluating predictive models of germination. These parameters can be saved in data banks of various varieties to be used in determining their cardinal temperatures of germination. Results of our research indicated that, in the studied varieties, there were no great differences between the curves showing responses to temperature, and this makes us more confident in using the obtained values, coefficients and biological time.

None.

The author declares no conflict of interest.

1. Keville K. The Illustrated Herb Encyclopedia; A Complete Culinary, Cosmetic, Medicinal, and Ornamental Guide to Hers. Simon a Schuster Australia. New South Wales: East Roseville; 1991.
2. Omidbaigi R. Production and Processing of Medicinal Plants. Vol 2, In Farsi: Astan Quds Razavi Publications; 2009. 439 p.
3. Foley ME, Fennimore SA. Genetic basis for seed dormancy. Seed Sci Res. 1998;8(2):173–182.
4. Meyer SE, Pendleton RL. Genetic regulation of seed dormancy in purshia tridentata (Rosaceae). Ann Bot. 2000;85(4):521–529.
5. Windauer L, Altuna A, Arnold RB. Hydrotime analysis of Lesquerella fendleriseed germination responses to priming treatments. Indt Crop Prod. 2007;25(1):70–74.
6. McDonald MB. Seed priming: 287–525. In: Black M, et al. editors. Seed Technology and Its Biological Basis. Shettield, Uk: Sheffield Academic press; 2000. 428 p.
7. Bloomberg M, Sedcole JR, Mason EG, et al. Hydrothermal time germination models for radiata pine (Pinus radiataD. Don). Seed Sci Res. 2009;19(3):171–182.
8. Dubetz S, Russell V, Anderson DT. Effect of soil temperature on seedling emergence. Can J Plant Sci. 1962;42(3):481–487.
9. Heydecker W. Stress and seed germination. An agronomic view In: editor. Khan AA. The physiology and chemistry of seed dormancy and germination. 237–276. North Holland. Oxford. Biomedical Press; 1977.
10. Huidobro JG, Monteith JL, Saquire GR. Time, temperature and germination of pearl millet (Pennisetum typhoidesS. and H.) I. Constant temperature. J Exp Bot. 1982;33(2):288–296.
11. Mwale SS, Azam–Ali SN, Clark JA, et al. Effect of temperature on the germination of sunflower. Seed Sci Technol. 1994;22:565–571.
12. Ramin AA. The influence of temperature on germination taree Irani. Seed Sci Technol. 1997;25(3):419–426.
13. Bewley JD, Black M. Seeds: Physiology of Development and Germination. 2nd ed. New York, London, USA: Plenum Press; 1994.
14. Kamkar B, Ahmadi M, Soltani A, et al. Evaluating non–linear regression models to describe response of wheat emergence rate to temperature. Seed Sci Technol. 2008;2:53–57.
15. Kamkar B, Koocheki AR, Nassiri Mahallati M, et al. Cardinal temperature for germination in three millet species (Panicum miliaceum, Pennisetum glaucumand Setaria italica). Asian J Plant Sci. 2006;5:316–319.
16. Alvarado V, Bradford KJ. A hydrothermal time model explains the cardinal temperatures for seed germination. Plant Cell Environ. 2002;25(8):1061–1069.
17. Phartyal SS, Thapliyal RC, Nayal JS, et al. The influences of tempeloprasum on seed germination rate in Himalayan elm (Ulmus wallichiana). Seed Sci Technol. 2003;31:83–93.
18. Bewley JD. Seed germination and dormancy. Plant Cell. 1997;9(7):1055–1066.
19. Soltani A, Robertson MJ, Torabi B, et al. Modeling seedling emergence in chickpea as influenced by temperature and sowing depth. Agr Forest Meteorol. 2006;138(1–4):156–167.
20. Riemens MM, Scheepens PC, Van der Weide RY. Dormancy, germination and emergence of weed seeds , with emphasis on influence of light. Plant Research International BV. 2004;302:1–2.
21. Al–Ahmadi JM, Kafi M. Cardinal temperatures for germination of Kochia scoparia(L). Journal of Arid Environments. 2007;68(2):308–314.
22. Mahmoodi A, Soltani E, Barani H. Germination response to temperature of snail medic (Medicago scutellataL.). Elect J Crop prod. 2008;1(1):54–63 (In Farsi).
23. Hardegree SP, Winstral AH. Predicting germination response to temperature. II. Three–dimensional regression, statistical gridding and iterative–probit optimization using measured and interpolated–subpopulation Data. Ann Bot. 2006;98(2):403–410.
24. Banayan M. Development and applications of simulation models in agriculture. Iran; Ferdowsi University Press; 2006. 208 p. (in Farsi).
25. Hardegree SP. Predicting germination response to temperature. I. Cardinal temperature models and subpopulation–specific regression. Ann Bot. 2006;97(6):1115–1125.
26. Akram–Ghaderi F. The study of seed quality development, germination, longevity and deterioration in some medicinal plants:medicinal pumpkin (Cucurbita pepo L. subsp. Pepo. Convar:Pepo var. styriaca Gerb), cumin blank (Nigella sativa L.) and borago (Borago officinalis L.). Ph.D. Thesis, Gorgan. Univer. Agric Sci Natur Resour; 2008. 180 p.
27. Soltani E, Ghaderi FA, Soltani A. Applications of germination modeling on the response to temperature and water potential in seed science research. 1st National Conference of Seed Sci and Technology in Iran. Gorgan, Iran. Plenum Press; 2008. 445 p.
28. Kamkar B, Jami Al–Ahmadi M, Mahdavi Damghani A, et al. Quantification of the cardinal temperatures and thermal time requirement of opium poppy (Papaver somniferum L.) seeds to germinate using non–linear regression models. Ind Crop Prod. 2012;35(1):192–198.
29. Jame YW, Cutforth HW. Simulating the effects of temperature and seeding depth on germination and emergence of spring wheat. Agr Forest Meteorol. 2004;124(3–4):207–218.
30. Khalili N. Predicting barley (Hordeum vulgare L.) emergence as affected by temperature, moisture and sowing depth. Gorgan Univer Agric Sci Natur Resour; 2013. 60 p.
31. Ghaderi–Far F, Soltani A, Sadeghipour HR. Evaluation of nonlinear regression models in quantifying germination rate of medicinal pumpkin (Cucurbita pepo L. subsp. Pepo. Convar:Pepo var. styriaca Gerb), borago (Borago officinalis L.) and black cumin (Nigella sativa L.) to temperature. J Agric Sci Nat Resour. 2009;16(4):1–20.
32. Soltani A. Appilication of SAS in statistical analysis. Jihad–daneshgahi; Mashhad, Iran: Press; 2007. 180 p.(In Farsi).
33. Ahmadi M, Kamkar B, Soltani A, et al. Evaluation of non–Linear regression models to predict stem elongation rate of wheat (Tajan cultivar) in response to temperature and Photoperiod. Elect J Crop Prod. 2010;2(4):39–54.
34. Nadjafi F, Tabrizi L, Shabahang J, et al. Cardinal germination temperatures of some medicinal plant species. Seed Sci Technol. 2009;31(2):156–165.
35. Kamaha C, Magure YD. Effect of temperature on germination of six winter wheat cultivars. Seed Sci Technol. 1992;20:181–185.
36. Zeinali E, Soltani A, Galeshi S, et al. Cardinal temperatures, response to temperature and range of thermal tolerance for seed germination in wheat (Triticum aestivum L.) cultivars. Elect J Crop Prod. 2010;3(3):23–42.