Quilt Packaging® (QP) is a new direct, interchip interconnect through metal nodules on chip edges. We have performed simulations to study the robustness of QP against fatigue failure. For quilts on ceramic carriers, thermal stresses are driven primarily by the adhesive between chip and carrier, and we have simulated systems with different adhesives, as well as different chip material combinations. Simulations for the test system estimated cycles-to-failure over a temperature range of -55 to 125°C. The simulation results suggest favorable material properties for solder and adhesive to use for QP or QP-like interconnects.

Keywords: nodule, quilt package, reliability, solder joint, fatigue

Interchip interconnects made of wire bonds and solder bumps often constrain high-speed operation. To improve performance, a novel interconnect method has been developed,^1,2 called Quilt Packaging® (QP),³ implementing a 2D system-in-package (SiP) paradigm. In this technique, two or more chips, not necessarily of the same material, are connected along their edges to form a “quilt” of chips connected by metal nodules that protrude out from the edges of chips to effect a direct, chip-to-chip electrical interconnect, as shown in Figure 1.

Figure 1 Schematic illustration of a Quilt Packaging interface between two chips. The figure shows a chip on the left with idealized metal regions, a chip on the right with interconnects, a gap between the two chips, and two pairs of QP nodules that in this case are patterned with alignment features. Nodule L is embedded in the left chip and nodule R is embedded in the right chip. Shown between the nodules at their interface is a light-colored region representing a thin layer of solder. Image courtesy of Indiana Integrated Circuits, LLC.

In QP, nodules are deposited into the substrate surface, and after a dry etch step for die singulation are left protruding off the edges of the chip. The fabrication process is discussed in.² The nodules are anchored in the substrate material and provide a degree of mechanical rigidity after two chips are brought together at their edges and facing nodules are soldered. Although two chips so quilted are fabricated in separate processes, they function nearly as a single chip due to the almost lossless performance of the QP interconnect. The RF performance of connections has already been investigated, and shown to be capable of extremely high bandwidths.⁴ This makes it possible to separately choose the best material for different functions (e.g., a processor and memory).

QP is subject to thermal reliability issues depending on application, materials, shape, and operating temperature. Due to the continued scaling of CMOS, power density in a chip can be high. Quilted chips, unlike stacked ones, can all be placed on a heat sink, helping to minimize thermal effects. Nevertheless, thermal stress is still an important factor for QP as for any interconnected structure. In this paper, a model for QP is developed. We find that QP is structurally robust, as shown by thermal simulation results.

Introduction to QP reliability

Thermomechanical reliability issues in QP originate from mechanical stress due to different coefficients of thermal expansion (CTE) of the materials used in a bonded quilt. Two kinds of issues arise: a) fracture from stress exceeding material strength and b) fracture from cycling fatigue. We have found previously that sharp corners in the oxide layer cause high stress and make it prone to fractures. Consequently, all models and devices discussed in this paper use beveled lower edges, which were found⁵ to keep the von Mises stress below the ultimate stress in the oxide. This paper deals with the second issue, in particular the fracturing of the solder joint.

Thermal stresses arise in two ways. The primary way is that initially unstressed devices become stressed when temperature changes combined with different CTE’s cause nonuniform expansion or contraction. Second, there is a kind of frozen-in temperature difference: when one material is deposited on a surface and solidifies while still hotter than the surface, upon cooling there will be a residual stress approximately proportional to the deposition temperature difference (this would be the case even for identical CTE’s). For our simulations, we assumed zero residual stress. This is a realistic assumption: our QP fabrication process uses near-room-temperature processes (e.g., electrodeposition of Cu), and in models developed to describe them we have found the residual stresses are small. As a new technology, QP does not yet have an established reliability testing methodology; we therefore borrow from existing reliability standards for ICs.

Structure of QP

We simulated the thermal deformation of components both separately and in quilted pairs using COMSOL version 3.5a. Here, we focus on a 10-nodule-pair quilt. This is a design compromise, since the time and memory requirements for COMSOL to obtain accurate results (i.e., using a fine mesh) for a realistic quilt of many more nodule pairs would be excessive.

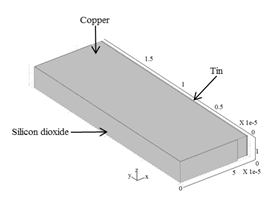
Simulations with smaller numbers of nodules show that the stresses tend to decrease monotonically with increasing numbers of nodules. This implies that practical quilts with considerably more nodules will be more robust than estimated in this paper. (Figure 2) shows a single nodule unit used in the simulations, indicating the regions where it is anchored in the substrate and where it extends out from the side of the chip. The Cu is surrounded by a 0.5 m insulating layer of SiO₂. All oxide layers shown are embedded in the semiconductor; the rest of the nodule protrudes from the substrate, and is used for interconnection. For the model shown in Figure 2, the total length is 70 m, of which 10μm extends beyond the substrate, width is 200 m, depth is 20 m, and the bare Cu is capped by 1 m of electrolessly deposited Sn or Sn-based alloy.

Figure 2 Model of a single simple Cu nodule similar to nodule L of Figure 1, but with flat interface surface at the right. Embedded length, depth, and width are 60, 19 and 199μm. The nodule is partially embedded in a 0.5μm oxide layer to electrically isolate the nodule from the substrate.

Nodules connect adjacent substrates, which may be of the same or different materials. A quilt combining substrates of a single material we call a homogeneous quilt; one combining substrates of different materials we call a heterogeneous quilt. The two chips are attached by epoxy to a common chip carrier. Figure 3 shows a complete quilt, which includes 2 substrates, 10 pairs of nodules, epoxy, and chip carrier. The substrates used in the simulations are Si and GaAs in various combinations, and ceramic is used for the chip carrier. This structure has dimensions 5mm×5mm; the substrate, epoxy and carrier have thicknesses 530, 100 and 500 m, respectively. A 200- m-thick layer of copper on the ceramic is used to spread heat.

Figure 3 COMSOL model of two chips connected along their edges by 10 QP nodules. (a) Two adjacent chips (upper structures) quilted on a layer of epoxy on a chip carrier (bottom layer). Multiple metal nodules along the gap between the two chips effect electrical and mechanical connections. (b) Expanded view of the encircled top part of (a).

Our simulations use three elastic constants (C11, C12, C44)^6–8 to take full account of the anisotropy of single crystal semiconductors. The Cu, oxide, epoxy and ceramic materials are treated as isotropic. For reference purposes, the z direction is the usual “vertical” direction for integrated circuits, the x direction is the direction from one chip to the other through the gap, and the y direction is the direction along the quilt, parallel to the quilted edges.

Location of stress maxima

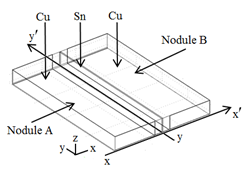
In order to determine the stresses that cause fatigue, it is necessary to model the full 6-component stress tensor (3 normal and 3 shear components) over the entire quilted system including the nodules, solder, oxide, bulk semiconductor, adhesive, and ceramic substrate. The highest stresses, as previous studies have shown, occur in the oxide, which is not subject to fatigue. We focus our attention on the stress in the nodule pairs because they are subject to fatigue. Fatigue failure in general is known to depend in different ways on the stress tensor. In ball-grid array (BGA) and many other current packaging technologies, fatigue failure occurs primarily as a result of shear stress. One of the distinguishing features of QP is that fatigue arises from normal stresses. The stress relevant to our study is _x– the normal stress along the direction from one nodule to the other in a pair. For the remainder of the paper, “stress” will implicitly mean _x (likewise “strain” is _x).

In fatigue studies, we are concerned with the location of the maximum stress because that is where failure begins. Within each nodule pair, the maximum stress occurs in a narrow range of x corresponding to the Sn layer Figure 4. Within the Sn layer the stress varies substantially, with maximum stress at the edges and minimum at the centers. The maximum occurs at the lower outer corners, indicated by the intersection of lines x-x’ and y-y’ in Figure 4. Simulations found that among different nodule pairs, the stress patterns are similar but slightly offset, with the highest stresses occurring in the center nodules, and decreasing by about 10% as one moves along the quilt edge to the outer nodule pairs.

Figure 4 Maximum stress in bonded nodule pair occurs in the Sn at the intersection of lines x-x and y-y.

Effect of adhesive properties on stress

After two chips are connected by electroless Sn or Sn-based alloy, an adhesive is used to attach the chips to the copper that is layered onto the ceramic chip carrier. We performed simulations using 3 different epoxies chosen to have a range of CTE values, and one die adhesive film. The properties are shown in Table 1.

The strain in the Sn reaches values much greater than the limit of elastic strain. In a ductile material like Sn, the nonlinear strain is determined in a standard way by distinguishing “true” strain and “engineering” strain.⁸ The elastic component of the strain relaxes essentially linearly, allowing the plastic strain p to be calculated.

Plastic strain is the result of a process of inelastic deformation, so unlike elastic strain, which depends only on the current temperature, the plastic strain depends at least on the current temperature and on the initial temperature before plastic deformation. Strain can also arise from temperature inhomogeneities, but the time scale for thermal cycling is expected to be much longer than the time scale of thermal equilibration, so the temperature distribution is taken to be uniform at any given moment during the cycle of overall temperature variation. Table 2 shows how plastic strain depends on the number of nodules, using 6, 8, and 10 nodule pairs in the model of Figure 3. The results are based on a Si-Si quilt using a 100 m thick, 20ppm/°C CTE epoxy, with the plastic strain produced by heating from 20°C to 125°C. As one would expect, increasing the number of nodules reduces strain, since the stress is shared by more nodules.

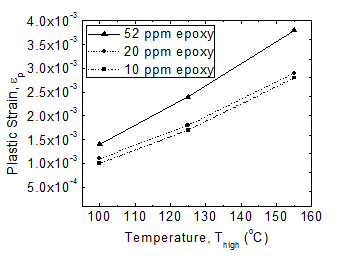
Table 3 shows the effect of epoxy thickness for the same Si-Si quilt and 20ppm/°C CTE epoxy, for 10 nodule pairs. With a reference temperature of 20°C, strain was produced by heating to 125°C. The epoxy thickness was varied from 20 to 200 m. (Figure 5) shows the plastic strain in Sn for homogeneous quilts using various epoxies, all 100 m thick. The plastic strain is computed for an entire thermal cycle: starting at the reference temperature of 20°C, heating to a high temperature (indicated on horizontal axis of the graph), cooling to a low of 0°C, and returning to the reference temperature. The plastic strain in this case has two contributions-a tensile plastic strain from the hot stage, and a compressive plastic strain from the cold part of the cycle. (Figure 6) shows the effect of changing the lower end of the temperature excursion, with different curves representing T low values of 0°C and 55°C (these choices correspond to two common experimental standards).^9,10 Qualitatively, as expected, a larger temperature excursion increases plastic strain. It is instructive to compare the total plastic strain for the 0 to 155°C cycle and the 55 to 100°C cycle. Both are excursions with total range 155°C, but the higher-temperature excursion has a greater plastic strain (4.25E 3 vs 3.75E 3). Moreover, the material parameters in our model are temperature-independent, so a simple temperature shift does not cause different ranges of material-parameter values to be explored. The reason for the difference is the nonlinearity of plastic strain. In the lower-temperature cycle, the high and low temperatures differ by 80°C and 75°C from the reference temperature. The higher-temperature cycle consists of upper and lower excursions by 135°C and 20°C away from reference.

Figure 5 Plastic strain in Sn for homogeneous quilts with epoxies EP30HT, EP21TCHT1, and epoxy;⁸ thickness is 100μm, and T_low=0°C.

Figure 6 Plastic strain in Sn for 10-μm thick QMI5100 adhesive film in a Si-Si quilt.

The choice of semiconductors is also important, of course. Figure 7 shows the plastic strain for a complete cycle from a common T low of 0°C to high temperatures indicated on the horizontal axis. The general trend is that replacing Si with GaAs results in decreased plastic strain, so the thermal expansion of the semiconductor appears to reduce the strain in the nodules.

The heterogeneous (GaAs-Si) quilt has plastic strains that fall very close to the averages of those of the homogeneous (Ga and Si) quilts. One might expect a higher plastic strain: the different CTE’s on the two sides of the quilt edge should lead to a lateral (y-direction) shearing of the nodules. This may be an effect in very large quilts, but it is not likely to be important normally because the mismatch is between different but low values of semiconductor CTE. As noted, in QP-unlike BGA-it is the normal rather than shear components of stress that matter most.

Figure 7 Plastic strain in Sn for 20μm thick QMI5100 adhesive. The strain is higher for low CTE Si than for GaAs; T_low=0°C.

Ultimately, what we want from a fatigue analysis is an estimate of time-to-failure. A common approach is to use the Coffin-Manson (C-M) relation to calculate number of cycles to failure (fatigue lifetime). For low cycle fatigue, the C-M relation is

$\Delta \epsilon -pN\_f^{\wedge }\alpha =\theta$(1)

where [$\Delta \epsilon$ ]_p, N_f,$\alpha$ and $\theta$ are plastic strain range, fatigue lifetime, fatigue ductility exponent, and fatigue ductility coefficient, respectively. Using $\epsilon$ _p calculated as previously (Sec. II.D), we determined N_f for various Sn-based alloy solders.

We estimate failure lifetimes for homogeneous Si QP structures with 10 nodule pairs for three Sn-based solders: Sn-37 mass % Pb, Sn-3.5 mass % Ag and Sn-0.7 mass % Cu. The material parameters used are shown in Table 4. We extracted the fatigue parameters ($\alpha$ and $\theta$ \), shown in Table 5, by curve fitting the data presented in.11 (The data of11 were obtained using a strain rate of 0.1% s1).

The simulations show failure lifetime for adhesive film QMI5100 and 10ppm/°C epoxy. The temperature cycles simulated were 0°C to 155°C and -55°C to 155°C. Figures 8–10 show failure lifetime for the film, which has a thickness of 10 m and a CTE of 76ppm/°C. Figures 11–13 show lifetime for the epoxy (100 m, 10ppm/°C).

(Figures 8–10) are for Sn-37Pb, Sn-3.5Ag, and Sn-0.7Cu, resp. From the three figures, it is evident that the solders Sn-37Pb and Sn-0.7Cu are more vulnerable to thermal cycling than the lead free Sn-3.5Ag. This is also the case with 10ppm/°C epoxy, shown in Figures 11–13. It is evident, moreover, that for each solder, the 10ppm/°C epoxy outperforms the adhesive film.

Figure 8 Failure cycles for Sn-37 Pb solder in a 10-nodule-pair quilt with adhesive film QMI5100.

Figure 9 Failure cycles for Sn-3.5Ag solder in QP structure with adhesive film QMI5100.

Figure 10 Failure cycles for Sn-0.7Cu solder in QP structure with adhesive film QMI5100.

Figure 11 Failure cycles for Sn-37 Pb solder in a 10-nodule-pair quilt with epoxy.

Figure 12 Failure cycles for Sn-3.5Ag solder in QP structure with epoxy.

Figure 13 Failure cycles for Sn-0.7Cu solder in QP structure with epoxy.

In this paper we study some aspects of reliability issues in QP, particularly low-cycle fatigue failure in the solder. We focused on the solder because it is the component most vulnerable to fatigue. and computed the plastic strain from thermal cycling. We developed an FEA model of QP and used the model to compute plastic strain, then used this in the Coffin-Manson equation to estimate the fatigue lifetime.

The plastic strain was computed for both homogeneous (Si-Si, and GaAs-GaAs) and heterogeneous (GaAs-Si) quilts. For our 5mm chips, the stress is less sensitive to the choice of semiconductor than to the choice of epoxy, as the semiconductors all have low CTEs, while the epoxies have a broad range of CTEs. The results of the plastic strain, derived from (Table 1 & Figure 5), show that the selection of epoxies is critical in reducing stress in the nodule and they also indicate that the product of CTE and Young’s modulus of the epoxies is an important factor for the produced thermal stress for the temperature range considered .

Increasing the number of nodules substantially reduces the strain in the solder. Any electrically disconnected nodules in QP still serve to extend the fatigue lifetime, i.e., cycles to failure. Thicker epoxy between the bottom of the chips and the copper of the chip carrier reduces strain in the solder. With Sn 3.5Ag solder and 100 m-thick 10ppm/°C epoxy, fatigue lifetimes are in the range of 104. Even without further optimization of adhesive thickness and solder choice, this demonstrates that QP is a practical interconnection option. The fatigue ductility exponent, compared to fatigue ductility constant, plays a critical role in determining the life cycle of the solder; a smaller ductility exponent increases the life cycle of the contact significantly-evident from (Table 5 & Figures 8-10). For QP or QP-like structures, these parameters-E and CTE of the epoxy, and fatigue parameters of the solder-are, therefore, needed to be considered when optimum reliability of the interconnect is a concern.

This work was supported by Rockwell Collins Inc., Sandia National Laboratory, Department of Defense, and the National Science Foundation under award ECS-0636575. We thank G Snider, P Fay, and D Kopp for helpful discussions and E Bensman for assistance with COMSOL.

The authors declared no potential conflict of interest with respect to the research, authorship, and/or publication of this article.

1. Bernstein GH, Liu Q, Yan M, et al. Quilt Packaging: High–Density, High–Speed Interchip Communications. IEEE Transactions on Advanced Packaging. 2007;30(4):731–740.
2. Liu Q, Fay P, Bernstein GH. A Novel Scheme for Wide Bandwidth Chip–to–Chip Communications. International Microelectronics and Packaging Society. 2007. 4(1).
3. Quilt Packaging is a trademark of Indiana Integrated Circuits, LLC.
4. Patrick Fay, Gary H Bernstein, Tian Lu, et al. Ultra–wide Bandwidth Inter–Chip Interconnects for Heterogeneous Millimeter–Wave and THz Circuits. Journal of Infrared, Millimeter, and Terahertz Waves. 2016;37(9):874–880.
5. Khan MA, Kriman AM, Bernstein GH. Thermal Modeling of Quilt Packaging Interconnects. Micro/Nano Symposium (UGIM), 2010 18th Biennial University/Government/Industry. 2010.
6. Muramatsu S. Simple expression for elastic constants c11, c12 and c44 and internal displacements of semiconductors. Journal of Applied Physics. 1993;73(9):4270–4272.
7. Pradeep Lall, Milan Shah, Luke Drake, et al. Thermo–mechanical reliability management models for area–array packages on Cu–core and no core assemblies. SMTA Journal. 2008;21(3):20–35.
8. Courtney TH. Mechanical Behavior of Materials, McGraw–Hill, 1990. JESD22–A104D, JEDEC Solid State Technology Association. Temperature Cycling. 2009:5.
9. IPC–9701A. Performance Test Methods and Qualification Requirements for surface Mount Solder Attachments. A standard developed by IPC, IPC–9701A. 2006. 8 p.
10. Takahashi T, Hioki S, Shohji I, et al. Fatigue Damage Evaluation by Surface Feature for Sn–3.5Ag and Sn–0.7Cu Solders. Materials Transactions. 2005;46(11):2335–2343.
11. Warner M, et al. Flo/Stress: An Integrated Stress Solver for The Cfd Tool Flotherm. Proceedings of IPACK'01: The Pacific Rim/ASME International Electronic Packaging Technical Conference and Exhibition. 2001. p. 8–13.
12. Schubert A, Walter H, Dudek R, et al. Thermo–Mechanical Properties and Creep Deformation of Lead–Containing and Lead–Free Solders. International Symposium on Advanced Packaging Materials. 2001.
13. Asahi Solder. IPC version 3. 2007.