In this work, The Equilibrium Molecular Dynamics (EMD) is applied for computing the thermal conductivity of aqueous nanofluids containing graphene nanosheets (aqueous GNFs), through Green-Kubo framework and studying the effects of concentration and temperature on thermal conductivity enhancement of aqueous GNFs. The SPC/E water model was chosen and the interactions for water molecules have been modelled by the Lennard-Jones (L-J) potential combined with Coulomb potential, as well as a simple body (L-J) potential is used to model the interactions between graphene atoms. The numerical calculations of thermal conductivity are performed in the temperature range of 293–343K and for graphene nanosheets volume fraction 0.175%, 0.190%, 0.306%, 0.521% and 0.722%. Firstly, the molecular dynamics code and the Green-Kubo framework are validated by comparing the thermal conductivity with the previous experimental studies. The results have showed that the thermal conductivity enhancement increases with increasing volume concentration and is substantial even at lower concentrations. However, this enhancement has been not predicted by the classical Maxwell’s model. Furthermore, the enhancement depends on temperature, especially, the thermal conductivity of aqueous nanofluids containing graphene nanosheets (aqueous GNFs) increases with increasing system temperature.

Keywords: aqueous nanofluids, thermal conductivity, molecular dynamics simulations, water, graphene nanosheets

The nanofluid is a fluid containing nanometer-sized particles, with sizes typically in the order of 1-100nm, which are called nanoparticles (NPs).¹ This new class of fluids could be created by the addition of nanoparticles in the base fluid.¹ Furthermore, the nanoparticles used in nanofluids are typically made of metals, oxides, carbides, or Carbon nanotubes (CNTs), they are useful in enhancing fluid’s properties,^2–4 this alteration is caused by the hybrid composition of fluid and NPs. The base fluids include many kinds of liquids such as, water, ethylene glycol, and oil. Several research projects of the late 1990s and the first decade of the twenty-first century indicated that the addition of very small amounts of nanoparticles in commonly used base fluids increases significantly the effective thermal conductivity of these mixtures. Masuda et al.⁵ reported that with low nanoparticles concentrations (1–5Vol %), the effective thermal conductivity of the suspensions increases more than 20%. As well as, Choi et al. (2001).⁶ measured the thermal conductivity of suspension multi-walled CNTs in engine oil, they reported that the thermal conductivity of the base fluid growth more than doubled even at the very low concentrations of multi-walled CNTs in engine oil. Yulong Ding et al.⁷ also studied experimentally the heat transfer behaviour of aqueous suspensions of multi-walled carbon nanotubes (CNT nanofluids), they also observed very high enhancement of the effective thermal conductivity, furthermore, viscosity and convective heat transfer coefficient, close to 350%, for nanofluids containing 0.5% CNTs. In addition, Huaqing Xie et al.⁸ proposed a method to produce stable and homogeneous suspensions of CNTs in distilled water (DW), Ethylene glycol (EG), and decene (DE) and report enhanced thermal conductivities of these nanofluids.

Another, several studies are carried on graphene– water nanofluid. Nizar Ahammed et al.⁹ measured the thermal conductivity of graphene–water nanofluid at below and above ambient temperature, they reported that the thermal conductivity increases with increasing the volume concentrations of graphene, and its enhancement is close the 37.2% for 0.15% volume concentration of graphene at 50°C when compared with that of the water at the same temperature. C. Selvam et al.¹⁰ prepared the ethylene glycol and water based graphene fluids with deoxy cholate surfactant and measured their thermal conductivities; they observed that the thermal conductivity enhancement of graphene nanofluid significantly increases with increasing particle volume fraction and decreases with increasing base fluid thermal conductivity. Hossein Akhavan-Zanjani et al.¹¹ investigated experimentally the transport coefficients of nanofluids aqueous nanofluids containing graphene nanosheets, they reported that the thermal conductivity enhances considerably. Therefore, a number of physical mechanisms have been proposed to explain the thermal conductivity enhancement of a nanofluid. One of the mechanisms, Ya et al.,¹² Leong et al.¹³ & keblinski et al.¹⁴ proposed that the interfacial layering or formation of a solid-like, which has a much higher thermal conductivity than the bulk liquid itself, was the main parameter affecting the thermal conductivity enhancement of nanofluid. This effect was later proved to be nominal.¹⁵ As well as, Chon et al.¹⁶ measured the thermal conductivity in the temperature range of 20–70°C. They reported that the increasing of the Brownian motion and the micro-convection are the main factors for thermal conductivity enhancement of nanofluids. The study was carried by Timofeev et al.¹⁷ that measured thermal conductivity enhancement and nanoparticle sizes; they concluded that the enhancement thermal conductivity of the suspension is significantly affected by the formation of particle clusters and aggregates.

Due to their novel properties, the nanofluids are used in various fluidic applications including heat transfer such as microelectronics, fuel cells, pharmaceutical processes, and hybrid-powered engine,^15,18–19 tribology,²⁰ lubrication,²¹ chemical mechanical planarization.²² Experimentally, nanofluids were studied by diverse experimental procedures, which were expensive, as well as carrying out easy experimentation required high level of material and equipment usage. Furthermore, a major of experimental studies have been performed on the transport properties of nanofluids. Numerically several methods have been applied for calculating the thermal conductivity of nanofluids, nanoparticles and bulk materials, one of the main of these methods is the equilibrium molecular dynamics combined with Green-Kubo method, for example the determination of nanofluid (Ar-Cu) thermal conductivity, and its reliance on temperature and volume fraction,^23–24 as well as, Equilibrium Molecular Dynamics (EMD) through Green-Kubo formula and Einstein relation, and the Nonequilibrium Molecular Dynamics (NEMD) using Einstein–Smoluchowski relation methods, are developed to calculate the rotational diffusion coefficient of a carbon nanotube in fluid,²⁴ Viscosity and diffusion coefficient of nanofluid (CuO–water) were calculated by Equilibrium Molecular Dynamics (EMD) with the help of Green–Kubo formula.²⁵ In this present work, the Equilibrium Molecular Dynamics (EMD) integrated with Green-Kubo method is used systematically to calculate the thermal conductivity of aqueous graphene Nanosheet nanofluids and investigate the effects of temperature and volume fraction. The effect of temperature is studied by analysing the temperature reliance of the kinetic energy and the microscopic heat flux. Also, the effect of volume fraction is studied by analysing the volume fraction dependence of the potential energy and the microscopic heat flux. The results show that increasing system temperature enhances the system thermal conductivity significantly. Also, the increasing of volume fraction causes an increase in thermal conductivity enhancement.

Equilibrium Molecular dynamics (EMD) is the numerical integration of the classical equations of motion for a system of interacting atoms over a certain period of time. In classical molecular dynamics, the force acting on an atom can be calculated from the muddling of its inter-atomic potentials with its neighbours, by applying the Newton’s second law.²⁶ As a result, the interaction forces between atoms, the kinetic and potential energies of atoms are calculated at each time step, from inter-atomic potentials between all atoms of system. In general, an accurate simulation of the nanofluid takes all possible atomic interaction in system. Therefore, to simulate the aqueous graphene Nanosheet nanofluids, the Lennard-Jones (L-J) potential is used to model the carbon-carbon interaction,²⁷ is defined by

$U(r_{ij})=4{\epsilon }_{ij}\left[{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^{12}-{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^6\right]$ (1)

Where e_ij is the depth of the potential well, s_ij is the finite distance at which the pairwise potential is zero, their values are listed in Table 1, and r_ij is the distance between atoms i and j. The SPC/E (extended simple point charge) model,²⁸ is used to describe water molecules interactions, its force field parameters are listed in Table 2. This model SPC/E can be described as effective rigid pair potentials composed of Lennard-Jones (L-J) and coulombic terms^29–31 is given as fellow

$U(r_{ij})=4{\epsilon }_{ij}\left[{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^{12}-{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^6\right]+\frac{q_i{q}_j}{r_{ij}}$ (2)

Where q_i is the partial charge of atom i, the values of parameters that correspond to the expression in equation (2) are shown in Table 1. Furthermore, the potential Lennard-Jones (L-J) used for modelling the interaction between atoms of graphene Nanosheet and liquid water is given by equation (1), the values of its parameters are listed in Table 1. The particle–particle particle–mesh (PPPM) technique was used to compute the long-range coulombic forces and the SHAKE algorithm was applied to keep the water molecules rigid.^32,33

The microscopic heat flux and thermal conductivity

In the macroscopic scale, the thermal conductivity is defined as a linear coefficient relating the macroscopic heat flux  to the temperature gradient (Fourier’s law), it is expressed as below.

$\overrightarrow{J}=-k.\overrightarrow{grad}(T)$ (3)

But, in the microscopic scale the thermal conductivity is as a result of the nanofluid interactions, which are carried out nanofluid at the molecular level. Therefore, it is necessary to have a simulation technique which takes the interactions occurring at atomic level for calculating the thermal conductivity of nanofluids. Another, the molecular dynamics simulation an atomic scale simulation technique has been proven to predict the static and dynamic properties of nanofluids. It appears that the equilibrium molecular dynamics combined with Green Kubo formula is the only approach for calculating and explaining the thermal conductivity enhancement of nanofluids at atomic level, in which the thermal conductivity is computed according to equation (4). ^23,34–36

$K_B$ (4)

The parameters $V$ , $T$ , $K_B$ and $\overrightarrow{J}$ are respectively the volume, the temperature, the Boltzmann constant and the microscopic heat flux vector, the last parameter is defined as fellow.

$h_k$ (5)

Where $E_i-\langle E_i\rangle$ refers to the excess of total energy Ei , and ri is the position of atom i. Taking the time derivative of equation (5) gives the following result for the microscopic heat flux.³⁷

$\overrightarrow{j}=\frac{1}{2}{\displaystyle \sum _{k=\alpha }{\displaystyle \sum _{i=1}^{N_{\alpha }}{m}_i^k{\left(v_i^k\right)}^2\overrightarrow{.v_i^k}}}+{\displaystyle \sum _{k=\alpha }{\displaystyle \sum _{l=\alpha }{\displaystyle \sum _{i=1}^{N_{\alpha }}{\displaystyle \sum _{j>i}^{N_l}\left[u(r_{ij}^{kj})+r_{ij}^{kj}.F_{ij}^{kl}\right]}}}}.\overrightarrow{v_i^k}-{\displaystyle \sum _{k=\alpha }{h}^k{\displaystyle \sum _{i=l}^{N_k}\overrightarrow{v_i^k}}}$ (6)

V_i^k indicates the velocity of atoms i of kind k, hk indicates the average enthalpy of species k, Nk is the number of atoms of kind k, the parameters $r_{ij}^{kl}$ , $u(r_{ij}^{kj})$ and $F_{ij}^{kl}$ are the distance, the interaction potential and interacting force between two atoms i of kind k and atoms j of kind l, respectively. The mean partial enthalpy $h_k$ is always zero for single component system. However, it is not zero for multi-component system, and can be computed as the sum of the mean kinetic and potential energies, and the virial.³⁸ Therefore, the mean partial enthalpy of species α can be calculated as equation (7).

$h^{\alpha }=\langle {\displaystyle \sum _{k=1}^{N_{\alpha }}\frac{1}{2}{m}_k{v}_k^2}\rangle +\langle \frac{1}{2}{\displaystyle \sum _{k\ne j}^{N_{\alpha }}u(r_{jk})}\rangle +\langle \frac{1}{2}{\displaystyle \sum _{k\ne j}^{N_{\alpha }}{r}_{jk}.F(r_{jk})}\rangle$ (7)

Where $F(r_{jk})$ is the interaction force between atom i and k of kind α

The microscopic heat flux vector is the addition of three terms, ${\overrightarrow{j}}^K$ , ${\overrightarrow{j}}^P$ and ${\overrightarrow{j}}^C$ that are created by the kinetic, potential and collision energy respectively. However, the partial enthalpy flux doesn’t contribute to the heat flux.³⁴ Thus, the heat flux can be written as

$\overrightarrow{j}={\overrightarrow{j}}^K+{\overrightarrow{j}}^P+{\overrightarrow{j}}^C$ (8)

The three heat flux are defined as bellow.

${\overrightarrow{j}}^K=\frac{1}{2}{\displaystyle \sum _{k=\alpha }{\displaystyle \sum _{i=1}^{N_{\alpha }}{m}_i^k{\left(v_i^k\right)}^2\overrightarrow{.v_i^k}}}$ (9)

${\overrightarrow{j}}^P={\displaystyle \sum _{k=\alpha }{\displaystyle \sum _{l=\alpha }{\displaystyle \sum _{i=1}^{N_{\alpha }}{\displaystyle \sum _{j>i}^{N_l}u(r_{ij}^{kj})}}}}.\overrightarrow{v_i^k}$ (10)

${\overrightarrow{j}}^C={\displaystyle \sum _{k=\alpha }{\displaystyle \sum _{l=\alpha }{\displaystyle \sum _{i=1}^{N_{\alpha }}{\displaystyle \sum _{j>i}^{N_l}{r}_{ij}^{kj}.F_{ij}^{kl}}}}}.\overrightarrow{v_i^k}$ (11)

${\overrightarrow{j}}^K$ and ${\overrightarrow{j}}^P$ represent the energy transported across an imaginary plane. The heat flux ${\overrightarrow{j}}^C$ originates from the work done by the virial or the shear stress tensor which results from collision between the constituent atoms.

Bulk water

The molecular dynamics simulations of bulk water were carried out using the SPC/E water model, its parameters are presented in Table 1 & Table 2. Water molecules were initialized in a simple cubic lattice for preventing the overlapping in a random placement of molecules as shown in Figure 1, the size of box of molecules of pure water was related to the number of molecules in box, 1000 molecules of water was chosen to achieve the density of about 950kg/m³. As well as, periodic boundary condition (PBC) is realised in three dimensional of the simulation system of pure water, it permits the modelling of very large system. Also, the particle–particle particle–mesh (PPPM) technique was used to compute the long-range coulombic forces and the SHAKE algorithm was applied to keep the water molecules.³² A cut-off radius at 9Å is used for the Lennard-Jones pair-style with long-range coulomb interactions. The simulation was executed for calculating the thermal conductivity of pure water for various system temperatures ranging from 293 to 343K at pressure 1atm. A time step of 2fs was used in all simulations. The system was equilibrated in the NVT ensemble for 2.5´10⁵ steps and the system temperature was maintained by using the Berendsen thermostat. After the equilibration period, the temperature constraint was removed and the system was allowed to evolve in the NVE ensemble for 1´10⁶ steps. Furthermore, in this period the position, the velocity and force of each atom are calculated at each time step. Next, all other properties of the system kinetic energy, potential energy, temperature are calculated from the velocity and position of each atom. The data provided by the programme of molecular dynamics is used for computing the total energy and the thermal conductivity of pure water. In this situation, the thermal conductivity was computed by the discretization of the right-hand side of the equation (4) in Δt time steps as following,^23,37

$k=\frac{\Delta t}{3V{k}_B{T}^2}{\displaystyle \sum _{m=1}^M\frac{1}{\left(N-m\right)}{\displaystyle \sum _{n=1}^{N-m}\overrightarrow{j}\left(n+m\right)}}\overrightarrow{j}(n)$ (12)

The parameters $\overrightarrow{j}\left(m+n\right)$ is the microscopic heat at step m+n of molecular dynamics simulation and N is the number total of steps after equilibration system and M is the number of steps in which the time average is computed. The LAMMPS software,³⁹ is used for conducting the molecular dynamics simulations. As well as the visualizing and manipulating data provided by LAMMPS software is realised by using the Open Visualization Tool (OVITO)⁴⁰ and visual molecular dynamics (VMD).⁴¹

Figure 1 Initial system configuration for a 1000 molecules of water, is visualised by OVITO.⁴⁰

Graphene nanofluid

In this work, a nanofluid system consisting of single nanosheet of graphene surrounding by water molecules, were placed in a simple cubic arrangement around de nanosheet (Figure 2). The nanosheet graphene is the carbon nano-layer where the carbon atoms are arranged in hexagonal pattern (Figure 3). The interatomic distance between the adjacent carbon atoms is 1.42Å, and the associated atomistic interaction is covalently bonded by sp2 hybridized electrons.⁴² As well as, the SPC/E water model was chosen in the nanofluid simulations for various volumes fraction 0.175%, 0.190%, 0.306%, 0.521% and 0.722%, in temperature range of 283K≤T≤343K. The periodic boundary condition(PBC) is realised in three dimensional of the simulation system aqueous nanofluids containing graphene nanosheets (aqueous GNFs). A cut-off radius at 9Å is used for the Lennard-Jones pair-style with long-range coulomb interactions, and a time step of 0.1fs was used in all cases of simulation. Also, the simulation domain size was varied proportionally with number of water molecules to maintain a density of 950 kg/m³. In this part, the molecular dynamics simulations were conducted according to the previous procedures used in the simulation of water bulk.

Figure 2 The initial configuration of one nanosheet in water-based nanofluids at 0.175 % volume concentration is visualised by OVITO.

Figure 3 The initial configuration of nanosheet graphene contenting 136 atoms of carbon is visualised by VMD.

Thermal conductivity of pure water

Initially, the internal energy and the thermal conductivity of pure water is calculated for temperatures ranging from 283 to 345K to validate molecular dynamics simulation code, using the Green-Kubo formula for thermal conductivity and the SPC/E (extended simple point charge) water model. The Figure 4 shows the internal energy evolution of pure water inside in simulation domain, during the relaxation at temperatures 293, 303 and 333K. It is observed that after 50ps the internal energy of simulation system of pure water is close to the stability. Therefore, the system is in equilibrium state after 50ps the relaxation. Thus, the subsequent results after 50ps are able to be used for analysis. The Figure 5 shows the variation of thermal conductivity of pure water at various temperatures which range in $283\le T\le 345K$ , it is observed from this figure that the thermal conductivity of pure water increases with the increase in temperature, and it varies between 0.5699 and 0.64589(w/K.m). Consequently, the thermal conductivity of pure water depends on temperature. Since, increasing the temperature induced the collision between pure water molecules due to random motion of molecules. As a result, these collisions physically represent the thermal conductivity of pure water.⁴³ For validating the accuracy and performance of this simulation’s technique and SPC/E model of pure water, same thermal conductivity values of pure water were compared with the existing values measured experimentally.⁴⁴ The Figure 6 shows the comparison between the results obtained from the simulation technique MD through Green-Kubo formula, and the experimental measurements. From the experimental and numerical values of thermal conductivity that are depicted in Figure 6, it can easily be understood that the measured thermal conductivities of distilled water are very close to the experimental data with a maximum uncertainty is 4% at 298K. Hence, the present results validate our simulation of thermal conductivity for pure water. As a result, this study was extended to calculate the thermal conductivity of the nanofluid system with water as the base fluid.

Figure 4 The evolution of internal energy of pure water during MD simulation.

Figure 5 Variation of thermal conductivity of water in the temperature range of 283–345K..

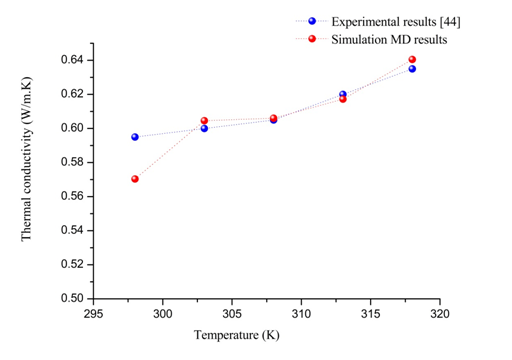
Figure 6 Comparison between the numerical values of thermal conductivity of pure water and the experimental⁴⁴ at various temperatures.

Thermal conductivity of aqueous graphene nanosheet nanofluids

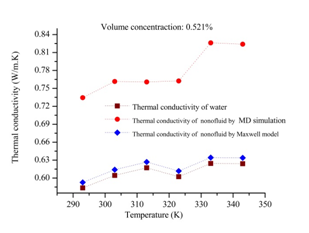
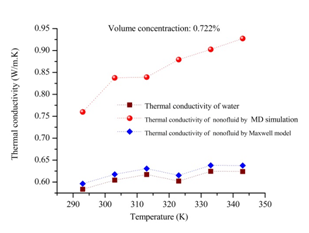
In this part, firstly the internal energy of aqueous nanofluids containing graphene nanosheet (aqueous GNFs) is calculated for volume concentration 0.190% at different temperatures ranging from 293 to 343K. The Figure 7 shows the evolution of internal energy during simulation of nanofluid. It could be found in this figure that after 10 ps the simulation system is in equilibrium state after relaxation, therefore the subsequent results after 10 ps is able to be used for calculating the macroscopic properties of nanofluids such as transport coefficients (thermal conductivity, viscosity, coefficient diffusion). As well as, it is observed that the internal energy of the aqueous GNFs increases with increasing the system temperature. This strong temperature dependence on internal energy of nanofluids is because of the enhanced of solid and liquid atoms at molecular level due to the increasing the system temperature. The thermal conductivity values calculated by our molecular dynamics for aqueous nanofluids containing graphene nanosheets (aqueous GNFs) with 0.190% volume fraction, that are showed in Figure 8 and is compared with the values measured experimentally by Xing Li et al.⁴⁵ They reported that the thermal conductivity of the aqueous GNFs is linearly increased with nanofluid temperature. It is observed that the trend is almost similar for the predicted values by simulation MD and that measured experimentally by Xing Li et al.,⁴⁵ the thermal conductivity which enhances with increase in temperature. The small discrepancies between both values experimental and numerical could be originated from the surfactants used for stabilizing the nanofluid during the experiments. Furthermore, in the experiments other possible factors could be the reason of these deviations, such as the defects in the graphene nanosheets resulted from the strong oxidization of graphite and the incomplete reduction of the oxygen-containing functional groups in the reduced graphene. But these factors aren’t taken into account when the thermal conductivity is calculated numerically. Figure 9 depicts the variation of thermal conductivity of aqueous GNFs as a function of temperature which ranges in $292\le T\le 343K$ for different volume concentration that are 0.175%, 0.190%, 0.306%, 0.521% and 0.722%. It is observed from Figure 9 that increasing system temperature enhances the thermal conductivity significantly of graphene–water nanofluid. This enhancement can be explained by the atomic dynamics combined with the Green– Kubo formula, in which the transport coefficients are calculated from equilibrium molecular dynamics (EMD), via the fluctuation dissipation theorem. In the Green– Kubo approach, the thermal conductivity is computed as the time integral of the microscopic heat flux autocorrelation function $\langle \overrightarrow{j}\left(t\right).\overrightarrow{j}\left(0\right)\rangle$ . In addition, the microscopic heat flux is a addition of three modes equation (8), the flux carried by the kinetic energy ${\overrightarrow{j}}^K$ equation(9), flux carried by the potential energy ${\overrightarrow{j}}^P$ equation (10) and the flux carried by the collisions or the work done by the stress tensor ${\overrightarrow{j}}^C$ equation(11). At high system temperature, the velocities of particles are increasing and by the way the kinetic energy increases as showing in the Figure 10, where the kinetic energy of nanofluid increases with increasing the system temperature. Therefore, the increasing of system temperature leads to increase the flux ${\overrightarrow{j}}^K$ carried by the kinetic energy, in microscopic heat flux equation (8). Thus, the microscopic heat flux is increased, consequently based on equation (4), the thermal conductivity of aqueous GNFs increases with increasing the system temperature. Figure 11 shows the thermal conductivity values which are calculated numerically by molecular dynamics simulation through the Green-Kubo formula, and are compared with that predicted by Maxwell's effective medium theory,⁴⁶ which is given as bellow.

$\frac{k_{nf}}{k_f}=\frac{k_p+2k_f-2\phi \left(k_f-k_p\right)}{k_p+2k_f+\phi \left(k_f-k_p\right)}$ (12)

The parameters k is thermal conductivity and ϕ is particle volume fraction, as well as the subscripts nf, p and f, respectively represent the nanofluid, nanoparticle and base fluid.In the system static in which the Maxwell model is based, the particles are supposed to be in a stationary state and non-interacting. The effective medium theory predicts the thermal conductivity of aqueous nanofluids containing graphene nanosheets with the thermal conductivity of a single-layer grapheme,⁴⁷ $(k_p\approx 3000\text{ W/K}\text{.m)}$ . It is observed from Figure 11 that the enhancement of thermal conductivity calculated numerically increases proportionally with temperature. However, the enhancement of the thermal conductivity predicted theoretically from Maxwell's effective medium theory isn’t influenced by the temperature variations. Generally, the augmentation is significantly negligible than the prediction with molecular dynamics simulation. Hence, the Maxwell's effective medium theory cannot predict the enhancement in thermal conductivity of nanofluids compared with the experimental data that shown in Figure 8.⁴⁵ Since, it does not include the effect of nanoparticle’s size and system temperature, which have been explored to enhance the thermal conductivity of nanofluids. Particularly, it does not take into account various important parameters affecting the heat transport in the nanofluids that is occurred at Nano-scale which is causing the thermal conductivity enhancement. Nevertheless, the molecular dynamics simulation integrated with Green-Kubo method could be an appropriate method to calculate thermal conductivity and study the effect of system temperature on thermal conductivity enhancement at atomic size length scales. Figure 12 shows the variation of the percentage enhancement of the thermal conductivity of graphene–water nanofluid as a function of volume concentration for various temperatures 293, 303 and 323K. It is observed that the enhancement of thermal conductivity increases with increasing volume concentration, this trend is observed also in Figure 9. Where, the volume fraction of graphene nanosheets increases the distance between graphene nanosheets decreases in water. Due to, the carbon-carbon interaction increases and the potential energy increases, which is confirmed in Figure 13, showing the variation of potential energy of aqueous nanofluid containing graphene nanosheets. It is observed that the potential energy increased with increasing the volume fraction of graphene nanosheets. The approach Green-Kubo theory relates the microscopic heat flux autocorrelation function $\langle \overrightarrow{j}\left(t\right).\overrightarrow{j}\left(0\right)\rangle$ to the thermal conductivity equation (4). Consequently, the increasing potential energy leads to increasing the heat flux JP according the equation (10). Next, it leads to increasing the microscopic heat flux equation (8), therefore based on equation (4), the thermal conductivity of nanofluid increases with the increasing the volume fraction of graphene nanosheets. Also, this result is explained in our previous study.²³ In which the influence of solid–solid inter-atomic potential type on thermal conductivity of nanofluids is analyse by MD simulations. It is found that the thermal conductivity enhancement of (Ar–Cu) nanofluid increases with increasing the interaction potential in nanoparticles.

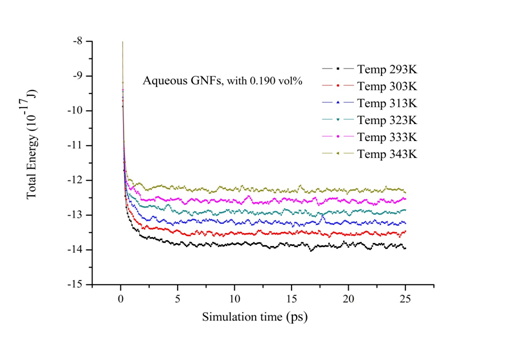
Figure 7 The evolution of internal energy of aqueous GNFs (concentration 0.190%) during MD simulation.

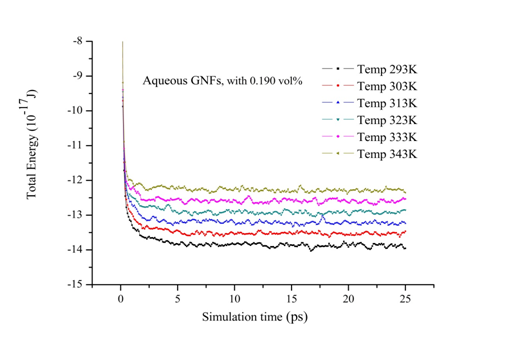
Figure 8 Comparisons between the thermal conductivities of aqueous GNFs (concentration 0.190%) calculated by simulation MD, and that measured by Xing Li et al.⁴⁵

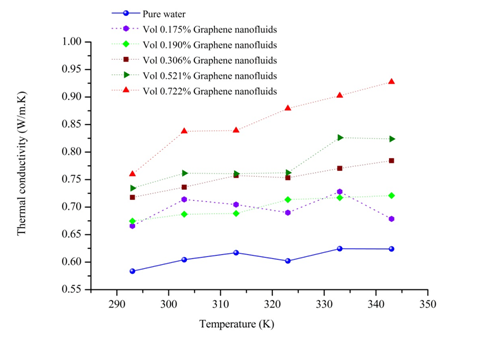
Figure 9 Thermal conductivity of aqueous graphene nanosheet as a function of temperature for various concentrations.

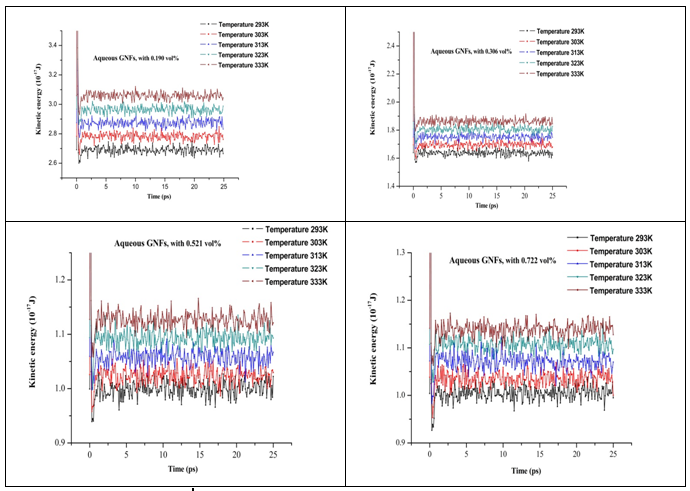
Figure 10 Kinetic energy of aqueous graphene nanosheet for various volume fractions (0.190%, 0.306%, 0.521%, and 0.722%) at different temperatures.

Figure 11 Comparison of numerical values of thermal conductivity of aqueous GNFs with that predicted by Maxwell’s model at different concentrations: 0.190%, 0.306%, 0.521%, and 0.722%.

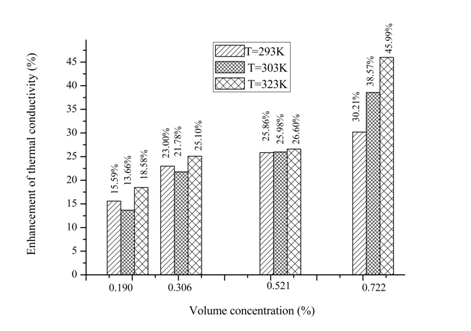
Figure 12 Variation in percentage enhancement of thermal conductivity of graphene–water nanofluid as a function of volume concentration at different temperature (293, 303 and 323K).

Figure 13 Potential energy of aqueous graphene nanosheet at different temperatures (293, 303, 313, 323 and 333K) for various volume fractions (0.175%, 0.190%, 0.306% and 0.521%).

In summary, the molecular dynamics simulations combined with Green-Kubo formula is employed to calculate the thermal conductivity of aqueous GNFs and to investigate the effects of temperature and volume fraction on thermal conductivity enhancement of aqueous GNFs. The SPC/E (extended simple point charge) water model was used to describe water molecules interactions and the interactions for water molecules have been treated as a combination of Lennard-Jones (L-J) interactions and a coulomb term for electrostatic interactions, and the Lennard-Jones (L-J) potential is used to model the interactions between graphene atoms. The molecular dynamic tool is validated by comparing the thermal conductivity of pure water and aqueous GNFs (volume fraction 0.190%) with the previous experimental studies. The effect of temperature is studied by analysing the temperature reliance of the kinetic energy and the microscopic heat flux. Furthermore, the effect of volume fraction is studied by analysing the volume fraction reliance of the potential energy and the microscopic heat flux. It has been found that increasing volume concentration of graphene nanosheets in pure water increases the thermal conductivity enhancement of aqueous GNFs. As well as, the increasing system temperature enhances thermal conductivity enhancement significantly.

None.

Author declares there is no conflict of interest.

1. Choi SUS. Enhancing thermal conductivity of fluids with nanoparticles. ASME–Publications–Fed. 1995;231:99.
2. Sarafraz MM, Hormozi F, Comparatively experimental study on the boiling thermal performance of metal oxide and multi–walled carbon nanotube nanofluids. Powder Technol. 2016;287:412–430.
3. Sheikholeslami M, Ganji DD. Heat transfer of Cu–water nanofluid flow between parallel plates. Powder Technol. 2013;235:873–879.
4. Sheikholeslami M, Bhatti MM, Active method for nanofluid heat transfer enhancement by means of EHD. Int J Heat Mass Transfe. 2017;109:115–122.
5. Masuda H, Ebata A, Teramae K, et al. Alteration of Thermal Conductivity and Viscosity of Liquid by Dispersing Ultra–Fine Particles (Dispersion of y–A12O3 , SiO2 , and TiO2 Ultra–Fine Particles). Netsu Bussei (Japan). 1993;7(4):227–233.
6. Choi SUS, Zhang ZG, Yu W, et al. Anomalous thermal conductivity enhancement in nanotube suspensions. Appl Phys Lett. 2001;79:2252–2254.
7. Ding Y, Alias H, Wen D, et al. Heat transfer of aqueous suspensions of carbon nanotubes (CNT nanofluids). Int J Heat Mass Transfer. 2006;49(1–2):240–250.
8. Xie H, Lee H, Youn W, et al. Nanofluids containing multiwalled carbon nanotubes and their enhanced thermal conductivities. Appl Phys Lett. 2003;94:4967–4971.
9. Ahammed N, Asirvatham LG, Titus J, et al. Measurement of thermal conductivity of graphene–water nanofluid at below and above ambient temperatures. Int Commun Heat Mass Transfer. 2016;70:66–74.
10. Selvam C, Lal DM, Harish S, Thermal conductivity enhancement of ethylene glycol and water with graphene nanoplatelets. Thermochim Acta. 2016;642:32–38.
11. Akhavan–Zanjani H, Saffar–Avval M, Mansourkiaei M, et al. Turbulent convective heat transfer and pressure drop of graphene–water nanofluid flowing inside a horizontal circular tube. J Dispersion Sci Technol. 2014;35(9):1230–1240.
12. Yu W, Choi SUS, The role of interfacial layers in the enhanced thermal conductivity of nanofluids: a renovated Maxwell model. J Nanoparticle Res. 2003;5(1–2):167–171.
13. Leong KC, Yang C, Murshed SMS, A model for the thermal conductivity of nanofluids–the effect of interfacial layer. J Nanoparticle Res. 2006;8(2):245–254.
14. Keblinski P, Phillpot SR, Choi SUS, et al. Mechanisms of heat flow in suspensions of nano–sized particles (nanofluids). Int J Heat Mass Transfer. 2002;45(4):855–863.
15. Xue L, Keblinski P, Phillpot SR, et al. Effect of liquid layering at the liquid–solid interface on thermal transport. Int J Heat Mass Transfer. 2004;47(19–20):4277–4284.
16. Chon CH, Kihm KD. Thermal conductivity enhancement of nano fluids by Brownian motion. Int J Heat Mass Transfer. 2005;127(8):810.
17. Timofeeva EV, Gavrilov AN, McCloskey JM, et al. Thermal conductivity and particle agglomeration in alumina nanofluids: Experiment and theory. Phys Rev E Stat Nonlin Soft Matter Phys. 2007;76(6 Pt 1):061203.
18. Jesumathy S, Udayakumar M, Suresh S. Experimental study of enhanced heat transfer by addition of CuO nanoparticles. Heat Mass Transfer. 2012;48:965–978.
19. Nguyen CT, Desgranges F, Galanis N, et al. Viscosity data for Al2O3–water nanofluid—hysteresis: is heat transfer enhancement using nanofluids reliable? Int J Therm Sci. 2008;47(2):103–111.
20. Zhao C, Chen YK, Jiao Y, et al. The preparation and tribological properties of surface modified zinc borate ultrafine powder as a lubricant additive in liquid paraffin. Tribol Int. 2014;70:155–164.
21. Battez AH, González R, Viesca JL, et al. CuO, ZrO 2 and ZnO nanoparticles as antiwear additive in oil lubricants. Wear. 2008;265(3‒4):422–428.
22. Sorooshian A, Ashwani R, Choi HK, et al. Mater Res Soc Symp Proc. 2004;816:125.
23. Loulijat H, Zerradi H, et al. Effect of Morse potential as model of solid–solid inter–atomic interaction on the thermal conductivity of nanofluids. Adv Powder Technol. 2015;26(1):180–187.
24. Eapen J, Li J, Yip S. Mechanism of thermal transport in dilute nanocolloids. Phys Rev Lett. 2007;98(2):028302.
25. Cao BY, Dong RY. Molecular dynamics calculation of rotational diffusion coefficient of a carbon nanotube in fluid. J. Chem. Phys. 2014;140(3):034703.
26. Allen M, Tildesley DJ. Computer Simulations of Liquids. Oxford: Clarendon Press; 1987.
27. Saito R, Matsuo R, Kimura T, et al. Anomalous potential barrier of double–wall carbon nanotube. Chem Phys Lett. 2001;348:187–193.
28. HJC Berendsen, JR Grigera, TP Straatsma. The missing term in effective pair potentials. J Phys Chem. 1987;91(24):6269–6271.
29. Zhang Y, Zhu Y, Li Z, et al. Temperature–dependent structural properties of water molecules confined in TiO2 nanoslits: Insights from molecular dynamics simulations. Fluid Phase Equilib. 2016;430:169–177.
30. Bandura AV, Kubicki JD. Derivation of force field parameters for TiO2− H2O systems from ab initio calculations. J Phys Chem B. 2003;107(40):11072–11081.
31. Okeke G, Hammond RB, Antony SJ. Effects of heat treatment on the atomic structure and surface energy of rutile and anatase TiO 2 nanoparticles under vacuum and water environments. Chem Eng Sci. 2016;146:144–158.
32. Ryckaert JP, Ciccotti G, Berendsen HJ. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n–alkanes. J Comput Phys. 1977;23:327–341.
33. Cygan RT, Liang JJ, Kalinichev AG. Molecular models of hydroxide, oxyhydroxide, and clay phases and the development of a general force field. J Phys Chem B. 2004;108(4):1255–1266.
34. Keblinski P. Mechanisms of heat flow in suspensions of nano–sized particles (nanofluids). Int J Heat Mass Transfer. 2002;45(4):855–863.
35. Cui W, Shen Z, Yang J, et al. Influence of nanoparticle properties on the thermal conductivity of nanofluids by molecular dynamics simulation. RSC Advances. 2014;4:55580‒55589.
36. McQuarrie DA. Statistical Mechanics. Sausalito: University Science Books; 2000. 520 p.
37. Sarkar S, Selvam RP. Molecular dynamics simulation of effective thermal conductivity and study of enhanced thermal transport mechanism in nanofluids. J Appl Phys. 2007;102(7):074302.
38. Vogelsang R, Hoheisel C. Thermal conductivity of a binary–liquid mixture studied by molecular dynamics with use of Lennard–Jones potentials. Phys Rev A. 1987;35:3487.
39. Plimpton S. Fast parallel algorithms for short–range molecular dynamics. J Comput Phys. 1995;117(1):1‒19.
40. Stukowski A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Modell Simul Mater Sci Eng. 2009;18(1):015012.
41. Humphrey W, Dalke A, Schulten K. VMD: visual molecular dynamics. J Mol Graph. 1996;14(1):33–38.
42. Tsai JL, Tu JF. Characterizing mechanical properties of graphite using molecular dynamics simulation. Mater Des. 2010;31(1):194‒199.
43. Jang SP, Choi SU. Role of Brownian motion in the enhanced thermal conductivity of nanofluids. Appl Phys Lett. 2004;84:4316‒4316.
44. Akhavan–Zanjani H, Saffar–Avval M, Mansourkiaei M, et al. Turbulent convective heat transfer and pressure drop of graphene–water nanofluid flowing inside a horizontal circular tube. J Dispersion Sci Technol. 2014;35(9):1230–1240.
45. Li X, Chen Y, Mo S, et al. Effect of surface modification on the stability and thermal conductivity of water–based SiO 2–coated graphene nanofluid. Thermochim Acta. 2014;595(10):6–10.
46. JC Maxwell. On Electricity and Magnetism. 2nd ed. Clarendron, UK: Oxford; 1881.
47. Khadem MH, Wemhoff AP. Molecular dynamics predictions of the influence of graphite stacking arrangement on the thermal conductivity tensor. Chem Phys Lett. 2013;574:78–82.