The real dataset has many shortcomings that pose challenges to machine learning. High dimensional and imbalanced class prevalence is two important challenges. Hence, the classification of data is negatively impacted by imbalanced data, and high dimensional could create suboptimal performance of the classifier. In this paper, we explore and analyse different feature selection methods for a clinical dataset that suffers from high dimensional and imbalance data. The aim of this paper is to investigate the effect of imbalanced data on selecting features by implementing the feature selection methods to select a subset of the original data and then resample the dataset. In addition, we resample the dataset to apply feature selection methods on a balanced class to compare the results with the original data. Random forest and J48 techniques were used to evaluate the efficacy of samples. The experiments confirm that resampling imbalanced class obtains a significant increase in classification performance, for both taxonomy methods Random forest and J48. Furthermore, the biggest measure affected by balanced data is specificity where it is sharply increased for all methods. What is more, the subsets selected from the balanced data just improve the performance for information gain, where it is played down for the performance of others.

Keywords: clinical data, imbalance class, feature selection, oversampling, under-sampling, resampling

PCA, principal component analysis; LDA, linear discriminant analysis; SVM, support vector machine; IR, imbalance ratio; RF, random forest; TN, true negatives; FP, false positive; PPV, positive predicted values

Clinical datasets commonly have an imbalanced class distribution and high dimensional variables. Imbalanced class means that one class is represented by a large number (majority) of samples more than another (minority) one in binary classification.¹ For example, in our research dataset there are 1459 instances classified as “Alive” while 485 are classified as “Dead”. Machine learning is generally predisposed by imbalanced data because most standard algorithms expect balanced class distributions, thereupon learning classification techniques achieve poorly for imbalanced data.^1,2 Many real world applications are critical for imbalanced data learning such as medical diagnosis, pattern recognition, and fraud detection.³ Methods that can used to solve imbalanced data are categorized as the pre-processing approach and the algorithmic approach. The handling obtained by resampling the class distribution is by under-sampling the majority class, or over-sampling the minority class in the training set.^2,4 While boosting is an example of an algorithmic approach that recalculates weights with each iteration to place different weights on the training examples.⁵ High dimensionality is one of the obstacles facing the mining of clinical data because high dimensionality causes high computational costs, difficulties interpreting data and may influence the classification performance. The dimensionality reduction categories have two types; feature extraction and feature selection. Feature extraction transforms the existing features into a lower dimensional space, for example, principal component analysis (PCA) and linear Discriminant analysis (LDA). Feature selection plays a crucial role in machine learning and pattern recognition.⁶ It is generally the main data processing step prior to applying a learning algorithm.⁷ Feature selection leads to reducing computation requirements, reducing the effect of the curse of dimensionality and developing the predictor performance.⁸

Feature selection is an important technique used in pattern analysis; it decreases data dimensionality by eliminating irrelevant and redundant variables. As Poolsawad et al.¹ stated, feature selection attempts to find the best subset of the input feature set, the selected subset must be the most relevant attributes, without transformation variables. The feature selection has three approaches

1. Wrapper methods
2. Filter methods and
3. Embedded methods.

In the filter methods, the evaluation is independent of the classification algorithm, and the objective function evaluates attributes’ subsets by their information content i.e. interclass distance, statistical dependence or information measures. Conversely, the evaluation of wrapper methods uses criteria related to the classification algorithm, where the objective function is a pattern classifier that evaluates the subsets by the predictive accuracy. However, wrapper methods are slow in execution because they must train a classifier for each feature subset. Additionally, the wrappers lack generality since the optimal feature subset will be specific to the classifier under consideration. Embedded methods is a new procedure that tries to combine ranking and wrapper, these methods measure the usefulness of feature subsets by searching among the learning process where it uses cross-validation for assessment. This means that embedded is similar to wrapper with less computationally expense and is less prone to over fitting. In this research, we investigate feature selection issues in the imbalance situation. The paper is structured as follows: section 3.1 discusses the balanced class methods. Section 3.2 discusses the feature selection methods used in this paper. Information about the dataset used, the classification algorithm, and performance measure are discussed in sections 4.1, 4.2, and 4.3 respectively. Section 5 presents and discusses the results obtained by the experiments and section 6 presents the conclusions.

Class imbalance

When processing a large volume of data it is essential to come up with a random sample, smaller in size, which is called sampling.⁹ Random sampling means each instance has an equal chance to be included in the dataset, this could involve with replacement, or without replacement. Sampling with replacement refers to selecting an instance more than once; this is used for the bootstrap algorithm. On the other hand, sampling without replacement for each instance selected simply rejects the second copy. Bootstrap is the mechanism that each time a sample was taken from a dataset to form a test or training set, it was drawn without replacement.⁹

The imbalance ratio (IR) is measured by dividing a number of samples of the minority class by a number of samples of a majority class, as:

$IR= \frac{Number of negative class instances}{Number of positive class instances}$ (1)

Several approaches can be used to solve imbalances class:

Data level: these methods create balanced data from the imbalanced training dataset.¹⁰ Methods in this level are called resampling methods that can be divided into:

1. Resampling (external): Re-sampling is basically a method that can balance the imbalanced class; it provides a convenient and effective way to deal with imbalanced learning problems using standard classifiers because it alters the original training set rather than modifying the learning algorithm.³ Therefore, the following methods can be used:
1. Oversampling: In the training set the technique increases the frequency of the majority class, see Figure 1. The drawback of this method is the result in over fitting of the data due to it making exact copies of the minority class.¹¹ Moreover, the size of the training set rises then increases the time to build a classifier.
2. Under-sampling: In the training set the technique decreases the frequency of the majority class. Under-sampling can remove a lot of informative examples which could be useful in the development of the classifiers.¹²
2. Active learning (internal): improves learner performance by selecting the more valuable sample to learn and leaving the less valuable.¹³
3. Weighting the data space: to avoid costly errors the training set distribution is modified using information concerning misclassification costs.¹⁴

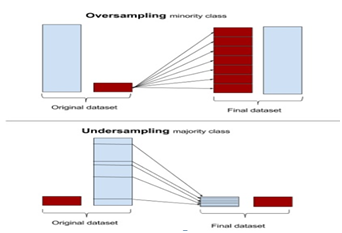
Figure 1 Oversampling increases the minority class by copying instances for minority class. Under-sampling removes instances from the majority class.

Algorithm level (Cost-sensitive learning): by changing the classifier algorithm so it is more precise with the minority class.¹⁰ Cost-sensitive learning attempts to learn more characteristics of minority samples, thus to minimize higher cost errors by considering higher costs for the misclassification of positive class examples with respect to the negative class.^3,14

Methods used in this study to handle imbalance class are:

1. Resample: Produces a random subsample of a dataset using either sampling with replacement or without replacement. The original dataset must fit entirely in memory and the number of instances in the generated dataset may be specified. Using supervised learning, the dataset must have a nominal class attribute. The filter can be made to maintain the class distribution in the subsample, or to bias the class distribution toward a uniform distribution.
2. Spread Subsample: Produces a random subsample of a dataset. The original dataset must fit entirely in memory. This filter allows you to specify the maximum "spread" between the rarest and most common class. For example, you may specify that there must be, at most, a 2:1 difference in class frequencies.

Feature selection

Chi-Squared attribute evaluation: the most simple filter approach is ranking of attributes according to value chi-square for two-way tables; the two-way table for this case is confusion matrix. The method tests the dependence of two variables, therefore does not examine the redundancy between the attributes due to the variables measured individually with respect to the class. It is used to test if the amount of a specific variable and the amount of a specific class are independent. For example, the dataset has features and a target variable, the method calculates chi-squared between every feature and the target and observes the existence of the relationship. Then, if the relation is independent we can exclude this variable. Chi-square is identified by:

${\chi }^2={{\displaystyle \sum }}^{\text{}}\frac{{\left(O-E\right)}^2}{E}$ (2)

Where o is the observed value and e is the expected value, high scores mean that features A and B are dependent. Chi-squared shares similarities with coefficient of determination, R², where R² is applicable only to numeric data. The ranking methods are very simple and the computational time is cheap and equal to $O\left(\log n\right)$ for $n$ features.

Correlation coefficient evaluation: one of the simple methods is Pearson’s Correlation Coefficient which measures a linear correlation between two variables where the resulting value lies between [-1, 1], where -1 refers to a negative relation, 1 refers to positive relation and 0 is no relation between the two variables. The Pearson correlation coefficient is defined as:

$R\left(i\right)= \frac{cov\left(f_i, Y\right)}{\sqrt{var\left(f_i\right)var\left(Y\right)}}$ (3)

Where cov designates the covariance and var the variance, $f_i$ an input feature and $Y$ the output feature. Feature selection technique uses this algorithm to estimate the relationship between each variable and the concept variable, and chooses only the variables that have a high positive or negative relation

ReliefF attribute evaluation: a supervised feature weight estimation, that measures attribute quality to select a feature subset.¹⁵ The idea of a Relief algorithm is it randomly selects features to estimate the feature’s quality that has weights more than the threshold weight using the difference in features value with the nearest sample.¹⁶ By this algorithm, it selects a random instance R, and then searches for K nearest neighbor from the same class (called nearest hit) and each different class (called nearest miss). The formula for updating the weight is as follows:

$W_x=W_x-\frac{diff{\left(F,R,H\right)}^2}{m}+ \frac{diff{\left(F,R,M\right)}^2}{m}$ (4)

Where $W_x$ the weight for is attribute $F$ , $R$ is a random sample instance, $M$ is the nearest miss, $H$ is the nearest hit, $m$ is the number of random sample instances.

Information Gain Attribute Evaluation: it quotes the information between two features using entropy to measure the relevance between the attributes and the concept target, which describes the priority of an inconsistency.¹⁷ It computes the mutual information principle with reference to the number of times: feature value follows a class, the feature value follows without the class, and the class follows without the feature value.¹⁸ We can calculate the information achieved by learning a variable f_i by the information entropy as:

$IG\left(f_i\right)=H\left(T\right)– {{\displaystyle \sum }}^{\text{}}\frac{T_i}{T}H\left(T_i\right)$ (5)

Where $H\left(T\right)$ the entropy of the given dataset is, $H\left(T_i\right)$ is the entropy after the data split using $f_i$ and can calculate as:

$\text{H}\left(\text{T}\right)={\displaystyle \sum }_{c}P\left(c\right)\log \left(P\left(c\right)\right)$ (6)

Wrapper filter: The wrapper uses the induction algorithm itself as part of the evaluation function to search for a good subset.¹⁹ The feature selection algorithm then occurs as a wrapper around the induction algorithm used as a “Black Box”. Black Box is used to prompt a classifier that will be convenient to classify future instances; therefore the algorithm leads to a search for a high-performance subset in terms of classification.²⁰ The evaluation involves the induction algorithm using cross validation to evaluate the precision of the learning scheme for a set of features approximating the accuracy using estimation accuracy techniques. The search space size for n features is $2^n$ with complexity $O\left(n\right)$ due to each state in the search space representing a subset. Wrapper is unfeasible for computationally intensive methods as it must train a classifier for each feature subset²¹

The wrapper can rely on heuristic searching for all possible search subsets, an example of a heuristic search is hill climbing. The hill climbing algorithm shown in Figure 2 displays adding features one at a time until no further improvement can be achieved.

Figure 2 Hill-Climbing Search Algorithm.

Support vector machine (SVM): It is an embedded feature selection which endeavors to select attributes and conclude model parameters instantaneously.²² Embedded methods are different from the Filter and Wrapper methods due to the feature selection performed in the process of learning.²³ The embedded method attempts to find an optimal subset of variables adapting the structure of the classifier, embedded algorithms compromise the interaction with the classification model.TheSVM algorithm uses margin hyper plane to ensure the two patterns are separated linearly; the hyper plane maximizes the sum of distances between the margin and hyper plane.²⁴ The model is trained with all features by setting the coefficients associated with the features to 0 and attempting to remove these features while preserving model performance. If the classes are not linearly then use a variant of SVM.^22,25

Dataset

The dataset used is a real life heart failure dataset obtained from the Hull-LifeLab clinical database (University of Hull, UK). In this dataset, there are 60 features with 1944 patient records, after cleansing data and impute missing values the samples become 1750 instances. The variable 61 is a target output variable that classifies the instances to “Dead” or “Alive”, see Table 1. The imbalance class plain by the percentage of 1 to 3 for Dead to Alive class, and by imbalance ratio which is 33%.

Classification method

C4.5/J48: The j48 technique is an enhancement of the ID3 algorithm,²⁶ the improvement of ID3 are features like speed, size, memory and a rule set output.²⁷ The algorithm steps are:^28–30

1. The tree represents a leaf for the instances existing in the same class, the leaf is returned by labeling with the same class.
2. Calculate the information for each variable, selected by a test on the attributes, and then calculate the achieved information that would be decided from a test on the variable.
3. Iteratively apply the present selection principle to find the highest information gain; this variable is selected for branching.

Random Forest (RF): RF consists of lots of decision trees based on a random selection of data and attributes. The $X_n$ independent variables can be used for building a decision tree, the variables will be selected randomly into sets and these random decision trees create a forest.³¹ The benefit of the large number of trees is that most of the trees can provide correct prediction of class. Another point is that all the trees do not make mistakes in the same place.³² The final classifier gains accurate results since it is taken as a combination of more than one classifier.³³

Performance measures

After the classifiers were trained, the performance of the classifiers is compared using the confusion matrix to find accuracy, sensitivity, and specificity. The confusion matrix is a specific table, where each row represents the instances in a predicted class, with each column representing the instances in an actual class (or vice-versa), as in Table 2.

Where the outcomes are:

True Positive (TP): are the positive elements that classified correctly.

True Negative (TN): are the negative elements that classified correctly.

False Positive (FP): are the negative elements that classified as positive.

False Negative (FN): are the positive elements that classified as negative.

The performance metrics can be measured by different equations such as accuracy, sensitivity, and specificity. Accuracy is simply measured by the possibility that the algorithm can predict negative and positive instances correctly.^34,35 as:

$Accuracy \left(ACC\right)=\frac{TP+TN}{TP+TN+FP+FN}$ (7)

Sensitivity and specificity are the possibility that the algorithms can correctly predict positive and negative instances respectively, as:

$Sensitivity \left(SEN\right)=\frac{TP}{TP+FN}$ (8)

$Specificity \left(SPEC\right)=\frac{TN}{TN+FP}$ (9)

Precession (PPV) measures the proportions of positive and negative results,

$Precision \left(PPV\right)= \frac{TP}{TP+FP}$ (10)

 Five feature selection methods were implemented in this study; they are Chi-squared, information gain, ReliefF, embedded-SVM, and wrapper, to select the best subset of the original dataset that consists of 60 variables. The subsets groups chosen are 11, 23, 34, 44 variables. Then, we find the performance of each one of these groups for each feature selection technique using random forest and J48 methods for classification. After that, we balance the imbalance classes using resample and spread subsample methods and employ random forest and J48 classification again.

Tables 3 illustrate the results of accuracy, specificity, sensitivity, and PPV for a different number of selected features by applying the RF technique. Table 4 shows the outcomes of accuracy, specificity, sensitivity, and PPV for a different number of selected features by applying J48 learning algorithms. From the tables, we notice that chi-squared and wrapper obtained high results when selecting 11 and 23 variables, the performance then decreases when more variables are added. In contrast, information gain starts with an accuracy of 78.87% with 11 features and then increases when more features are added until 86.05% with 44 variables is reached, which is almost equal to other methods. ReliefF and embedded methods starts with 87% accuracy which is a little bit less than the wrapper and chi-squared techniques, then decreases slowly until 85% with 44 variables is reached, which is less than other methods, including information gain. The interpretation for this is that information gain with more variables returns more information improving the gained information which increases the performance. On the other hand, wrapper returns the best results with fewer variables because this method works by repeatedly searching for the best subset that has the best performance with the least features. Further, adopting the embedded SVM technique to pick the features that obtain the best performance with the SVM diagonal, and the observations show that it gets good results with a lower number of attributes, but with an increased number of attributes quantitative the performance is greatly affected. For the research dataset, there are features that can improve the classification performance if they are selected in a subset selection. By measuring the rank correlation between variables rankings, we discern similar techniques that produce the best outcomes. For example, features selected in chi-squared and wrapper mainly appear in both subsets. Similarly, embedded-SVM and ReliefF have many of these features that appear in a selected minimum number of attributes.

As we can see, the accuracy of balanced data using the resample method has significant enhancement since resampling increases the minority class by copying instances called oversampling, or decreases the majority class by deleting instances called under-sampling. Meanwhile, using the spread subsample method does not show significant improvement and almost equal the results with the imbalanced class. We also use a method called Class Balancer that balance classes making the number of each class value equal to another by increasing minority by duplicating their instances and decreasing majority by deleting some of the instances. We did not display the Class Balancer method because it is not a suitable method to balance data and this reduction in classification performance is due to changing the integrity of the dataset, i.e. if the balancing method cannot enhance the classification results we do not need to use it.

The most interesting aspect to note is the specificity results, as we can see it doubled in some cases such as information gain for 11 variables, there was enhancement seen in all other cases for specificity. From equation 9, specificity, also called true negative rate that measures the number of negatives correctly identified. After resampling, the classification of the new dataset has dramatically raised the number of True negatives (TN) and in many cases this has doubled. TN means the true classification of “Dead” instances, where “Dead” value refers to the minority class meaning that resampling can enforce the minority classes by enhancing their samples. On the other hand, equation 9 for the specificity also depends on the false positive (FP) that measure the wrong classification of positive class. In this paper’s dataset, positive referred to the “Alive” class which means the majority class. Therefore, resampling decreases the error of the positives classified. Moreover, the specificity of spread sub-sampling is equal to the specificity of the imbalanced class for all feature selection methods used in this research. The specificity and accuracy with 11 and 23 variables are differentiated depending on the feature selection methods in the two cases of balanced and imbalanced class. But by increasing variables to 34 and 44, the specificity and accuracy become equal for all feature selection methods which is around 79% and 94% for specificity and accuracy, respectively, using RF for classification of the balanced class. The same indication is seen in PPV for both classification methods used, where with 44 features it outperform around 93% for all feature selection methods used. From the sensitivity and PPV for balanced classes employed by RF and J48, respectively, it can be seen that the sensitivity becomes more than 99% with small variations either way to all feature selection methods with a different number of variables. The increase in percentage of sensitivity is because of the growing of quantity of the true positive (TP). TP refers to the majority values correctly classified; the resample method raises the number of these values which increases the value of sensitivity to 99%. While positive predicted values (PPV), are raised in the balanced class in the same way as accuracy with significant aggregate.

We resample the dataset to balance the class then implemented feature selection methods to compare the results with the outcome of the original data. We found that after resampling data the selected subsets were not improved but were cut back in all, except the information gain method which was highly upgraded, especially with fewer numbers of features. Referring to Table 5, chi-squared and wrapper decreased in performance in all subsets selected after balance class, while embedded-SVM and ReliefF dropped sharply in the subset selected with 11 variables. In contrast, information gain dramatically increased in accuracy from 78.97% to 86.90% using balanced class for a subset of 11 attributes. Then with 44 variables, all methods had a lesser performance for balanced data than the original dataset, including information gain. Table 6 shows the same comparison but using J48 classification, there is the same observation with 11 and 23 features. Nevertheless, for subsets with 34 and 44 variables, it changes and shows that the results before and after the resampling are almost the same. The explanation for these observations is that the true positive values (TP) of confusion matrix shows little variation between classification of the balanced and imbalanced class, where the changes come to false classified especially false positive (FP). In our dataset the positive class is the “Alive” value which is the majority, and the negative class is “Dead”, which are the minority. Thereupon, resampling has grown the false positives and declined the true negatives, the reason being the majority class was 1313 for the original dataset and became 1329 for the balanced data which means 16 instances changed from positive to negative classes. Accordingly, the relation between attributes changes the combination of the data.

In this paper, we demonstrated the effectiveness of imbalanced class for the high dimensional dataset, moreover, we discussed this issue concerning the implementation of five different feature selections. The feature selection techniques used were information gain, Chi-squared, ReliefF, embedded-SVM, and wrapper, while the manipulation of imbalanced class was employed by resampling and spread subsample, and the learning test used was the J48 and random forest algorithms. The implementation was a supervised random under-sampling for the majority class. Our findings from this paper are that handling a high dimensional imbalanced dataset is valuable for all feature selection methods that are filtering, wrapper, and embedded, depending on the number of features has been selected. This holds for clinical data classification fields, it seems that imbalanced classes provide samples that are unequal to make overviews about groups of the instances. The outcomes of the experiments show that resampling of the imbalanced class generates a good enhancement in performance results for all measurements such as accuracy, specificity, sensitivity, and PPV. In contrast, using spread sub-samples to balance the class distributions the results were no different when compared with classification for the imbalanced class. Specificity had a dramatic increase using resample methods because it raised the number of negative class (minority class) correctly classified, and reduced the number of positive class (majority class) incorrectly classified. All other performance measures performed better using resample to balance class, although they performed less well compared with specificity measure. Even though sensitivity is high for all feature selection methods it goes up to 99%, there are small variation to this for all feature selection methods in a different number of features. The biggest improvement in performance was for the information gain method, considering the resampling added more information to the features which increased the prediction results. The second analysis of this paper was the feature selection on a balanced dataset; the experiments show that the resampling data has highly improved only the information gain method. All other methods reduced their performance, or produced the same performance as the original data. This is because when information is added the interrelation between attributes and the target class is increased. However, other methods affected by dispersion of the new samples, for example, ReliefF which depends on nearest instances with class’s values, new samples causes mistakes in this relation. For any future work, another technique of balancing class could be performed, and experiments repeated for other datasets.

None.

None.