
Correspondence:
Received: January 01, 1970 | Published: ,
Citation: DOI:
Download PDF
Abstract
Prosthesis is an artificial medical device used to replace a missing human body part. One challenge for such a device, which usually has a structure resembling the missing body part, is how to optimally satisfy the contradictory requirements of dynamic and static stability. In accord with ICM and stability of the natural human knee, we propose a new knee mechanism with an incongruent three-dimensional ICM pathway. This mechanism optimally solves the problem of dynamic and static stability with the use of an elastic joint and deformation contact together with sliding and rolling technologies. This paper describes the schematic design, composition, and component functions of the proposed knee mechanism. From the design and composition of the mechanism, equations are derived for sliding and rolling conditions as prescription criteria, which provide a readily available theory for controlling these motions according to the component functions as well as the motion and definition of the ICM. Moreover, we analyze stability by considering dynamic and static stability under ideal conditions. The results show that the proposed knee mechanism will be promising for next-generation prostheses.
Keywords: knee prosthesis, mechanism design, stability analysis, instantaneous center
Introduction
The natural human knee is the largest and most complicated joint in the human body with incongruent but highly functional particular surfaces. The components of the natural human knee include the femur, tibia, fibula, and patella, as shown in the anatomical diagram of Figure 1(a).1 The principle of knee motion resembles that of a cone wheel sliding and rolling Figure 1(b).2 The instantaneous center is the point where the instantaneous relative velocity is zero on the two members in mutual plane motion. It is also known as a coincident point with identical instantaneous speed. ICM refers to instantaneous centerline (or instantaneous trajectory) of motion. During a pure sliding joint motion, instantaneous center approximates the geometric center coincident with the two bodies, which are infinitesimally far from the joint contact surface, as is shown schematically in Figure 1(c & d).3 On the other hand, during pure rolling, the instantaneous center lies on the joint contact surface. The analysis shows that the ICM pathway of the natural human knee is the 3D and incongruent, which can be describe as a slipping ICM and a rolling ICM. Despite the large forces at the ends of the two longest lever arms in the human body, the knee becomes a fixed straight rod that bears body weight without muscular effort during terminal extension. During flexion and extension of the knee, there is a discrepancy between non-circular leg motions and circular motions of the cruciate ligaments and their insertions. One reason for the excellent function of the knee is that its extension is a combination of rolling and sliding with an incongruent 3D ICM pathway based on deformation contact.4 Walking is a cyclic process in which a sequence of distinct phases is repeated in a continuous fashion. One complete sequence of lower limb motions and position is referred to as a gait cycle, which can be divided into different phases (Figure 2).5 A prosthesis is an artificial medical device used to replace a missing body part, or a novel musculoskeletal humanoid robot with a human-like structure. The most basic function of the prosthesis proposed here is to provide the structural support that would otherwise be provided by the missing or removed portion of the knee. More advanced prostheses include features to provide stability control, physical damping, and energy storage and release—features that partially replace the function of missing or altered musculature.5−7

Figure 1 Kinetic characteristics of natural human knee.
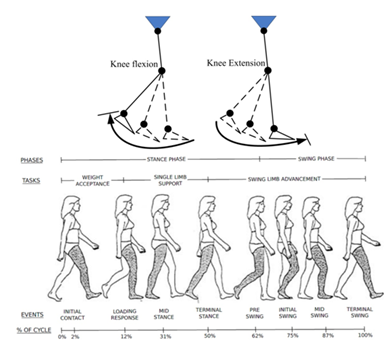
Figure 2 Normal human walking cycle illustrating the events of gait.
Kinematics characteristics of knee mechanism
The knee mechanism is the most important part of the prosthesis. If designed well, it has the potential to provide good knee-stability characteristics in the stance and swing phases.6 For the user’s safety, static knee stability is a main prescription criterion of the prosthesis for bearing weight and not flexing readily in the stance phase. In contrast, dynamic knee stability is the main prescription criterion for the knee to smoothly transition from the stance to swing phase.8 In addition, the ICM, which is described as the coincident point on two bodies with the same velocity, provides valuable information about the kinematic characteristics of the knee mechanism. One way to compare the stability characteristics of knee mechanisms is to visualize the contribution of the residual hip musculature on the amputated side to the stability of the knee during the stance phase of walking by using a knee-stability diagramFigure 3(b).8,9 Like the four-bar knee linkage, the polycentric knee is widely adopted by amputees because the knee flexion angle increases in which the ICM assumes a series of positions (Figure 3).8 The four-bar prosthetic knee with elevated ICM has been available for many years and has the general appearance shown in Figure 3. It typically has a long anterior link and a short posterior link. This class of four-bar linkage knee offers considerable stability at heel contact and is of primary benefit to geriatric or other amputees with limited ability to control stability through active and voluntary control by using residual hip function on the amputated side. In the cross-hatched zone that defines a region for the knee center where hip moment can control knee stability, an elevated and posterior ICM location increases knee stability (Figure 3(a) & 3(b)). The ICM typically traces a path, which progresses forward and downward toward the cosmetic or anatomical knee center, along an extension of the shank. The ICM path is a regular curve in a plane (Figure 3(b)). In the cross-hatched zone, a highly positioned ICM provides good static knee-stability characteristics in stance phase but poor dynamic stability because it cannot be positioned adequately in a lower position instantly to ensure a smooth transition from the stance to swing phase. Conversely, an ICM positioned lower provides good dynamic knee stability, which enables the knee to smoothly transition from the stance to swing phase, but poor static stability, which may make bearing weight and standing difficult by causing the knee to flex readily. The problems of static and dynamic knee-stability are similar for polycentric knees, such as the single-axis and multiple-bar prostheses.8−10
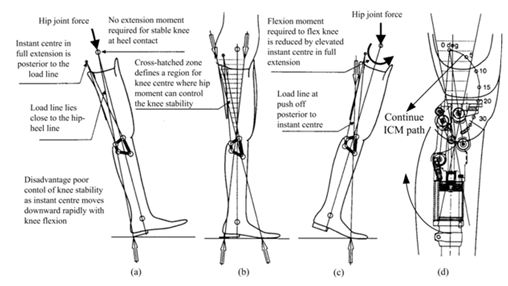
Figure 3 Stability diagram of four-bar knee with elevated ICM.
To allow good cosmetics in sitting, an elevated ICM must rapidly move downward with knee flexion. This sudden shift of the ICM does not allow the amputee to maintain control of the weight-bearing knee if the knee flexes a few degrees as a result of some unforeseen event. However, a knee mechanism with an elevated and posterior ICM during full extension will essentially be locked in extension at heel contact. At the end of the stance phase, the amputee typically initiates knee flexion by initiating swing-through from the hip after lifting the prosthesis from contact with the walking surface.11 Similarly, six-bar knees (the total knee) can offer a higher level of stance-phase control by adding two additional linkages. The mechanism works like a four-bar knee but also gives the user the ability to set the knee into a positively locked state, simulating the stability at initial contact of a mechanically locked knee. Thus, the six-bar knee combines the stability of the four-bar knee and the control of the voluntarily controlled knee at the terminal stance phase.12,13
Design methods
The ICM pathway provides valuable information about the kinematic characteristics of a knee. That is, a well-designed prosthesis reproduces the design of the ICM pathway for the knee mechanism; the more similar the ICM pathway to that of the natural knee, the better the bionic performance of the prosthesis. The natural human knee, just like any other biological structure, is the product of natural evolution. A well-designed human knee mechanism may draw inspiration from the biological design features of the natural knee. Ideally, if a simulated knee mechanism with an incongruent 3D ICM pathway (i.e., where the position of the ICM is high in the stance phase and is immediately lowered upon a shift to the swing phase) were invented, the contradictory requirement of dynamic and static stability could be satisfied for the prosthesis.
Configuration of the novel mechanism
In accord with the biological features and ICM of the natural human knee, a new bio-mechanism is designed to enhance the dynamic and static stability of the prosthesis. Schematic diagrams of the design are shown in Figure 4. Perspective views of the 3D schematic diagram are also shown in Figure 5. Figure 4(b) shows the sliding and rolling mechanism of the simulated knee. The upper part (part 1), rotating part (part 2), tibia part (part 3), rotating shaft (part 4), ball bush (part 5), bumper block (part 6), spring (part 7), ball linkage (part 8), return-spring (part 9), and nether part (part 10) constitute an automatic stance-phase lock prosthetic knee joint, which employs an anterior lock to automatically engage and disengage in response to loading of the prosthesis. In the stance phase, part 8 is locked; this limits the rotation of part 2. At the same time, part 1 is limited by the groove and part 2 (Figure 4(b) & Figure 4(c)). Parts 1 and 3 are always in contact under the piston mechanism with the preload spring, and can slide and roll in the process of flexion and extension. Ideally, parts 1 and 2 make up a revolute joint, parts 2 and 8 make up the shifting pair, and parts 8 and 5 act as a spherical joint. Parts 4 and 10 make up the revolute joint. Under the preload force of part 7, parts 1 and 3 remain in contact to make up a higher planar pair (only in the stance phase; Figure 3(b) & Figure 3(c)).
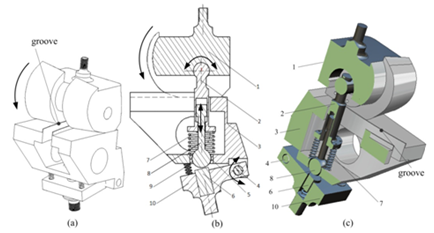
Figure 4 Assembly drawing and schematic diagram of the simulated knee mechanism.
Functions of key components of the novel mechanism
Preload spring (part 7): Inspired by the connections of ligaments and muscles in human knee joints, a spring connection design was made to mimic the human connections to achieve a three-dimensional instantaneous centerline closer to the natural human knee joint. This novel knee prosthesis mechanism works like a four-bar knee but also gives the user the ability to set the knee into a positively locked state, simulating the stability at initial contact of a mechanically locked knee. Parts 1 and 3 are jointed by the piston mechanism with the preload spring (Figure 4(b) & 5(e)). The preload spring maybe has the little effect to change ICM pathway, but is the key to make Parts 1 and 3 are always contenting like the nature human knee with the spring buffer. As such, this part is necessary. The ICM pathways are greatly affected by the preload force, which should be accordingly varied when rolling and sliding motions happens. If the change in the preload force approximates the force exerted on the muscles and ligaments when the natural human knee joint moves, a natural joint with good bionic effect can be obtained.
Surface friction coefficient: Depending on the rolling friction, many different surface friction coefficient zones are set for the control of sliding and rolling (Figure 5(b)). Figure 5(c) & 5(d) show schematic diagrams of these zones in part 3. Under different surface friction coefficients, parts 1 and 3 are always in contact to make up a higher planar pair that can slide and roll in the swing phase (flexion and extension). When the contact surface friction coefficient is high, parts 1 and 3 roll easily; when it is low, parts 1 and 3 slides readily. Consequently, a low ICM position for the prosthesis to smoothly transition from the stance to swing phase is obtained by setting the contact zone of the surface friction properties to facilitate sliding. Conversely, a high ICM position for the prosthesis to achieve dynamic knee stability in the stance phase is obtained by setting the contact zone of surface friction properties to facilitate rolling. In this way, the ICM pathway may theoretically be rendered discontinuous, which optimally satisfies the contradictory requirements of dynamic and static stability. Deformation contact may be beneficial for the knee mechanism to prevent surface abrasion. This could improve the function of humanoid prostheses.

Figure 5 Schematic of incongruent 3D ICM control.
Surface shape: Part 1 is biomimetically designed in the shape of the femur. Its motion is limited by its outer contour, which is defined by the groove and cone (Figure 5(f)). Part 1 can roll and slide around the circular center O with the groove, which brings the ICM closer to the natural knee based on the preload spring and surface friction properties. Theoretically, the groove can create an ICM plane; after adding the cone, the motion and ICM pathway lies on three planes. Figure 5(a) & 6 show the schematic. Figure 6 (a-c) displays the 3D printing model of the simulated knee. The parameters of the cone and groove (Figure 6(d)), like the depth and conical degree, can be estimated from the gait, ICM, and characteristics of the natural human knee.

Figure 6 Limit of the groove and side tumbling test.
Motion analysis of the novel mechanism
The ICM is described as the coincident point on two bodies with the same velocity. Therefore, the ICM pathway is extremely sensitive to the surface shapes of the two bodies, a deformable or rigid contact, and the motion of sliding and rolling.3,14 Parameters that affect the motions (parts 1 and 3) of sliding and rolling are the preload spring, surface shape, rolling friction coefficient, the groove, and cone. Consequently, the parameters that specify these parts greatly affect the ICM pathway. To describe the motion, we used the motion test shown in Figure 6 to mathematically analyze the contribution of the parameter of a specific part to the ICM position by assuming that part 3 is static. The simplified analysis is schematically shown in Figure 7(b & c). The 3D motion can be simplified by assuming it to be planar, because two-dimensional analysis is a popular and useful technique when studying the complex simulated biomechanics of a knee mechanism.14−16 The schematic is established according to the definitions of sliding and rolling (Figure 7). Figure 7(c & d) schematically show a simplified analysis of the stance phase depicted in Figure 7(a), whereas Figure 7(b) shows the swing phase after a flexion of θ with flexion moment M1, where the contact point is A and B shifts to B1. The preload force is the main factor that ensures parts 1 and 3 are always in contact; the vertical preload force must satisfy if we wish to make a simulated knee prosthesis available. Assuming that the quality of the simulated knee prosthesis is m, the quality of part 1 is zero.
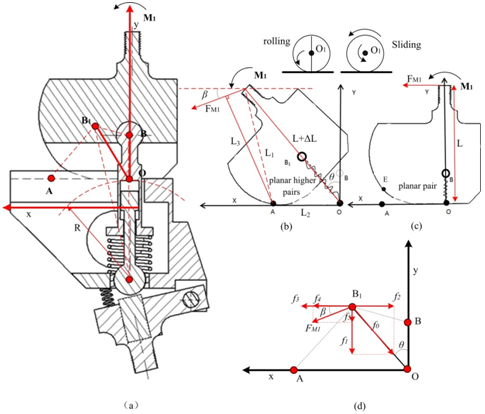
Figure 7 Simplified analysis of simulated knee-mechanism motion.
Assuming the spring preload force is
(1)
Figure 7(d) schematically shows the load analysis of B1. Assuming that the friction of parts 1 and 3 is f3, the tension of the spring (part 7) is f0, which can be divided into f1 and f2. FM1 can also be divided into f4 and f5.
(2)
(3)
(4)
(5)
(6)
(7)
(8)
Equations (3) and (8) lead to
(9)
Equations (4) and (6) lead to
(10)
Where
m is the quality of the simulated knee mechanism, assuming that the quality of part 1 is zero.
K1 is the damping coefficient.
g is the acceleration of gravity.
µ is the surface friction coefficient.
θ is the rotation angle of part 1.
L is the distance from the force-bearing point to the surface contact point of the planar pair in the stance phase.
L1 is the distance from the force-bearing point to the surface contact point of the higher planar pairs in the swing phase.
L2 is the distance from the contact point to origin O.
L3 is the moment arm.
M1 is the moment.
β is the rotation angle of FM1.
According to the definitions of rolling and sliding, when the motion is rolling, and when the motion is sliding. Assuming that the ICM parameter equation is
(11)
Equations (2), (10), and (11) then lead to
(12)
Equations (9) and (12) lead to the ICM parameter equation
(13)
Theoretically, the ICM pathway is extremely sensitive to sliding and rolling motions. The ICM parameter equation illustrates the impact of the parameters for the parts on the motion and ICM pathway. Equation 13 shows that the motion and ICM position are sensitive to the surface parameters of part 1, i.e., the spring and surface friction coefficient. Ideally, the ICM pathway can be designed on the basis of the ICM parameter equation f (Ψ). If we wish to move the ICM distant from the contact surface, we can facilitate sliding by setting the ICM parameter equation (Figure 8(a)). Conversely, if we wish to move the ICM near the contact surface, we can facilitate rolling by setting the ICM parameter equation(Figure 8(c)).15

Figure 8 The ICM for various types of the part 1.
Analysis of the designed ICM
The study of the intelligent prostheses showed that the user's balance depended on the gait phase when the intelligent prostheses errors happened.16−18 Theoretically, the well-designed slipping ICM and rolling ICM can be making. The regular of the ICM can be designed by changing the parameters of part 1, as show in Figure 5(b) & Figure 6(d). The ICM for the slipping and rolling when part 1 is respectively a cylinder, a cone or a complex cone are shown in Figure 8. Equations (14)-(19) are here introduced to indicate the control regulation of the bionic joints. When the part 1 is a cylinder, as show in Figure 8(b), a straight line ICM for the slipping can be derived and expressed as
(14)
And the regular ICM for the rolling can be expressed as
In the case of, a=3.5, b=4.5, c=3 and d=0 as shown in Figure 8(a), Equations (14) and (15) can be rewritten as, respectively
(14a)
(15a)
When the part 1 is a regular cone, as show in Fig. 8(b), a 2D ICM equation for the slipping can be derived and expressed as
(16)
And the regular ICM for the rolling can be expressed as
(17)
In the case of , a=b=d=e=3, c=3.5 and f=0, as shown in Figure 8(b), Equations (16) and (17) can be rewritten as, respectively
(16a)
(17a)
When part 1 is a complex cone, as show in Figure 8(c), a 3D ICM equation for the slipping can be derived and expressed as
(18)
And the regular ICM for the rolling can be expressed as
(19)
In the case of , a=b=c=d=3, e=0 and, Equations (18) and (19) can be rewritten as, respectively
(18a)
(19a)
Stability analysis of the novel mechanism
The knee-stability characteristics are extremely sensitive to the position of the ICM. Therefore, we need to analyze stability by considering dynamic and static stability. Figure 8 shows the stability diagram of this new knee-mechanism simulated with an incongruent 3D ICM based on the artificial knee prosthesis 5, 8, and 14. Theoretically, if the simulated knee mechanism is sliding, the ICM is infinitesimally far from the joint contact surface (Figure 8(a & b)). If the knee mechanism is rolling, the ICM lies on the joint contact surface (Figure 8(c)). Thus, the new simulated knee mechanism with incongruent 3D ICM can optimally satisfy the contradictory requirements of dynamic and static stability (Figure 8(d)).5 Whereas the ICM can be positioned higher in the stance phase (Figure 8(a & b)), it can be positioned lower instantly upon a shift to the swing phase because the miniature sliding and rolling motions assist the smooth transition from the stance to swing phase (Figure 8(c)). Increasing the ankle angle θ to avoid contact between the ankle and ground (h1>h2; Figure 9) ensures a natural gait and improves safety for the prosthesis user (Figure 10).

Figure 9 Stability diagram of the simulated knee mechanism.
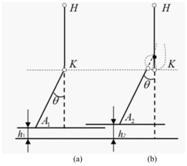
Figure 10 Effect of increasing the ankle angle.
Results and conclusions
In this study, a new method for a simulated knee mechanism was investigated. A promising incongruent 3D ICM pathway was designed for the simulated knee mechanism. This mechanism provided an incongruent ICM (i.e., the ICM could be positioned higher in the stance phase and lowered immediately upon shifting to the swing phase) that could optimally satisfy the contradictory requirements of dynamic and static stability. The mechanism provides a promising approach for developing prostheses with the potential to restore comfort, gait symmetry, and a natural walking gait. Theoretically, the ICM pathway was extremely sensitive to the surface shape of two bodies (parts 1 and 3) and the motions of sliding and rolling. The contacting conditions for the spring (part 7) were defined to make the preload force. Furthermore, the sliding and rolling conditions were deduced according to a preliminary study of the contacting parameter equation and the ICM parameter equation was calculated. The ICM could be optimally obtained from the contacting parameter and the ICM control equations. This design used a theory of deformation contact despite the paucity of biological research on the theory, especially for the human knee. Deformation contact in the human knee may be the key to further research that explores the mysteries of nature’s exquisitely adaptive functions. The present results are only the first step toward a promising prosthesis. The 3D ICM Equation (18) of the slipping and the regular ICM Equation (19) of the rolling should be derived. The challenges for the future will be to identify the precise rules by which the parameters of the preload spring, surface friction coefficient, and shape of the groove and cone for part 1 influence the ICM. Another major challenge will be to identify the material for deformation contact. If established to a practical level, the proposed high-resolution technique will become an essential method for next-generation prostheses.
Acknowledgements
The authors gratefully acknowledge the support of the National Science Foundation of China (2012BAH32F07), Guangxi Natural Science Foundation (grant number 2017GXNSFAA198133), and Guangxi Key Laboratory of Manufacturing System & Advanced Manufacturing Technology (grant number 14-045-15-005Z).
Conflict of interest
The authors declare no conflict of interest.
References
- Biscević M, Tomić D, Starc V, Smrke D. Smrke, Gender differences in knee kinematics and its possible consequences. Croat Med J. 2005;46(2):253−260.
- Iwaki H, Pinskerova V, Freeman MA. Tibiofemoral movement 1: the shapes and relative movements of the femur and tibia in the unloaded cadaver knee. J Bone Joint Surg Br. 2000;82(8):1189−1195.
- Bryant JT, Wevers HW, Lowe PJ. Methods of data smoothing for instantaneous centre of rotation measurements. Med Biol Eng Comput. 1984;22(6):597−602.
- Jampala S Harsha. Evaluation of knee joint stresses during kneeling work. The University of Utah; USA. 2011.
- Dominik W. Evaluation and design of a globally applicable rear-locking prosthetic knee mechanism. Master Thesis, University of Toronto; Canada. 2012.
- Howard B, Yangmanssour JH. A pneumatic human inspired bobotic leg: control architecture and kinematical overview. International Journal of Humanoid Robotics. 2012;9(3):24−29.
- Sakamoto H, Katayose H, Miyazaki K. Extended-knee walk for humanoid robot with parallel link legs. International Journal of Humanoid Robotics. 2009;6(4):565−562.
- Radcliffe CW. Four-bar linkage prosthetic knee mechanisms: kinematics, alignment and prescription criteria. Prosthetics and Orthotics Int. 1994;18(3):159−173.
- Zhang PY, Jin DW, Huang CH, et al. Study on stability and kinematic function of above knee prostheses. Journal of Tsinghua University (Sci &Tech). 1998;38(8):1−4.
- Andrysek J, Naumann S, Cleghorn WL. Design and quantitative evaluation of a stance-phase controlled prosthetic knee joint for children. IEEE Trans Neural Syst Rehabil Eng. 2005;13(4):437−443.
- Gard AS, Dudley S, Childress, et al. The influence of four-bar linkage knees on prosthetic swing-phase floor clearance. Prosthet Orthot Int.1996;8(2):34−40.
- Jin D, Zhang R, Dimo HO, et al. Kinematic and dynamic performance of prosthetic knee joint using six-bar mechanism. J Rehabil Res Dev. 2003;40(1):39−48.
- Chakraborty JK, Patil KM. A new modular six-bar linkage trans-femoral prosthesis for walking and squatting. Prosthet Orthot Int. 1994;18(2):98−108.
- Xu M, Shen LX, Zhao GP. Kinematic analysis of simulated knee prosthesis. Chin Med J (Engl). 2009;39(13):7777−7779.
- Montgomery SC, Moorehead JD, Davidson JS, et al. A new technique for measuring the rotational axis pathway of a moving knee. The Knee. 1998;5(4):289−295.
- Moeinzadeh MH, Engin AE, Akkas N. Two-dimensional dynamic modelling of human knee joint. J Biomech. 1983;16(4):253−264.
- Zhang F, Liu M, Huang H. Effects of locomotion mod recognition errors on volitional control of powered above knee prostheses. IEEE Trans Neural Syst Rehabil Eng. 2015;23(1):64−72.
- Li Rui, Zhang Xiaodong, Liu Chang. Research on human-machine coordinated control method for brain-controlled intelligen prosthesis. Machinery & Electronics. 2017;35(1):63−68.

© . This is an open access article distributed under the terms of the,
which
permits unrestricted use, distribution, and build upon your work non-commercially.


