Samples were collected from the surface type section of the Shajara reservoirs of the Permo-carboniferous shajara formation at latitude 26° 52′ 17.4″ , longitude 43° 36′ 18″. Porosity was measured and permeability was derived from the measured capillary pressure data
The resistivity can be scaled as
………… (1)
Where Sw is the water saturation, Ω = resistivity in ohm meter.
Ω max = maximum resistivity in ohm meter.
Df = fractal dimension.
Equation 1 can be proofed from
……….. (2)
Where k = permeability in millidarcy (md).
1/120 is a constant
F= formation electrical resistivity factor in zero dimension
σ = quadrature conductivity in Siemens / meter
But……….. (3)
Insert equation 3 into equation 2
………… (4)
……. (5)
r in equation 5 is the pore throat radius. Equation 5 after rearrange will become
……….. (6)
Equation 6 after simplification will result in
………… (7)
Take the square root of both sides of Equation 7
…………… (8)
Equation 8 after simplification will become
……………. (9)
The pore throat radius r can be scaled as
……….. (10)
Where v is the cumulative pore volume. differentiate equation 10 with respect to r
…………. (11)
Integrate equation 11
………… (12)
………… (13)
The total pre volume can be integrated as follows:
………… (14)
The result of total pore volume integral
…………. (15)
Divide equation 13 by equation 15
……………. (16)
Equation 16 after simplification will become
……………….. (17)
Insert equation 9 into equation 17
………….. (18)
Equation 18 after simplification will become
……………… (19)
Equation 19 is the proof of equation 1
The geometric relaxation time of induced polarization can be scaled as
…………… (20)
Where Sw = water saturation
IPTg = geometric relaxation time of induced polarization in milliseconds.
IPTgmax = maximum geometric relaxation time of induced polarization in milliseconds.
Df = fractal dimension.
Equation 20 can be proofed from
……………. (21)
k= permeability in millidarcy
9.6 = constant.
Φ = porosity.
1.57 = constant.
The maximum permeability can be scaled as
…………….. (22)
Divide equation 21 by equation 22
……………… (23)
Equation 23 after simplification will become
…………. (24)
Take the square root of equation 24
…………….. (25)
Equation 25 can also be written as
…………… (26)
Take the Logarithm of equation 26
……………. (27)
But
………………. (28)
Insert equation 28 into equation 27
………. (29)
If we remove the Log from equation 29
……………. (30)
Equation 30 the proof of equation 20 which relates the water saturation, the geometric relaxation time of induced polarization, the maximum geometric relaxation time of induced polarization, and the fractal dimension
Petrophysical data characterizing Shajara reservoirs of the permo-Carboniferous Shajara Formation were presented in Table 1. These sandstone reservoirs were divided into three bodies, from bottom to top are: lower, middle, and upper shajara reservoir. Concerning the lower shajara reservoir, it is domenstrated by four sandstone samples named as SJ1, SJ2, SJ3, and SJ4. Their results of resistivity and geometric relaxation time fractal dimensions were displayed in Table 1. Sample SJ1 with a porosity value of about 29% and permeability equal to 1680 millidarcy, whose resistivity and geometric relaxation time fractal dimensions was found to be 2.7859 as revealed in table 1. Sample SJ2 is defined by 35% porosity and permeability around 1955 millidarcy. Its resistivity and geometric relaxation time fractal dimensions of induced polarization equal 2.7748. As we progress from sample SJ2 to sample SJ3 an extreme reduction in permeability was encountered from 1955 millidarcy to 56 millidary which accounts for decrease in fractal dimension from 2.7848 to 2.4379 as explained in Table 1. Such drastic chane in permeability and fractal dimension can account for heterogeneity which is an importment parameter in reservoir qulaity assessment. Again an increase in permeability from 56 millidary to 176 millidarcy was reported as we proceed from sample SJ3 to SJ4 as delineated in Table 1. Such increase in permeability gives rise to fractal dimension from 2.4379 to 2.6843 as presented in Table 1.
However the middle Shajara Reservoir is designated by three sample, so called SJ7, SJ8, and SJ9 as shown in Table 1. Their poroperm data were presented in table 1. Their resistivity and geometric relaxation time fractal dimensions were higher than samples SJ3 and SJ4 due to an increase in their permeabilities as displayed in table 1.
The upper shajara reservoir is illustrated by three samples labeled as SJ11, SJ12, and SJ13 as described in Table 1. Their resistivity and geometric relaxation time fractal dimension values are also higher than samples SJ3 and SJ4 owing to an increase in their flow capacity (permeability) as demonstrated in Table 1. Overall aplot of resistivity fractal dimensions versus geometric relaxation time fractal dimension fractal dimensions of induced polarization (Figure 1) delineates three zones of varing petrophysical characteristics. Such discrepancy in fractal dimension can account for heterogeneity whic is a key parameter in reservoir quality assessment.
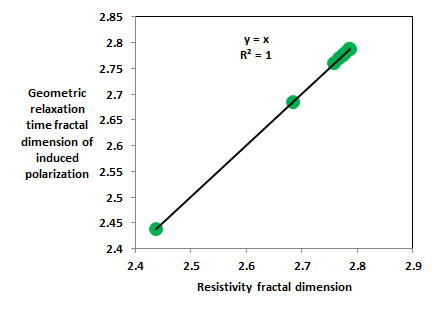
Figure 1 Resistivity fractal dimension versus geometric relaxation time fractal dimension of induced polarization.
Formation |
Reservoirs |
Samples |
porosity |
Permeability |
Resistivity fractal dimension |
Geometric relaxation time fractal dimension |
Permo-Carboniferous
Shajara Formation |
Upper Shajara Reservoir |
SJ13 |
25 |
973 |
2.7872 |
2.7872 |
SJ12 |
28 |
1440 |
2.7859 |
2.7859 |
SJ11 |
36 |
1197 |
2.7586 |
2.7586 |
Middle Shajara Reservoir |
SJ9 |
31 |
1394 |
2.7786 |
2.7786 |
SJ8 |
32 |
1344 |
2.7752 |
2.7752 |
SJ7 |
35 |
1472 |
2.7683 |
2.7683 |
Lower Shajara Reservoir |
SJ4 |
30 |
176 |
2.6843 |
2.6843 |
SJ3 |
34 |
56 |
2.4379 |
2.4379 |
SJ2 |
35 |
1955 |
2.7748 |
2.7748 |
SJ1 |
29 |
1680 |
2.7859 |
2.7859 |
Table 1 Petrophysical model showing the the thee Shajara Reservoirs of the Permo-Carboniferous shajara Formation with their corresponding values of resistivity and geometric relaxation time fractal dimensions of induced polarization
The author would like to thank college of Engineering, King Saud University, Department of Petroleum and Natural Gas Engineering, Department of Chemical Engineeing, Research Centre at college of Engineeing, King Abdullal institute for research and Consulting Studies for their supports



